Асимптотика решений системы сингулярно возмущенных дифференциальных уравнений

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                        

Ранее проводимые работы в этом направлении хорошо изучены. Так, в работах [1, 2, 5, 9–15, 17] рассмотрены случаи, когда собственные значения имели в действительной части значения отличные от нуля, т. е. Л_к ( t ) = а (t ) ± в (t ), k = 1,2 . В этих случаях определены устойчивые и неустойчивые интервалы относительно действительной области. Получены соответствующие оценки.

В предлагаемой работе рассматриваются собственные значения, которые несколько раз меняют условия устойчивости. При этом точки смены устойчивости, начальная и критическая совпадают.

Собственные значения кратные, рассматриваемые задачи нелинейные. В этом случае решение рассматриваемые задач можно оценить и в действительной области, но мы получим решение задачи в комплексной области.

Чтобы не было совпадения точки смены устойчивости, с начальной и критической точками, выбираем начальную точки определенным образом.

Цель исследования. Доказать асимптотическую близость решений возмущенной и невозмущенной задач, когда действительные части собственных значений имеют несколько устойчивых и неустойчивых интервалов. Рассмотрены случаи, при которых точки смены устойчивости, критическая [2] и начальная совпадают.

Материалы и методы исследования

Рассмотрим задачу sy' (t, £) = D (t) y (t, £) + £f (t, y (t, £))                                              (1)

У ⁽ t о , ^£ ) = У °,                                                          ⁽²⁾

где D(t) = diag(Д (t), 22 (t),..., Лк (t)) , среди собственных значений матрицы есть кратные, y(t, £) = colon(yx (t, £), y2 (t, £),..., yk (t, £)) , t gQ ^ C,      0 < £ -малый     параметр, f (t, y(t, £)) = colon(f (t,y), f2 (t,y),..., fk (t, £)), [t0, T) -отрезок       действительной       оси, to < T, (t0 > -T), Q (Q) -пространство аналитических функций, C — комплексная плоскость, k = 1, n .

Пусть выполняются условия:

^ ( t ) g Q ( q ) , V t gQ ( л_к ( t ) ^ 0, k = m J                                     ⁽³⁾

f ( t , y ( t , £ )) g Q ( H ), H = { ( t , y ) t gQ , \y\ < S >  0| },

V у ,y g { y | <  s } ( f ( t , у ) - f ( t , y )| <  M(y - y )), 0 <  M - const                        ⁽⁴⁾

Введем обозначения:

O = { ( t i , 1 2 ) : u k (t i , 1 ₂) - °, k = 1, n }

O = { ( t 1 ,1 ₂ ) : u k (t 1 ,1 ₂) <— £ , k = 1, n }

Q₂ = { ( t i, t ₂) : Uk (^, t ₂) - £ ln £ , k = 1, n }

Q3

= <

⁽ t 1 , t 2 ^): uk ⁽ t 1 , t 2 ) < ^- d ^£ h к

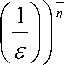
, k = 1, n ,0 <  d <  1, n e N >

04=^ , t ₂): u_k ( t j, t ₂) <- d , k = 1, n ,) 0 <  d <  1 )}                                   ⁽⁹⁾

t где uk(11,12) = Re jAk(s)ds ,(k = 1,n), 11,12 e R, O1 ^^ O2 ^ O^ — ^^ . При этом O ^^ C вся t 0

комплексная плоскость.

Справедлива теорема.

Теорема. Пусть выполняются условия (3), (4). Тогда задача (1), (2) имеет единственное решение и для нее справедлива оценка:

■

|| y(t,£ )|| < Cs(£)

где ^ ( £ ) ^ 0, £ ^ 0 , t e C , C — постоянное число.

Доказательство. От задачи (1), (2) переходим к эквивалентному уравнению:

t y (t, £) = y0 (£))E(t, 10, £) + J E(t, T, £) f (t, y (t, £)dT t 0

t

\

где E ( t , t , £ ) = exp I ¹J D ( s ) ds . к £ T       J

Решение уравнение (11) найдем методом последовательных приближений:

y ⁽⁰⁾( t , £ ) = 0,

y(')1 (t, £) = y ° E (t, 10, £) + jE (t, T, £ ),.f (t, yn -1 (t, £)) dT, t 0

t

где E ( t , 1 ₀,

^£ ) = ^exp _£ J D ⁽ s ) ^ds , ^{n e} N .

к

t

t 0              J

Первообразная функция от собственных значений

t

z ⁽ t , t 0 ) = j A t ^{( s} ) ^ds = u k ( t ) ± i $ k ( t )

t 0

t

t

где u_k ( t, t₀ ) = Re j A_k ( s ) ds , &_k ( t, t₀ ) = Im j \ ( s ) ds , k = 1, n , t ₀, t e C .

t 0

t 0

Линии уровня определяющиеся из (13) являются компенсирующими друг друга. В связи с этим при пограничных слоях можно использовать линии уровня &_k ( t , t₀ ) = - d ,0 <  d <  1, k = 1,2. Если использовать обе линии уровня одновременно, то имеем полное покрытие рассматриваемой области.

~

Определены пути интегрирования l_n , l_n , ( n e N ), n приближения и соединение точки ( t ₀,0 ) с точкой ( t 1 ; 1 ₂ ) . В каждом приближении пути интегрирования l_n = l^J_n , ( j = 1, n ) состоят из отрезков этих путей. Путь интегрирования l_n выбирается симметрично l_n.

Область, определяемая равенством (6) является простирающимися пограничными слоями. Этому дана оценка в работе [14].

Область, определяемая (7) является переходной для пограничных слоев. Это установлено в работе [14].

Область, определяемая (8) является исключаемой регулярной областью, поэтому для получения оценки равенства (12) можно выбирать пути интегрирования.

Область, определяемая (9) является уверенной регулярной областью. В этой области, учитывая равенства (12) также можно выбрать пути интегрирования для получения оценки.

Учитывая пути интегрирования, производим оценку последовательных приближений y ⁽¹⁾ ( t , е ) = у⁰ E ( t , 1 0 , в ) + j E ( t , т , £ ) f ( t ,0) d т . l 1

Оценка задачи (1), (2) оценивается таким образов | y ⁽¹⁾ ( t , £ )|| <  C d ( £ ), где C — некоторая постоянная. Далее учитывая условия (4) имеем

||у(2) (t, £)|| < |у(1) (t, £)| + j E(t, т, £)| X | f (т, у(1) (т, £) - f (т,0)|dT

некоторая постоянная.

Предположив справедливость неравенства

~_...~         ~        ~

||y⁽ \t, £) < C6(£) + (Cd(£)) +... + (C^(£)) , где C — некоторая постоянная, n e N .

Устанавливаем доказательство справедливости оценки (10).

Теперь докажем сходимость последовательных приближений. Имеем

||у⁽¹⁾(t, £)|| < CS(£) < 1 ,||y⁽²⁾(t, £) - у^W(t, £)|| < (C^£))²< 1,

IIу^{(3) (}t,^£)^-у^{(2) (}t,^£)|| < CW)/ < 1 .Предположим, что выполняется неравенство

||у^(n-1)(t, £) - у^(n-2)(t, £)|| <(сд(£))   < 1.      Докажем      справедливость      оценки

||у⁽ⁿ) (t, £) - у^(n-1)(t, £)||. Имеем ||у⁽n) (t, £) - у^(n-1) (t, £)|| < (C$(£))ⁿ< 1.

Построим ряд от

Z(у^(k'(t,£) - у»-⁾(t, £))

k =1

Если ряд (14) сходится равномерно, то последовательность {у⁽ⁿ)(t,£)} сходится равномерно.

Докажем равномерную сходимость ряда. Имеем:

о                             о

Z(yk)(t, £ ) - y < k-\t, 8 )) <3 y < k \t, £ )-y < k-1)(t,£ )| = ||y<"(t, £ )-y «(t, £ )) + k=1                                            k=1

+ |y(2)(t, 8) — y (1)(t, £)| + ... + |y(n\t, 8)- y(n-1) (t, £)|| + ... = CC8(£) + (C8(£))

+

~      П++1

+ CS( +  -C8(^x 1 -(C5(£>)

+... + (C8(£)) +... = C8(£) xl 1 — (c^(£))   .

В рассматриваемой области]y⁽n\t,£)|| < C8(£)x

к

I ~      nn+1 \

-Й >)

1 — C8(£)   I

, и при n ^ о получим

||y(t, £)|| < C8(£) .Теорема доказана.

Пример. Пусть собственные значения матрицы являются кратными комплексносопряженными Л1(t) = ^(t) = t3 -1 + i(2t2 -1) и   A2 (t) = 24 (t) = t3 -1 - i(2t2 -1). Если действительная часть собственных значений отрицательна в интервалах t g (-»;-1)u(0,1) — то это устойчивый интервал, при t g(- 1;0)u(1;+®) — неустойчивый интервал, а t = ±1 — точки перехода от устойчивого к неустойчивому интервалу, t = 0 — точка перехода от неустойчивого к устойчивому интервалу.

Действительная часть характеристической функции равна

t                    ^4     ^2

Re jЛ⁽s)ds "-у t 0

Решая (15) как уравнения, найдем   1₁ =-V 2 ,   t₂= t₃= 0 ,   1₄ = 22 . При

t g (-о;-42)и (42;+о)

— сингулярная область, а при t g

(- V2;0)o(0;V2 )

— регулярная

область. Если за начальную точку возьмем t = -22 , то точка t = 0 одновременно является и точкой смены устойчивости, и начальной и критической. Поэтому начальную точку выберем иначе, с дополнительным условиям.

Результаты и обсуждения

Подведя итог, можем сказать, что последовательность {y⁽ⁿ)(t, £} равномерно сходится к некоторой функции y(t, £) , которая является решением уравнения (1). Надо отметить что, если t g Q₄, то имеем оценку равную 8(£) = £ . Эта область является уверенной регулярной областью. Если t g Q₃, то область является исключаемой регулярной областью и верна оценка (10). В свою очередь при £ ^ 0 , 8(£) — является бесконечно малой величиной, но £ = о (8(£)). Поэтому для разных областей, получаем разные оценки.

В работах [1, 2, 5, 9–15, 17] рассмотрена область, в которой для собственных значений выполняются условия (5), определяемые области совпадают. В данном случае, тоже требуем выполнение условия (5), но они выражают разные области, имеющие общие границы. Это связано с выбором собственных значений. Если потребуем выполнения условия как в работах [1, 2, 5, 9–15, 17], то имеем граничные линии. Граничными линиями являются критические линии уровня функции u (t), t g C . Тогда в качестве рассматриваемых областей возьмем эти линии.

Заметим, что оценки решения задачи (1), (2) зависят только от особых точек, собственных значений матрицы D(t). Поэтому в качестве рассматриваемой области возьмем всю комплексную плоскость удовлетворяющую условию (5).

Если точки смены устойчивости, начальная и критическая точка совпадает, то такие случаи рассмотрены в работе [2]. Рассматриваемая задача была линейная, и ограничена первым приближением. Здесь мы поступим так, чтобы эти точки не совпадали, рассматриваемые области были наибольшими, а собственные значения кратными аналитическими функциями. Случаи, при которых собственные значения есть дифференцируемые функции рассмотрены в работе [17].

Если собственные значения состоять от мнимых частей, то исследовать решение задачи (1), (2) можно как в работах [3, 4, 16]. Переходя к другом пространстве можно рассмотреть как в работах [6–8].

Выводы

Решение (1), (2) зависят от выбора собственных значений матрицы D(t) и выбора начальной точки. В работе доказана теорема, при помощи которой выполняются условия устойчивости. А также показана зависимость решения задачи не только от условий устойчивости, а также и от гармонических функций u_k (t) < 0, (k = 1,2), t g C. В данной работе областью исследования является комплексная плоскость. Следовательно, на оценки решений (1), (2) влияют только пограничные области Q₃.

Если поставим условия выбора начальной точки, то получим задачи, которые внутри рассматриваемой области собственными значениями матрицы несколько раз меняет условия устойчивости. В данном случае также доказано асимптотическая близость решений.