Асимптотика решения двухточечной краевой задачи с особыми точками

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 517.928                                       

Постановка задачи. Исследуем двухточечную сингулярно возмущенную краевую задачу:

s y" (x) + x( 1 - x)y'(x) - y(x) = f(x), 0 < x <  1 ,

y( 0) = 0 ,y( 1) = 0, где 8 — малый параметр, f G C” [0,1].

Особенность исследуемой задачи заключается в том, что сингулярно возмущенное уравнение (1) при 8^0 имеет две особые точки х =0 и х =1.

Требуется получить асимптотику решения задачи (1)-(2) на всем отрезке включая особые точки, при стремлении малого параметра к нулю.

Решение задачи. Умножая обе части уравнения (1) на выражение e

x ² ( 3 - 2 x)

6 ^s имеем:

x( 1 - x) y''(x)--

y'(x)-1 y(x) = f^, \ e

x ² ( 3 - 2 x) 6 s

e

x ² ( 3 - 2 x) 6 s

y'

— e

x^ ( 3 - 2 x)

68           f( x) “

y(x) = ^^e

£

x ² ( 3 - 2 x)

6 8

•

Из Справочника по

обыкновенным

дифференциальным уравнениям следует, что для

решения задачи (1)-(2) справедливо оценка [1]:

, x       F

\y(x)\<  , где F = max

A                x g [ 0 , 1 ]

f(x)c

x ² ( 3 - 2 x)

, A = min e xg [ 0,1 ]

x ² ( 3 - 2 x)

•

Рассмотрим соответствующее невозмущенное дифференциальное уравнение первого порядка:

^{x( 1} - ^x)y' 0 ^{(x) -} y 0 ^(x) = ^f(x) .

Умножая обе части последнего равенства на интегрирующий множитель    получаем:

x ²

1 - x

x

y'0(x) - A y0(x) = x

f(x)

x ²    ,

полученное равенство можно записать в виде:

y 0(x) 1-x

= f(x) x2

.

Интегрируя последнее равенство от x 0 до х имеем:

/  11 - X / J - Xq   } f(s) j y0 (x)--y0 (x0 )----0 =    — ds .

X             X0    X s

Выражая полученное соотношение через y 0 ( x ) получим:

y 0(x) =

X

1 - x

У о ^(x о ) 1-^0 x ₀

+ Vfs s x0

Нетрудно заметить, что полученная функция имеет две особые точки х =0 и х =1. То, что и следовало ожидать. И здесь мы выберем точку х 0 так чтобы один из этих особых точек была устранимой особой точкой.

Пусть х 0 =1, тогда имеем y₀(x)

x

1 - x

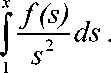
Интегрируя интеграл в правой части последнего равенства по частям можно доказать, что теперь точка х 0 =1 устранимая особая точка, а точка х =0 остается особой точкой типа полюса:

y 0(x) =

—

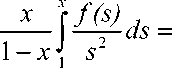
x

1 - x

x

I f(s)d 7 =

= - 77- ( f(x) - xf( 1) ) + 1 x

x

-^ff'(s)dln\s\ = 1 - x

- IT (f(x) - xf( 1)) + 1 x

f'(x) z I I ----xln \x\ + 1 - x

-

x

T^M f"(s)ln\s\ds.

1 - x

Рассмотрим левую часть уравнения (1) при x = £^а t , где 0х=0: £1 2^аy "(t) +1( 1 - £^аt)y'(t) - y(t)

если а=1/2, то имеем y"(t) + ty'(t) - y(t) - £1 /212 y'(t)

а если а=1/3, то имеем £1 /3 y"( t) - £1 /312 y'( t) + ty'( t) - y(t)

А если рассмотреть левую часть уравнения (1) при 1- x = £^а t , т.е. в окрестности точки единицы, х =1: £ 1 ^{2 а} y"( t) - ( 1 - £^а t )ty^r(t) - y(t) .

если а=1/2, то имеем y"(t) - ty'(t) - y(t) + £1 /212 y'(t)

а если а=1/3, то имеем £1 /3 y"( t) + £1 /312 y'(t) - ty’(t) - y(t) .

Асимптотическое решение краевой задачи (1)-(2) ищем в виде суммы трех рядов:

y (x) = u (x)+V (t) + w(n)

где

U(x) = UQ (x) + £u (x) + £2u2 (x) +...

v (т) = vo (т) + HV (т) + Ц2 v2 (т) +...

w(n) = w0 (n) + ^ W (n) + ^ 2 W (n) +...

x = цт , Ц = VS , 1 - x = £^₽n .

Подставляя соотношение (3) в уравнение (1) получаем:

s u"(x) + x( 1 - x)u'(x) - u(x) = f(x) - h(x), v"( т) + т v'( т ) - v( т ) - цт2 v'( т ) = h( т ), w"( П ) -П w'( П ) - w( П ) + ЦП2 w'( П ) = 0, где

h(x) = h(x) + sh(x) + s2 h2(x) +..., hk(x) — пока неизвестные функций [2-10].

Подставляя (4) в (7) и по идее метода малого параметра имеем:

x( 1 - x)u'0(x) - u0(x) = f(x) - h0(x),

x( 1 - x)u'k(x) - uk(x) = -u"k_i(x) - hk(x),k e N

Уравнений (11) и (12) будем интегрировать так чтобы точка х =1 была устранимой:

u 0 (x)=-f-hMd ds, 1 - xs как и в предыдущих работах [2-10], неизвестную функцию h0(x) выберем так чтобы u0 e C” [ 0,1 ] .

Пусть h ₀ (x) = f'( 0 )x , тогда u ₀ e C " [ 0 , 1 ] .

Действительно, z . x  ]f(s) - f'(0)s. x  xf(0) + s2 F(s).

u_n(x) =---- ₀      ds =---- ;--- d-=ds =

1 - x*       s             1 - x*        s x x                  1           F( 1) - x2F(x) 2x x

= -      ( f( 0 ) + s² F(s) ) d- = - f( 0 ) +     ----- ■       F(s)ds.

• 1    - x                     s                 1 - x        1 - x\

Аналогично определяются все h k ( x ), k =1,2,... так чтобы u_k e C ” [ 0 , 1 ],k e N.

Не сложно заметить. что при h_k(x) = - u "'_k_^( 0 )x мы достигнем своей цели.

Здесь мы определили все члены рядов (4) и (10).

Перейдем теперь к рассмотрению уравнения (8). Учитывая соотношения (5) и (10) имеем:

v"0 ( T ) + T v'0 ( T ) - v0 ( T ) = Л 0 Л,v"2 k-1(Т ) + T v'2 k-1(Т ) — v 2 k-1(Т ) = Т v2 k-2 (Т )’

v"2k(T) + T V2k(T) - v2k(T) = hk(Т) + Тv2k-1(Т)

Из краевых условий (2) и свойств пограничных функций следует, что:

v2k(0) = -Uk(0), V2k+1(0) = 0, vk (T) = 0, k = 0,1,2...

т—ад

Как нам известно, соответствующее однородное уравнение z "( t ) + tz '( t ) - z ( t ) = 0

имеет два независимых решений:

t z1 (t) = t, z2 (t) = e-t /2 +1J e T /2dt , ад где z2

(t )=

1 — c^t + c^t +..., t —— 01  —/2/2    3135      , 1\и+17e ' /2(1 -^ + —j— +...+ (-1)n+1

(2 n +1)!!

12 n

+...), t — ад,

2/2

вронскиан: W (z1, z2) = - e

Поэтому решение задачи

v"0(T) + Tv'0(T) - v0(T) = Л0)HT,T e [0,ад), v0(0) = -u0(0), v0 (T) = 0 t—ад существует, единственно и можно записать в виде

v0(t) = -pz2(T)f(0) z,(s)ses/2ds + pz.(t) z2(s)ses/2ds -u0(0)z2(t) .

0                                             ад

Аналогично определяются остальные члены ряда (5).

Перейдем к определению членов последнего ряда (6). Подставляя ряд (6) в уравнению (9) имеем:

w”0(n)-nw'0(n)-w0(n) = 0, ne[0,ад),                       (13)

w"k( n ) -n w'k( n ) - wk( n ) = -n2 w'k-1 (n ), ne [ 0, ад ), k e N.

Аналогично, из краевых условий (2) и свойств пограничных функций следует, что:

w2k(0) = -ut(1), w2k+1(0) = 0, Wk (n) = 0, k = 0,1,2...                  (14)

n—ад

Однородное уравнение Wⁿ ₀ ( n ) - n w' 0 ( n ) - W 0 ( n ) = 0 имеет независимые решения

n w0,1 (n) = en /2, w0,2(n) = en /2 Je s /2 ds, вронскиан W(w01,w02) = en /2 [ ].

ад

Поэтому решение задачи w''0(n) - n w'0(n) - W0(n) = 0, n e [0,адЛ

W0(0) = -u0(1), W0(n) = 0, n—ад существует, единственно и представимо в виде:

w o ⁽ П ) =

- A uo(0)en2/2 f e-s2/2ds. π∞

А неоднородное уравнение z''(n) — Пz'(П) — z(П) = f(П) , ne [0, ^), с краевыми условиями z ( o) = A, lim z(n) = 0 имеет решение η→∞

• 2    A                                  S   .2/,

^z( n ) = -j=w 02 ⁽ n ) ^- w 01 ⁽ n ) f ^f(s) f ^{e   d T ds} + w 02 ⁽ n ) f ^f(s)ds .

Vⁿ                   0       »                      0

Используя последнее соотношение сможем записать решения задач (15)-(16).

Таким образом нами определены все члены рядов (4), (5) и (6). Тем самым все слагаемые функций в (3).

Нами доказана теорема.

Теорема. Для решения сингулярно возмущенной краевой задачи (1)-(2) на отрезке х ∈ [0,1] при стремлении малого параметра к нулю справедливо разложение ∞∞

y (x) = X e kuk (x) + X ek/2 (vk (t) + wk (n)).

• k = 0               k = 0