Aspects of determining the aggregative stability of water suspensions of mineral powders for building composites
Автор: Frolova M.A.
Журнал: Nanotechnologies in Construction: A Scientific Internet-Journal @nanobuild-en
Рубрика: Manufacturing technology for building materials and products
Статья в выпуске: 1 Vol.14, 2022 года.
Бесплатный доступ
Introduction. When using water suspensions of finely dispersed mineral systems of natural and anthropogenic origins as active agents in the production of concrete composites, an important factor in their effective use is to ensure the aggregative and sedimentation stability of solid phase particles before adding the solid phase into the reaction mixture. Methods and materials. The paper provides an algorithm for quantifying stability criteria according to the DLVO theory provisions as exemplified by a suspension of fine polymineral sand powder from the Kholmogorskoye deposit in the Arkhangelsk region (average particle size is 195 nm). In order to successfully assess the aggregative stability of this colloidal system, it is necessary to conduct experiments for determining the analogue value of the Hamaker constant, which was 0.5 •10–20 J for the mineral sand studied, in addition to experiments for determining the zeta potential of particles. This paper presents the results of the analysis according to the criteria of the value of the interaction energy (Uint) and the sedimentation rate (Vsed) of a polymineral sand dispersed system (water suspension) calculated taking into account the analogue value of the Hamaker constant, zeta potential and dimensional characteristics of its solid phase particles, physicochemical properties of the dispersion medium. Results and discussion. It is shown that the determining factor of the aggregative stability of the suspension is the electrostatic barrier for particle interaction. Theoretical calculation showed that the aggregative stability of the system may be affected by its particles reaching their zeta potential of approximately 10–4 mV (a nearly isoelectric state). It is proposed to use the kinetic parameter of sedimentation – its velocity – to assess the kinetic (sedimentation) stability of this suspension – resistance to gravity, i.e. the ability to resist the dispersed system stratification due to the difference in particle densities between the dispersed phase and dispersion medium. Conclusion. The sedimentation rate is Vsed ≈ 4 nm/sec for the object under study in water dispersion medium with the averaged dimensional characteristics of 195 nm. At such a rate of solid phase particle precipitation, a dispersed system based on finely crushed polymineral sand from the Kholmogorskoye deposit can be considered sedimentatively stable.
Concrete composite, aggregative and sedimentation stability, analogue value of the Hamaker constant, sedimentation rate
Короткий адрес: https://sciup.org/142231175
IDR: 142231175 | DOI: 10.15828/2075-8545-2022-14-1-5-10
Текст научной статьи Aspects of determining the aggregative stability of water suspensions of mineral powders for building composites
Original article
Currently, processing methods associated with the use of pre-activated highly dispersed systems as additives have become widespread in the concrete composite production industry. In this case, a fairly wide range of materials of natural (mainly rocks of various genesis) and anthropogenic (fly ash, waste concrete scrap, etc.) origin is used as raw materials [1–3]. However, the introduction of such additives, the content of which in the cement-sand mixture usually does not exceed 10%, is associated with certain process difficulties of their uniform distribution over the entire composite volume. This problem is solved quite simply by introducing highly dispersed systems into the reaction mixture in the form of suspensions where mixing water is a dispersion medium. However, in this case it is necessary to solve the problem of providing the aggregative stability of solid phase particles in mineral suspensions. The simplest method in this case is to introduce additional surfactants of different nature into the colloidal solution. The consequence of this method is
MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS an inevitable decrease in the activity of highly dispersed particles due to the formation of stabilizing surface layers of surfactants. The intensity of interactions at the interface leads to the formation of a “film phase” of the matrix material (mineral particles) with the properties that differ from the matrix ones [4]. Therefore, the state of bordering surface layers formed on the dispersed phase particles is critical for aggregatively stable colloidal systems [5–7]. A modern theory of colloidal stability (DLVO theory) has been developed based on the concepts of surface forces and disjoining pressure in thin films evolved by B.V. Deryagin [8]. This theory is based on the energy balance of forces manifested between the dispersed system particles spontaneously moving close to each other. Thus, repulsive forces (Frep) of electrostatic nature arise in an aggregatively stable system when the surface layers of converged particles of the same nature overlap. The dispersed system is aggregatively stable with a sufficient value of the energy repulsion barrier. In this case, the convergence of particles to a distance where attractive forces (Fatt) prevail is impossible.
From the point of view of colloidal chemistry [9], the surface of highly dispersed particles distributed in a liquid carries a certain charge, due to which an electrical double layer (EDL) is formed. According to the DLVO theory, the presence of the EDL on the surface of particles creates an electrostatic repulsion barrier ensuring the stability of dilute colloidal systems.
The value of the interaction energy ( U int) between two particles of a dispersed system is calculated using the potential dependences of this total energy value on the distance between the particles in the area where their surface layers overlap ( h ), which does not exceed 20 nm. Then
Vint — ^rep Vatt ,
where U rep and U att are the energies of repulsion and attraction, respectively.
The dispersed system is aggregatively unstable at U int< 0, and stable at U int > 0. In turn, the DLVO theory [8, 9] provides the following equations for calculating the energy of attraction and repulsion between interacting particles:
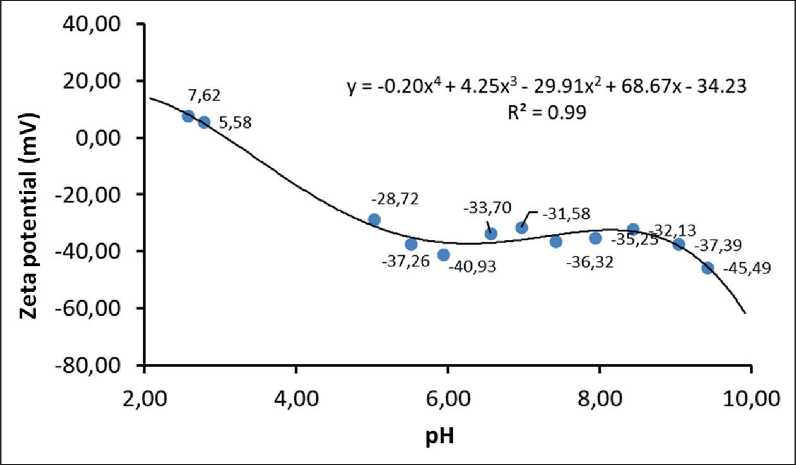
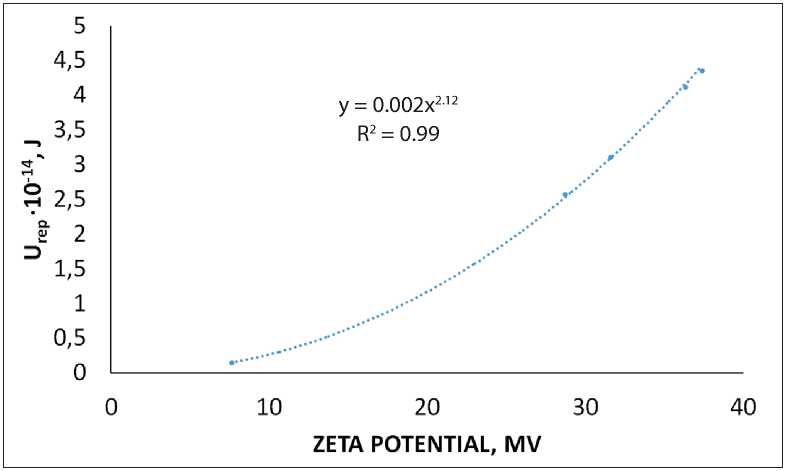
[7rep = 27T££0 _ Ar_ att 12/1 , where r is the radius of particles; φ is the surface potential (numerically equal to ζ potential); υ is the inverse of the surface layer thickness (υ=1/λ), I is the ionic strength of the solution, I = 1/2 ∑(ci zi2), ci is the concentration of ions in the solution, zi is the ion charge value; F is the Faraday’s constant, F = 9.65•104 C/mol; R is the universal gas constant, R = 8.31 J/(mol·K); ε is the dispersion medium permittivity, F/m; ε0 is the vacuum permittivity, ε0 = 8.85•10–12 F/m; А – complex constant of molecular interaction forces (Hamaker constant). Therefore, based on equations (2), (3) and (4), the sign of the dispersed system Urep will be determined by the nature of its constituent components. Thus, the nature of the dispersed phase is determined by the value of the A constant, and the dispersion medium is determined by the value of the I characteristic. The dependent variable associated with the nature of the dispersed phase and the dispersion medium is the value of the electrokinetic potential (ζ). The modern instrumental base of physicochemical analysis methods makes it quite easy to solve the problem of zeta potential quantification, e.g. when measuring the rate of particle electrophoresis. In addition, when calculating the energy characteristics of mineral particle interaction in the water dispersion medium only (without the addition of electrolytes that change e.g. the system pH), it is possible to simplify the Urep calculation scheme by assuming I≈0. Then we will obtain the following equation for 20 0С: Vrep (31.05 10 ф i7h^ ^. (5) At the same time, it is known that the dispersion medium pH can significantly change the ζ potential value, up to the recharge of the particle surface. In this case, the aggregative stability characteristics of the dispersed system according to the Uint criterion will need to be calculated taking into account changes in the solution ionic strength values: ^int = 2яее0<р2г1п(1 + eSft) - ^-. (6) The key element of this approach to the aggregative stability assessment of dispersed systems consists in determining the Hamaker constant value (A). The A value for some substances (and systems) can be found in the reference literature [10–13]. However, the developed theoretical provisions of the physicochemistry of surface phenomena [14] allowed us to apply the Hamaker constant calculation method based on determining the equilibrium contact angle (θ) of the analyzed material surface wetting with liquids having known surface tension values (σj) [15] with the dependence proposed by B.V. Deryagin as a basic equation: 5 = ( ее0ЯГ^ cos6 = 1 + A* 1277471/1^^ MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS Where hmin is the smallest film thickness that corresponds to the van der Waals distance (0.24 nm) [16]. In this case, it should be noted that this experimental approach makes it possible to determine not the absolute value of the unknown quantity, but the possible analogue value of the Hamaker constant (A*) [17, 18]. Therefore, in our opinion, an urgent task is to create a database of reference data related to the analogue value of the Ha-maker constant for systems of various nature (natural and antropogenic origin). A* can be a criterion for evaluating the correctness of the choice of dispersed components and the main conditions for their effective use determining the parameters under which the dispersed system is aggregatively stable (unstable). Another criterion used to assess the ability of particles to maintain distribution throughout the dispersion medium is the sedimentation rate (Vsed). In suspensions with dispersed phase particles ranging in size from 10–7 to 10–4 m, Brownian motion is practically absent, and the sedimentation rate is determined by the equation [19–22]: where ρ is the density of dispersed phase particles (kg/m3); ρ0 is the density of the dispersion medium (ρ = 998 kg/m3 is assumed for water at 20 0С); g is the acceleration of gravity, g = 9.81 m/s2; η is the dispersion medium viscosity (η = 8.9•10–4 Pa•s for water suspension at 20oС). This paper presents the results of the analysis according to the criteria of Uint and Vsed of the polymineral sand dispersed system (water suspension) (p = 2630 kg/m3) calculated taking into account the analogue value of the Hamaker constant, zeta potential and dimensional char- acteristics of its solid phase particles, physical and chemical properties of the dispersion medium. METHODS AND MATERIALS The analysis of the results obtained by us earlier and published in [16, 18, 19] was carried out according to the above calculation scheme. The polymineral quarry sand from the Kholmogorskoye deposit (Kholmogorsky district, Arkhangelsk region) was chosen as the object of research. Fine powder with the mean volume diameter of 195±95 nm was obtained by mechanical grinding at the planetary ball mill. The zeta potential of solid phase particles was determined by measuring the rate of electrophoresis in a prepared water suspension at pH in the range of 2.5–9.5. Changes in the dispersion medium pH were carried out by acidifying the solution with hydrochloric acid or alkalizing the solution with sodium hydroxide. Energy parameters of particle interaction were calculated using the analogue value of the complex Hamaker constant (A*), which we determined for this sand based on the results of experiments described in the paper [21]. This value was A*= 0.5.10-20J. RESULTS AND DISCUSSION Figure 1 shows the experimental results obtained in the paper [21]. Table 1 shows pH values of the dispersion medium selected (arbitrarily) for calculations, zeta potential of particles, corresponding ionic strength of the solution and Uint values calculated according to equations (5) and (6). Fig. 1. Functional dependence of zeta potential changes on the dispersion medium pH [21] MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS Table 1 рН, ζ potential, I of the dispersed system and Uint рН 2.5 5.0 7.0 8.0 9.0 ζ potential, mV 7.62 –28.72 –31.58 –36.32 –37.39 I, mol/l 3•10–3 10–4 0 10–5 10–4 Uatt, J 1.29•10–29 1.29•10–29 1.29•10–29 1.29•10–29 1.29•10–29 Urep, J 1.53•10–15 2.58•10–14 3.11•10–14 4.12•10–14 4.36•10–14 Uint, J 1.53•10–15 2.58•10–14 3.11•10–14 4.12•10–14 4.36•10–14 Particle interaction energy calculations (Table 1) showed that the presence of an electrostatic barrier in the suspension under consideration allows us to talk about the aggregative stability of the system (Uint > 0) over the entire range of measured pH. The energy of van der Waals attraction between particles is almost 10 orders of magnitude lower than the energy of electrostatic repulsion, i.e. the electrostatic factor contributes to the preservation of aggregative stability in this system. Figure 2 shows a dependence of Urep = f(ζ), which is described by a mathematical equation (R2 is the approximation confidence, 0.99): Urep = 0.002<212. (9) Using this functional relationship, it can be concluded that the suspension becomes aggregatively unstable only at the ζ potential value of approximately 10–4 mV Urep< Uatt (the system nearly reaches its isoelectric state). The calculations carried out showed that the water suspension of particles of polymineral sand from the studied deposit features by the ability of the dispersed phase to maintain the degree of dispersion, i.e. particle sizes, unchanged in time and resist their unification throughout the studied pH range. It seems important to assess the kinetic (sedimentation) stability of this suspension – resistance to gravity, i.e. the ability to resist the dispersed system stratification due to the difference in particle densities of the dispersed phase and the dispersion medium. As a quantitative criterion, we can use the kinetic parameter of sedimentation – its velocity calculated by equation (8). For the object under study in an aqueous dispersion medium with the averaged dimensional characteristics of 195 nm, the sedimentation rate is Vsed ≈ 4 nm/sec. At such a precipitation rate of solid phase particles, a dispersed system based on finely fragmented polymineral sand from the Kholmogorskoye deposit can be considered sedimentationally stable. Fig. 2. Functional dependence of the Urep = f(ζ) form MANUFACTURING TECHNOLOGY FOR BUILDING MATERIALS AND PRODUCTS CONCLUSION In order to assess the aggregative stability of mineral dispersed systems based on the comparison of particle interaction energy in the classic case taking into account the DLVO theory provisions, it is necessary, in addition to studying their electrokinetic properties, to perform works on determining the analogue Hamaker constant value. Therefore, studies aimed at experimentally determining the quantitative values of this characteristic and compiling a database for finely dispersed mineral systems of various origin are of particular interest when choosing the nature of the material and establishing formulation process factors for its use.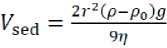
Список литературы Aspects of determining the aggregative stability of water suspensions of mineral powders for building composites
- Kharkhadin A.N., Nelyubova V.V., Popov A.L., Strokova V.V. Milling topology of micro- and nanodispersed materials of various mineral composition. Regional Architecture and Construction. 2017; 2(31): 5–12.
- Kobzev V.A., Sivalneva M.N., Nelyubova V.V. Highly concentrated aluminosilicate binding suspension made of granodiorite. Bulletin of the Belgorod State Technological University named after V.G. Shukhov. 2019; 14(66): 73–83.
- Morozova M.V., Ayzenshtadt A.M., Akulova M.V., Frolova M.A., Shamanina A.V. Evaluation of the possibility to use powders of polymineral silica-containing sands as a hydrophobizing coating. Nanotechnologies in Construction. 2021;13(4): 222–228. DOI: 10.15828/2075-8545-2021-13-4-222-228.
- Korolev E.V. Prospects for building materials science development. Regional Architecture and Construction. 2020; 3: 143–159.
- Lunina M.A. Main regularities of aggregative stability and coagulation of lyophobic colloidal systems. In: Proceedings of the 10th International Conference on Magnetic Fluids, September 2002, Plyos, Russia. 2002. p. 4–10.
- Ayzenshtadt A.M., Drozdyuk T.A., Danilov V.E., Frolova M.A., Garamov G.A. Surface activity of concrete waste powders. Nanotechnologies in Construction. 2021; 13(2): 108–116. DOI: 10.15828/2075-8545-2021-13-2-108-116.
- Ayzenshtadt A.M., Danilov V.E., Drozdyuk T.A., Frolova M.A., Garamov G.A. Integral quality indicators of waste concrete for reuse. Nanotechnologies in Construction. 2021; 13(5): 276–281. https://doi.org/10.15828/2075-8545-2021-13-5-276-281
- Danilov V.E., Shinkaruk A.A., Ayzenshtadt A.M., Drozdyuk T.A., Frolova M.A. Aggregative stability of the water suspension of finely dispersed basalt. Nanotechnologies in Construction. 2018; 10(6): 77–90. DOI: dx.doi.org/10.15828/2075-8545-2018-10-6-77-90.
- Deryagin B.V. Theory of stability of colloids and thin films. Moscow: Nauka. 1986.
- Volkov V.A. Colloidal chemistry. Surface phenomena and dispersed systems: Textbook. 2nd ed. St. Petersburg: Lan Publishing House; 2015.
- Boynovich L.B. Long-range surface forces and their role in nanotechnology development. Uspekhi Khimii. 2007; 76(5): 510–528.
- Tsao Guozhong, Ying Wang. Nanostructures and nanomaterials. Synthesis, properties, and applications. Transl. from English by A.I. Efimova, S.I. Kargov. Moscow: Nauchny Mir; 2012.
- Roldugin V.I. Physical chemistry of surfaces: Textbook-monograph. Dolgoprudny: Intellect Publishing House; 2008.
- Ayzenshtadt A.M., Lesovik V.S., Frolova M.A., Tutygin A.S. Physical chemistry elements of finely dispersed systems. Arkhangelsk: NArFU; 2015.
- Deryagin B.V., Churaev N.V., Muller V.M. Surface forces. Moscow: Nauka; 1985.
- Frolova M.A., Tutygin A.S., Ayzenshtadt A.M., Lesovik V.S., Makhova T.A., Pospelova T.A. Criterion for evaluation of surface energy properties. Nanosystems: Physics, Chemistry, Mathematics. 2011; 2(4): 120–125.
- Deryagin B.V., Churaev N.V. Wetting films. Moscow: Nauka; 1984.
- Ayzenshtadt A.M., Korolev E.V., Drozdyuk Т.А., Danilov V.E., Frolova M.A. Potential approach to evaluation of dispersive interactions in powder systems. Physics and Chemistry of Materials Treatment. 2021; 3: 40–48. Available from: doi: 10.30791/0015-3214-2021-3-40-48.
- Danilov V.E., Korolev E.V., Ayzenshtadt A.M. Measuring the contact angles of powders by the sessile drop method. Inorganic Materials: Applied Research. 2021; 12(3): 794–798.
- Gelfman M.I. Kovalevich O.V., Yustratov V.P. Colloidal chemistry: textbook. St. Petersburg: Lan; 2010.
- Danilov V.E. Mechanical synthesis of finely dispersed silica for sodium polysilicate-based binder production. In: Construction – the Formation of Living Environment: Proceedings of the XX International Interuniversity Scientific and Practical Conference. Moscow: NRU MGSU; 2017. p. 798–800.
- Ayzenshtadt A.M., Frolova M.A., Sokolova Y.V., Drozdyuk T.A. (2022) Control of Physical and Chemical Processes at the Phase Boundary in the Formation of Building Composites. Digital Technologies in Construction Engineering. Lecture Notes in Civil Engineering. 2022; 173: 209–215 Springer, Cham. Available from: https://doi.org/10.1007/978-3-030-81289-8_27.


