Аспекты влияния инфляции на процесс аккумулирования денежных средств при приобретении дорогостоящего имущества

Рассмотрим ситуацию, когда в определенный момент времени Некто принял решение приобрести со временем определенный дорогостоящий актив. Для определенности предположим, что речь идет о приобретении вожделенной новой квартиры, которую Некто хочет приобрести, но на которую у него пока не хватает денег.

Пусть ожидаемое удорожание целевого актива за годовой период (инфляция) равно i (%/год). В момент принятия решения ( t ₀) на руках у Некто имеется сумма S ₀ (р.). Текущая стоимость целевого актива составляет S_a (р.). Депозитная ставка в банке равна R_d (%/год), а ставка кредитования – R_cr (%/год), при этом по условиям кредитного договора (предположим) проценты начисляются на остаток суммы кредита, а льготный период (кредитные каникулы) отсутствует.

В этой ситуации Некто способен ежепериодно (ежемесячно) аккумулировать целевую сумму в размере S ₁ р./мес. Однако перед тем, как начать заниматься накопительством, как правило, Некто начинает строить некий финансовый план и сам себе задавать различные вопросы, ответы на которые не так уж и очевидны. В поисках ответов на них можно изучить анналы поисковых систем интернета, особенно в части знаменитых «шести функций сложного процента». Отдельные пытливые личности даже могут настолько увлечься процессом обдумывания различных аспектов аккумулирования и инвестирования средств, что могут незаметно для себя «проглотить» ряд бестселлеров и фолиантов на эту тему ¹.

Рассмотрим специфические вопросы, возникающие в подобных ситуациях. В них автор настоящей статьи попытался соблюсти «золотую середину» между известными «банальностями» и «скучно длинным» академизмом раскрытия тематики. Для удобства читателей они структурированы в форме конкретных вопросов и развернутых решений в поисках ответов на них.

Вопрос 1

Через сколько периодов (n, мес.) Некто сможет накопить достаточную для приобретения целевого актива сумму?

Сначала надо определить, сколько будет стоить целевой актив через n периодов (мес.):

n

FV t = V t ^⎛⎜_⎝ 1 + ₁ ⁱ ₂ ^⎞⎟_⎠,                                                                                            (1)

где FV_t – стоимость целевого актива через n периодов;

V_t – текущая стоимость целевого актива в момент оценки; i – годовая инфляция (% годовых/100).

Определим, какая сумма ( S ) накопится за этот период n на двух целевых депозитах, на первый из которых будет положена вся имеющаяся у Некто сумма ( S₀ ), а на второй начиная с конца первого периода будет ежемесячно поступать сумма S ₁. Прежде всего запишем, как чаще всего определяется сумма такого накопления в банке за период (временной интервал) ( n , k ), где n – полное количество лет накопления, k – количество месяцев сверх полного количества лет (учитывая, что капитализация процентов в банках, как правило, осуществляется один раз в год, а внутри года начисление процентов осуществляется по правилу простого процента):

S = S 0

^k ₁ ^× ₂ ^{R d} + ( 1 + R d ) ^{n ⎤}⎥+ S 1

k × R d ₊ ( 1 + R d ) ⁿ - 1 12         R d

Для ответа на поставленный вопрос следует приравнять расчетную будущую сумму целевого актива ( FV_t ) к накопленной на депозитах сумме ( S ), то есть приравнять равенство (1) к равенству (2), и определить из нового равенства искомое значение n опцией «Подбор параметра». Принимая во внимание тот факт, что в равенстве (2) имеется более одного неизвестного параметра ( n и k ), что осложняет (делает невозможным) использование опции «Подбор параметра», для последующего решения сделаем предположение о том, что капитализация процентов осуществляется ежемесячно (такое предположение довольно реалистично, поскольку в настоящее время банки предлагают депозиты с ежемесячной капитализацией процентов). Тогда вместо равенства (2) получим следующее выражение:

n

S = S ^⎛ 1 + ^{R d ⎞}+ 12 S 0 ⎜_{⎝ 12} ⎟_⎠            1

( 1 + R d 12 ) ⁿ

В случае поступления на второй депозит первой суммы сразу же в начале срока накопления вместо выражения (3) следует использовать следующее выражение:

n

S = S ^⎛ 1 + ^{Rd ⎞}+ S

0 ⎜_⎝              ⎟_⎠ 1

( 1 + R_d 12 )^{( n +1 )} - 1 Rd I 12

Теперь для получения ответа на первый вопрос следует приравнять расчетную будущую сумму целевого актива ( FV_t ) к накопленной на депозитах сумме ( S ), то есть приравнять равенство (1) к равенству (3) или (4), и определить из нового равенства искомое значение n опцией «Подбор параметра».

Пример 1

Пусть S ₀ = 1 млн р., V_t = 8 млн р., S ₁ = 0,15 млн р./мес., i = 12%/год, R_d = 6%/год. Пусть известно, что первый взнос на пополняемый депозит Некто внес в конце первого периода. Тогда для определения n (исчисляемого в месяцах), как указано выше, необходимо выполнить равенство:

nn

V ^⎛ 1 + ^{i ⎞}= S ^⎛ 1 + ^{R d ⎞}+ 12 S ^{t ⎜}⎝ 12 ^⎟⎠ ^{0 ⎜}⎝ 12 ^⎟⎠            ¹

( 1 + R d 12 ) ⁿ - 1

которое при заданных параметрах соответствует равенству:

nn

8 ×^⎛ 1 + ^{0 , 12 ⎞} = 1 ×^⎛ 1 + ^{0 , 06 ⎞} + 12 × 0 , 15 × ⎜_⎝                 ⎟_⎠⎜_⎝                 ⎟_⎠                   ^,

( 1 + 0 , 06 12 ) ⁿ - 1 0 , 06

Решение этого равенства посредством применения компьютерной опции «Подбор параметра» приводит к значению n = 120,1 мес. или более 10 лет.

Указанное решение определения искомого срока накопления включает частный случай, решение которого заслуживает отдельного рассмотрения, поскольку допускает применение иного способа решения.

Такой частный случай при рассмотрении первого вопроса возникает в ситуации, когда величина депозитной ставки равна ожидаемому темпу удорожания целевого актива (то есть R_d = i ). В этом случае условие (5) сводится к следующему выражению:

nn

V ^⎛ 1 + ^{i ⎞}= S ^⎛ 1 + ^{i ⎞}+ 12 S t ⎜_{⎝ 12} ⎟_⎠ 0 ⎜_{⎝ 12} ⎟_⎠            1

( 1 + i 12 ) ⁿ - 1

из которого значение параметра n можно рассчитать в явном виде:

n =

12 S 1 i ( S 0 - V t ) + 12 S 1

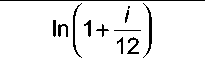
Пример 2

Пусть S ₀= 1 млн р., V_t = 8 млн р., S ₁ = 0,15 млн р./мес., i = 6%, R_d = 6%.

Для определения n применим условие (7):

ln

12 × 0 , 15

n =

^⎢⎣ 0 , 06 × ( 1 - 8 ) + 12 × 0 , 15 ^⎥⎦ ₌ ln ( 1 , 340 )

0 , 06

ln 1 +

⎜⎝

ln ( 1 , 005 )

= 51 , 29 .

То есть для накопления искомой суммы (при нехватке 7 миллионов рублей) потребуются 51,29 месяца, или 4,27 года.

Вопрос 2

Какую максимальную сумму, измеряемую в текущих ценах, можно накопить при отсутствии защиты от инфляции? Или при какой максимальной сумме перестанет расти покупательная способность периодически пополняемых накоплений при отсутствии защиты от инфляции?

Определим верхнюю границу накоплений, свыше которой при фиксированном периодическом накопительном взносе и при определенном уровне инфляции за период между пополнением взноса дальнейшее накопление становится нецелесообразным ввиду потери покупательной способности депозита (вклада). Сначала для наглядности определим уровень такого накопления народным способом «в чулке» или «в кубышке»:

• 1)    если средства начать откладывать начиная с конца текущего периода, то за бесконечное число периодов удастся накопить средства для приобретения имущества, стоимость которого в текущих ценах составляет:

S_к = S ₁ / i ; (8)

• 2)    если средства начать откладывать начиная с начала текущего периода, то за бесконечное число периодов удастся накопить средства для приобретения имущества, стоимость которого в текущих ценах составляет:

S 1 S 1

° к =         = ° 1 +   ^.

1 - —      '

1 + i

Накопление средств свыше этой суммы при тех же условиях будет лишено смысла из-за того, что инфляционные потери «кубышки» за один период между ее пополнениями будут превышать сумму ее пополнения, в результате чего покупательная способность накоплений перестанет увеличиваться.

Время накопления такой максимальной «кубышки» ( k ₁) определяется просто:

k ₁ = ( S_k – S ₀) / S ₁.                                                                                 (10)

Пример 3

Пусть S ₁ = 0,1 млн р./мес., i = 7%/год.

Из выражений (8) и (9) определим максимально возможный уровень накопления в текущих ценах. Если начать копить через один период (в конце текущего периода), то согласно выражению (8) удастся накопить на имущество, стоимость которого в сегодняшних ценах составляет 0,1 / (0,07 / 12) = 17,14 млн р. (более точно при использовании сложных процентов: 0,1 / (1,07^{(1 / 12)} – 1) = 17,69 млн р. ). Если же начинать копить с сегодняшнего дня, то согласно выражению (9) удастся накопить лишь на имущество, стоимость которого в сегодняшних ценах составляет 0,1 + 17,69 = 17,79 млн р.

В соответствии с выражением (9) определим сумму накоплений авансовой «кубышки», свыше которой инфляционные потери «кубышки» за один период между пополнениями будут превышать сумму пополнения 0,1 / [1 – 1 / (1 +0,07 / 12)] = 17,24 млн р. (более точно при использовании сложных процентов 0,1 / [1 – 1 / (1 + 0,00564)] = 17,79 млн р . ).

Что на практике означает сумма 17,79 миллиона рублей для условий нашего примера? Она означает, что попытка прибавления к ней очередной порции накоплений в размере 0,1 миллиона рублей с точки зрения повышения покупательной способности накоплений будет обречена на провал, поскольку в течение месяца инфляционное обесценение возросшей суммы 17,89 миллиона рублей приведет к снижению ее покупательной способности до прежнего уровня: 17,89 / (1 + 0,07 / 12) = 17,79 млн р.

Из этого примера следует, что максимальная сумма накоплений беспроцентной «кубышки» достигается тогда, когда инфляционные потери «кубышки» за один период между пополнениями будут превышать сумму пополнения.

Определим для условий этого примера время накопления максимальной суммы «кубышки». Предположим, что к моменту принятия решения о таком накоплении Некто уже располагал суммой 1 миллион рублей. Тогда согласно выражению (10) k1 = (17,79 – 1)/0,1 = = 168 мес.

Вопрос 3

Какую максимальную сумму, измеряемую в текущих ценах, можно накопить при наличии частичной защиты от инфляции? Или при какой максимальной сумме перестанет расти покупательная способность периодически пополняемых накоплений при наличии частичной защиты от инфляции?

Теперь определим верхнюю границу накоплений, свыше которой при фиксированном периодическом накопительном взносе и при определенном уровне инфляции за период между пополнением взноса дальнейшее накопление становится нецелесообразным ввиду потери покупательной способности депозита (вклада). При этом учтем частичную защиту от инфляции, создаваемую процентами на депозите. Если средства начинать откладывать начиная с начала текущего периода, то удастся накопить сумму для приобретения имущества, максимальная стоимость которого в текущих ценах составляет:

■ _S ( i + ' )_o . s ^’ + R d )

'pre = i-Rd "S1+ i-R где Spre – сумма ежепериодных авансовых накоплений величины S1, эквивалентная максимальной стоимости целевого актива в текущих ценах; остальные обозначения соответствуют ранее принятым.

Если же средства начинать откладывать начиная с конца текущего периода, то удастся накопить сумму для приобретения имущества, максимальная стоимость которого в текущих ценах составляет:

S

post

S ( 1 + R d )

^^^^^^^B

R d

где S_post – сумма ежепериодных накоплений величины S ₁ (откладываемых постнумерандо), эквивалентная максимальной стоимости целевого актива в текущих ценах.

Отметим, что в числителе и знаменателе выражений (11) и (12) следует использовать одинаковые по размерности величины.

Пример 4

Пусть S ₁ = 0,1 млн р./мес., i = 12%/год, R_d = 6%/год. Пополнения депозита осуществляются пренумерандо (авансом в начале каждого периода).

Из выражения (11) определим сумму накоплений, эквивалентную максимальной стоимости целевого актива в текущих ценах. Для этого учтем, что поскольку пополнение депозита осуществляется один раз в месяц, при вычислении S_pre следует использовать процентные ставки не в годовом, а в месячном формате:

_о      0 , 1 х ( 1 + 0 , 01 )

S_Drв == 20 , 2 .

^pre    0 , 01 - 0 , 005

То есть при таких условиях удастся накопить лишь на имущество, стоимость которого в текущих цена составляет 20,2 миллиона рублей.

Теперь предположим, что в этом примере пополнения депозита осуществлялись бы в конце периода. Тогда максимальная сумма накоплений в текущих ценах согласно выражению (12) стала бы равной:

_ 0 , 1 х ( 1 + 0 , 005 )

'^                                                    ^—^z , 1 .

^post 0 , 01 - 0 , 005

То есть сумма составила бы 20,1 миллиона рублей (заметим, что разница между S_pre и S_post составляет в точности величину S ₁ = 0,1 млн р. ).

Вопрос 4

За какое время инфляционные потери за один период сравняются с суммой ежепе-риодного пополнения накоплений? Или за какое время перестанет расти покупательная способность периодически пополняемого депозита?

Определим срок ( k ₂), по истечение которого дальнейшее накопление средств лишено смысла ввиду превышения инфляционных потерь накоплений за период между пополнениями депозита над суммой их прироста.

Сначала рассмотрим случай накопления «в кубышке». Максимальная сумма накоплений была определена в выражениях (8) и (9). Срок ( k ₂), по истечение которого дальнейшее накопление средств становится лишенным смысла, может определиться приравниванием суммы максимальных накоплений к сумме ежемесячного накопления, умноженной на искомое время накопления ( k ₂), откуда в зависимости от типа накопления (авансового или в конце периода) получим:

k _{2 pre} = 1 + 1 / i ;                                                                                               (13)

k 2 post = 1 / i ,                                                                                                          (14)

где k _{2 pre} – срок накопления максимальной суммы, сверх которой дальнейшее накопление лишено смысла, при использовании авансового пополнения депозита;

k _{2 post} – срок накопления максимальной суммы, сверх которой дальнейшее накопление лишено смысла, при использовании пополнения депозита постнумерандо (в конце периода).

Пример 5

Пусть i = 12%/год.

Из выражения (14) определим срок накопления суммы S_post при условии осуществления ежемесячных пополнений депозита в конце периода:

k _{2 post} = 1 / 0,01 = 100 мес. = 8 лет и 4 месяца .

Теперь определим срок достижения максимальной покупательной способности депозита в случае накопления средств на пополняемом депозите. Максимальная сумма накоплений была определена в выражениях (11) и (12). Срок (k2), по истечение которого дальнейшее накопление средств становится бессмысленным (ввиду прекращения роста его покупательной способности), можно определить приравниванием суммы максимальных накоплений к сумме ежемесячного накопления, умноженной на будущую стоимость аннуитета за искомое время накопления (k2):

• 1)    при авансовом пополнении депозита:

_ 1 + i _

S,----- = S

• 1    i - R d

( 1 + R d ) k 2 ⁺1 - 1

• 2)    при пополнении депозита постнумерандо:

1 + R d = _S ( 1 + R d ) k ² - 1

i - R d    ¹      R d

откуда в зависимости от типа накопления (авансового или в конце периода) получим:

1) при авансовом пополнении депозита:

in 1 1 + R d

2 i + 1 - R d '

k 2 pre =

in ( 1 + R d )

- 1 ;

• 2)    при пополнении депозита постнумерандо:

  in 1 1 + R d

  
  

  k 2 post

  
  

  1 + R d ) i - R d ^J

  
  

  in ( 1 + R d )

  
  
  
  

Пример 6

Пусть i = 12%/год, R_d = 6%/год.

Определим сроки накопления сумм S_post и S_pre при условии осуществления ежемесячных пополнений депозита. Подставляя условия примера в выражения (17) и (18), получим:

• 1)    при авансовом пополнении депозита:

  2 pre

  
  

  in 1 1 + 0 , 005 x

  
  

  2 x 0 , 01 + 1 - 0 , 005 ^

  0 , 01 - 0 , 005 J

  
  

  in ( 1 + 0 , 005 )

  
  

  - 1 = 139 , 47 ;

  
  

  in 1 1 + 0 , 005 x

  
  

  k 2 post =

  
  

  1 + 0 , 005 ^

  0 , 01 - 0 , 005 J

  
  

  in ( 1 + 0 , 005 )

  
  

  = 139 , 47 .

  
  

Таким образом, в обоих случаях срок, в течение которого депозиты достигнут своего предела покупательной способности, составляет 139,5 месяца. Если, допустим, вкладчик будет пополнять депозит ежемесячно по 100 тысяч рублей, то за этот срок он накопит 20,199 миллиона рублей в случае авансового депозита или 20,099 миллиона рублей в случае депозита постнумерандо. Сравнивая этот пример с предыдущим, можно сделать вывод о том, что при наличии частичной (депозитной) защиты от инфляции период накоплений, в течение которого продолжится увеличение покупательной способности накоплений (депозита), становится больше, чем при отсутствии такой защиты.

Вопрос 5

За какое время потери от накопленной инфляции сравняются с суммой пополнения накоплений?

Определим срок ( k ₃), по истечение которого дальнейшее накопление средств становится нецелесообразным ввиду превышения инфляционных потерь за весь период накоплений над суммой их прироста. Это условие при использовании принятых обозначений и с учетом ежемесячного пополнения «кубышки» можно представить в следующем виде:

(                  ^        (                   '

„ ^s i   + s--^— + ... + s--^~

1 + i /12 ^J ( ¹ ( 1 + i /12 ) ² J       ( ¹ ( 1 + i /12 ) k ³ J

Или после приведения:

1 -

^k 3 ^-

( 1 + i /12 ) k ³

i 12

= 1 ,

решение которого возможно подбором параметра k ₃.

Пример 7

Определим срок ( k ₃) для условий предыдущего примера. Подставляя условия примера в выражение (20) и используя эксельную опцию «Подбор параметра», получим n = 14,02 мес. Это означает, что по истечении 14 месяцев после накопления 1,51 миллиона рублей (при накоплении пренумерандо) или 1,49 миллиона рублей (при накоплении постнумерандо) дальнейшее накопление при 12-процентной годовой инфляции во многом теряет смысл, поскольку суммарные инфляционные потери через 14 месяцев всех ранее сделанных накоплений превысят сумму пополнения депозита. На первый взгляд это не вполне очевидно, так как за один месяц теряется лишь 1510 – 1510 / (1 + 0,12 / 12) = 14,95 тыс. р. Однако с учетом уже пролежавших ранее денег (от одного до четырнадцати месяцев для каждого транша по 100 тысяч рублей) сумма их потерь достигнет почти 100 тысяч рублей.

Срок ( k ₃), по истечении которого происходит превышение инфляционных потерь суммарных накоплений за весь период накоплений над суммой их прироста (так называемая накопленная инфляция ), является одним из качественных индикаторов влияния инфляции на профиль инвестиционного проекта.

Таким образом, можно сделать промежуточный вывод о том, что при накоплении средств значимое влияние инфляции начинается по прошествии срока k ₃, тогда как критический уровень ее влияния достигается по прошествии срока k ₁.

Теперь рассмотрим более цивилизованный способ накопления средств на банковском депозите. В этом случае для определения значения срока ( k ₃) вместо выражения (20) следует использовать следующее условие:

1 - 1 + R d /12 ] ( 1 + i /12 J

+ ^ ^ k ₃

-

( 1 + R d /12 )

1 ( 1 + R d /12 \ ( 1 + i /12 J

R d

> = S 1 или, преобразуя,

}- S 1 = 0 ,

12 12

решение которого возможно посредством подбора параметра.

Пример 8

Пусть S ₀ = 1 млн р., S ₁ = 0,1 млн р./мес., i = 7%/год, R_d = 5%/год.

Из выражения (21) определим срок ( k ₃), по истечении которого происходит превышение инфляционных потерь суммарных накоплений за весь период их накоплений (величины накопленной инфляции) над суммой их прироста. Применяя компьютерную опцию «Подбор параметра», получим n = 25,99 мес. За этот срок удастся накопить:

1 X (1 + 0,05 / 12) 26 + 12 X 0,1 X [(1 + 0,05 / 12) 26 — 1) / 0,05 = 1,114 + 2,740 = 3,58 млн р.

Начиная со следующего месяца суммарные инфляционные потери за весь период накоплений превысят сумму пополнения депозита. Как видно из этого примера, аккумулирование средств на депозите во многом защищает средства от пагубного влияния инфляции, поскольку в силу частичной защиты средств процентами, начисляемыми банками на вклады, кумулятивное воздействие инфляции на сбережения наступает позднее (сравним показатели k ₃ из предыдущего и этого примера –14 и 26 месяцев соответственно). В то же время, как указано ранее, покупательная способность депозита при дальнейшем его пополнении будет продолжать расти вплоть до накопления 0,1/(0,07/12) = 17,14 млн р.

Вопрос 6

Какой должна быть минимальная сумма увеличения накоплений, чтобы аккумулирование средств не отставало от удорожания целевого актива?

Поскольку темп роста цены целевого актива ( V_t ), как указано ранее, ежемесячно составляет i / 12, темп роста средств на депозитах без пополнения ежемесячно составляет R_d / 12, для ответа на вопрос о минимальном рублевом приросте суммы пополняемого депозита ( S ₁) должно соблюдаться следующее условие:

S1 ^ (i X Vt — Rd X STot) / 12, где STot – общая сумма средств на пополняемом и не пополняемом депозитах на момент внесения средств (S1) на пополняемый депозит.

Для недопущения увеличения дефицита между суммой депозитных средств и стоимостью целевого актива необходимо, чтобы темп прироста накоплений на двух депозитах соответствовал следующему условию:

S ₁ / S_Tot ≥ ( i – R_d ) / 12.                                                                            (23)

Если сумма пополнения депозита будет оставаться постоянной, то темп роста средств будет замедляться и в случае превышения уровня роста цен на целевой актив в определенный момент при достижении определенной суммы дальнейшее аккумулирование средств на обоих депозитах начнет отставать от удорожания целевого актива. Такая максимальная сумма может быть определена из следующего выражения:

S TotMax = 12 S 1 / ( i – R d ).                                                                           (24)

Пример 9

Пусть V_t = 8 млн р., S ₀ = 1 млн р., S ₁ = 0,1 млн р./мес., i = 12%/год, R_d = 6%/год.

Из выражения (22) определим минимальную сумму вклада на пополняемом депозите ( S ₁), при которой аккумулирование средств не будет отставать от удорожания цены целевого актива:

S 1 >  (0,12 X 8 — 0,06 X 1) / 12 = 0,075.

То есть минимальная сумма взноса должна составлять 75 тысяч рублей (в примере показан расчет минимальной суммы для самого первого взноса на пополняемый депозит).

Теперь рассчитаем для условий этого примера минимальный темп прироста накоплений на двух депозитах, не допускающий увеличения дефицита денежных средств на целевых депозитах. Используя выражение (23), получим:

S ₁ / S_Tot ≥ (0,12 – 0,06) / 12 = 0,005.

То есть минимальный темп прироста накоплений должен составлять 0,5 процента в месяц (в примере показан расчет минимальной суммы для самого первого взноса на пополняемый депозит).

И наконец, рассчитаем максимальную сумму, которую можно накопить на депозитах (пополняя ежемесячно депозит на одинаковую сумму S ₁) без угрозы для отставания от инфляции. Используя выражение (24), получим:

S TotMax = 12 X 0,1/(0,12 — 0,06) = 20.

То есть эта сумма составляет 20 миллионов рублей, и заемщику при таких условиях не грозит отставание от инфляции, поскольку эта величина намного больше стоимости целевого актива.

Заключение

Автором проведен анализ влияния инфляции на процесс накопления денежных средств при планировании приобретения дорогостоящего имущества и предложены способы, которые позволяют вычислить следующие параметры:

• •    срок, необходимый для накопления требуемой суммы с учетом динамики изменения стоимости целевого актива;

• •    максимальная сумма накопления в текущих ценах в условиях защиты (частичной защиты) от инфляции в форме депозита;

• •    время, по истечении которого перестает расти покупательная способность периодически пополняемого депозита, а также момент, после которого потери от накопленной инфляции сравняются с суммой пополнения накоплений.

Показано наличие двух реперных уровней инфляции, которые необходимо учитывать:

• •    первый, когда накопленная за несколько периодов инфляция сравнивается с величиной (суммой) ежепериодного пополнения депозита;

• •    второй (критический для индивидуума), когда инфляция достигает такого значения, при котором пополнение аккумулированной на депозите суммы в размере ранее осуществлявшихся траншей становится нецелесообразным с экономической точки зрения в силу равенства инфляционного обесценения сумме пополнения депозита.

Также установлено, что с превышением уровня инфляции определенной величины снижается продолжительность периода достижения суммы, накопление свыше которой теряет практическую целесообразность.

Продемонстрирован способ оценки минимальной суммы увеличения накоплений, гарантирующей, что аккумулирование средств не будет отставать от удорожания целевого актива.

М. : Дело Лтд, 1995. 320 с.

Обсуждение темы, поднятой автором статьи, будет продолжено в следующем номере журнала.

***

^^^\ ^" ^^ ^^ Единый ВЕРХОВНЫЙ СУД: СОБСТВЕННИКИ НЕ ОБЯЗАНЫ (    ^ У * ресурс НАПРАВЛЯТЬ ИСПОЛНИТЕЛЮ КОММУНАЛЬНОЙ

I %^ застройщиков УСЛУГИ СВИДЕТЕЛЬСТВО О ПОВЕРКЕ

Верховный Суд РФ определением от 01.09.2022 по делу №АПЛ22-283 признал недействующим пп. «д» п. 34 «Правил предоставления коммунальных услуг собственникам и пользователям помещений в многоквартирных домах и жилых домов», утвержденных Постановлением Правительства РФ №354 от 06.05.2011 (Правила), в части, предусматривающей обязанность потребителя коммунальных услуг направлять их исполнителю копию свидетельства о поверке или иного документа, удостоверяющего результаты поверки прибора учета.

Гражданин обратился в ВС с административным исковым заявлением о признании недействующим пп. «д» п. 34 Правил в части, предусматривающей обязанность потребителя коммунальных услуг представлять их исполнителю для подтверждения факта поверки прибора учета копию свидетельства о поверке или иного документа, удостоверяющего результаты поверки прибора учета, осуществленной в соответствии с положениями законодательства РФ об обеспечении единства измерений. Нарушение своих прав истец усматривал в том, что в мае 2021 он провел поверку установленного в принадлежащей ему квартире индивидуального прибора учета – счетчика горячей воды. Однако исполнитель коммунальных услуг ГБУ «Жилищник Останкинского района» отказался признать факт поверки на основании сведений, содержащихся в Федеральном информационном фонде по обеспечению единства измерений (ФГИС «АРШИН»), и потребовал представления свидетельства о поверке прибора учета.

Окончание на с. 72