Asymptotic estimate of a Petrov - Galerkin method for nonlinear operator-differential equation

Galerkin methods are widely used in various stages of mathematical modeling. These methods are used for study of the correctness of the mathematical model and the development of the approximate algorithms (see [1, 2], etc). One of these methods is the Petrov - Galerkin method. It is based on the use of two basises. The approximate solutions are constructed by the first basis, while the residual must be orthogonal to the second basis (see [3]). Petrov - Galerkin method was used in [4, 5] for the numerical solution of stationary models. This method has been investigated in [2, 6, 7] for parabolic mathematical models with a dominant convection.

When the two basises are linked through a linear operator, Petrov - Galerkin method is called the moments method. The analysis of the moments method applied to the linear ordinary differential ecpiations was given in [8, 9]. A.V. Dzishkariani [10] used this method in the construction of projection-iterative method for linear elliptic boundary value problems. A.G. Zarubin [11] studied the same method for quasilinear stationary operator equations in Hilbert space. In [12, 13] the moments method was used to approximate determination of eigenvalues for various classes of operator ecpiations. In given papers the convergence of approximate solutions was established and the convergence rate was obtained.

The study of nonlinear mathematical models is one of the difficult problems. The investigation of the differential equations in operator form is of special interest. The

Galerkin method for nonlinear differential-operator equations was studied in [14-16], where eigenvectors of the operator similar to the leading operator A of the equation were used as the basis functions. However, in specific mathematical models it is not always possible to find the explicit form of eigenvectors. In this paper, with the help of the moments method the approximate solution of the Cauchy problem for operator-differential equation is constructed in separable Hilbert space H. In contrast to [14-16] here the basis elements are not eigenvectors of a similar operator, which significantly expands the class of problems. In these papers a leading operator A and similar operator B satisfy the acute-angle inequality. In the present paper, this limitation is removed. New asymptotic estimates for the convergence rate of approximate solutions are obtained in uniform topology. The results are illustrated by the initial-boundary value problem for a nonlinear parabolic ecpiation.

1. Statement of the Problem and Auxiliary Assertions

Let H 1 be separable Hilbert space densely and compactly embedded in a separable Hilbert space H with norm || • || _H = || • | | and iniiei’ product ( ■, • ) .

In the space H, we consider the Cauchy problem

u ( t ) + Au ( t ) + K ( u ( t )) = h ( t ) , u (0) = 0 ,

where u ( t ) is the unknoта function, h ( t ) is a given functkm. The functions u ( t ) aiid h ( t ) are determined on [0 , T ] ( T <  to ) . In the sequel, we assume that the operators A and K satisfy the following conditions:

(i) A is self-adjoint positive definite operator in H with the domain D ( A ) = H 1 .

(n) The operator K is subordinate to operator A with order a ; i.e.. D ( K ) D D ( A ) and for any element v from H 1 , the inequality

|K ( v ) ||< Ф ( |A 1 / 2 v| 2 ) »Av« " , 0 < a< 1

holds, were ф ( £ ) is the nondecreasing continuous positive function on [0 , to ) . (iii) The nonlinear operator K is monotone.

Let us define some spaces that will be necessary further.

Let L 2 (0 ,T ; H ) be a. finite norm

Hilbert space of all strongly measurable functions on [0 , T ] with

T

Consider the ftmctions ^J ||Au ( t ) | |² dt^ <  to.

u ( t ) (0 < t < T ) with vttines in H 1 and with norm

Let the functions u ( t ) have derivatives u ' ( t ) G L 2(0 , T ; H ) in

the sense of distributions. Equip the set of these functions with the norm

1Ы112=

T

(/( flu ' ( t ) fl ² + 0

fl Au ( t ) fl ²) dt )² .

The completion of this set with respect to this norm is a Hilbert space W 1 ( H,H 1 ) .

Introduce the subspace W₂1 ( H,H 1) = {u ( t ) G W 21( H, H 1) ,u (0) = 0 }. О

The solution of problem (1) is defined as a function u ( t ) GW 2¹ ( H,H 1) that satisfies (1) for almost all t.

Condition (i) implies that the operator A has an inverse A ¹ : H ^ H 1 .

Futher, the following Bihary result (see [17]) will be necessary for us.

Lemma 1. Let g ( s ) be a positive function for s >  0 and let k,m >  0 . Then from the inequality

t

u ( t ) < k + m j v ( s ) g ( u ( s )) ds, a < t < b

a

it follows that

t u (t) < G-1 ^G (k) + mJ v (s) ds^ ,

a where G (u) = J d), u>u о > 0.

u 0

Theorem 1. Suppose that h ( t ) G L 2(0 ,T ; H ) , the operator K is compact in L 2(0 ,T ; H ) .

О

Then (1) has a unique: solution in W1 ( H,H1 ) .

Proof. It is known (see [18]) that the problem v' (t) + Av (t) = g (t), v (0) = 0

О with g(t) G L2(0, T; H) lias a, uniqire solution v(t) GW21 (H,H 1); moreover.

T

T j Bg(t)II2dt, 0

j ( lv' ( t ) В ² + BAv ( t ) В 2) dt < M 0

where the positive constant M is independent of t. From (3) it follows that the linear operator

(d + A)'

О

: L 2(0 ,T ; H ) W1 ( H,H 1)

exists and it is bounded. Make a replacement (f + A) u(t) = v(t) in (1). Then we obtain a functional ecpiation v (t) + K

= ^{h (} t )

with the compact operator K ^( ft + A ) 1^ in L 2(0 ,T ; H ) . We shall use the Leray -

Schauder principle. Consider the family of ecpiations u'(t) + Au(t) + XK(u(t)) = Xh(t), u(0) = 0, 0 < X < 1.

Let u ( X,t ) be the solution of (4) . By M i denote various positive constants independent of A and t.

Take the inner product of equation (4) bу Au ( X, t ) and integrate the resulting relation over the interval [0 , t ] , t < T. By applying inequality (2) and i -inequality, we come to the estimate

t

2 «A ¹ / ² u ( X,t ) fl ² + у «Au ( X,? ) fl ² d? <  У «А ( t ) fl 2 , 2 + 0

t

t

| У «Au ( a,? ) « ² d? + У «Au ( X,? ) « ^{1+ а} ф ( «A ¹ 1 ² u ( X,? ) « ² ) d?

Using Holder inequality, we get

.

t

2 «A ¹ / ² u ( X,t ) | |² + у «Au ( A,? ) « ² d? <  0

t

У «А ( t ) « 2 , 2 + | У «Au ( a,? ) « ² d? +

1+α t                    \ 2

j « Au ( A,? ) «² d? I

.0                      /

1-α t                                 \ 2

jф 1^ ( «A ¹ / ² u ( X,? ) « ² ) d? I .0                                   /

Further, the Young inequality:

ab <  y i ⁵ a ⁵ +     1

δδ

-δ δ i г-1 bs-1, a,b,i> 0, 5> 1

is applied to the right-hand side of the preceding relation. Let 5 = a +1 • Choosing sufficiently small i >  0 , we have

«A ¹ / ² u ( X,t ) « ² < M 1

t

1+ A 12 a ( «A ¹ / ² u ( X,? ) « 2 ) d?

By using Lemma 1, we obtain

sup «A ¹ / ² u ( X,t ) « < M 2 .                                (5)

0

From (2) and (3) we have

«u ( X,t ) « 1 , 2 < M 3    «А ( t ) « 0 , 2 +

T                                               \ ¹ / ²

У «Au ( X,t ) « ² ” ф ² ( «A ¹ / ² u ( X,t ) « 2 ) dt I 0

By using the last inequality and (5) , we get

^u ( X,t ) У 1 , 2 < M 4

\\h ⁽ t ) I I 0 , 2 +

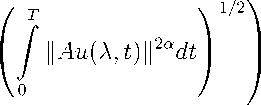
Since 0 < a <  1 , then

\u ( X,t ) У 1 , 2 < M 5

Thus, problem (1), according to the Leray - Schauder principle, has at least one solution О

u ( t ) gW ₂ ( H,H 1 ) . Since the operator K ( ■ ) is monotone, the solution is unique. The proof of theorem is complete.

□

• 2.    Petrov - Galerkin Method

Let {e _s } “1 be a complete orthogonal system of elements in H. The sequence ф _s G H 1 ( s = 1 , 2 ,... ) is determined 1.>y the equation Aф _s = e _s .

Let P n be the orthogonal projection in H onto the linear span H n of the elements e 1 , e 2 , . . . , e n .

If F : H ^ H is a linear bounded operator, we have an operator norm

\F \ h ^ h = sup \Fx\, x G H.

\\x\\ =1

Let g ( n ) = A 1( I — P _n ) \ _H^_H . The operator A ¹ is compact operator in H, therefore, the function g ( n ) exists, moreover than g ( n ) ^ 0 as n ^ to. In many cases the function g ( n ) is accurately calculated or estimated from above by the function which tends to zero as n ^ to.

The function g ( n ) is the main characteristics of the convergence rate of approximate solutions found by the moments method. The moments method for the approximate solution of the problem (1) leads to the following ecpiation:

Pnun(t) + Aun(t) + PnK(Un(t)) = Pnh(t), Un(0) = 0,(6)

where u n ( t ) = ^ n =1 a s ( t ) ф ₈ .

From now on. by C we denote various positive constants independent of n and t.

Lemma 2. Suppose that h(t) G L2(0, T; H). Then the inequalities sup || A1 /2Un | < C,(T)

0

|Aun|0,2 < c(8)

hold.

Proof. Let us multiply (6) by Aun in the sense of the inner product in H and then integrate from 0 to f < T. By using the е -inequality, we come to the relation

ξξ

J ( P „ u n ,Au „ ) dt + J ||Au „ \ |² di <

ξξ

; H * H 2 , 2 + ; I H AU nH² dt ₊ 1 I W K ( U n ) ц² dt.

Now we transform the first term on the left-hand side of (9):

ξ

j ⁽ P n ^U _n , A ^U n

ξ

) dt = I

( U n , Au _n ) dt.

Since u ' ( t ) G H 1 and condition (i) holds,

ξ

I ( P n U n Au_n ) dt = 0

ξ

У ( A ¹ / ² U n , A ¹ / ² U n ) dt 0

ξ

W d । A ^{1 / 2} U n 1 2 dt =

= 1I A ¹ /² U n ( e )| 2 - 1 I A ¹ / ² U n (0)1 2 = 1 I A ¹ /² u „ ( Ц )| ² .

By applying (2) to the last term on the right-hand side of (9), using the Young inequality, we obtain

ξξ

II A ¹ / ² U n ( e )|| 2 + I H AU nH ² dt <  C ( U N ² , 2 + IФ ² / ^{(1 -a} ) (l| A ¹ / ² U nI I 2 ) dt ^j •      (¹⁰)

By using Lemma 1, we obtain

ξ

+ CI dt^, b

ha ¹ / ² U n ( e ) в ² <  g ^{- 1} ( g ( с h* ( t ) в 2 , 2 )

z where G(z) = J ф2/f—)(t), z > z2 > 0• The existence of the function G- 1(z) follows from z 0

the positiveness and continuity of the function ф ( e ) • Thus, estimate (7) is proved. Next, from (10) and (7) we obtain (8). The proof of lemma is complete.

□

We consider the problem

PnVn (t) + Avn (t) + PnK‘ (Un (t))Vn (t) = Pn*(t), Vn (0) = 0•(11)

Lemma 3. Suppose that h ( t ) G L ₂ (0 , T ; H ) , *‘ ( t ) G L ₂ (0 , T ; H ) , * (0) = 0 and for any v G H 1 the. inequality

|K‘(z(t))v|< ф 1(ha 1 /2zH)HAvH'Hv| 1-Y, 0 < Y< 1

holds, where. K ‘ is the. FreehL't derivative, ф 1 ( e ) is a continuous positive function on [0; to ) • Then v _n ( t ) = U ‘_n ( t ) .

Proof. Differentiate (6) with respect to t. Then

PnUf (t) + AUn (t) + PnK‘(Un(t))Un (t) = Pnh’(t), Un (0) = 0, PnUn (0) = 0•(13)

Take the inner product of the equality P nu'n (0) = 0 bу Au n (0)

0 = ( P n u n (0) A n (0)) = BA ¹ / ² u n (0) В ² .

Hence,

Bu n (0) В = 0 .

From (11) and (13) it follows that

P n ( v n ( t ) — <  ( t )) + A ( V n ( t ) — u n ( t )) + P n K ‘ ( U n ( t ))( V n ( t ) — u n ( t )) = 0 .      (14)

Take the inner product of (14) by A ( v n — u ‘_n ) and integrate the resulting relation over the interval [0 , e ] , e < T. Then

ξξ

2 BA 1 / 2 ( v n ( e ) — u n ( e )) В ² + У BA ( v n — u n ) B ² dt < j BK‘ ( u n )( v n — u n ) BBA ( v n — u n ) Bdt.

From this, together with (12) and (7), we have

ξ

2 BA ¹ / ² ( v n ( e ) — u n ( e )) В ² + У BA ( v n — u n ) В ² dt <

ξ

< CI BA ( V n — u ’n ) В ^{1+ Y} Bv n — ¹ - ^Y dt.

By applying the Young inequality, we obtain

ξξ

BA ¹ / ² ( v „ ( e ) — u n ( e )) B ² + У BA ( v n — u n ) В 2 dt < Cj Bv n — u n B 2 dt.

By using the fact that A is a positive definite operator, we obtain

ξξ

I Bv n — u n B ² dt < CI BA ¹ / 2 ( V n — u n ) В ² dt.

Thus,

ξ ba ¹ / ² ( vn ( e ) —un ( e )) b ² < cj ba ¹ / ² ( vn — un ) b ² dt. 0

Further, using the Gronwall inequality, we obtain v_n ( t ) = u'_n ( t ) . The proof of lemma is complete.                                                                         ^

Lemma 4. Let the assumptions of Lemma 3 hold. Then

∥ u^′ _n ∥ 0 , 2 ≤ C.

Proof. Take the inner product of (11) by Avn and integrate the resulting relation over the interval [0 , С ] , С < T. Then

ξ

T

Hh ' ll 0,2 + / 0

BK ‘ ( U n ) V n B ² dt

2 BA ¹ / ² v n ( С ) B ² + У BAV n B ² dt < C

From the last inequality, by using (12) and estimates (7) and (8), we obtain sup В A ¹ / ² v n B < C,

0 ≤t≤T

∥ Av_n ∥ _{0 , 2} ≤ C.

Next, using Lemma 3, we obtain (15). The proof of lemma is complete.

□

Theorem 2. Let the assumptions of Lemma 3 hold. Then sup Bun - uB < Cg1 /2(n),                             (16)

0 ≤t≤T

BA ¹ / ²( U n - U ) В 0 , 2 < Cg ¹ / ²( n ) .                              (17)

Proof. For the solutions of problems (1) and (6) we have

( U - U n ) ‘ + A ( U - U n ) + K ( U ) - K ( U n ) = ( P n - I )( и П - h + K ( U n )) .

Let us multiply this equation by и - u _n in the sense of the inner product in H and then integrate from 0 to С < T. By using the monotonicity of the operator K, we come to the relation

2 Bu ( С )

^{- U} n ⁽ С ) I I 2 +

ξ

I BA ¹ / ²( и - U n ) B ² dt <

ξ

У | (( P n - I )( U ’n - h + K ( U n )) ,u - U n ) Idt. 0

Since и - u _n E H 1 , we have

ξ

ξ

∥ u^′ n

^- h + ^{K ( U} n ) ^{BB (} P n ^- I ^{)( U - U} n ) ^Bd t.

2 ^{Bu (} < ) ^{- U} n ⁽ < ) ^{B 2} + I ^B A ¹ / ^{2( U - U} n ) ^{B 2 d} t <

Since

B ( P n - I )( и - U n ) B = B ( P n -1 ) A — ¹ / ² A ¹ / 2 ( и - U n ) B = B ( P n -1 ) A^{- 1} / ² B h ^ h BA ¹ / ²( U - U n ) B =

= BA-1 /2(Pn -1)Bh^hBA1 /2(и - Un)B < g1 /2(n)BA1 /2(и - Un)B, then

2 \\u ( е )

^^^^^^^^^r

u n ( е ) и ² +

ξ j «л1 /2(u

^^^^^^^^^r

U n ) | |² dt < g ¹ //

ξ

⁽ nnj

11 U n - h + K ( U n ) ||A ¹ / ²( и - U n ) ||dt.

Next, applying E -inequality and choosing sufficiently small e >  0 , we come to the inequality

T

«U ( ( ) - U n ( ( ) | ² + J «л 1 / ²( U - U n ) « ² dt < C ( |h| 02 + «< « 02 + K ( U n ) « 02 ) g ( n ) . 0

From (2) and (15) we obtain (16) and (17) . The proof of the theorem is complete.

□

• 3.    Application to Initial-Boundary Value Problems

In this section, the projection method is applied to a nonlinear parabolic equation with discontinuous boundary conditions.

Let Q = [0 , 1] x [0 , 1] , Q = Q x [0 , T ] . In Q, consider the following initial-boundary value problem:

ди ( x 1 , x ₂ , t ) ∂t

+ A² U ( x 1 ,x 2 ,t ) + U ( x 1 ,x 2 ,t ) |u ( x 1 ,x 2 ,t ) | ^ = h ( x 1 ,x 2 ,t ) ,

( x 1 ,x 2 ,t ) G Q, (18)

^ul d Q = ⁰ ,

и ( x 1 , x 2 , 0) = 0 , ( x 1 , x 2 ) G Q , ди (0 , x ₂ , t )      ди (1 , x ₂ , t )      д ² и ( x 1 , 0 , t )      д ² и ( x 1 , 1 , t )

∂ν

∂ν

∂ν ²

∂ν ²

= 0 ,      (20)

where p >  1 , v is external normal to д Q . о

о

Let H = L ₂(Q) , H 1 = W 2 (Q) , where W 2 (Q) = {n ( x 1 ,x ₂) G W 24 (Q) ,v ( x 1 ,x ₂) | d _Q =

0 ,

dv (0 ,x 2 )   dv (1 ,x 2 )   d ² v ( x 1 , 0)    d ² v ( x 1 , 1)

∂ν

∂ν

∂ν ²

∂ν ²

= 0 }, W ₂⁴(Q) is the Sobolev space (see [19]).

611 H 1 define the operators Л = A² arid K = ( I• ) |I • | ^p .

It is known that the system of the functions e kj ( x 1 , x ₂) = sin knx 1 sin jnx ₂ , ( k = 1 , 2 ,... ,j = 1 , 2 ,... ) is a complete ortllogonal system in L ₂(Q) . Let P _n Ire the orthogonal projection in L ₂(Q) onto the 1 inear span Hⁿ of the frinctions {e kj ( x 1 , x ₂) } nj =1 . о

The functions ф _kj ( x 1 , x ₂) GW 2 (Q) are the solution of the equation

A² ф kj ( x 1 ,x 2 ) = e kj ( x 1 ,x 2 ) .

From the form of functions ф _kj ( x 1 , x ₂) , we obtain

g ( n )= « (A²) - ¹ ( I - P n ) « _t 2 ( _O ) ^ l ,_№ < C 3 .

The approximate solution for (18) - (20) is defined as

n

Un (x 1 ,x2 ,t) = y^ akj (t) фkj (x 1 ,x2), k j=1

where the unknown functions a kj ( t ) are the exact solution of the Cauchy problem

P n u n ^{+ A} u n ⁺ P n u n Bu n W    P n h, u n ^{( x} 1 , ^x 2 , ^{0)   0} *

Let us check inequality (2) *

By using the embedding of the space W 24 (Q) in to C ²(fi) , we obtain

I K ( v ) B l 2(a) = Bv|v| ' B l 2< C|Mg“.                       (21)

Since llvllc (Q) < C v X((Q , HvHc (Q) < CIIA v|L 2(Q) = C || Л 1 / 2 vBL 2(q) *

From (22) it follows that

∥ v|v| ^ρ ∥ L 2 (Ω) ≤C ∥ A ^{1 / 2} v ∥ ^ρ L ⁺ ( ¹ Ω) .

Thus. (2) hole Is if a = 0 *

Let us check inequality (12) * Write down the Frechet derivative of the operator K :

K ‘ ( z ( x 1 ,x 2 , t )) v ( x 1 ,x 2 ) = (1 + p ) |z ( x 1 ,x 2 , t ) l ^p v ( X 1 ,X 2 ) *

Next,

IK ‘ ( z ) v| l 2 (Q) <  (1+ p ) ||zH ^ (Q) BvB l 2 (Q) < C В A zII L 2 (Q) BvB l 2 (Q) *

Hence. (12) hokIs if 7 = 0 *

Let h(x 1, x2, t) G L2(Q) and h(x 1, x2, 0) = 0* Then from Theorem 2 it follows that sup Bun(x 1 ,x2,t) - u(x 1 ,x2,t) Bl2(Q) < Cn3/2,                   (22)

0 ≤t≤T

В A( U n ( x 1 , x 2 ,t ) - u ( x 1 ,x 2 ,t )) || _l 2 ( _Q ) < Cn - ³ / ² *

The numerical realization of the Petrov - Galerkin method for (18) - (20) is made using the Matlab software package. The implementation of this algorithm in the form of a computer program allows to verify (22). The input data for the program are: the function f ( x 1 , x ₂ , t ) and the value of p . For testing of the algorithm, we put p = 1. T = 1. We cLoose h ( x 1 , x ₂ , t ) so that the exact soli.ition of (18) - (20) is u ( x 1 , x ₂ , t ) = t ² ( x 1 — x 1) ³ ( x 22 — x ₂ ) ³. The program finds an approximate solution and compares it with the known exact solution. Table 1 presents the results of numerical experiments containing sup Bu n ( x 1 ,x ₂ , t ) — u ( x 1 , x ₂ , t )|| _{l 2} (q) for different values of n. The results of numerical 0 ≤t≤T experiments are consistent with the theoretical estimate.

Table

n = 10	n = 15	n = 20	n = 25	n = 30	n = 35
0 , 253 • 10 - 6	0 , 153 • 10 - 7	0 , 107 • 10 - 7	0 , 793 • 10 - 8	0 , 511 • 10 - 8	0 , 411 • 10 - 8