Automated Analog Circuit Design Synthesis Using A Hybrid Genetic Algorithm with Hyper-Mutation and Elitist Strategies

Published Online October 2009 in MECS

Analog circuits are of great importance in electronic system design since the world is fundamentally analog in nature [1]. During the last decade, advances made in integrated circuits (IC) have greatly increased the scale and analog IC design complexity. Therefore, analog circuit design automation techniques become essential to obtain solutions that satisfy the requested performance with the minimum time effort [2].

Scientists have proposed many methods for analog circuit design automation during past decades. These methods incorporated heuristics [9], knowledge bases [10], and simulated annealing [11]. Efforts using techniques form evolutionary computation have appeared over the last decade. Lohn, et al. [1] propose a linear representation method to analog circuits. They use the

Manuscript received January 13, 2009; revised June 21, 2009; accepted July 21, 2009.

circuit-constructing instruction sets, which can be translated to analog circuits, as the chromosomes, and use the genetic algorithm (GA) to evolve these chromosomes. Koza, et al. [3] represent the analog circuits as circuitconstructing program trees, and use genetic programming (GP) system to evolve these program trees. Both Lohn and Koza’s methods can simultaneously evolve the topology and the component values of the circuits with minimal primary knowledge. Wang, et al. [4] expand Koza’s method and propose an automated analog circuit design method using two-layer genetic programming. Divide-and-conquer strategy is used in their method. Nicosia, et al. [5] used multi-objective optimization method to evolve analog circuits with both accurate and robust characteristics. Das and Vemuri [12] proposed an automated passive analog circuit synthesis framework. The circuit representing method is similar to Loha’s method. They also use GA as the evolving engine.

Scientists’ work shows that evolutionary methods bring great advantage in analog circuit design automation. However, there were hardly any discussion on the relationship between the analog circuit’s topology and the component’s value, or in other words, the trade-off between the evolving of the analog circuit’s topology and the evolving of the analog circuit’s component values.

Lohn’s and Das’s works show that, GA is an efficient way of automated analog circuit design. In GA based automated analog circuit design, crossover is used to evolve the circuit’s topology, and mutation is used to evolve the circuit’s components values. GA’s inherent characteristics are high crossover (0.6~1.0) rate and low mutation rate (0.001~0.1) [6]. The traditional view is that crossover is the more important of the two techniques (crossover and mutation) for rapidly exploring a search space [13]. Topology and components values are both important to analog circuit design. Thus, traditional GA is not very effective in evolving circuit’s components’ values. Analog circuit’s components values design is as important as Analog circuit’s topology. For instance, with the same topology, different component values will endow the filter circuits with different frequency characteristics. So, it is very important to cover the shortage of traditional GA on automated analog circuit design. A natural idea is to increase the mutation rate.

Considering the shortage of traditional GA on automated analog circuit design, this paper proposes a novel GA with hyper-mutation and elitist strategies which is specialized for analog circuit design automation. The hyper-mutation strategy is used to increase the mutation rate of the circuit’s components values. So, the hypermutation strategy enhances GA’s ability on evolving circuit component’s values. The elitist strategy is used to keep good solutions and to help guide the hyper-mutation search to the more fruitful regions of the solution space [7]. Experiments show that, the proposed algorithm is more efficient than traditional GA on analog circuit design.

• II.    Preliminaries

This section introduces some preliminary information for our paper. There are three subsections in this part. 1) The brief description of the circuit representation method used in this paper. 2) The preliminary experiment and discussion of traditional GA on analog circuit evolving. 3) The preliminary experiment and discussion of GA with hyper-mutation on analog circuit evolving.

• A.    Brief Description of the Circuit Representation Method Used in This Paper

  Since we use Lohn’s linear encoding as our analog circuit representation method, it is necessary to give it a brief introduction. In Lohn’s circuit representation method, circuit designs are constructed by an automation that is programmed via a set of cc-bot instructions [1] that are sequentially performed. Each cc-bot instruction contains several elements, the component type, component value and the instruction to place the component. The component type can be R (resistor), C (capacitor), L (inductor), or transistor. R, C and L are dual-port components. Though a transistor is a three-port component, its connection methods are reduced to fifty-two frequently used conditions so that the transistor can be used as a dual-port component. The component value uses three bytes. That allows the component values to take on one of 256³ values. t he value of the transistor indicates its connecting condition. There are five instructions used to place the components: x-move-to-new, x-cast-to-previous, x-cast-to-ground, x-cast-to-input, x-cast-to-output. The meanings of each instruction are summarized in TABLE I.

The circuit is constructed by the cc-bot inside of a template circuit. The template circuit defines the input and output terminals. An example template circuit is shown in Figure 1. An ideal voltage source Vs is connected to ground and to a source resistor Rs. The circuit’s output voltage is taken across a load resistor Rl. The lists of cc-bot instructions manipulated by the GA are variable-length lists so that the size of the circuit can be evolved. When the cc-bot reaches the last component to place in the circuit, the last active node is connected to the output terminal by a wire (accomplished by connection of a 1 resistor), so that unconnected branches can be eliminated. In circuit simulation step, the cc-bot instruction set and the template circuit are translated into circuit netlist and simulated by SPICE (It is a kind of circuit simulation tool).

TABLE I.

Summary of Circuit-placing Instructions in Current System. x Denotes the Component Type: Resistor, Capacitor, Inductor, or Transistor Configuration [1].

Instruction	Outgoing Node	Active Node
x-move-to-new	newly-created node	becomes the newly-created node
x-cast-to-previous	previous node	unchanged
x-cast-to-ground	ground node	unchanged
x-cast-to-input	input node	unchanged
x-cast-to-output	output node	unchanged

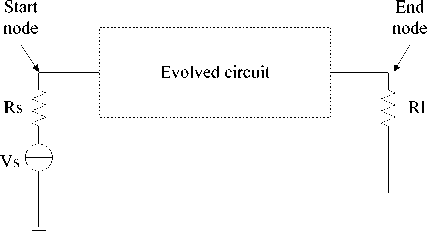
Figure 1. An example template circuit with one ideal voltage source and a load resistor.

• B.    Preliminary Discussion of Traditional GA on Analog Circuit Evolving

Genetic algorithm was initially introduced by John Holland [14]. It has been developed dramatically during the recent decades. Genetic algorithm constitutes a class of search methods especially suited for solving complex optimization problems [13] [15] 16] [17] [18] and useful for computer aided design [19] [20]. Analog circuit design automation is a typical computer aided design problem. Lohn [1] and Das [12] have proved that, GA can bring significant advantage in Analog circuit design automation. Though method used in Koza’s work [3] is GP, The only difference between GP and GA is the different data structures they use (GP use tree structure, and GA use binary or real encoding strings as its chromosome). So, GP can also be classified as a member of GA family.

Though previous works proved GA’s ability in analog circuit design automation, traditional GA still has the potential to be improved so that it would be more suited for analog circuit design. Analog circuit design involves circuit topology design and component values design. For an analog circuit only consists of resistors, capacitors and inductors, the total topology possibility can be calculated by the following equations. Let n denotes the component numbers used in an analog circuit consists of resistors, capacitors and inductors, and f (n) denotes the total topology-possibilities of the n-component circuit. If a new component is added to the circuit, the newly added component and the circuit should be in series or in parallel, and the component can also be resistor, capacitor or inductor. So, the total possibilities of the (n+1)-component circuit can be expressed as 6 • f (n) . It is obvious that f (1) = 3 . For there are only three possibilities: the only component can be resistor, capacitor or inductor. The formula of f (n) is shown in equation (1).

<

f ( П + 1) = 6 • f ( n )

n >  1

I f (1) = 3

^

f ( n ) = 3 X 6 ^{n - 1} n >  1

Let p ( n ) denotes the total component-value possibilities of an n -component circuit. Then p ( n ) can be approximately calculated by equation (2).

p ( n ) = 256^{3 n} n >  1 . (2)

It can be inferred from equation (1) and (2) that: the search space of the component value is much larger than the search space of the circuit topology. However, traditional GA is more efficient in evolving analog circuits’ topology due to its high crossover rate (0.6~1.0) and low mutation rate (0.001~0.1) [6] (crossover evolves circuit topology and mutation evolves component value). Since low mutation rate cause traditional GA’s lack of evolving circuits’ component value, a natural idea to supply this gap is to simply increase GA’s mutation rate. The following subsection is going to discuss whether this idea makes sense.

• C.    Preliminary Experiment and Discussion of GA with Hyper-mutation on Analog Circuit Evolution

It is mentioned that, a natural idea to supply this gap is to simply increase GA’s mutation rate. In fact, there have already been many researches on GA’s mutation rate and mutation strategies. The method of increasing GA’s mutation rate is called hyper-mutation. Hyper-mutation has been used for keeping the solutions’ diversity of GA having continuous and time-dependent non-stationary Environments by Cobb [8]. Cobb simply performs the hyper-mutation by increasing the mutation rate from 0.1% to 50%. Jin, et al. [21] introduced hyper mutation to the basic clonal selection algorithm model in order to overcome premature convergence and stagnation at the end stage of iterative optimization. The hyper mutation used in is also called gene mutation in that paper. It is used to help making the antibody escape from local optima. Falco, et al. [22] proposed a mutation-based genetic algorithm. The search mechanism used in their algorithm is mutation only.

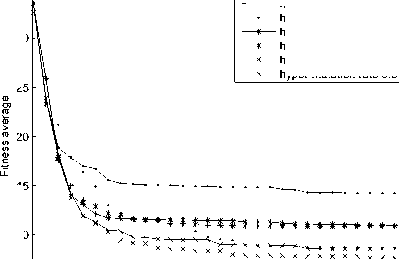
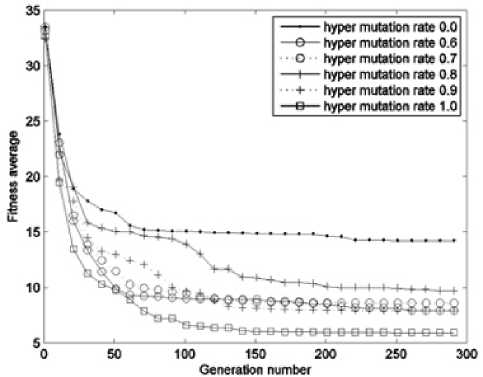
Since analog circuit design consists of topology design and component value design, the crossover mechanism and mutation mechanism are both need under current circuit-representation method. We perform hypermutation method by simply adding a hyper-mutation procedure after the crossover and mutation operations. In hyper-mutation procedure, we gradually increase the hyper-mutation rate from 0.1 to 1.0 (increased by 0.1), and observe the hyper-mutation mechanism’s performance by performing a low-pass filter experiment. The amplitude-frequency characteristics results and the fitness curves of the tradition GA and hyper-mutation GA are shown in Figure 3 to Figure 5.

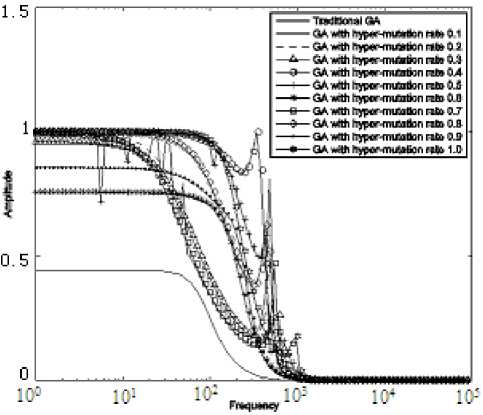
Figure 3. The amplitude-frequency characteristics results of traditional GA and hyper-mutation GA. The experiment is to evolve a low-

hyper mutation rate 0.0 hyper mutation rate 0.1 hyper mutation rate 0.2 hyper mutation rate 0.3 hyper mutation rate 0.4 hyper mutation rate 0.5

100       150       200

Generation number

• Fi gure 4. Fitness curves of the hyper-mutation GA and simple GA. The hyper-mutation rates are 0.1~0.5.

It can be inferred from the amplitude-frequency characteristics results and the fitness curves that, after adding hyper-mutation mechanism, the performance of GA on evolving analog circuit increased significantly. The best fitness is obtained by the proposed algorithm with hyper-mutation rate of 1.0. However, the increasing of the hyper-mutation rate does not always bring better performance. For instance, the results of GA with hypermutation rate of 0.4, 0.5 and 0.6 are all better than the result of GA with hyper-mutation of 0.8. Mutation is a random search strategy. From the experimental results we

• Fi gure 5. Fitness curves of the hyper-mutation GA and simple GA. The hyper-mutation rates are 0.6~1.0.

can see that, it is hard to decide which hyper-mutation rate should be the best since there is not a clear relation between the hyper-mutation rate and the performance. Though hyper-mutation mechanism is useful to enhance GA’s performance in evolving analog circuits, it still need a guide to make it more intent (not completely random) and effective. On this purpose, we try to introduce another mechanism called elitist.

Elitist strategy is useful in helping guide the stochastic search. Deb, et al [22] used elitist archive strategy (it is also called non-dominate sort) to maintain high quality solutions. Venkartaman, et al. [23] used the local elitist strategy among a pair of parents and offspring to increase the convergence of GA. Chu, et al. [24] used elitist nondominated sorting genetic algorithm to optimize RF IC. Former researches show that, elitist strategy can enhance the convergence of evolutionary algorithms. So, this paper introduces hyper-mutation strategy and elitist strategy to traditional GA, and proposes a hybrid GA called HME-GA (hybrid GA with hyper-mutation and elitist strategies). The details of the algorithm are specified in the next section.

III.    Hybrid GA with Hyper-mutation and Elitist Strategies

This section specifies the proposed algorithm HME-GA. The first and second subsections introduce the hyper-mutation and elitist strategies used in the algorithm, and the third subsection gives the integrated architecture of the proposed algorithm.

• A.    Hyper-mutation Strategy

The hyper-mutation is separated from simple mutation. That means the proposed algorithm performs both the simple mutation operation and the hyper-mutation operation. The hyper-mutation operation is performed by randomly choosing some individuals (cc-bot instruction) and randomly changing several components’ values in the chosen individuals. The hyper-mutation operation can only select individuals that are provided by elitist operation. Let p_hm denotes the hyper-mutation rate and

N denotes the population number in the algorithm. Then, the estimate of the hyper-mutation number E [ n ( p_hm )] can be defined by equation (3).

^{E [} n ⁽ P hm ^)] = P hm • ^N .          (3)

Each hyper-mutation operation is followed by a solution-evaluating operation. So, the estimated number of solution-evaluation E [ n_e ] can be defined by equation (4).

E [ П е ] = 2 E [ n(P c )] + E [ n ( P m )] + E [ n ( P hm )]

• ^{e                c               m                m} . (4)

= 2 E [ n ( P c )] + E [ n ( P m )] + P hm . N

E [ n ( p_c )] is the estimated number of the crossover and E [ n ( p_m )] is the estimated number of the simple mutation. It can be easily inferred from function (2) that the estimated number of solution-evaluation increases linearly with hyper-mutation rate p_hm .

• B.    Elitist Strategy

Appropriate topology of an analog circuit is basic so that makes the analog circuit accord with the design request. So, evolving the components values of circuits with better topologies will be more efficient than equiprobably evolving all the circuits in the population. Elitist strategy is used to guide the hyper-mutation search to the circuits with better topologies in the population.

To perform the elitist strategy, we need to establish the elitist set. Generally, the analog circuits with better topologies are more likely to gain better fitness. So the elitist set of the population is composed of individuals with better fitness and fewer components than other individuals in the group. To design elitist strategy in the algorithm, we propose the following assumption: Under randomly generating components’ values, circuits with better topologies will be more capable to gain better fitness than circuits with inferior topologies. The elitist set is gathered based upon this assumption. Circuits with inferior topologies also have the chance to gain better fitness than circuits with superior topologies, so the size of the elitist set should be chosen carefully. On the one hand, the elitist set should be large enough so that it will contain enough superior topology circuits. On the other hand, larger the elitist set is, less guiding-ability it provides to the hyper-mutation operation.

Let Se denotes the elitist set of the population and pe denotes the percentage of the circuits belonging to Se . The size of the elitist set N(Se ) equals n • Pe . n is the population size. The elitist set Se is composed of circuits with top N(Se ) ranks. The individual with better fitness and fewer component numbers will be assigned better rank. Let Pop denotes the group of all the individuals, individuali denotes the ith individual, and individual rank denotes the ith individual’s rank. i

Then the pseudocode of the elitist set selection algorithm is proposed in Figure 2.

for ( i = 1; i <  n ; i + + )

• individual _ rank = i ;

• end for ;

for ( i = 1; i <  n ; i + + )

if ( fitiness ( individual , ) >  fitness ( individual j )

• if ( individual _ rank >  individual j _ rank ) change _ rank ( individual_i , individual );

• end if ;

else if ( fitiness ( individual ) = fitness ( individual j ) if ( individual _ rank >  individual j _ rank and component _ num ( individual ) <  component _ num ( individual _j ))

• change _ rank ( individual_i , individual_j );

• end if ;

• end if ;

• end for ;

for ( i = 1; i <  n ; i + + )

if ( individual _ rank <  N )

S_e = S_e и individual, ;

• end if ;

• end for ;

• Figure 2. The pseudocode of the elitist set selection algorithm.

• C. The Proposed Algorithm HME-GA

The detailed process of HME_GA contains five steps: Initialization, crossover and mutation, elitist set selection, hyper-mutation and termination judgement. The process is described as follows.

• 1)    Initialization: The initialization process needs to randomly generate n initial individuals and evaluate the fitness values of each individual.

• 2)    Crossover and mutation: The crossover operation randomly chooses two parents from the last generation and generates two children. The number of times crossover implementing is confined by the crossover rate. The mutation operation randomly chooses one parent and generates one child. The number of times mutation implementing is confined by the mutation rate.

• 3)    Elitist set selection: After the crossover and mutation operations, the elitist set will be selected. The elitist set selection algorithm is shown in Figure 2.

• 4)    Hyper-mutation: The hyper-mutation operation randomly selects one parent from the elitist set and generates one child. The number of times hyper-mutation implementing is confined by the hyper-mutation rate.

• 5)    Termination judgment: If the algorithm fulfils the termination conditions, the process will stop. Else, the process will jump to step 2).

IV.    Experiments and results discussions

To demonstrate the performance improvement of HME-GA compared with traditional GA, We propose four experiments: Low-pass filter evolution, high-pass filter evolution, band-pass filter evolution and band-stop filter evolution. As these four experiments are essential problems in filter design, they can comprehensively demonstrate the proposed algorithm’s performance.

The parameters and experiments specifications are described as follows: The population size of GA is set to 100 and the generation-number is set to 300. The crossover rate and mutation rate of HME-GA and traditional GA are empirically set as 0.8 and 0.1. The size of the elitist group is set as 0.2 • n . This elitist group size is tested to be appropriate. The hyper-mutation rate increases from 0.1 to 1.0. The specifications of the four experiments are defined in TABLE II. All the experiments are repeated for 10 times with different random seeds in order to ensure the generalization of the results.

There are three subsections in this section: The first subsection proposes the low-pass filter evolving experiment. This experiment is used to demonstrate the advantages of HME-GA on analog circuit design. The second subsection proposes high-pass filter, band-pass filter and band-stop filter experiments in order to provide generalized proof for our argument. The third subsection summarizes the experiments and discussions in this section.

TABLE II.

The Specifications of The Low-pass Filter, High-pass Filter, Band-pass Filter and Band-stop Filter Experiments.

Experiment name	Specifications
Low-pass filter	Pass band: 1000Hz Stop band: 2000Hz Pass band gain: -3dB Stop band gain: -60dB
High-pass filter	Pass band: 2000Hz Stop band: 1000Hz Pass band gain: -3dB Stop band gain: -60dB
Band-pass filter	Pass band: 2000Hz, 3000Hz Stop band: 1000Hz, 4000Hz Pass band gain: -3dB Stop band gain: -60dB
Band-stop filter	Pass band: 1000Hz, 4000Hz Stop band: 2000Hz, 3000Hz Pass band gain: -3dB Stop band gain: -60dB

• A.    Low-pass Filter Evolving Experiment

TABLE III shows the average, best and worst fitnesses of HME-GA, GA with hyper-mutation and traditional GA on the low-pass filter’s evolving experiment. The best result is obtained by The HME-GA with hyper-mutation rate of 1.0. Considering the best results of the traditional GA, GA with hyper-mutation and HME-GA, HME-GA is outstanding in most conditions. There are only two conditions that HME-GA performs at a disadvantage than GA with hyper-mutation: The condition with hyper-mutation rates of 0.3 and 0.7. That means, HME-GA is more accomplished in finding excellent analog circuits than GA with hyper-mutation. It also reflects that, the elitist strategy works effectively in HME-GA. hyper-mutation strategy endows GA with better convergence than traditional GA on automated analog circuit design problems. On the whole, the performances of HME-GA and GA with hyper-mutation are all better than traditional GA.

TABLE III.

The average, best and worst fitness comparison among Traditional GA, HME-GA and GA with hyper-mutation on Low-pass Filter evolving Experiment.

Algorithm	Hypermutation rate	Fitness
		Avg.	Best	Worst
Traditional GA	N/A	14.244	12.207	15.806
HME-GA	0.1	7.659	4.328	13.805
	0.2	8.920	7.322	9.737
	0.3	10.786	7.317	17.569
	0.4	6.270	3.771	9.116
	0.5	9.351	4.288	17.572
	0.6	10.147	6.420	17.583
	0.7	8.873	2.783	13.446
	0.8	18.008	8.864	27.527
	0.9	13.599	5.484	27.527
	1.0	9.089	2.739	17.568
GA with hypermutation	0.1	8.694	6.372	11.284
	0.2	10.879	10.359	11.841
	0.3	10.880	5.966	15.856
	0.4	8.550	7.178	10.467
	0.5	7.670	6.096	8.883
	0.6	7.910	7.167	8.914
	0.7	8.581	6.703	9.553
	0.8	9.704	5.242	13.151
	0.9	7.890	5.041	12.501
	1.0	5.937	4.135	7.885

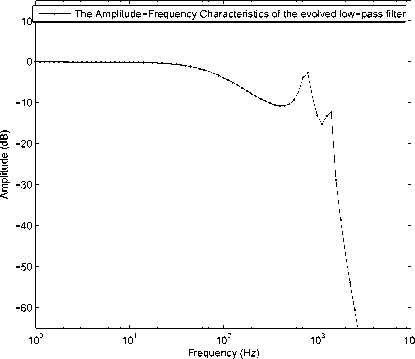
Figure 6. The amplitude-frequency characteristics result of the low-pass filter.

The average fitnesses of HME-GA and GA with hyper-mutation are approximately on the same level. But that doesn’t means the performances of HME-GA and GA with hyper-mutation are on the same level. It is mentioned above that, HME-GA is more accomplished in finding excellent analog circuits than GA with hypermutation. When we use HME-GA to design analog circuits, we always choose the best result. So, HME-GA is more useful than GA with hyper-mutation on practical applications. Figure 6 shows the amplitude-frequency characteristics result and Figure 12 shows the low-pass filter circuit that evolved by HME-GA.

• B.    High--pass Filter, Band-pass Filter and Band-stop Filter Evolving Experiments

TABLE IV, TABLE V and TABLE VI show the average, best and worst fitnesses of HME-GA, GA with hyper-mutation and traditional GA on the high-pass filter, band-pass filter and band-stop filter design experiments. Figure 8, Figure 9 and Figure 10 shows the shows the amplitude-frequency characteristics results of the high-pass filter, band-pass filter and band-stop filter. Figure 13, Figure 11 and Figure 7 shows the circuits of the high-pass filter, band-pass filter and band-stop filter.

TABLE IV.

The average, best and worst fitness comparison among Traditional GA, HME-GA and GA with hyper-mutation on High-pass Filter evolving Experiment.

Algorithm	Hypermutation rate	Fitness
		Avg.	Best	Worst
Traditional GA	N/A	12.581	10.398	16.584
HME-GA	0.1	8.235	5.982	19.875
	0.2	8.653	7.256	12.987
	0.3	9.587	6.871	11.487
	0.4	6.298	3.235	13.250
	0.5	7.532	4.581	13.257
	0.6	10.023	5.998	16.524
	0.7	6.358	3.669	15.983
	0.8	16.493	8.435	25.778
	0.9	13.265	5.984	25.684
	1.0	8.782	2.354	16.897
GA with hypermutation	0.1	7.986	8.542	11.852
	0.2	11.235	12.036	11.036
	0.3	9.487	5.573	16.058
	0.4	8.874	6.923	10.826
	0.5	6.998	7.005	8.450
	0.6	8.023	7.326	9.361
	0.7	8.254	6.302	10.842
	0.8	10.001	5.581	12.365
	0.9	8.025	4.960	13.684
	1.0	6.398	4.236	10.587

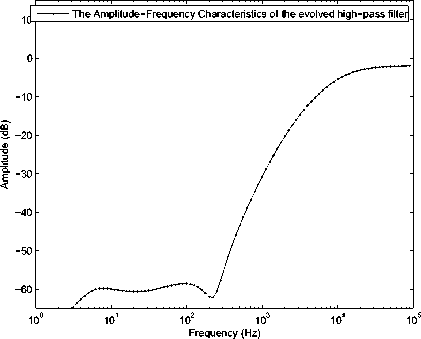
Figure 8. The amplitude-frequency characteristics result of the high-pass filter.

In the high-pass filter design experiment and the band-pass design experiment, the best fitnesses are obtained by HME-GA with hyper-mutation rate 1.0. In the band-stop design experiment, the best fitness also obtained by HME-GA, but the hyper-mutation rate is 0.8. Considering the ‘Best Fitness’ columns of all the four tables, it can be infered that: Though sometimes HME-GA with high hyper-mutation rate may performs at a disadvantage comparing with low hyper-mutation rate conditions, generally, HME-GA with high hypermutation rate is more likely to find better solutions.

TABLE V.

The average, best and worst fitness comparison among Traditional GA, HME-GA and GA with hyper-mutation on Band-pass Filter evolving Experiment.

Algorithm	Hypermutation rate	Fitness
		Avg.	Best	Worst
Traditional GA	N/A	13.731	12.207	15.806
HME-GA	0.1	8.652	6.964	13.805
	0.2	7.523	8.091	9.737
	0.3	9.671	7.925	17.569
	0.4	5.921	4.006	9.116
	0.5	8.169	3.991	17.572
	0.6	7.926	4.915	17.583
	0.7	8.791	5.698	13.446
	0.8	14.582	7.889	27.527
	0.9	16.220	4.985	27.527
	1.0	7.368	3.954	17.568
GA with hypermutation	0.1	12.694	7.925	15.964
	0.2	10.332	3.981	19.784
	0.3	8.752	6.891	15.856
	0.4	9.116	7.913	12.873
	0.5	7.249	5.913	9.985
	0.6	7.308	6.787	8.991
	0.7	9.479	7.618	12.549
	0.8	6.790	5.716	13.318
	0.9	7.106	4.937	16.549
	1.0	6.873	4.625	10.546

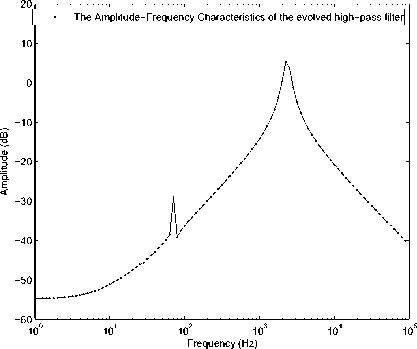
Figure 9. The amplitude-frequency characteristics result of the bandpass filter.

Considering the ‘Worst Fitness’ columns of all the four tables, HME-GA may performs not very well. But it is not considered a drawback for analog circuit design problems. When we use HME-GA to design analog circuits, the algorithm can generate many different circuits that fulfil the requirements, but we only use the best one.

TABLE VI.

The average, best and worst fitness comparison among Traditional GA, HME-GA and GA with hyper-mutation on Band-stop Filter evolving Experiment.

Algorithm	Hypermutation rate	Fitness
		Avg.	Best	Worst
Traditional GA	N/A	12.657	9.173	14.857
HME-GA	0.1	8.246	4.662	13.584
	0.2	7.654	6.492	8.995
	0.3	11.734	5.713	18.726
	0.4	7.951	2.997	22.384
	0.5	8.764	3.972	18.971
	0.6	11.730	7.964	16.547
	0.7	8.924	5.158	14.230
	0.8	7.981	2.159	28.981
	0.9	15.724	5.977	16.235
	1.0	7.264	3.432	15.367
GA with hypermutation	0.1	8.972	5.946	13.057
	0.2	9.825	6.348	11.665
	0.3	11.246	5.443	19.871
	0.4	7.463	6.337	8.468
	0.5	8.952	6.847	13.792
	0.6	6.741	4.762	9.574
	0.7	7.682	5.932	10.469
	0.8	8.612	7.876	9.826
	0.9	5.997	3.542	15.973
	1.0	6.753	4.678	11.527

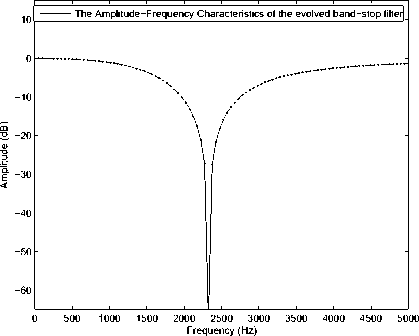
Figure 10. The amplitude-frequency characteristics result of the bandstop filter.

• C.    The Summary of The Four Experiments

The performances of HME-GA and GA with hypermutation are both better than traditional GA. That demonstrates the hyper-mutation’s importance in GA based analog circuit design. HME-GA is more efficient in finding high quality solutions than GA with hypermutation. That demonstrates elitist strategy makes the hyper-mutation mechanism more effective. HME-GA is demonstrated to be an efficient tool to automatically design analog circuits. HME-GA’s advantages also demonstrate that, topology design is as important as component values design. An appropriate trade-off between the intensity of topology evolving and the intensity of component values evolving should be chosen carefully.

V.    Conclusion

This paper proposed a hybrid algorithm HME-GA. HME-GA contains two essential strategies: The hypermutation strategy and the elitist strategy. Hyper-mutation is used to enhance GA’s ability on evolving analog circuit’s component values. Elitist is used to guide the hyper-mutation operation in order to make it working more efficiently. The experiments show that: HME-GA and GA with hyper-mutation are both better than GA. This consequence demonstrates that, hyper-mutation improves the GA’s performance on analog circuit design. HME-GA is more efficient in obtaining high-quality solutions than GA with hyper-mutation. This consequence demonstrates that, elitist strategy enhance the efficiency of hyper-mutation. The proposed algorithm is an efficient tool for analog circuit design.

Analog circuit design consists of circuit topology design and component values design. These two aspects are both essential to computer aided analog circuit evolving. It is discussed above; Traditional GA is not very efficient in evolving circuit component’s values. The advantage of HME-GA is that, it not only concentrates on evolving circuit topology, but also pays attention to evolving circuit component’s values.

Analog circuit has always been an important part of the electronic systems. So, analog circuit design automation is an important research area. Evolutionary technology is very useful in computer aided analog circuit design, and more potential of evolutionary methods on analog circuit design is waiting for exploring.

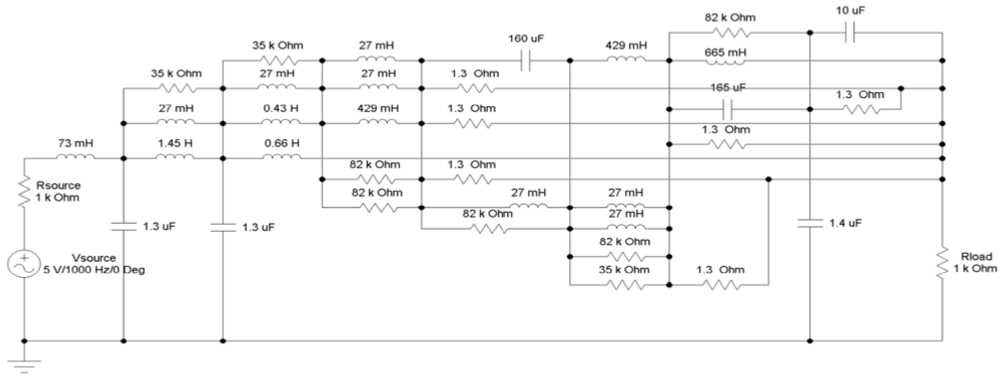
Figure 12. The circuit of the low-pass filter evolved by HME-GA.

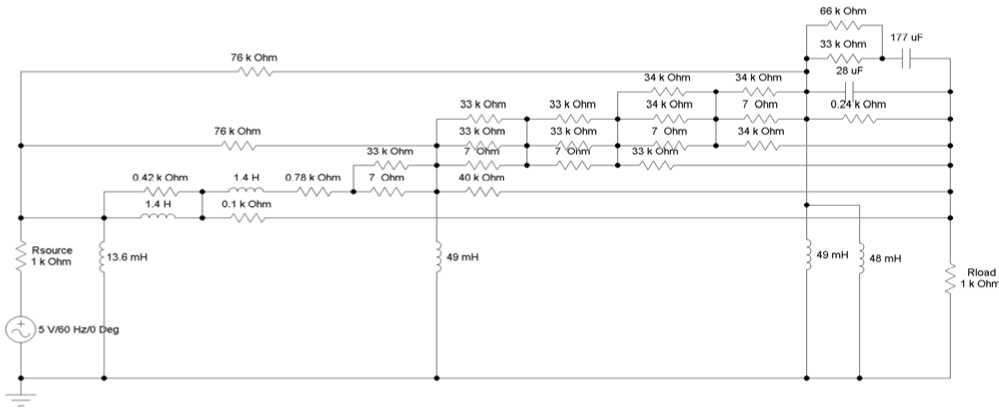
Figure 13. The circuit of the high-pass filter evolved by HME-GA.

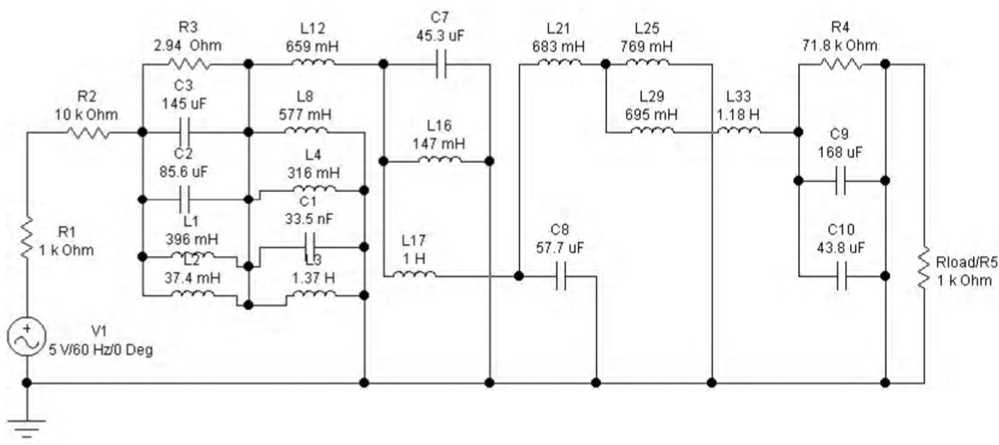
Figure 11. The circuit of the band-pass filter evolved by HME-GA.

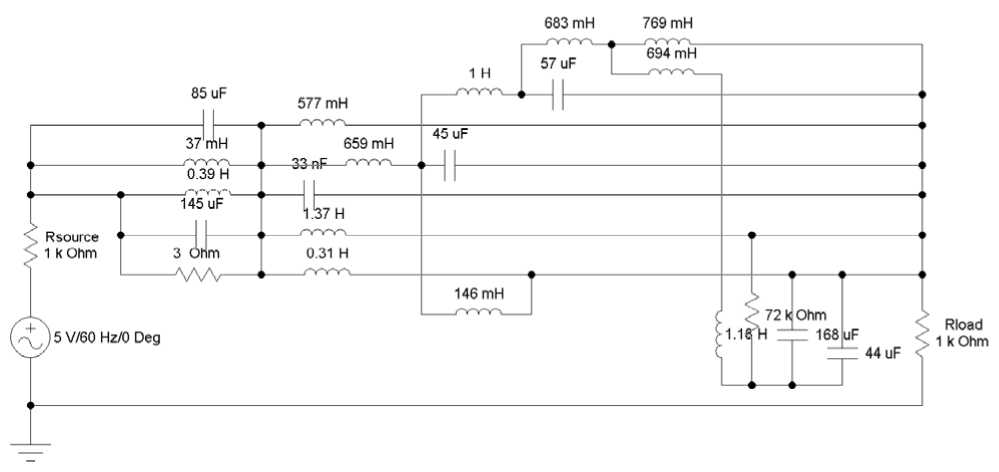
Figure 7. The circuit of the band-stop filter evolved by HME-GA.