Автокорреляционная модель высокотехнологичного экспорта регионов Российской Федерации

Автор: Красных Сергей Сергеевич

Журнал: Вестник Южно-Уральского государственного университета. Серия: Экономика и менеджмент @vestnik-susu-em

Статья в выпуске: 4 т.14, 2020 года.

Бесплатный доступ

В статье на базе данных Федеральной таможенной службы и Российского экспортного центра анализируется экспорт высокотехнологической продукции регионов Российской Федерации. С помощью методов пространственной эконометрики - глобального и локального индекса Морана - выделены территориальные кластеры концентрации высоких и низких значений высокотехнологичного экспорта, обнаружены полюса роста, которые могут выступать катализатором роста для соседних регионов.

Высокотехнологичный экспорт, регионы России, локальный индекс морана, глобальный индекс морана, пространственная автокорреляция

Короткий адрес: https://sciup.org/147232476

IDR: 147232476 | DOI: 10.14529/em200405

Текст научной статьи Автокорреляционная модель высокотехнологичного экспорта регионов Российской Федерации

Развитие высокотехнологического производства является одной из ключевых задач, стоящей на как на национальном, так и региональном уровне, поскольку экспорт высокотехнологичной продукции способен оказывать существенное положительное влияние на уровень и рост ВВП на душу населения [1]. В частности, развитие высокотехнологического экспорта закреплено в «майских» указах президента РФ и обозначено в национальном проекте «Международная кооперация и экспорт». В связи с чем целью данной работы является построение автокорреляционной модели высокотехнологического экспорта регионов России с помощью локального и глобального индекса Морана. Использование данного метода позволит выявить регионы с высокими значениями исследуемого показателя, а также обнаружить регионы, которые потенциально могут стать полюсами роста высокотехнологического производства.

Теория

В исследовании использован глобальный и локальный индексы Морана которые измеряет пространственную автокорреляцию, основанную одновременно на расположении объектов и их значениях. Согласно предложенному набору объектов и связанных с ними атрибутов, метод пространственной автокорреляции оценивает тип пространственных отношений между территориями -кластеризация, дисперсия или они расположены случайно. Этот метод рассчитывает глобальный индекс Морана, а также z-оценку и p-значение, чтобы оценить значимость индекса.

Индекс Морана является одним из самых старых инструментов пространственной автокорреляции. И рассчитывается как [2]:

ПН и

¹ = rS S ^{wtjZi Zj} / S ^z^ #⁽i)

° 1 = 1 7 = 1 i = l где zi - отклонение атрибута для i-го объекта от его среднего значения (xi — X); wt - - пространственный вес между объектами i, j, n, - общее количество объектов, - совокупность всех простран- ственных весов:

So =ZLW ij#(2) 1 = 1 7=1

Локальный индекс Морана рассчитывается как:

Xi — X V^ⁿ

It = У wij (Xj_X)# (3)

^(X j — X)²n — 1

X2# (4)

Значения этого индекса обычно находятся в диапазоне от –1,0 до +1,0, где отрицательное зна- чение индекса указывает на отрицательную пространственную автокорреляцию, а положительное значение, соответственно, на положительную пространственную автокорреляцию [3].

Z -оценка индекса Морана рассчитывается как: ₇ J — ^Е ( ) i I (W)

где E ( I) - ожидаемое значение I , а V (I) - дисперсия I , как показано в уравнении:

V (!) = Е(12 ) — Е 2(/)#(6)

Посредством создания весов создаются пространственные смежности. При этом определение соседства основывается на наличии общей границы [4]. Весы между пространственными объектами формируют матрицу пространственных весов, которая отражает интенсивность географических отношений между соседними объектами, то есть расстояние между соседями, протяженность общей границы [5]. На основе чего можно построить пространственную диаграмму рассеивания Морана [6]. Диаграмма рассеивания Морана представлена на рис. 1.

Квадрант LH: Автокорреляция данных территорий отрицательная, они имеют низкое значение анализируемого атрибута, окружены территориями с высокими значениями. Данные территории является зоной влияния территорий, входящих в квадрант НН и HL.

Квадрант НН:

Автокорреляция данных территорий положительная, они имеют высокое значение анализируемого атрибута, окружены территориями с высокими значениями. Данные территории не могут стать полюсами роста, т.к. обладают высокими значениями исследуемого показателя. Образуют кластер высоких значений.

Квадрант LL: Автокорреляция данных территорий положительная, они имеют низкое значение анализируемого атрибута, окружены территориями с такими же низкими значениями. Данные территории не испытывают влияния других территорий. Образуют кластер низких значений.

Квадрант HL:

Автокорреляция данных территорий отрицательная, они имеют высокое значение анализируемого атрибута, окружены территориями с низкими значениями. Данные территории не испытывают влияния других территорий. Данные территории являются полюсами ростами.

Рис. 1. Диаграмма рассеивания Морана

Результаты

В качестве исходных данных для построения модели брались объемы экспорта верхнего предела несырьевого неэнергетического экспорта, что по общей классификации характеризует данную категорию как экспорт высокотехнологической продукции (табл. 1).

В ходе построения модели, используя гло- бальный индекс Морана, можно заключить следующее: полученная z-оценка говорит о том, что существует тесная взаимосвязь между регионами, и показывает, что распределение между регионами является кластеризированным, а p-значение подтверждает статистическую значимость модели. Результаты пространственной автокорреляции представлены в табл. 2.

Таблица 1

Объем экспорта высокотехнологичной продукции регионов России за 2019 год

№	Регион	Объем экспорта (млн $)	№	Регион	Объем экспорта (млн $)
1	Москва	15 049,74	43	Республика Бурятия	143,13
2	Московская область	6 009,77	44	Архангельская область	137,42
3	Санкт-Петербург	3 467,70	45	Ставропольский край	137,37
4	Свердловская область	3 103,18	46	Кировская область	127,47
5	Нижегородская область	2 047,33	47	Курская область	126,46
6	Новосибирская область	1 314,85	48	Новгородская область	121,32
7	Ростовская область	1 115,50	49	Вологодская область	119,65
8	Тульская область	1 106,83	50	Орловская область	117,93
9	Ульяновская область	1 085,09	51	Тюменская область	89,86
10	Республика Татарстан	1 033,57	52	Ивановская область	86,86
11	Приморский край	1 012,68	53	Оренбургская область	74,73
12	Ленинградская область	996,19	54	Костромская область	73,83
13	Республика Башкортостан	984,04	55	Республика Марий Эл	73,49
14	Рязанская область	973,79	56	Псковская область	58,18
15	Самарская область	948,43	57	Томская область	52,93
16	Челябинская область	693,43	58	Тамбовская область	47,53
17	Красноярский край	607,89	59	Республика Карелия	45,5

Окончание табл. 1

№	Регион	Объем экспорта (млн $)	№	Регион	Объем экспорта (млн $)
18	Ярославская область	557,77	60	Ханты-Мансийский автономный округ – Югра	37,63
19	Удмуртская Республика	539,92	61	Хабаровский край	34,34
20	Краснодарский край	479,48	62	Мурманская область	33,04
21	Омская область	478,28	63	Республика Коми	22,21
22	Калужская область	476,43	64	Республика Крым	17,17
23	Пермский край	456,39	65	Республика Северная Осетия – Алания	15,19
24	Владимирская область	428,9	66	Республика Дагестан	15,18
25	Белгородская область	428,46	67	Республика Алтай	15,04
26	Алтайский край	366,39	68	Кабардино-Балкарская Республика	11,89
27	Кемеровская область	361,21	69	Ямало-Ненецкий автономный округ	9,65
28	Смоленская область	339,16	70	Республика Адыгея	9,51
29	Иркутская область	301,82	71	Забайкальский край	6,65
30	Саратовская область	288,65	72	Севастополь	5,51
31	Липецкая область	218,3	73	Амурская область	4,91
32	Курганская область	211,52	74	Камчатский край	4,19
33	Пензенская область	210,08	75	Карачаево-Черкесская Республика	2,79
34	Волгоградская область	190,32	76	Республика Калмыкия	2,57
35	Тверская область	187,05	77	Республика Хакасия	2,42
36	Астраханская область	181,44	78	Республика Саха (Якутия)	2,26
37	Воронежская область	179,16	79	Магаданская область	1,01
38	Сахалинская область	176,76	80	Республика Ингушетия	0,68
39	Брянская область	168,5	81	Еврейская автономная область	0,41
40	Калининградская область	167,59	82	Чеченская Республика	0,36
41	Чувашская Республика	154,46	83	Чукотский автономный округ	0,25
42	Республика Мордовия	152,12

Примечания: Рассчитано автором по официальным данным Федеральной службы государственной статистики:

Таблица 2

Отчет о пространственной автокорреляции субъектов РФ по показателю объема экспорта высокотехнологической продукции

Показатель	Значение
Индекс Морана	0,242673
z-оценка	4,605074
p-значение	0,000004
Дисперсия	0,003060

Далее в ходе исследования был проведен анализ кластеров и выбросов на основе локального индекса Морана. Данный метод позволяет определить кластеры высоких значений, кластеры низких значений, и на основе этого определить тип взаи- моотношений между территориями. Графическое отображение результатов данного анализа представлено на рис. 2.

На основе данного анализа можно заключить, что г. Москва, г. Санкт-Петербург, Калужская, Ленинградская, Московская, Нижегородская, Самарская, Тульская, Челябинская области, Республика Татарстан образуют кластер высоких значений (территории HH), данные территории имеют высокое значение исследуемого показателя и могут оказывать положительное влияние на территории LH, находящиеся по соседству.

Архангельская, Белгородская, Брянская, Владимирская, Волгоградская, Вологодская, Воронежская, Ивановская, Калининградская и другие

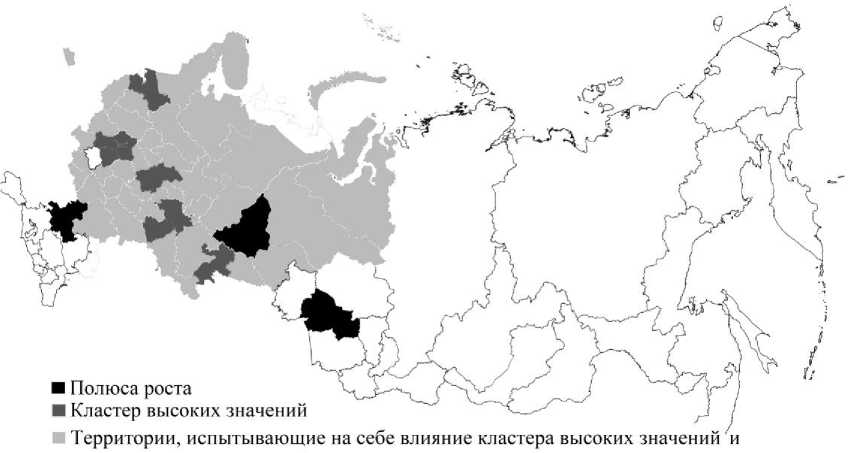
полюса роста

□ Кластер низких значений, переферия

Рис. 2. Графическое отображение результатов анализа методом локального индекса Морана

регионы, выделенные серым цветом, относятся к территориям LH, они имеют низкое значение исследуемого показателя, но находятся по соседству с регионами, имеющими высокий уровень объема экспорта технологической продукции, их можно охарактеризовать как территории периферии, которые испытывают на себе влияние кластера высоких значений.

Новосибирская, Ростовская и Свердловская области относятся к территориям HL, они имеют высокое значение уровня объема экспорта высокотехнологической продукции, окружены территориями с низким уровнем исследуемого показателя, данные территории являются полюсами роста.

Республика Дагестан, Карачаево-Черкесская Республика, Ставропольский край, Чеченская Республика, Республика Ингушетия, Республика Северная Осетия-Алания, Кабардино-Балкарская Республика, Краснодарский край, Республика Саха (Якутия), Красноярский край и другие регионы, выделенные белым цветом, образуют кластер низких значений (территории LL), что характеризует их как территории, не испытывающие на себе влияния других регионов.

Обсуждение и выводы

Таким образом, можно заключить, что Новосибирская, Ростовская и Свердловская области могут стать полюсами роста экспорта высокотехнологической продукции, а за счет территориального соседства с территориями LH (темный цвет), могут выступать катализатором роста для соседних регионов, но для этого необходимы инвести- ции для создания условий и построения необходимой производственной инфраструктуры.

Статья подготовлена в соответствии с Планом НИР для лаборатории моделирования пространственного развития территорий ФГБУН Института экономики УрО РАН на 2021 год.

Список литературы Автокорреляционная модель высокотехнологичного экспорта регионов Российской Федерации

Peneder, M. Industrial structure and aggregate growth, Structural Change and Economic Dynamics. 2002. V. 14. P. 427-48.
Anselin, L. Local Indicators of Spatial Association - LISA. Geographic Analysis. 1995. V. 27. P. 93-115. DOI: 10.1111/j.1538-4632.1995.tb00338.x
Songchitruksa P., Zeng X. Getis-Ord Spatial Statistics to Identify Hot Spots by Using Incident Management Data. Transportation Research Record: Journal of the Transportation Research Board. 2010. Vol. 2165. P. 42-51. DOI: 10.3141/2165-05
Красных С.С. Автокорреляционный анализ межрегиональных взаимосвязей в процессах добычи полезных ископаемых в Уральском федеральном округе // Материалы VII Информационной школы молодого ученого. 2019. С. 285-291.
Павлов Ю.В., Королева Е.Н. Пространственные взаимодействия: оценка на основе глобального и локального индексов Морана // Пространственная экономика. 2014. № 3. С. 95-110.
Anselin L. The Moran Scatterplot as an ESDA Tool to Assess Local Instability in Spatial Association // In Spatial Analytical Perspectives on Gis in Environmental and Socio-Economic Sciences. 1996. P. 111-125.

Статья научная

Автокорреляционная модель высокотехнологичного экспорта регионов Российской Федерации

Текст научной статьи Автокорреляционная модель высокотехнологичного экспорта регионов Российской Федерации

1 = rS S wtjZi Zj / S z^ #(i)

Список литературы Автокорреляционная модель высокотехнологичного экспорта регионов Российской Федерации

¹ = rS S ^{wtjZi Zj} / S ^z^ #⁽i)