Автолик Питанский. О восходах и заходах

гократно ссылается на одну из теорем из «О движущейся сфере».1 Впрочем, есть в тексте «О движущейся сфере» и теоремы, которые в сочинении «О восходах и заходах» никак не используются, насколько мы можем судить о ходе мысли автора.

«О движущейся сфере» былo включенo Паппом Александрийским в его «Малую Астрономию». Вообще, тексты Автолика – одни из самых ранних из дошедших до нас математических сочинений, в этом с ними соперничают лишь «Феномены» Эвклида. Если бы один из этих математиков явно сослался на другого, это могло бы внести ясность в хронологию. Но поскольку они этого не делают, то существуют различные мнения о том, предшествовал ли «О движущейся сфере» Автолика «Феноменам» Эвклида (Heath 1921: 349) или нет (Neugebauer 1975: 4). Как бы то ни было, Автолик – очень важная фигура в истории греческой науки.

Замечания о тексте

Трактат «О восходах и заходах» дошел до нас состоящим из двух книг: первая содержит 13 теорем, а вторая – 18. Текст установлен двумя издателями: Фридрихом Хульчем (Hultsch 1885) и Жозефом Моженэ (Mogenet 1950). Наш перевод основывается в целом на тексте Моженэ, хотя в некоторых оговоренных случаях мы учли точку зрения Хульча.

Трактат сохранился не целиком. Об этом свидетельствуют древние схолии к нему: в одном месте во второй книге схолиаст ссылается на теорему 10 из первой книги (см. прим. 164) , но теорема под этим номером говорит совсем не о том, зато предшествующая ей (девятая) теорема дает аналогичное нужному утверждение, так что несомненно, что за ней раньше следовала аналогичная теорема, на которую и ссылается схолиаст (и формулировку которой поэтому можно достаточно уверенно восстановить: см. прим. 71) . Немного дальше, в схолиях мы наталкиваемся на отсылку к теореме 19 (чтение Моженэ) или 15 (чтение Хульча) из первой книги, которая, как было сказано, в настоящее время содержит всего 13 теорем. Таким образом, несомненно, что некоторые теоремы из этой книги так или иначе выпали.

Для второй книги явных свидетельств неполноты нет, хотя отдельные странности заставляют задуматься об этом. Вместе с тем, она существенно отличается от первой книги по стилю изложения. Никак не претендуя на серьезный текстологический анализ, выскажем предположение: нам кажется, что она была создана существенно позднее первой книги, когда методологические установки Автолика успели заметно измениться. Автолик в ней вольнее обходится с терминологией. Например, в первой книге вводятся термины «видимый утренний восход» (φαινομένη ἑῴα ἀνατολή) и ему подобные, и Автолик их твердо придерживается (иногда только меняется порядок прилагательных, что может быть и вольностью переписчика). Во второй книге наряду с этими терминами без объяснения вводятся выражения типа «восходит утром» (ἑῷον ἀνατέλλει), которые, как можно судить по их употреблению в доказательствах, имеют то же значение, но не содержат эквивалента слова «видимый». Этот терминологический разнобой – уже несомненное изменение стиля изложения, но все же это мелочь. Гораздо существеннее то, что в первой книге Автолик стремится аккуратно доказывать каждую деталь, что иногда приводит к довольно длинным доказательствам, состоящим из похожих пассажей, а во второй книге многое остается недосказанным, доказательства сжаты и часто обрублены по принципу «а остальное аналогично». Причем нельзя сказать, что материал во второй книге заметно сложнее. Скорее складывается ощущение, что изменился modus operandi автора, как будто Автолик перестал считать нужным описывать каждый шаг.

Замечания о математической и астрономической терминологии

Хорошо известно, что научные термины древних авторов представляют особую проблему для перевода. Прежде всего, существует то общее обстоятельство, что перед нами терминология из математической традиции, отличной от нашей. То, что наша математическая традиция выросла именно из древнегреческой, представляет специфическую трудность. Многие термины в современном математическом узусе являются прямыми потомками греческих, но их значение не всегда в точности совпадает с древним. Более того, то, что в наше время является четким и неизменным термином, для раннего греческого автора, такого как Автолик, еще могло быть просто выражением, которое он варьировал от случая к случаю. В качестве примера возьмем термин «горизонт». В современном научном тексте он не может заменяться на, скажем, «горизонтальный круг» или что-либо еще в этом роде: термин зафиксирован. Но слово «горизонт» восходит к древнегреческому ὁρίζων, что означает «разделяющий». По-видимому, первоначально его употребление в обороте типа «круг, разделяющий видимую и невидимую части небесной сферы». Со временем стал допустимым просто «разделяющий круг» (ὁρίζων κύκλος), поскольку считалось, что читателю уже известно, что именно он разделяет. Третьим шагом стало отбрасывание слова «круг»: посредством столь свойственной древнегреческому языку субстантивации прилагательное превращается существительное (ὁ ὁρίζων), которое и дает современное «горизонт». В переводимом тексте Автолика засвидетельствованы все три варианта, но последний встречается чаще всего. Фактически, мы наблюдаем у Автолика рождение термина «горизонт». То же можно сказать о термине «зодиак». Для некоторых терминов дело дополнительно осложняется тем, что они уже в античности были переведены на латинский язык и перешли в современные языки оттуда. Таков, например, термин «меридиан» (лат. meridianus): он является латинским переводом греческого слова μεσημβρινός («полуденный»), которое, аналогично горизонту, является субстантивированным прилагательным, а следовательно, еще раньше это был «полуденный круг» (у Автолика такая форма не встречается, но она засвидетельствована в «Феноменах» Эвклида). Все это ставит переводчика перед необходимостью решать: переводить ли ὁρίζων κύκλος всегда буквально, как «разделяющий круг», или как «горизонт», или еще как-то, или же поступать в разных случаях по-разному. Сразу скажем, что мы не ставили перед собой задачи перевести Автолика так, чтобы все термины в переводе были в согласии с современным узусом: нам кажется допустимым и даже иногда желательным использовать выражения, которые необычны для современной математики, зато дают почувствовать своеобразие математики древней (разумеется, все это не должно быть в ущерб ясности изложения).

В некоторых случаях древняя терминология в переводе выглядит ошибочной с современной точки зрения. Например, в современном понимании круг – это область на плоскости, а окружность – линия, граница круга. Греческий термин κύκλος может значить и «круг», и «окружность». Мы предпочли первый вариант (включая и перевод ἡμικύκλιον словом «полукруг», а не «полуокружность»), хотя везде в данном сочинении (но не везде в «О движущейся сфере») современная терминология требовала бы «окружность». Дополнительным аргументом в пользу такого решения служит то, что и в современной русской математической терминологии имеется важное для астрономии исключение из дихотомии круг-окружность. А именно: окружность наибольшего возможного радиуса на сфере и сейчас именуется «большой круг». Более того, в этом выражении и прилагательное «большой» – старинная узаконенная ошибка перевода: термин восходит к греческому μέγιστος κύκλος (Автолик его использует), так что и с языковой, и с математической точек зрения правильно было бы «наибольшая окружность». Мы, однако, смирились с этим и переводим μέγιστος κύκλος традиционным русским термином «большой круг».

Таким образом, математическая терминология в переводе иногда выглядит некорректно с современной точки зрения, но это сделано сознательно, с целью ближе передать язык Автолика (с учетом обоих его сочинений, а не только «О восходах и заходах») и своеобразие древней математики вообще. Ниже в таблице мы приводим список терминов, встречаемых в переводимом тексте, которые, по нашему мнению, могли бы породить вопросы.

В подлиннике	Перевод	Значение
κύκλος	круг	Обычно окружность, но может быть и круг (они не различаются терминологически). В «О восходах и заходах» – всегда окружность.
ἡμικύκλιον	полукруг	Полуокружность.
μέγιστος κύκλος	большой круг	Большой круг.
περιφέρεια	дуга	Дуга.
ὁρίζων κύκλος, ὁρίζων	горизонт	Горизонт.
παράλληλος κύκλος, παράλληλος	параллельный круг	Любая окружность на небесной сфере, соосная оси суточного вращения. Отсюда современный термин «параллель».
μεσημβρινός	меридиан	Любой большой круг, проходящий через полюса небесной сферы.
τοῦ ἡλίου κύκλος	круг солнца	Эклиптика.
ζῳδίων κύκλος	круг зодиака	Эклиптика.
ζῳδιακός κύκλος	зодиакальный круг	Эклиптика.
ζῳδιακός	зодиак	Эклиптика.
ζῴδιον	знак зодиака	Букв. «фигурка». Это мера дуги эклиптики, равная 30°, поскольку эти знаки делят эклиптику на 12 равных частей. К дугам не на эклиптике не применяется.
ἰσημερινός	круг равноденствия	Небесный экватор.
τροπικός	тропик	Окружность на небесной сфере, соосная оси суточного вращения и касающаяся эклиптики.
φάσις	появление	Всякое видимое нахождение звезды над горизонтом.
ἀληθινή ἑῴα ἀνατολή	истинный утренний восход	Утренний космический восход.

ἀληθινή ἑῴα δύσις	истинный утренний заход	Утренний космический заход.
ἀληθινή ἑσπερία ἀνατολή	истинный вечерний восход	Вечерний космический восход.
ἀληθινή ἑσπερία δύσις	истинный вечерний заход	Вечерний космический заход.
φαινομένη ἑῴα ἀνατολή	видимый утренний восход	Гелиакический восход.
φαινομένη ἑῴα δύσις	видимый утренний заход	Гелиакический заход.
φαινομένη ἑσπερία ἀνατολή	видимый вечерний восход	Акронический восход.
φαινομένη ἑσπερία δύσις	видимый вечерний заход	Акронический заход.
περιφορά	обращение	Полный оборот светила в суточном вращении (или время, которое он занимает, т.е. сутки).
συζυγία	сопряжение	Сизигия, расположение каких-либо небесных тел в диаметрально противоположных точках неба.

Замечания о модели Автолика

Автолик рассматривает небесную сферу с наблюдателем в центре. На поверхности сферы находятся звезды и начерчен большой круг (эклиптика, или, как ее обычно называет Автолик, зодиак), по которому движется солнце, совершая один оборот за один год. Планеты и луну Автолик не рассматривает (он четко оговаривает это: «неподвижные звезды»). Далее, вся сфера, вместе со звездами и эклиптикой, вращается в суточном движении неба. Горизонт является большим кругом2 сферы, который, в отличие от эклиптики, не участвует в суточном вращении: суточное вращение сферы происходит относительно горизонта. Угол между эклиптикой и осью суточного вращения – это то, что с современной точки зрения является углом между земной осью и плоскостью земной орбиты вокруг солнца, то есть около 23° в настоящее время, но ближе к 24° во времена Автолика (этот угол по ряду причин меняется со временем сложным образом, но лишь ненамного и медленно). Угол же между горизонтом и осью суточного вращения опреде- ляется географической широтой наблюдателя. Автолика нигде не интересуют численные значения этих углов, но он всегда предполагает, что наблюдатель находится в северном полушарии, так что видимый ему полюс небесной сферы – северный. В связи с этим следует помнить, что во всех теоремах, где используются понятия юга и севера, они должны поменяться местами в случае наблюдателя в южном полушарии. Автолик не мог не знать этого, однако решил ограничиться практическим случаем северного полушария: даже греческое стремление к абстрактности имело пределы.

Солнце в модели движется по эклиптике с постоянной скоростью, причем Автолик обозначает «знаком зодиака», «месяцем» и «тридцатью днями» одну двенадцатую часть полной окружности, то есть года (один знак зодиака эквивалентен месяцу). Это не неточность, а условность терминологии, которую можно назвать округлением: Автолик, разумеется, знал, что год составляет не 360 дней. В теореме 1.6 он явно указывает, что год состоит из целого числа дней и еще четверти (т.е. 365,25), и можно предполагать, что он знал, что и это не абсолютно точно. Также, Автолик пренебрегает скоростью движения Солнца по эклиптике в сравнении со скоростью его суточного вращения: он рассматривает утренние и вечерние явления при положении солнца в одной и той же точке эклиптики и может по этому поводу сказать «они происходят в одну ночь». Математически, когда Автолик ведет доказательство, он имплицитно пренебрегает тем, что солнце успевает немного сдвинуться по эклиптике даже в течение одной ночи. Иными словами, в масштабе года «одна ночь» для Автолика является одним моментом времени. Разумеется, если взглянуть на его теоремы не как на абстрактные математические утверждения, а как на утверждения о реальных астрономических наблюдениях, то такой уровень точности совершенно достаточен.

Для наблюдателя на некоторой географической широте 6 заходят и восходят только звезды со склонением в пределах ±(90° - |5|). Например, для наблюдателя в северном полушарии (5 > 0) звезды, лежащие слишком близко к северному небесному полюсу, всегда остаются над горизонтом, а лежащие слишком близко к южному небесному полюсу всегда остаются под горизонтом, то есть вообще не наблюдаются. Поэтому, строго говоря, все утверждения Автолика о восходах и заходах звезд нуждаются в оговорке, что это для тех звезд, у которых восходы и заходы вообще бывают. Естественно, Автолик отдавал себе в этом отчет³, но он практически никогда этого не оговаривает.

Большое значение для Автолика (и вообще для древней астрономии) играют гелиакические и акронические восходы и заходы звезд, и название «О восходах и заходах» в первую очередь имеет в виду именно их. Гелиакические явления называются в переводе утренними (ἑῷος), а акронические вечерними (ἑσπέριος). Их определения даны в самом начале трактата. Здесь мы хотим только пояснить их сущность. Наивно можно было бы ожидать, что темное время суток имеет место всегда, когда солнце находится под горизонтом, и тогда любая находящаяся над горизонтом звезда видима. В реальности, если солнце находится ниже горизонта, но достаточно близко к нему, некоторое количество солнечного света (утренняя или вечерняя заря) заполняет небо и затмевает звезды. Гелиакические и акронические восходы и заходы звезды (их иногда называют восходами и заходами в лучах утренней или вечерней зари) – это предельные случаи, когда звезда пересекает горизонт при солнце, находящемся под горизонтом на том минимальном расстоянии, при котором звезда видима. Для конкретной звезды эти явления происходят, следовательно, только в определенные дни года, что и делало их основой для календарей: древние цивилизации использовали их как маркеры времени.4 Автолик считает данным, что эти явления происходят, когда солнце находится под горизонтом на глубине в 15° дуги эклиптики. Легко видеть, что в терминах Автолика это «половина знака зодиака».5 Этот факт играет фундаментальную роль и используется многократно. При этом угловой размер солнца (около 0,5°) Автолика не интересует: для его целей солнце – точка, как и любая звезда.

По нашему мнению, модель Автолика (как и эквивалентную ей модель «Феноменов» Эвклида) не следует рассматривать как его представление об устройстве мира. Солнце и звезды в модели расположены на одной сфере, так что Солнце может совпадать с той или иной звездой. Ясно, что Автолик никак не мог считать это реально происходящим событием (ни его, ни Эвклида явно не волновал вопрос, что происходит, когда Солнце физически сталкивается со звездой). Следовательно, он просто рассматривает проекции Солнца и звезд на некоторую сферу с точки зрения наблюдателя в центре сферы. Эта модель – чистая математическая абстракция. В частности, не рассматриваются никакие реальные звезды (скажем, Сириус): «звезда» – это просто синоним слова «точка», и не имеет значения, существует ли в рассматриваемой точке на небесной сфере реальная светящаяся звезда. Иными словами, модель Автолика-Эвклида – не описание их представлений об устройстве космоса, а математическая абстракция наблюдаемого неба.

Поэтому, в частности, нельзя даже быть полностью уверенным, что Автолик или Эвклид не были приверженцами гелиоцентрической модели. Они вполне могли считать, что Земля вращается вокруг Солнца, но не упоминали об этом, ибо это просто не имело отношения к математической модели наблюдаемого неба, с которой они имели дело.6 Это полностью аналогично современной наблюдательной астрономии: в ней по-прежнему используется понятие небесной сферы, рассматривается ее суточное вращение и движение Солнца по эклиптике относительно звезд, существуют двумерные карты неба. Но было бы нелепо делать из этого вывод, что современные авторы таких карт и книг отрицают гелиоцентрическую модель Солнечной системы, не знают, что Солнце, планеты и различные звезды на самом деле находятся на чрезвычайно различных расстояниях от нас, и что никакой «поверхности неба» на самом деле нет, и т. д.

Замечания о диаграммах

Сопровождающие теоремы диаграммы могут быть трудны для понимания, поэтому имеет смысл их оговорить заранее. Диаграммы в нашем переводе в общем воспроизводят диаграммы из рукописей, в том виде, в котором они воспроизведены в издании Моженэ. Они выполнены в стиле, очень сильно отличающемся от привычных нам геометрических чертежей. Мы сделали их трехмерность более явной, постарались придать всем элементам положения, более близкие к реальным,7 и добавили стрелки, обозначающие суточное вращение неба и движение солнца по эклиптике. Рассмотрим в ка- честве примера диаграмму на Рис. 1. Ее следует воспринимать как сферу, половина которой выступает из плоскости страницы. Это небесная сфера. Показанная сплошной линией окружность представляет собой горизонт. Северная сторона горизонта – вверху, восточная – справа. Направление суточного вращения неба показано круговой стрелкой в верху диаграммы. Ось этого суточного вращения лежит в вертикальной плоскости, перпендикулярной плоскости страницы. Ее направление зависит от географического положения наблюдателя: в северном полушарии (подразумеваемый Автоликом случай), эта ось направлена вверх и выходит из плоскости страницы под углом, равным географической широте наблюдателя. В предельном случае наблюдателя на экваторе Земли эта ось лежала бы в плоскости страницы, а для наблюдателя на северном полюсе она была бы перпендикулярна странице. Окружность AErZ, являющаяся большим кругом сферы и расположенная под углом, есть эклиптика. Солнце проходит эту окружность за год, двигаясь по ней со скоростью примерно 1° в день в направлении, указанном прямой стрелкой. Пунктирной линией показана часть эклиптики, в данный момент суточного вращения находящаяся под землей (за плоскостью страницы). При суточном вращении изображенная окружность AErZ вращается как целое: можно вообразить себе, что она начерчена на прозрачной сфере, которая и совершает суточное вращение. Угол между осью суточного вращения диаграммы и осью, перпендикулярной плоскости AErZ, есть, в современных терминах, угол наклона земной оси по отношению к оси земной орбиты. Точные значения всевозможных углов на диа-граммax не соблюдены, те или иные величины в них могут быть утрированы для удобства, но никогда не нарушая логики доказательства (например, если важно, что одна точка лежит правее другой, то этот порядок всегда будет соблюден). Таким образом, диаграммы представляют собой качественно, но не количественно верную картину происходящего.

Автолик Питанский

О ВОСХОДАХ И ЗАХОДАХ

Книга первая

Одни из восходов и заходов неподвижных8 звезд называются истинными, а другие видимыми.

Среди истинных есть: утренний восход, когда звезда восходит одновременно с восходящим солнцем; утренний заход, когда звезда заходит одновременно с восходящим солнцем; вечерний восход, когда звезда восходит одновременно с заходящим солнцем; вечерний заход, когда звезда заходит одновременно с заходящим солнцем.

Среди видимых9 есть: утренний восход, когда звезда впервые видна на восходе до восхода солнца;10 утренний заход, когда звезда впервые видна на заходе до восхода солнца; вечерний восход, когда звезда в последний раз видна на восходе после захода солнца;11 вечерний заход, когда звезда в последний раз видна на заходе после захода солнца.12

Теорема 1.1

У всякой13 неподвижной звезды видимые утренние восходы и заходы происходят позже истинных, а видимые вечерние восходы и заходы происходят раньше истинных.

Пусть круг ΑΒΓΔ является горизонтом космоса, а круг солнца14 располагается как ΑΕΓΖ, и пусть его восточная часть – та, что обращена к точке Δ, а западная – та, что обращена к точке Β (Рис. 1).15 Пусть полукруг ΑΕΓ находится под землей, и пусть некоторая неподвижная звезда восходит в точке Δ, в то время как солнце восходит в точке Α. То есть это истинный утренний восход звезды Δ. Я утверждаю, что видимый восход звезды Δ происходит позже истинного.

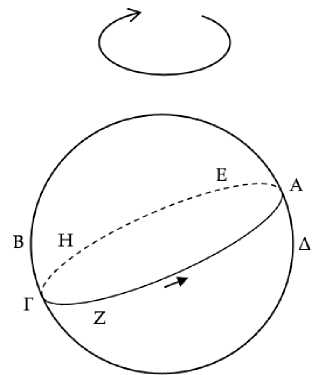
Рис. 1

Действительно, когда солнце восходит в точке Α, звезда Δ не видна на восходе16. Не видна она на восходе и когда солнце проходит дугу ΓΖΑ, как будет показано позже.17 Таким образом, звезда Δ покажется на восходе через несколько дней,18 когда солнце пройдет дугу такой продолжительности, что звезда Δ сможет избегать солнечных лучей. Итак, пусть она впервые станет видима при солнце в точке Е. Следовательно, при солнце в точке Е происходит видимый утренний восход звезды Δ. Поскольку солнце оказывается в точке А раньше, чем в точке Е, и в то время, когда оно в А, происходит истинный утренний восход звезды Д, а в то время, когда оно в Е, происходит видимый утренний восход, то получается, что видимый происходит позже истинного.

Опять-таки, пусть некоторая неподвижная звезда заходит в точке Β, в то время как солнце восходит в точке Α. То есть это истинный утренний заход звезды Β. Итак, я утверждаю, что видимый заход происходит позже истинного.

Действительно, когда солнце восходит в точке Α, звезда Β не видна на заходе. Не видна она на заходе и когда солнце проходит дугу rZA. Таким образом, звезда Β покажется на заходе через несколько дней19, когда солнце пройдет дугу такой продолжительности, что Β сможет избегать солнечных лучей. Итак, пусть звезда Β впервые избежит солнечных лучей при солнце в точке Е. То есть при солнце в точке Е происходит видимый утренний заход звезды В. Поскольку солнце оказывается в точке А раньше, чем в точке Е, и в то время, когда оно в Α, происходит истинный утренний заход звезды Β, а в то время, когда оно в Е, происходит видимый, то получается, что видимый происходит позже истинного.

Опять-таки, пусть некоторая неподвижная звезда восходит в точке А, в то время как солнце заходит в точке Γ. То есть это истинный вечерний восход звезды А. Я утверждаю, что видимый восход звезды А происходит раньше истинного.

Действительно, когда солнце заходит в точке Γ, звезда Δ не видна на восходе. Не видна она на восходе и когда солнце переходит в полукруг ΓΖΑ. Таким образом, звезда Δ будет видима на восходе до того, как солнце окажется в точке Γ. Итак, пусть она будет видима в последний раз при солнце в точке Η. То есть при солнце в точке Η происходит видимый вечерний восход звезды Δ. Поскольку солнце оказывается в точке Η раньше, чем в точке Γ, и в то время, когда оно в Η, происходит видимый утренний восход звезды Δ, а в то время, когда оно в Γ, происходит истинный, то получается, что видимый происходит раньше истинного.

Опять-таки, пусть некоторая неподвижная звезда заходит в точке Β, в то время как солнце заходит в точке Γ. То есть это истинный вечерний заход звезды Β. Я утверждаю, что видимый заход происходит раньше истинного.

Действительно, когда солнце заходит в точке Γ, звезда Β не видна на заходе. Не видна она на заходе и когда солнце переходит в полукруг ΓΖΑ. Таким образом, звезда Β будет видима на заходе до того, как солнце окажется в точке Γ. Пусть она будет видима в последний раз при солнце в точке Η. То есть при солнце в точке Η происходит видимый вечерний заход звезды Β. Поскольку солнце оказывается в точке Η раньше, чем в точке Γ, и в то время, когда оно в Η, происходит видимый вечерний заход звезды Β, а в то время, когда оно в Γ, происходит истинный, то получается, что видимый происходит раньше истинного.

Объявленное:

Пусть дано все то же самое.20 Я утверждаю, что звезда Δ не будет видна на восходе и тогда, когда солнце проходит дугу ΓΖΑ.21

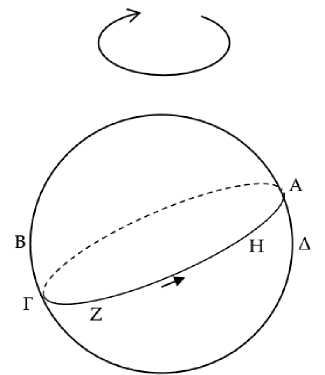
Рис. 2

Ибо пусть солнце восходит, будучи в точке Η²². Поскольку точка Η восходит раньше точки Α, а точка Α восходит вместе с Δ, то получается, что точка Η восходит раньше точки Δ. Следовательно, Δ не будет видна. Таким образом, когда солнце проходит дугу ΓΖΑ, Δ не видна на восходе.

Теорема 1.2

Всякая неподвижная звезда видна на восходе каждую ночь от ее видимого утреннего восхода и до ее видимого вечернего восхода, а в прочее время – нет. И промежуток времени, когда звезда видна на восходе, – меньше половины года.

Пусть круг ΑΒΓΔ является горизонтом космоса, а круг солнца располагается как ΑΕΓΖ (Рис. 1) . И пусть некоторая неподвижная звезда восходит в точке Δ, в то время как солнце восходит в точке Α. То есть происходит истинный утренний восход звезды Δ. Но видимые восходы происходят позже истинных.²³ Итак, пусть видимый утренний восход звезды Δ происходит при солнце в точке Ε.

Опять-таки, предположим, что, когда звезда восходит в точке Δ, солнце заходит в точке Γ. То есть происходит истинный вечерний восход звезды Δ.

Но видимые восходы происходят раньше истинных. Итак, пусть последний24 видимый вечерний восход звезды Δ происходит при солнце в точке Η. Когда солнце проходит дуги ΑΕ и ΗΓ, звезда Δ не видна на восходе. Не будет она видна на восходе и когда солнце проходит дугу ΓΖΑ25. Следовательно, звезда Δ видна на восходе только тогда, когда солнце проходит дугу ΕΗ. А промежуток времени, за который солнце проходит дугу ΕΗ, меньше половины года, так как дуга ΕΗ меньше полукруга.

Теорема 1.3

Всякая неподвижная звезда видна на заходе каждую ночь от ее видимого утреннего захода и до ее видимого вечернего восхода, а в прочее время – нет. И промежуток времени, когда звезда видна на заходе, – меньше половины года.

Пусть круг ΑΒΓΔ является горизонтом космоса, а ΑΕΓΖ – зодиак²⁶ (Рис. 1) . И пусть полукруг ΑΕΓ находится под землей, и, когда солнце восходит в точке Α, некоторая неподвижная звезда заходит в точке Β. То есть происходит истинный утренний заход звезды Β. Но видимые заходы²⁷ происходят позже истинных. Итак, пусть видимый утренний заход звезды Β впервые происходит при солнце в точке Ε.

Опять-таки, предположим, что, когда звезда Β заходит, солнце заходит в точке Γ. То есть происходит истинный вечерний заход звезды Β. Но видимые заходы28 происходят раньше истинных. Итак, пусть последний видимый вечерний заход звезды Β происходит, когда солнце находится в точке Η. Когда солнце проходит дуги ΑΕ и ΗΓ, звезда Β не видна на заходе. Не будет она видна на заходе и когда солнце проходит дугу ΓΖΑ. Следовательно, звезда Β будет видна на заходе только тогда, когда солнце проходит дугу ΕΗ.

А промежуток времени, за который солнце проходит дугу ΕΗ, меньше половины года.29

Теорема 1.4

Все неподвижные звезды, находящиеся на зодиакальном круге, совершают видимые утренние заходы через полгода после видимых утренних восходов. Те, что севернее, – через больший промежуток времени, а те, что южнее, – через меньший.

Пусть круг ΑΒΓΔ является горизонтом космоса, а круг солнца располагается как ΑΕΓΖ, и пусть полукруг ΑΕΓ находится под землей, и некоторые неподвижные звезды Β, Α, Δ восходят, когда солнце восходит в точке Α, причем Α лежит на зодиаке, Β – к северу, а Δ – к югу (Рис. 3) . Я утверждаю, что для звезды Α утренний видимый заход происходит через полгода после утреннего видимого восхода, для Β – через больший промежуток времени, а для Δ – через меньший.

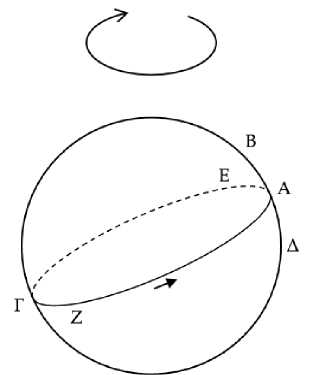
Рис. 3

Ведь когда солнце восходит в точке Α, некоторые неподвижные звезды одновременно восходят в точках Β, Α, Δ. Следовательно, это утренние истинные восходы звезд Β, Α, Δ. Но видимые утренние восходы происходят позже истинных. Итак, пусть видимые утренние восходы звезд Β, Α, Δ происходят при солнце в точке Ε. Поскольку звезды на круге зодиака, расположенные по диаметру, восходят и заходят в сопряжении³⁰, то, когда Α заходит, диаметрально противоположная ей Γ восходит, и в это время полукруг

ΑΕΓ будет над землей, а ΑΖΓ – под землей³¹. Таким образом, когда Α станет заходить, а Γ восходить, солнце окажется в точке Γ, и будет происходить истинный утренний заход звезды Α. Но видимые [утренние заходы] происходят позже истинных. Пусть же видимый утренний заход звезды Α происходит при солнце в точке Ζ. Поскольку эти звезды³² наблюдались, не затмеваемые солнечными лучами, в течение одинакового времени³³, то дуга ΑΕ равна дуге ΓΖ. Дуга же ΓΕ – общая. Следовательно, вся дуга ΑΕΓ равна всей дуге ΕΓΖ. Но ΑΕΓ есть полукруг. Следовательно, ΕΓΖ – тоже полукруг, и солнце проходит полукруг ΕΓΖ за полгода, точно так же, как и ΑΕΓ. Следовательно, для звезды Α утренний видимый заход происходит через полгода после утреннего видимого восхода. И если звезды Β, Α, Δ восходят одновременно, то Β заходит позже Α, а Δ – раньше Α.³⁴ Из этого, конечно, ясно, что Β заходит через больший, а Δ – через меньший промежуток вре- 35 мени.

Пусть круг ΑΒΓΔ является горизонтом космоса, а ΑΕΓ36 – зодиак, и пусть некоторые звезды Β, Α, Δ восходят одновременно, причем Β лежит к северу, Α – на зодиаке, а Δ – к югу (Рис. 4). Я утверждаю, что звезда Β совершает утренний видимый заход более, чем через полгода после утреннего видимого восхода, а Δ – менее.

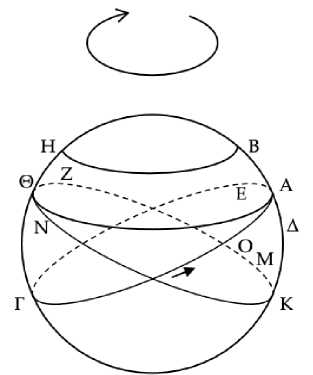
Рис. 4

Пусть ΒΗ и ΑΘ – параллельные круги, по которым движутся³⁷ Β и Α. Так как Β заходит позже Α³⁸, то Β будет над землей в то время, когда Α заходит. Но когда Α заходит, Γ восходит и круг зодиака принимает положение ΖΚΝΘ, а полукруг ΑΕΓ перейдет в ΘΝΚ и будет располагаться над землей. Дуга же ΑΕ³⁹ перейдет в дугу ΘΝ. Таким образом, при восходе Γ точка Β будет над землей. Следовательно, звезда⁴⁰, восходящая одновременно с заходом Β, расположена на дуге ΚΖΘ. Пусть это будет Μ. Таким образом, когда солнце находится в точке Μ, происходит утренний истинный заход звезды Β. Но видимые [утренние заходы] позже истинных. Следовательно, после того как солнце пройдет некоторую дугу, чтобы Β могла избежать солнечных лучей, произойдет утренний видимый заход Β. Пусть эта пройденная дуга будет ΜΟ. Значит, дуга ΘΝ равна дуге ΟΜ⁴¹. И следовательно, дуга ΟΚ

• ³⁷    В суточном вращении.

• ³⁸    В суточном вращении, см. выше, а также прим. 34.

• ³⁹    Здесь предполагается, что определение точки Ε то же, что и раньше: положение солнца, при котором три рассматриваемые звезды имеют видимый утренний восход.

• ⁴⁰    «Звезда» и «точка» являются синонимами, для Автолика не важно, наблюдается ли в этой точке реальная светящаяся звезда.

• ⁴¹    Предполагая, что время, отделяющее истинные восходы и заходы от видимых (около 15 суток), всегда одинаково. Напомним, что дуга ΘΝ есть просто ΑΕ после поворота, а Ε определено как положение солнца, при котором Β, Α, Δ имеют видимый утренний восход.

больше дуги ΘΝ. К ним добавляется общая дуга ΚΝ: таким образом, ΟΚΝ больше, чем ΚΝΘ. Но ΘΝΚ – полукруг. Следовательно, ΝΚΟ больше полукруга. Следовательно, Β совершает утренний видимый заход более, чем через полгода после утреннего видимого восхода.

И конечно, я утверждаю и то, что звезда Δ совершает утренний видимый заход менее, чем через полгода после утреннего видимого восхода.42

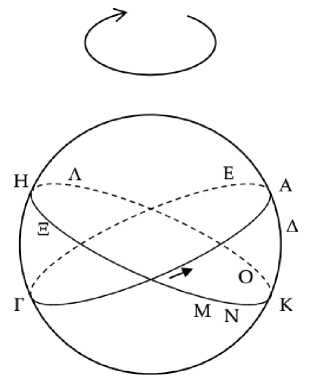
Рис. 5

Ибо поскольку Δ заходит раньше Α, при заходе Α точка Δ находится под землей (Рис. 5) . Но когда Α заходит, Γ восходит и круг зодиака принимает положение ΗΛΚΝΜ, а дуга ΑΕ – положение ΗΞ. Таким образом, при восходе Γ точка Δ находится под землей. Следовательно, звезда, восходящая одновременно с заходом Δ, расположена на дуге ΗΜΚ. Пусть это будет Ν. Таким образом, когда солнце находится в точке Ν и восходит, Δ заходит, и это будет утренний истинный заход звезды Δ. Но истинный [утренний заход] раньше видимого. Следовательно, после того как солнце пройдет некоторую дугу, чтобы Δ могла избежать солнечных лучей, произойдет утренний видимый заход Δ. Пусть эта пройденная дуга будет ΝΚΟ. Так как ΟΚΝ равна ΗΞ, дуга ΟΚ меньше, чем ΗΞ. К ним добавляется общая дуга ΚΞ: таким образом, полная дуга ΞΚΟ меньше полной дуги ΗΞΚ. Но ΚΞΗ – полукруг. Следовательно, ΞΚΟ меньше полукруга. Следовательно, солнце проходит дугу ΞΚΟ за время, меньшее половины года, так что Δ совершает утренний видимый заход менее, чем через полгода после утреннего видимого восхода.

Теорема 1.5

Все неподвижные звезды, находящиеся на круге зодиака, совершают видимые вечерние заходы через полгода после видимых вечерних восходов. Те, что севернее, – через больший промежуток времени, а те, что южнее, – через меньший.

Пусть круг ΑΒΓΔ является горизонтом космоса (Рис. 6) , а круг солнца располагается как ΑΕΓΖ, и пусть полукруг ΑΕΓ находится под землей и некоторые неподвижные звезды Β, Α, Δ восходят, в то время как солнце заходит в точке Γ, причем Α лежит на зодиаке, Β – к северу, а Δ – к югу. Я утверждаю, что для звезды Α вечерний видимый заход происходит через полгода после вечернего видимого восхода, для Β – через больший промежуток времени, а для Δ – через меньший.

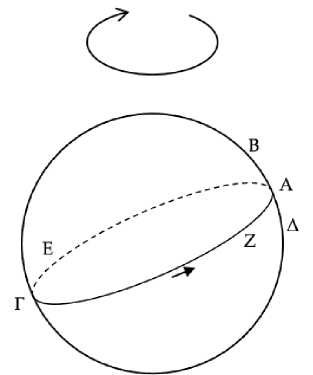
Рис. 6

Действительно, поскольку при заходе солнца в точке Γ восходят некоторые неподвижные звезды Β, Α, Δ, то происходит истинный вечерний восход звезд Β, Α, Δ. Но видимый [утренний восход] раньше истинного. Так пусть же вечерние видимые восходы звезд Β, Α, Δ происходят при солнце в точке Ε. Опять-таки, поскольку звезды на круге зодиака, расположенные по диаметру, восходят и заходят в сопряжении⁴³, то, когда Γ восходит, диаметрально противоположная ей Α заходит, так что при восходе звезды Γ солнце, находясь в точке Α, будет заходить. И звезда Α будет заходить вместе с солнцем, и это будет вечерний истинный заход звезды Α. Но видимый [вечерний заход] раньше истинного. Так пусть же видимый вечерний заход Α происходит при солнце в точке Ζ. То есть дуга ΓΕ равна дуге ΑΖ. И тем же

• ⁴³    См. прим. 30.

способом44 получается, что для звезды Α вечерний видимый заход наступит через полгода после вечернего видимого восхода. И ясно, что для Β промежуток времени больше, а для Δ – меньше.

Теорема 1.6

Всякая неподвижная звезда, совершающая восходы и заходы⁴⁵, восходит вместе с солнцем приблизительно раз в год, совершая истинный утренний восход. Таким же образом она и заходит вместе с солнцем.⁴⁶

Пусть круг ΑΒΓΔ является горизонтом космоса, а круг солнца располагается как ΑΕΓΖ, и пусть некоторая неподвижная звезда Δ восходит, в то время как солнце восходит в точке Α (Рис. 7) . Следовательно, это истинный утренний восход звезды Δ. Так вот, я утверждаю, что звезда Δ восходит вместе с солнцем приблизительно раз в год.

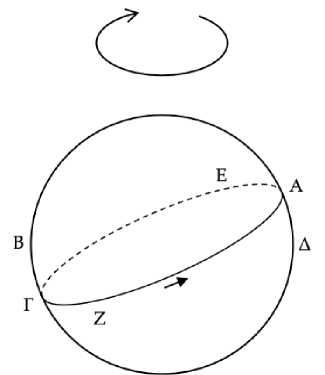
Рис. 7

Итак, если солнце, взойдя в точке Α, проходит ΑΕΓΖ за целое число об-ращений⁴⁷, то очевидно, что звезда Δ взойдет вместе с солнцем через год.

Если же вдобавок к целому числу есть и некоторая часть обращения, то возникнет небольшое расхождение, приводящее к тому, что звезда Δ не будет восходить вместе с солнцем. Ведь всякая из неподвижных звезд становится видна, избегая солнечных лучей, через пятнадцать обращений48, а год образуется из целого числа обращений солнца и одной четверти49. Следовательно, утренний истинный восход звезды Δ наступит приблизительно через один год, так что всякая неподвижная звезда, совершающая восходы и заходы, восходит вместе с солнцем приблизительно раз в год, совершая истинный утренний восход. Аналогично может быть показано и то, что она так же заходит вместе с солнцем.

Теорема 1.7

Всякая неподвижная звезда совершает вечерний истинный восход приблизительно через полгода после утреннего истинного восхода, а утренний истинный заход – приблизительно через полгода после вечернего истинного захода.50

Пусть круг ΑΒΓΔ является горизонтом космосa (Рис. 7) , а круг солнца располагается как ΑΕΓΖ, и пусть некоторая неподвижная звезда Δ восходит, в то время как солнце восходит в точке Α. Таким образом, это истинный утренний восход звезды Δ. Я утверждаю, что вечерний истинный восход звезды Δ происходит приблизительно через полгода после ее утреннего истинного восхода.

Действительно, если солнце проходит дугу ΑΕΓ за целое число дней51, то очевидно, что оно зайдет в точке Γ, и вечерний истинный восход звезды Δ произойдет через полгода. Если же солнце проходит дугу ΑΕΓ не за целое число дней, то возникнет небольшое расхождение, приводящее к тому, что солнце не будет заходить вместе со звездой Δ, так что для звезды Δ вечерний истинный восход произойдет приблизительно через полгода после утреннего истинного восхода.

Аналогичным образом покажем, разумеется, и то, что звезда совершает утренний истинный заход [приблизительно] через полгода после истинного вечернего захода.

Теорема 1.8

Все звезды, которые находятся на круге зодиака, совершают первое утреннее появление52 после последнего вечернего появления53, пробыв невидимыми в течение скольких-то54 дней и ночей.

Пусть круг ΑΒΓΔ является горизонтом космоса (Рис. 8) , а круг солнца располагается как ΑΕΓ, и пусть солнце проходит часть ΓΕΑ, точка же Ε пусть будет некоторая неподвижная звезда, расположенная на круге зодиака. И пусть солнечные лучи⁵⁵ в последний раз настигают звезду Ε при солнце в точке Ζ, а при солнце в точке Η эта звезда впервые избегает солнечных лучей⁵⁶. То есть пусть последнее вечернее появление звезды Ε будет при солнце в точке Ζ, а первое утреннее появление – при солнце в точке Η. Я утверждаю, что, пока солнце проходит дугу ΖΗ, звезда Ε не видна.

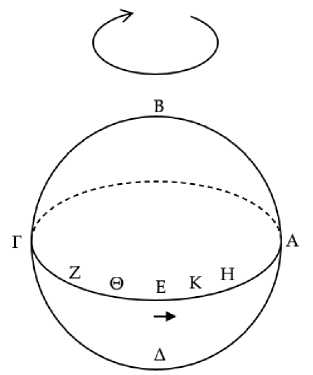
Рис. 8

Ибо пусть солнце находится в точке Θ.⁵⁷ Следовательно, при солнце в точке Θ звезда Ε не видна на восходе: ведь точка Θ, то есть солнце, восходит раньше ее. Нельзя будет ее наблюдать и на заходе, поскольку последнее вечернее появление звезды Ε происходит при солнце в точке Ζ. Таким образом, при солнце в точке Θ звезда Ε не видна.

Аналогичным образом покажем, разумеется, и то, что звезда Ε не видна, когда солнце проходит дугу ΖΕ.58

Далее, я утверждаю, что невидима она и тогда, когда солнце проходит дугу ΕΗ. Ибо пусть солнце находится в точке Κ.59 Получается, что при солнце в точке Κ звезда Ε невидима на заходе: ведь точка Ε заходит прежде точки Κ, то есть солнца. Нельзя будет ее наблюдать и на восходе, поскольку первое утреннее появление звезды Ε происходит при солнце в точке Η. Таким образом, при солнце в точке Κ звезда Ε не видна.

Аналогичным образом покажем, разумеется, и то, что звезда Ε невидима, когда солнце проходит дугу ΕΗ.60 Но это же было показано и для дуги ΖΕ. Следовательно, звезда Ε не видна, пока солнце проходит всю дугу ΖΕΗ.

Теорема 1.9

Звезды, расположенные южнее круга зодиака, совершают первое утреннее появление61 после последнего вечернего появления62, пробыв невидимыми в течение большего числа дней, чем звезды на круге зодиака.

Пусть круг ΑΒΓ является горизонтом космоса, ΑΔΕ – наибольший из [кругов], которые всегда видимы⁶³, а круг солнца располагается как ΒΖΓ (Рис. 9) . И пусть точка Η будет некоторая неподвижная звезда, расположенная южнее круга зодиака. Я утверждаю, что звезда Η совершает первое утреннее появление, пробыв невидимой после последнего вечернего появления в течение большего числа дней, чем звезды на круге зодиака.

Рис. 9

Ибо пусть через точку Η проведен большой круг64 ΛΗΔΜ, касающийся круга ΑΔΕ, так что полукруг, начинающийся от точки Δ и содержащий часть ΔΗ, не пересекается с полукругом, начинающимся от точки Α и содержащим часть ΑΜΒ. Пусть Ζ будет некоторая звезда на круге зодиака65, и пусть лучи солнца в последний раз настигают66 звезду Ζ при солнце в точке Θ, а при солнце в точке Κ эта звезда впервые избегает67 солнечных лучей. Следовательно, пока солнце проходит дугу ΘΚ, звезда Ζ невидима.68 И поскольку звезды Ζ и Η заходят одновременно (ведь полукруг, начинающийся от точки Δ и содержащий часть ΔΗ, не пересекается с полукругом, начинающимся от точки Α и содержащим часть ΑΒ)69, Ζ и Η совместно попадают в лучи солнца. А последнее вечернее появление звезды Ζ происходит при солнце в точке Θ. Следовательно, при солнце в точке Θ происходит также и последнее вечернее появление звезды Η. Однако, поскольку Ζ и Η одновременно заходят, но не одновременно восходят (Ζ восходит раньше Η)70, то ясно, что звезда Ζ начинает избегать солнечных лучей раньше. А первое утреннее появление звезды Ζ происходит при солнце в точке Κ. Следовательно, при солнце в точке Κ звезда Η еще не избегает лучей солнца. Значит, звезда Η совершает первое утреннее появление, пробыв невидимой после последнего вечернего появления в течение большего числа дней, нежели звезды на круге зодиака.

Теорема 1.1071

Некоторые из неподвижных звезд, совершающих восходы и заходы72 и расположенных к северу от круга зодиака, видны каждую ночь.

Пусть круг ΑΒΓ является горизонтом космоса, ΑΔΕ – наибольший из [кругов], которые всегда видимы, а ΒΖΓ – зодиак (Рис. 10) . И пусть, в то время как солнце находится в точке Ζ, точки Η и Θ будут некоторые звезды⁷³, такие, что, когда Η впервые избегает солнечных лучей, лучи в последний раз настигают Θ.⁷⁴ То есть, когда⁷⁵ у звезды Η происходит утренний видимый восход, у звезды Θ происходит вечерний видимый заход. И пусть через точки Η и Θ проведены большие круги ΛΗΚΕ и ΜΘΚΔ, касающиеся круга ΑΔΕ. Пусть они проведены так, что полукруг ΕΗΛ не пересекается с полукругом, начинающимся от точки Α и идущим к точке Γ, а полукруг ΔΘΜ⁷⁶ не пересекается с полукругом, начинающимся от точки Α и идущим к точке Β. То есть они проведены так, что полукруг ΗΕ накладывается на восход, а

ΘΔ – на заход.77 А точка Κ пусть будет некоторая звезда, расположенная ближе к северу. Так вот, я утверждаю, что звезда Κ видна каждую ночь.78

Рис. 10

Ибо положим79, что дуга ΛΝ равна ΖΗ, а дуга ΜΞ равна ΖΘ. Разумеется, ΜΞ будет также равна и ΛΝ, поскольку ΖΘ равна ΖΗ в силу предположения, что звезды избегают лучей солнца в течение равного времени. И поскольку точка Η диаметрально противоположна точке Λ, а утренний видимый восход звезды Η происходит при солнце в точке Ζ, то получается, что вечерний видимый восход звезды Η будет происходить при солнце в точке Ν, в силу равенства дуг ΖΗ и ΛΝ. И то время, в течение которого солнце проходит дугу ΖΓΝ, будет для звезды Η временем от утреннего видимого восхода и до вечернего видимого восхода. Таким же образом, поскольку точка Θ диаметрально противоположна точке Μ, а дуга ΖΘ равна дуге ΜΞ, а вечерний видимый заход звезды Θ происходит при солнце в точке Ζ, то получается, что утренний видимый заход звезды Θ будет происходить при солнце в точке Ξ. И то время, в течение которого солнце проходит дугу ΞΒΖ, будет для звезды Θ временем от утреннего видимого захода и до вечернего видимого захода. Но поскольку было доказано80, что всякая неподвижная звезда видна на восходе каждую ночь от утреннего видимого восхода и до вечернего видимого восхода, то звезда Η, следовательно, видна на восходе каждую ночь, пока солнце проходит дугу ΖΓΝ. Но Η восходит одновременно с Κ.81 Следовательно, и Κ будет видна на восходе каждую ночь, пока солнце проходит дугу ΖΓΝ. Таким же образом, поскольку всякая неподвижная звезда видна на заходе каждую ночь от утреннего видимого захода и до вечернего видимого захода82, то, пока солнце проходит дугу ΞΒΖ, звезда Θ будет, следовательно, видима на заходе. Но звезда Θ заходит одновременно с Κ. Следовательно, и Κ будет видима на заходе, пока солнце проходит дугу ΞΒΖ. Таким образом, звезда Κ будет видима каждую ночь на заходе, когда солнце проходит дугу ΞΒΖ, и на восходе – когда оно проходит дугу ΖΓΝ.

И ясно, что звезда Κ будет видима на заходе или на восходе83, пока солнце проходит дугу ΞΒΖΓΝ. Далее, я утверждаю, что звезда Κ будет видна каждую ночь и в то время, когда солнце проходит дугу ΝΜΞ.

Ибо предположим, что дуга ΒΗ равна дуге ΓΘ.84 Тогда и ΓΛ равна ΒΜ, так что и ΓΝ равна ΒΞ. Также, дуги ΒΞ и ΓΝ больше, чем ΗΖ и ΖΘ, соответ- ственно.85 А звезды могут избежать лучей солнца, когда оно находится под землей, отстоя от горизонта на величину большей дуги.86 Таким образом, при том положении, которое теперь занимает круг зодиака, все звезды, лежащие на дуге ΒΖΓ, видимы, пока солнце проходит дугу ΝΜΞ.87 Следовательно, будет видима и звезда Κ.88 Следовательно, звезда Κ будет видна каждую ночь.

А то, что дуги ΒΞ и ΓΝ больше, чем ΗΖ и ΖΘ, соответственно, – это ясно. Ведь каждая из дуг ΗΖ и ΖΘ составляет половину знака зодиака89. Таким образом, ΗΘ равна знаку зодиака, как и ΛΜ. Следовательно, ΝΜΞ равна двум знакам зодиака. Рассматривая остаток, получаем, что каждая из дуг ΗΞ и ΘΝ равна четырем с половиной знакам зодиака.90 И в той и в другой ΒΗ и ΘΓ составляют по два с половиной знака зодиака.91 Следовательно, обе остающиеся дуги, ΒΞ и ΓΝ, составляют по два знака зодиака, так что ΒΞ и ΓΝ больше, чем ΗΖ и ΖΘ, соответственно.

Теорема 1.11

Ни одна из расположенных на круге зодиака звезд не будет видна на протяжении их движения через всю видимую полусферу, и то же верно и для звезд, расположенных севернее. Все же звезды, которые расположены южнее и не совсем уж близко к кругу зодиака, могут92 быть видимы на протяжении их движения через всю видимую полусферу.

Пусть круг ΑΒΓΔ является горизонтом космоса, а ΔΒΕ – зодиак. И пусть Α, Δ и Γ будут некоторые неподвижные звезды на восходе, причем Δ лежит на круге зодиака, Α – к северу от него, а Γ – к югу (Рис. 11) . Я утверждаю, что ни Δ, ни Α не будут видны на протяжении их движения через всю видимую полусферу, а некоторые звезды из лежащих дальше к югу, такие как Γ, могут быть видны на протяжении их движения через всю видимую полусферу.

Рис. 11

Ибо пусть полукруг ΔΕΒ находится под землей, и звезды Α, Δ и Γ видны на восходе при солнце в точке Ε. Поскольку звезды на круге зодиака, расположенные по диаметру, восходят и заходят в сопряжении,⁹³ то, когда Δ заходит, диаметрально противоположная ей Β восходит и полукруг ΔΕΒ приходит в надземное положение. Следовательно, звезда Δ заходит днем.⁹⁴ Следовательно, звезда Δ не будет видна на протяжении ее движения через всю видимую полусферу. И так как звезды Α и Δ восходят одновременно, а Α лежит дальше к северу, то Α заходит позже Δ.⁹⁵ Но Δ заходит днем. Следовательно, и Α будет заходить днем⁹⁶, так что звезда Α не будет видна на протяжении ее движения через всю видимую полусферу. Опять-таки, поскольку

Γ и Δ восходят одновременно, то Δ заходит позже Γ97, так что оказывается возможным взять некоторые звезды, расположенные к югу, которые видимы на протяжении их движения через всю видимую полусферу. Ведь они будут описывать круги, такие как ΓΗ, и расположенная над землей дуга ΓΗ этого круга будет меньше98 либо подобна заданной дуге параллельного круга, по которой перемещается солнце за то время, пока восходит дуга ΕΔ зо-диака.99

Теорема 1.12

Те звезды, у которых утренний истинный заход происходит после утреннего истинного восхода спустя время, меньшее половины года,100 будут заходить и восходить при солнце под землей в течение того промежутка времени, которого им недостает до половины года. А в течение другого, равного промежутка времени, они не будут ни заходить, ни восходить при солнце под землей.

Пусть круг ΑΒΓΔ является горизонтом космоса, а круг солнца располагается как ΑΕΓΖ, и пусть некоторая расположенная к югу [от круга солнца] звезда Δ восходит, в то время как солнце восходит в точке Α (Рис. 12) . Таким образом, для звезды Δ утренний истинный заход происходит после утреннего истинного восхода спустя время, меньшее, чем полгода.¹⁰¹ И вот, я утверждаю, что в течение этого промежутка времени, которого недостает до половины года, звезда Δ будет и заходить, и восходить при солнце под землей. А в течение другого, равного промежутка времени, звезда Δ не будет ни заходить, ни восходить при солнце под землей.

См. прим. 100.

Теорема 9 из сочинения Автолика «О движущейся сфере», ср. прим. 34.

Здесь проявилось то, что Автолик, обозначив некую точку на горизонте, мо-

Рис. 12

Ибо пусть истинный утренний заход звезды Δ происходит при солнце в точке Ε.102 Следовательно, время, за которое солнце проходит дугу ΑΕ, начиная от утреннего истинного восхода, есть время до утреннего истинного захода звезды Δ. Следовательно, тот промежуток времени, которого этому времени недостает до половины года, есть то время, за которое солнце проходит дугу ΓΕ. А поскольку при восходе звезды Δ в точке Δ103 круг зодиа- жет понимать под ней две разные вещи: 1) неподвижную точку горизонта и 2) звезду, в рассматриваемый момент времени находящуюся в этой точке в ходе суточного вращения неба. Поэтому выражение «при восходе звезды Δ в точке Δ» имеет смысл.

ка всегда занимает одно и то же положение104 и полукругом под землей является ΑΕΓ, а остатком над землей – ΓΖΑ, то оказывается, что если Δ восходит, а солнце проходит дугу ΑΕΓ, то оно проходит ее под землей. Это относится и к дуге ΓΕ. Следовательно, звезда Δ восходит, когда солнце, проходя дугу ΓΕ, находится под землей, пусть даже эта звезда при этом и не видима на восходе.105 Теперь предположим, что дуга ΑΖ противоположна и равна дуге ΕΓ. Поскольку утренний истинный заход звезды Δ происходит при солнце в точке Ε, то очевидно, что при заходе Δ солнце восходит в точке Ε и полукруг ΕΓΖ еще находится под землей, а ΖΑΕ – это то, что остается над землей. С другой стороны, если Δ заходит, а солнце проходит дугу ΕΓΖ, то оно проходит ее под землей.106 Это относится и к дуге ΕΓ. Следовательно, звезда Δ заходит, когда солнце, проходя дугу ΕΓ, находится под землей. Было, однако же, показано, что, когда солнце, проходя дугу ΕΓ, находится под землей, звезда Δ восходит. Следовательно, когда солнце, проходя дугу ΕΓ, находится под землей, звезда Δ и заходит, и восходит.

Далее, я утверждаю, что, когда солнце проходит под землей дугу ΖΑ, звезда Δ ни заходит, ни восходит при солнце под землей.107

Ведь поскольку при восходе звезды Δ полукруг ΑΕΓ находится под землей, а ΓΖΑ – над землей, то оказывается, что если Δ восходит, а солнце проходит дугу ΓΖΑ, то оно проходит ее над землей. Это относится и к дуге ΖΑ. Следовательно, звезда Δ восходит, когда солнце, проходя дугу ΖΑ, находится над землей. И опять-таки, поскольку при заходе Δ полукруг ΖΑΕ находится над землей, а ΕΓΖ – под землей, то получается, что если Δ заходит, а солнце проходит дугу ΖΑΕ, то оно проходит ее над землей. Это относится и к дуге ΖΑ. Следовательно, звезда Δ и заходит, и восходит, когда солнце проходит дугу ΖΑ над землей. Таким образом, когда солнце проходит дугу ΖΑ под землей, звезда Δ ни заходит, ни восходит.

Теорема 1.13

Те звезды, у которых утренний истинный заход происходит после утреннего истинного восхода спустя время, большее половины года, 108 не будут ни заходить, ни восходить при солнце под землей в течение того промежутка времени, на который это их время превышает половину года. А в течение другого, равного промежутка времени, они будут и заходить, и восходить при солнце под землей.

Пусть круг ΑΒΓΔ является горизонтом космоса, а круг солнца располагается как ΑΕΓΖ, а полукругом по землей пусть будет ΑΕΓ (Рис. 13) . И пусть некоторые неподвижные звезды Α, Β и Δ восходят, в то время как солнце восходит в точке Α. И пусть Β расположена к северу [от круга солнца]. Таким образом, для звезды Β утренний истинный заход происходит после утреннего истинного восхода спустя время, большее, чем полгода.¹⁰⁹ И вот, я утверждаю, что в течение того промежутка времени, на который это время превышает половину года, звезда Β не будет ни заходить, ни восходить при солнце под землей. А в течение другого, равного промежутка времени, звезда Β будет и заходить, и восходить при солнце под землей.

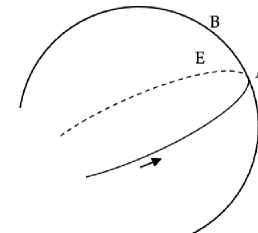
Рис. 13

Ибо пусть истинный утренний заход звезды Β происходит, когда солнце прошло дугу ΑΕΓΖ и находится в точке Ζ. Следовательно, тот промежуток времени, на который превышена половина года, есть то время, за которое солнце проходит дугу ΓΖ. Я утверждаю, что, когда солнце, проходя дугу ΓΖ, находится под землей, звезда Β не будет ни заходить, ни восходить.

Ведь поскольку, когда Β восходит, полукруг ΑΕΓ находится под землей, а ΓΖΑ – над землей, то оказывается, что если Β восходит, а солнце проходит дугу ΓΖΑ, то оно проходит ее над землей. Это касается и дуги ΓΖ. Следовательно, когда солнце, проходя дугу ΓΖ, находится над землей, звезда Β восходит, хотя и не видима на восходе.110 Теперь предположим, что дуга ΑΕ равна и противоположна дуге ΓΖ. Поскольку истинный утренний заход звезды Β происходит при солнце в точке Ζ, то, следовательно, при заходе Β солнце восходит в точке Ζ. Но когда точка Ζ восходит, точка Ε заходит. И полукруг ΕΓΖ будет над землей, а ΖΑΕ – под землей. С другой стороны, если Β заходит, а солнце проходит дугу ΕΓΖ, то оно проходит ее над землей. Это относится и к дуге ΓΖ. Следовательно, когда солнце, проходя дугу ΓΖ, находится над землей, звезда Β заходит, хотя она и не видна. Следовательно, когда солнце, проходя дугу ΓΖ, находится над землей, звезда Β и заходит, и восходит. Таким образом, когда солнце, проходя дугу ΓΖ, находится под землей, звезда Β ни заходит, ни восходит.

Далее, я утверждаю, что, когда солнце, проходя дугу ΑΕ, находится под землей, звезда Β будет и заходить, и восходить. Ведь поскольку при восходе звезды Β полукруг ΑΕΓ находится под землей, а ΓΖΑ – над землей, то оказывается, что, если Β восходит, а солнце проходит дугу ΑΕΓ, то оно проходит ее под землей. Это относится и к дуге ΑΕ. Опять-таки, поскольку при заходе Β полукруг ΖΑΕ находится под землей, а ΖΓΕ – над землей, то получается, что, если Β заходит, а солнце проходит дугу ΖΑΕ, то оно проходит ее под землей. Это относится и к дуге ΑΕ. Следовательно, когда солнце, проходя дугу ΑΕ, находится под землей, звезда Β будет и заходить, и восходить.

Книга вторая

Теорема 2.1

Одна двенадцатая часть111 зодиака, в которой находится солнце, не видна ни на восходе, ни на заходе, но вращается, будучи скрытой. Сходным образом, диаметрально противоположная ей часть не показывается ни на восходе, ни на заходе, но остается видимой над землей в течение всей ночи.

Пусть АВ является кругом зодиака, а ГА - горизонтом, и пусть восход солнца происходит в точке А, а закат - в точке Г (Рис. 14) . И пусть космос вращается от восхода А к закату Г, а солнце движется навстречу зодиаку¹¹², а дуга АЕ равна одному знаку¹¹³ зодиака и разделена пополам точкой Z.¹¹⁴ Я утверждаю, что дуга ЕА не видна ни на восходе, ни на заходе, как и диаметрально противоположная ей дуга, которая совершает всю надземную часть вращения, будучи видимой, когда солнце находится под землей.

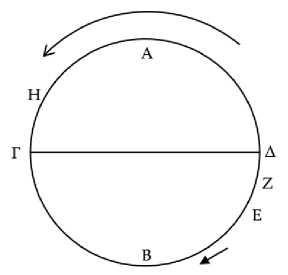
Рис. 14

Ведь поскольку предполагается, что звезды избегают лучей солнца, если солнце находится под землей, отстоя от горизонта на половину знака зодиака, а дуга ΖΔ составляет половину знака зодиака, то получается, что при солнце в точке Ζ звезда Δ совершает утренний видимый восход. Следовательно, дуга ΖΔ не видна на восходе ночью. Ясно и то, что и дуга ΖΕ не видна на восходе.115 Следовательно, вся дуга ΕΔ не видна на восходе. Такими же рассуждениями получим, разумеется, что дуга вся ΕΔ не видна и на заходе, когда солнце находится в точке Ζ,116 и то же верно для диаметрально противоположной ей дуги ΓΗ. Ведь при восходе дуги ΕΔ диаметрально противоположная ей дуга ΓΗ заходит, а при заходе дуги ΕΔ диаметрально противоположная ей дуга восходит. Следовательно, дуга ΕΔ не видна ни на восходе, ни на заходе, и то же верно для диаметрально противоположной ей дуги, которая совершает всю надземную часть вращения, будучи видимой.117

Теорема 2.2

Среди двенадцати знаков зодиака, предшествующий тому, в котором находится солнце, видим утром на восходе, а последующий118 – вечером на заходе.119

Пусть ΑΒ является кругом зодиака, а ΓΔ – горизонтом. И пусть дуга ΕΔ составляет одну двенадцатую часть, и солнце находится в ее середине (Рис. 15). Пусть ΔΗ будет следующая за солнцем двенадцатая часть, а ΕΘ – пред- шествующая ему. Я утверждаю, что дуга ΔΗ совершает утренний восход120, а дуга ΕΘ – вечерний заход.

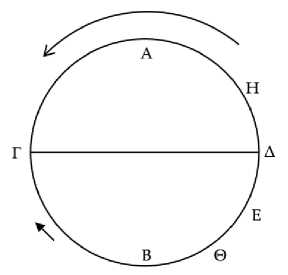
Рис. 15

Ибо дуга ΔΗ, отстоя [от солнца] более, чем на половину знака зодиака, видна на восходе, совершая, таким образом, утренний восход. Дуга же ΔΕ не видна на восходе, а дуга ΕΘ не видна, поскольку восходит днем. По мере того, как космос вращается, дуга ΔΗ совершает утренний восход, дуга ΔΕ не видна при восходе, а дуга ΕΘ, отстоя [от солнца] более, чем на половину знака зодиака, видима на заходе. Таким образом, ΕΘ совершает вечерний заход, а ΔΗ – утренний восход.

Теорема 2.3

В ночное время наблюдаема дуга из одиннадцати знаков зодиака. Из них шесть – ранее взошедшие, а пять – восходящие.121

Пусть ΑΒ является кругом зодиака, а ΓΔ – горизонтом. И пусть дуга ΓΕ составляет один знак зодиака, и солнце находится в ее середине, в точке Ζ (Рис. 16) .

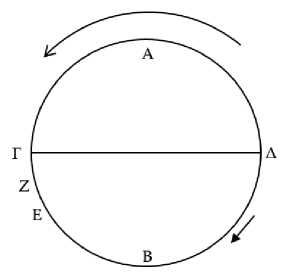
Рис. 16

Поскольку предполагается, что звезды избегают лучей солнца, когда оно находится в положении Ζ, то ясно, что звезда Γ совершает вечерний видимый заход. Весь полукруг ΓΑΔ составляет шесть знаков зодиака, так что остальные шесть знаков помещаются в полукруге ΓΒΔ, причем один из них занимает дугу ΓΕ, содержащую солнце, а остальные пять – восходящие. Таким образом, видимы одиннадцать знаков зодиака.

Теорема 2.4

Все те неподвижные звезды, которые зодиак отделяет либо в северную, либо в южную часть [неба]122, переходят от утреннего восхода к вечернему восходу123 за пять месяцев.

Пусть ΑΒ является горизонтом, разделяющим видимое и невидимое,124 и пусть ΓΔ и ΕΖ будут тропики125, ΗΘ – круг равноденствия126, а ΚΗΛΘ – круг зодиака (Рис. 17). И пусть Μ, Θ и Ν будут три звезды на восходе. Я утверждаю, что звезды Μ, Θ и Ν переходят от утреннего восхода к вечернему восходу за пять месяцев.

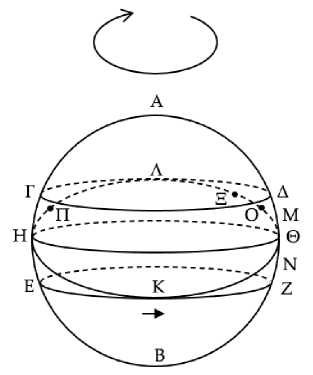
Рис. 17

Ибо пусть дуга ΘΞ заключает в себе один знак зодиака и делится пополам точкой Ο, а в точке Ο пусть находится солнце. Разумеется, в этот момент Μ, Θ и Ν совершают утренний восход. Пусть же солнце, двигаясь навстречу знакам зодиака,¹²⁷ переместится на пять знаков¹²⁸ зодиака и окажется в положении Π. Итак, от точки Ο солнце прошло дугу в пять знаков зодиака, а от точки Η отстоит на дугу в половину знака.¹²⁹ А когда точка Η заходит, звезды Μ, Θ и Ν совершают вечерний восход, после того как они совершали утренний восход.

• ¹²⁵    То есть параллельные круги (их ось – ось суточного вращения неба), которые касаются эклиптики.

• ¹²⁶    Небесный экватор. На самом деле, ни экватор, ни тропики не требуются для доказательства. Очевидно, они добавлены просто для полноты картины.

• ¹²⁷    Навстречу их суточному движению, то есть противоположно суточному вращению неба.

• ¹²⁸    Что занимает пять месяцев. Автолик отвлекается от календарных деталей, «месяц» есть просто 1/12 часть года.

• ¹²⁹    Что означает, что заход точки Η, как и одновременный ему восход звезд Μ, Θ и Ν, будет видим.

Теорема 2.5130

Для тех, кто живет в северной зоне131, всякая неподвижная звезда совершает восходы и заходы132, как вечерние, так и утренние, через промежутки времени в один год.

Пусть АВ является горизонтом, и пусть ГА и EZ будут тропики, Н0 -круг равноденствия, а КНЛ0 - круг зодиака (Рис. 18) . И пусть М будет некоторая звезда, расположенная севернее¹³³. Я утверждаю, что звезда М перейдет от утреннего восхода к утреннему восходу за один год.

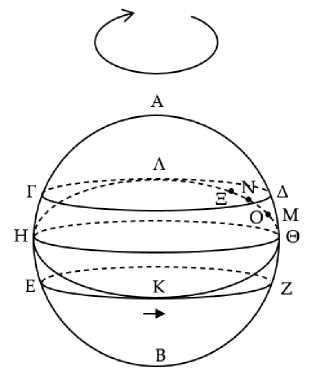
Рис. 18

Ибо пусть дуга ΘΝ заключает в себе половину знака зодиака, и звезда Θ восходит, когда солнце оказывается в точке Ν. К следующей ночи, пусть [солнце] пройдет дугу ΝΞ, и пусть дуга ΟΘ равна дуге ΝΞ. Прибавим к обеим общую дугу ΝΟ. Следовательно, вся дуга ΞΟ равна всей дуге ΝΘ. Но ΝΘ есть половина знака зодиака. Следовательно, и дуга ΞΟ есть половина знака зодиака.¹³⁴ И поскольку Θ восходит прежде Ο, а Μ восходит одновременно с Θ, то Μ восходит прежде Ο.¹³⁵ И так будет всегда, пока солнце, пройдя всю дугу ΝΛΗΚΘΝ¹³⁶, не прибудет в точку Ν. Таким образом, звезда Μ перейдет

• ¹³⁴    Смысл рассмотрения следующей ночи и введения точек Ξ и Ο следующий: поскольку ΞΟ равна половине знака зодиака, то при солнце в точке Ξ («следующая ночь») гелиакически восходят звезды, восходящие уже одновременно с точкой Ο, а не одновременно с точкой Θ, как это делает звезда Μ. Следовательно, восход Μ, конечно, видим, но он уже не гелиакический.

• ¹³⁵    Точка Ο в этой фразе (дважды) – наша эмендация. В тексте вместо этого Ν, что не имеет смысла: в таком виде это очевидное утверждение, никак не связанное с предшествующим рассуждением и никак не приближающее нас к доказываемому. Мы исходим из следующей логики: Автолик только что доказал, что «утренний видимый восход» при солнце в точке Ξ совершает точка Ο, а следовательно, и все звезды, восходящие одновременно с Ο. Теперь он указывает, что Μ восходит раньше Ο (до тех пор, пока солнце не вернется в Ν), так что Μ более не совершает «утренний видимый восход». Ср. также вторую часть доказательства, построенную именно таким образом: «Ξ восходит прежде Ρ…» (а не «прежде Ο»), а заодно и доказательство следующей теоремы, где содержится полностью аналогичное построение.

• ¹³⁶    То есть совершит полный круг по эклиптике.

от утреннего восхода к утреннему восходу за один год. То же самое будет и с вечерним восходом.

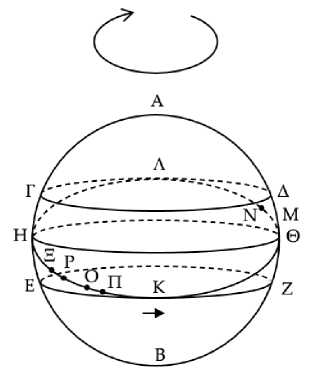
Рис. 19

Опять-таки, при тех же предположениях, поскольку звезда Μ севернее Θ и восходит одновременно с ней, то зайдет она не одновременно с ней.¹³⁷ Таким образом, Μ зайдет одновременно с какой-то точкой, следующей¹³⁸ за Θ. Пусть одновременно с ней заходит точка Ν (Рис. 19) , и пусть точка Ξ диаметрально противоположна Ν, а дуга ΞΟ пусть будет равна половине знака зодиака. Следовательно, когда солнце оказывается в точке Ο, звезда Ξ восходит утром, звезда же Ν заходит утром.¹³⁹ Следовательно, и звезда Μ заходит утром. Пусть солнце в течение дня пройдет дугу ΟΠ, и пусть ΡΞ равна ΠΟ. Прибавим к ним общую дугу ΡΟ. Следовательно, ΞΟ равна всей дуге ΡΠ. Но дуга ΞΟ есть половина знака зодиака. Следовательно, и дуга ΡΠ есть половина знака зодиака. Следовательно, при солнце в точке Π точка Ρ восходит утром. А Ξ восходит прежде Ρ, и когда Ξ восходит, Ν заходит утром, а Μ заходит одновременно с ней. Следовательно, Μ не¹⁴⁰ заходит утром при солнце в точке Π. И так будет всегда, пока солнце, обойдя полный круг, не придет в точку Ο через год. То же самое будет и с вечерним заходом.

Теорема 2.6

Всякая расположенная на зодиаке звезда переходит от утреннего восхо-да141 к вечернему восходу, а от вечернего восхода к утреннему заходу, а от утреннего захода к вечернему заходу, а от вечернего захода к утреннему восходу. И от вечернего захода к утреннему восходу она переходит за тридцать дней, причем в течение этого времени она не видна ни на восходе, ни на заходе. От утреннего же восхода к вечернему восходу она переходит за пять месяцев, и в течение этого времени она наблюдаема на восходе. От вечернего же восхода к утреннему заходу она перейдет через тридцать дней и не видима ни на восходе, ни на заходе. От утреннего же захода к вечернему заходу она переходит за пять месяцев, и в течение этого времени она видна на заходе.

Пусть ΑΒ является горизонтом, разделяющим видимое и невидимое на сфере, ΓΔ – зодиаком, а Δ – некоторой звездой на восходе. И пусть дуга ΔΕ составляет половину знака зодиака, и то же дуги ΖΓ, ΓΗ и ΘΔ (Рис. 20) .

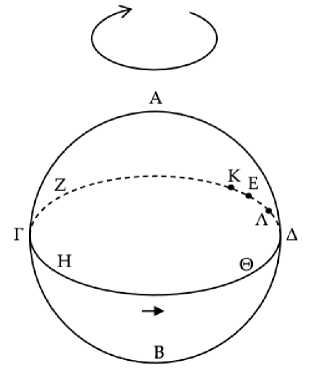
Рис. 20

Конечно, ясно, что при солнце в точке Ε звезда Δ совершает утренний восход. Пусть же ΕΚ – дуга, которую солнце проходит за ночь, и выберем ΔΛ равной ΕΚ, а дуга ΛΕ у них общая. Следовательно, вся дуга ΔΕ равна всей дуге ΛΚ. Но ΔΕ есть половина знака зодиака. Следовательно, ΛΚ – тоже половина. Следовательно, при солнце в точке Κ звезда Λ видна утром на восходе. А Δ восходит раньше ее.142 И так будет всегда, пока солнце не при- дет в точку Ζ. И когда оно оказывается в точке Ζ и отстоит143 на половину знака зодиака (дуга ΓΖ), звезда Δ совершает вечерний восход. Следовательно, звезда Δ переходит от утреннего восхода к вечернему восходу за пять месяцев: ведь дуга ΕΖ составляет пять знаков зодиака, и ясно, что пять знаков зодиака проходятся за пять месяцев.

Разумеется, подобным же образом будет доказано и все остальное в формулировке теоремы. Ведь когда солнце пройдет вдоль дуги ΖΓΗ, которая составляет один знак зодиака, произойдет утренний заход звезды Δ, и ясно, что это будет через тридцать дней. Далее, когда оно пройдет дугу ΗΘ, составляющую пять знаков зодиака, произойдет вечерний заход звезды Δ, через пять месяцев. Когда же солнце, пройдя ΘΔΕ, опять окажется в точке Ε, оно произведет утренний восход звезды Δ, через тридцать дней, так как оно прошло дугу в один знак зодиака.

Теорема 2.7

У всех [неподвижных звезд], которые зодиак отделяет в северную часть [неба], утренние заходы предшествуют утренним восходам¹⁴⁴, а у всех, которые зодиак отделяет в южную часть, утренние восходы предшествуют утренним заходам.

Пусть ΑΒ является горизонтом, ΓΔ – зодиаком, Δ - некоторой звездой на восходе, а Η пусть расположена севернее [зодиака] (Рис. 21).

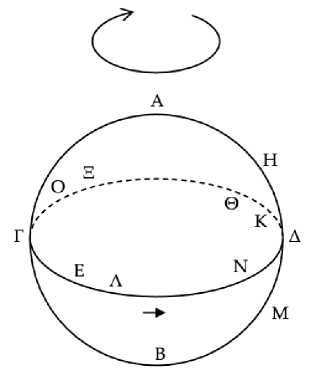
Рис. 21

Следовательно, звезда Δ восходит одновременно со звездой Η, но не заходит одновременно с ней.145 Таким образом, Η зайдет совместно с какой-то звездой из следующих146 за звездой Δ. Пусть она заходит совместно с Θ, и пусть Ε диаметрально противоположна Θ, и выберем дугу ΔΚ147 равной половине знака зодиака, и ΕΛ тоже.

И поскольку при солнце в точке Κ звезда Δ восходит утром, а Η восходит одновременно с Δ, то, следовательно, Η восходит утром при солнце в точке Κ. С другой стороны, поскольку, когда солнце находится в положении Λ, Ε восходит утром, а когда Ε восходит, Θ и Η заходят, то, следовательно, Η заходит утром при солнце в точке Λ, так как Η заходит одновременно с Θ¹⁴⁸. А при [солнце] в точке Κ она восходит утром. Таким образом, во время прохода солнцем дуги ΚΓΕΛ звезда Η переходит от восхода утром к заходу утром.¹⁴⁹ А дуга ΚΓΕΛ больше дуги ΛΔΚ, и точка Λ предшествует¹⁵⁰ точке Κ. Следовательно, от утреннего восхода [звезда] приходит к утреннему заходу за больший промежуток времени, а от утреннего захода к утреннему восходу – за меньший.¹⁵¹

Опять-таки, пусть звезда Μ будет на восходе и расположена южнее [зодиака]. И поскольку звезда Μ, восходя одновременно со звездой Δ, заходит раньше нее, то она зайдет вместе с какой-то звездой из предшествующих152 звезде Δ. Пусть она заходит вместе с Ν, и пусть Ξ диаметрально противоположна Ν, а дуга ΞΟ выбрана равной половине знака зодиака. И поскольку при солнце в точке Κ звезда Δ восходит утром, то и Μ восходит утром. С другой стороны, поскольку при солнце в точке Ο звезда Ξ восходит утром, то Ν заходит, а когда Ν заходит, то и Μ заходит. Таким образом, при солнце в точке Ο звезда Μ заходит утром. А при [солнце] в точке Κ она восходит утром. И время, за которое солнце проходит дугу ΚΟ, меньше153, а точка Κ предшествует154 точке Ο. Следовательно, от утреннего захода [звезда] приходит к утреннему восходу за больший промежуток времени, а от утреннего восхода к утреннему заходу – за меньший.155

Теорема 2.8

У всех тех [неподвижных звезд], которые зодиак отделяет на восходе в северную часть [неба], вечерние заходы предшествуют вечерним восходам156, а у всех тех, которые зодиак157 отделяет в южную часть, вечерние восходы предшествуют вечерним заходам.

Пусть ΑΒ является горизонтом, ΓΔ – зодиаком, Η – некоторая звезда на восходе, лежащая к северу [от зодиака] (Рис. 22) .

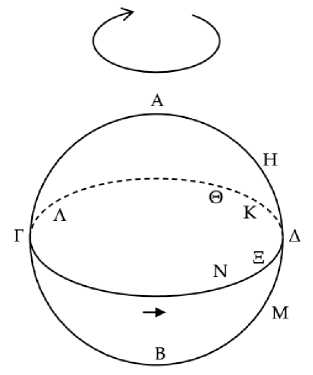
Рис. 22

Следовательно, Η восходит одновременно с Δ, но не заходит одновременно с ней.158 Таким образом, Η зайдет совместно с какой-то звездой из следующих159 за звездой Δ. Пусть она заходит совместно с Θ, и выберем дугу ΘΚ160 равной половине знака зодиака, и ΓΛ тоже. И поскольку при солнце в точке Κ звезда Θ заходит вечером, а когда Θ заходит, то и Η заходит, то, следовательно, Η заходит вечером при солнце в точке Κ. С другой стороны, поскольку, когда солнце находится в положении Λ, Γ заходит вечером, а когда Γ заходит, Η восходит вечером, то, следовательно, Η восходит вечером при солнце в точке Λ. А время, за которое солнце проходит дугу ΛΔΚ, больше времени, за которое оно проходит дугу ΚΛ. Следовательно, от вечернего восхода [звезда] приходит к вечернему заходу за больший промежуток времени, а от вечернего захода к вечернему восходу – за меньший.161

Опять-таки, пусть Μ выбрана как звезда, расположенная к югу [от зодиака]. И поскольку звезда Μ не заходит одновременно со звездой Δ, но одновременно с ней восходит, то она зайдет вместе с какой-то звездой из пред-шествующих162 звезде Δ. Пусть она заходит совместно с Ξ, и выберем дугу ΝΞ равной половине знака зодиака. Поскольку при солнце в точке Ν звезда Ξ заходит вечером, а когда Ξ заходит, то и Μ заходит, то Μ заходит вечером при солнце в точке Ν. С другой стороны, поскольку при солнце в точке Λ звезда Γ заходит вечером, а когда Γ заходит, то Δ восходит вечером, то Δ восходит вечером при солнце в точке Λ. Но Δ восходит совместно с Μ. Таким образом, при солнце в точке Λ звезда Μ восходит вечером, а при солнце в точке Ν она заходит вечером. А дуга ΛΓΝ меньше дуги ΝΔΛ. Следовательно, от вечернего захода [звезда] приходит к вечернему восходу за больший промежуток времени, а от вечернего восхода к вечернему заходу – за меньший.163

Теорема 2.9

Те из обращающихся по одному кругу звезд, которые зодиак отделяет к северу, проводят скрытыми меньшее время, чем те, которые зодиак отделяет к югу.

Пусть ΑΒΓΔ является горизонтом, ΑΒ – меридианом, а ΓΔ – зодиаком. Пусть описан параллельный круг ΗΘ, и пусть Η и Κ будут две звезды на нем: Η севернее зодиака, а Κ – южнее (Рис. 23) . Я утверждаю, что Η проводит скрытой меньшее время, чем Κ.

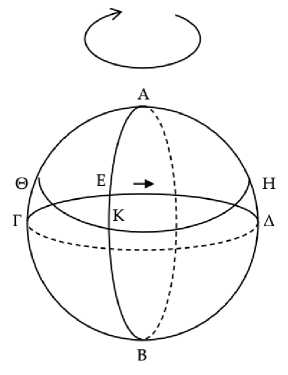
Рис. 23

Ибо поскольку Η и Ε – две звезды, причем Η расположена севернее, а Ε на зодиаке, то Η проводит скрытой меньшее время, чем Ε.¹⁶⁴ А поскольку Ε и Κ – две звезды на меридиане, причем Ε расположена севернее, а Κ – южнее, то Ε будет проводить скрытой меньшее время, чем Κ.¹⁶⁵ Но Η будет проводить скрытой меньшее время, чем Ε.¹⁶⁶ Следовательно, Η проводит скрытой меньшее время, чем Κ.

• ¹⁶⁴    Это утверждение аналогично Теореме 1.9 и может быть доказано сходным образом. Схолиаст пишет, что «это следует из Теоремы 10 в книге 1», но дошедшая до нас теорема 1.10 не об этом. Очевидно, часть теорем в первой книге утеряна (см. также прим. 166) . За теоремой 1.9 (о звездах южнее эклиптики) следовала аналогичная ей теорема о звездах севернее эклиптики (см. ее реконструированный текст в прим. 71) , и именно ее схолиаст имеет в виду.

• ¹⁶⁵    Кажется, Автолик здесь ссылается на Теорему 1.9. Так считает схолиаст.

• ¹⁶⁶    Схолия к этому месту ссылается на теорему 19 (чтение Моженэ) или 15 (чтение Хульча) из первой книги, которая в современном виде содержит лишь 13 теорем. Однако, данное утверждение Автолика – лишь повторение того, что он сказал чуть ранее в этом доказательстве, и, кажется, схолиаст мог бы вновь сослаться на теорему 1.10 (Моженэ так и исправляет). Почему он вообще решил прокомментировать это место и почему, если уж решил, не написал просто «как было показано» – загадка. В любом случае, перед нами еще одно свидетельство схолиаста, что первая книга когда-то содержала больше теорем.

Теорема 2.10

Среди звезд, отделяемых зодиаком на восходе в северную часть [неба], те, совместно заходящие с которыми [звезды на зодиаке] отстоят от совместно восходящих меньше167, чем на половину знака зодиака, переходят от утреннего восхода к вечернему восходу за пять месяцев, и в течение этого времени они наблюдаемы на восходе; от вечернего восхода к утреннему заходу за более чем тридцать дней, и в течение этого времени они пребывают скрытыми; от утреннего захода к вечернему заходу за пять месяцев, и в течение этого времени они наблюдаемы на заходе; от вечернего захода к утреннему восходу менее чем за тридцать дней, и в течение этого времени они пребывают скрытыми.

Пусть ΑΓΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда на горизонте, расположенная на восходе севернее [зодиака] (Рис. 24) .

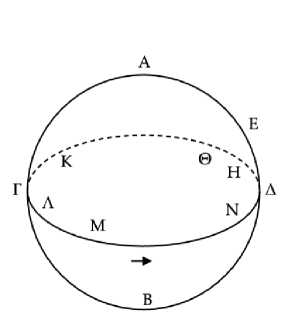
Рис. 24

Естественно, Ε восходит одновременно с Δ, но не заходит одновременно с ней. Следовательно, она заходит совместно с какой-то из следующих за Δ звезд168. Пусть она заходит совместно с Η. Итак, ΗΔ меньше половины знака зодиака.169 Выберем дугу ΔΘ равной половине знака зодиака, и ΚΓ тоже. Пусть Λ диаметрально противоположна точке Η, и выберем дугу ΛΜ рав- ной половине знака зодиака, и ΝΔΗ тоже. При солнце в точке Θ звезда Δ, а также и Ε, восходит утром. С другой стороны, при солнце в точке Κ звезда Γ заходит вечером, так как Κ заходит раньше170 Γ, а когда Γ заходит, Δ, а также и Ε, восходит. Следовательно, при солнце в точке Κ звезда Ε восходит вечером. Следовательно, звезда Ε переходит от утреннего восхода к вечернему восходу за то время, пока солнце проходит дугу ΘΚ. А дуга ΘΚ составляет пять месяцев. Далее, при солнце в точке Μ точка Λ восходит утром, так как Λ восходит раньше171 Μ, а когда Λ восходит, Η, а также и Ε, заходит. Следовательно, при солнце в точке Μ звезда Ε заходит утром. Следовательно, звезда Ε переходит от вечернего восхода к утреннему заходу за то время, пока солнце проходит дугу ΚΓΜ, а она больше знака зодиака.172 Опять-таки, при солнце в точке Ν звезда Η заходит вечером, так как Ν заходит раньше173 Η. А когда Η заходит, то и Ε заходит вечером. Следовательно, при солнце в точке Ν звезда Ε заходит вечером. Следовательно, звезда Ε переходит от утреннего захода к вечернему заходу за то время, пока солнце проходит дугу ΜΝ. А дуга ΜΝ составляет пять месяцев. А в то время, когда солнце передвигается по дуге ΝΔΘ, Ε остается скрытой. А дуга ΝΔΘ меньше знака зо-диака.174

Теорема 2.11

Все звезды, отделяемые зодиаком к югу, если совместно восходящие с ними [звезды на зодиаке] отстоят от совместно заходящих на дугу, меньшую половины знака зодиака, будут совершать вечерний восход после утреннего восхода, а затем утренний заход менее чем через тридцать дней, а затем вечерний заход, а затем утренний восход, и пребывать скрытыми в течение большего времени, чем звезды, расположенные на зодиаке.175

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Δ и Ε выбраны как две звезды на восходе, причем Ε восходит одновременно с Δ, а заходит раньше ее (Рис. 25) .

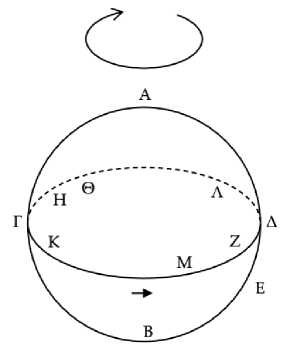
Рис. 25

Таким образом, Ε заходит вместе с какой-то из звезд, предшествующих Δ¹⁷⁶. Пусть она заходит вместе с Ζ. Итак, дуга ΖΔ меньше половины знака зодиака. Пусть Η диаметрально противоположна Ζ. Следовательно, и дуга ΓΗ меньше половины знака зодиака. Выберем дугу ΓΘ равной половине знака зодиака, и ΗΓΚ тоже, и еще ΔΛ и ΜΖ. При солнце в точке Λ звезда Δ, а также Ε, восходит утром. С другой стороны, при солнце в точке Θ звезда Γ заходит вечером, а когда Γ заходит, Δ, а также Ε, восходит вечером. Опять-таки, при солнце в точке Κ звезда Η восходит утром, а когда Η восходит, диаметрально противоположная точка Ζ заходит. А когда Ζ заходит, то и Ε заходит. Следовательно, при солнце в точке Κ звезда Ε заходит утром. А дуга ΘΗΓΚ меньше знака зодиака.¹⁷⁷ Опять-таки, при солнце в точке Μ звезда Ζ заходит вечером, а когда Ζ заходит, то и Ε заходит. Следовательно, при солнце в точке Μ звезда Ε заходит вечером. Следовательно, она переходит от вечернего захода к утреннему восходу за то время, пока солнце проходит дугу ΜΔΛ. А дуга ΜΔΛ больше знака зодиака.¹⁷⁸

Теорема 2.12

Все звезды, на восходе отделяемые зодиаком к югу, для которых совместно восходящие с ними [звезды на зодиаке] отстоят от совместно заходящих на дугу в один знак зодиака, восходят вечером и заходят утром в одну и ту же ночь, и будут пребывать скрытыми в течение большего времени, чем звезды, расположенные на зодиаке.

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – звезда на восходе, расположенная к югу [от зодиака] (Рис. 26) .

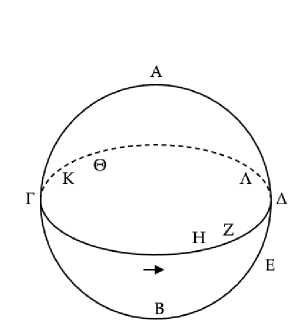
Рис. 26

Пусть Ε восходит вместе с Δ. Следовательно, она заходит вместе с некоторой звездой из предшествующих179 Δ. Пусть она заходит вместе с Ζ. Итак, дуга ΔΖ равна знаку зодиака.180 Пусть Θ диаметрально противоположна Ζ. Следовательно, и дуга ΓΘ равна знаку зодиака. И пусть дуга ΓΘ разделена пополам точкой Κ, и дуга ΖΗ равна половине знака зодиака, и ΛΔ тоже. При солнце в точке Λ звезда Δ восходит утром, и Ε тоже. А при солнце в точке Κ звезда Γ заходит вечером, так как ΓΚ равна половине [знака зодиака], а когда Γ заходит, Δ, а также Ε, восходит. Следовательно, при солнце в точке Κ звезда Ε восходит вечером. Опять-таки, при солнце в точке Κ звезда Θ восходит утром, а когда Θ восходит, Ζ заходит. А когда Ζ заходит, то и Ε заходит. Следовательно, при солнце в точке Κ звезда Ε заходит утром. Но она также и восходит вечером при солнце в точке Κ. Следовательно, в одну и ту же ночь звезда Ε восходит вечером и заходит утром. Опять-таки, при солнце в точке Η звезда Ζ заходит вечером, а когда Ζ заходит, то и Ε заходит, так что при солнце в точке Η звезда Ε заходит вечером. Но она восходит утром при солнце в точке Λ. Следовательно,181 она пребывает скрытой, пока солнце проходит дугу ΗΔΛ.182

Теорема 2.13

Если у звезд, на заходе отделяемых зодиаком к северу, совместно заходящие с ними звезды [на зодиаке] отстоят от совместно восходящих на дугу меньше половины знака зодиака, то такие звезды совершают вечерний восход после утреннего восхода, затем утренний заход, затем вечерний заход, и пребывают скрытыми в течение меньшего времени, чем звезды, расположенные на зодиаке.

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда, заходящая к северу от Γ (Рис. 27).

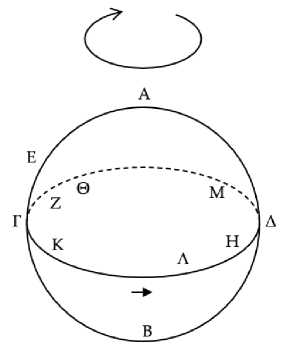
Рис. 27

Она заходит вместе с Γ, а восходит вместе с некоторой предшествую-щей¹⁸³ Γ звездой Ζ. Итак, дуга ΓΖ меньше половины знака зодиака. Пусть Η диаметрально противоположна Ζ, и выберем дуги ΘΓ, ΚΓΖ, ΛΗ, и еще ΔΜ равными половине знака зодиака. При солнце в точке Κ звезда Ζ, а также и Ε, восходит утром. С другой стороны, при солнце в точке Λ звезда Η заходит вечером, а Ζ восходит вечером, а с ней и Ε. Опять-таки, при солнце в точке Μ звезда Δ восходит утром, а когда Δ восходит, Γ заходит, а с ней и Ε. Сле-

довательно, при солнце в точке Μ звезда Ε заходит утром. Опять-таки, при солнце в точке Θ звезда Γ заходит вечером, а с ней и Ε, в то время как при солнце в точке Κ она восходит утром.184 Следовательно, Ε переходит от утреннего восхода к вечернему восходу, от вечернего восхода к утреннему заходу, а от утреннего захода к вечернему заходу, и пребывает скрытой в течение того времени, пока солнце проходит дугу ΘΓΚ, которая меньше знака зодиака. Таким образом, она проводит скрытой меньшее время, чем звезды на зодиаке.185

Теорема 2.14

Если у [звезд], на заходе отделяемых зодиаком к северу, совместно заходящие с ними [звезды на зодиаке] отстоят от совместно восходящих на дугу в один знак зодиака, то такие звезды не пребывают скрытыми, но показываются в одну и ту же ночь утром на восходе и вечером на заходе.186

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда, лежащая на заходе к северу [от зодиака] (Рис. 28) .

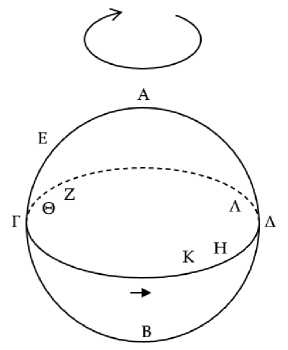
Рис. 28

Пусть она восходит вместе с Ζ, а заходит вместе с Γ. Итак, дуга ΓΖ равна знаку зодиака. Я утверждаю, что звезда Ε не будет пребывать скрытой, но в одну и ту же ночь она и восходит утром, и заходит вечером.

Ибо пусть Η диаметрально противоположна Ζ, а дуга ΓΖ разделена пополам точкой Θ. И пусть дуга ΗΚ выбрана равной половине знака зодиака, и ΔΛ тоже. При солнце в точке Θ звезда Ζ восходит утром, и следовательно, Ε восходит утром, а Γ заходит вечером, и следовательно, Ε тоже. Следовательно, в одну и ту же ночь звезда Ε и восходит утром, и заходит вечером. Опять-таки, при солнце в точке Κ звезда Η заходит вечером, а когда Η заходит, Ζ восходит, а с ней и Ε. Следовательно, при солнце в точке Κ звезда Ε восходит вечером. Опять-таки, при солнце в точке Λ звезда Δ восходит утром, а когда Δ восходит, Γ заходит, а с ней и Ε. Следовательно, при солнце в точке Λ звезда Ε заходит утром.

Теорема 2.15

Все звезды, на заходе отделяемые зодиаком к северу, если совместно заходящие с ними [звезды на зодиаке] отстоят от совместно восходящих на дугу больше знака зодиака, не пребывают скрытыми187, но в одну и ту же ночь и восходят утром, и заходят вечером188 в течение всего времени от утреннего восхода и до вечернего захода.

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда, лежащая на заходе к северу [от зодиака] (Рис. 29) .

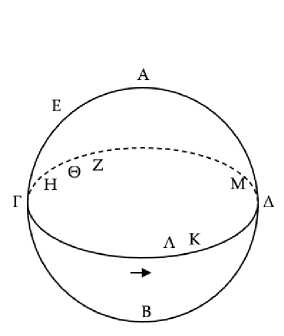
Рис. 29

Пусть она заходит вместе с Γ, а восходит вместе с Ζ, и дуга ΓΖ больше знака зодиака. Я утверждаю, что звезда Ε не будет пребывать скрытой, но что она в одну и ту же ночь и заходит вечером и восходит утром.

Ибо пусть дуга ΓΗ выбрана равной половине знака зодиака, и ΘΖ тоже. И пусть Κ диаметрально противоположна Ζ, и дуга ΚΛ выбрана равной половине знака зодиака, и ΔΜ тоже. При солнце в точке Η звезда Γ заходит вечером, а с ней и Ε. С другой стороны, при солнце в точке Θ звезда Ζ восходит утром, а с ней и Ε. Следовательно, когда солнце проходит дугу ΘΗ, звезда Ε видна и на восходе утром, и на заходе вечером. Опять-таки, при солнце в точке Λ звезда Κ заходит вечером, а Ζ восходит вечером, а следовательно, и Ε восходит вечером. С другой стороны, при солнце в точке Μ звезда Δ восходит утром, а Γ заходит утром, а следовательно, и Ε заходит утром. Следовательно, когда солнце проходит дугу ΘΓ, звезда Ε видна на восходе, а когда дугу ΜΖΗ – на заходе. Следовательно, когда солнце проходит дугу ΘΗ, звезда Ε видна и на заходе, и на восходе.

Теорема 2.16

Если у [звезд], на заходе отделяемых зодиаком к югу, совместно заходящие с ними звезды [на зодиаке] отстоят от совместно восходящих на дугу меньше знака зодиака, то такие звезды совершают вечерний восход после утреннего восхода, затем утренний заход, затем вечерний заход, и пребывают скрытыми в течение большего времени, чем звезды, расположенные на зодиаке.

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда, лежащая на заходе к югу [от зодиака] (Рис. 30) .

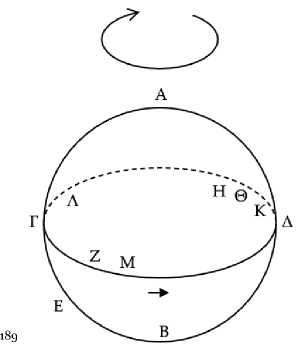
Рис. 30

Пусть она заходит вместе с Γ, а восходит вместе с некоторой из следующих за Γ звезд. Пусть она восходит вместе с Ζ, и дуга ΓΖ меньше знака зодиака. Пусть Η диаметрально противоположна Ζ, и дуга ΔΘ выбрана равной половине знака зодиака, и ΚΗ тоже, и еще ΖΜ и ΓΛ. При солнце в точке Μ звезда Ζ восходит утром, а с ней и Ε. С другой стороны, при солнце в точке Κ звезда Η заходит вечером, а Ζ и Ε восходят вечером. Опять-таки, при солнце в точке Θ звезда Δ восходит утром, а когда Δ восходит, Γ заходит, а с ней и Ε. Следовательно, при солнце в точке Θ звезда Ε заходит утром. Опять-таки, поскольку при солнце в точке Λ звезда Γ заходит вечером, а с ней и Ε, то, следовательно, в течение того времени, пока солнце проходит дугу ΛΓΜ, звезда Ε пребывает скрытой. А ΛΓΜ больше дуги одного знака зодиака. Следовательно, звезда Ε будет пребывать скрытой в течение большего времени, чем звезды, расположенные на зодиаке.

Теорема 2.17

Все звезды, на заходе отделяемые зодиаком к югу, если совместно заходящие с ними [звезды на зодиаке] отстоят от совместно восходящих на дугу в один знак зодиака, в одну и ту же ночь и восходят вечером и заходят утром, и пребывают скрытыми в течение большего¹⁹⁰ времени, чем звезды, расположенные на зодиаке.

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда, лежащая на заходе к югу [от зодиака] (Рис. 31) .

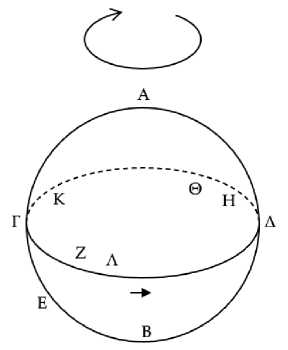
Рис. 31

Пусть она заходит вместе с Γ. Следовательно, она восходит вместе с какой-то из звезд, следующих за Γ. Пусть она восходит вместе с Ζ, и ΓΖ – дуга в один знак зодиака. И пусть Θ диаметрально противоположна Ζ, и дуга ΘΔ разделена пополам точкой Η, а дуга ΖΛ выбрана равной половине знака зодиака, и ΓΚ тоже. Поскольку при солнце в точке Η звезда Δ восходит утром, то Γ заходит утром, а с ней и Ε. С другой стороны, при солнце в точке Η звезда Θ заходит вечером, а когда Θ заходит, Ζ восходит вечером, а с ней и Ε. Следовательно, в одну и ту же ночь она и заходит утром, и восходит вечером. Опять-таки, поскольку при солнце в точке Κ звезда Γ заходит вечером, то и Ε заходит вечером. А поскольку при солнце в точке Λ восходит утром Ζ, то и Ε восходит утром. Следовательно, звезда Ε будет пребывать скрытой в течение того времени, пока солнце проходит дугу ΚΓΛ. А дуга ΚΓΛ равна двум знакам зодиака. Следовательно, Ε будет пребывать скрытой в течение большего времени, чем звезды на зодиаке.¹⁹¹

Теорема 2.18

Если у [звезд], на заходе отделяемых зодиаком к югу, совместно заходящие с ними звезды [на зодиаке] отстоят от совместно восходящих на дугу больше знака зодиака, то такие звезды имеют утренний заход после утреннего восхода, а затем вечерний восход, а затем вечерний заход, и в одну и ту это время прохождения солнцем двух знаков зодиака (для звезд на зодиаке это было бы время прохождения одного знака).

¹⁹¹ Из чего следует последнее утверждение теоремы (и даже более сильное, см. прим. 190) .

же ночь будут видимы и на восходе, и на заходе в течение времени от утреннего захода до вечернего восхода, а скрытыми будут пребывать в течение большего¹⁹² времени, чем звезды, расположенные на зодиаке.

Пусть ΑΒ является горизонтом, а ΓΔ – зодиаком. И пусть Ε – некоторая звезда, лежащая на заходе к югу [от зодиака] (Рис. 32) .

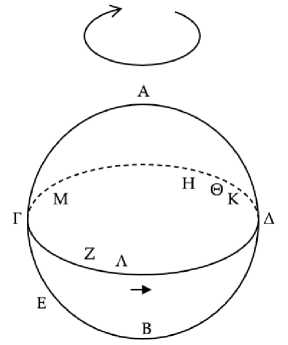
Рис. 32

Пусть она заходит вместе с Γ, а восходит вместе с Ζ, и пусть дуга ΓΖ больше знака зодиака. И пусть Η диаметрально противоположна Ζ, а дуга ΗΘ выбрана равной половине знака зодиака, и ΚΔ тоже, и еще ΖΛ и ΓΜ. При солнце в точке Λ звезда Ζ восходит утром, а с ней и Ε. С другой стороны, при солнце в точке Κ звезда Δ восходит утром, а диаметрально противоположная Γ заходит утром. Следовательно, и Ε заходит утром. Опять-таки, при солнце в точке Θ звезда Η заходит вечером, а когда Η заходит, Ζ восходит вечером, а следовательно, и Ε восходит вечером. Следовательно, когда солнце проходит дугу ΚΘ, звезда Ε в одну и ту же ночь и восходит, и заходит. Опять-таки, при солнце в точке Μ звезда Γ заходит вечером, а с ней и Ε. А при солнце в точке Λ она восходит утром. Следовательно, звезда Ε будет пребывать скрытой все время, пока солнце проходит дугу ΜΓΛ. А дуга эта больше двух знаков зодиака.¹⁹³