Автоматическая генерация графов для электронных обучающих систем

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 519.1                                           

В связи с пандемией коронавируса возросла потребность в автоматизированных системах обучения, так как они позволяют расширить возможности дистанционного образования. Одними из их достоинств являются: осуществление удаленного доступа, самостоятельное изучения материала студентами, а также упрощение процесса проверки знаний преподавателем. Однако информационная сфера требует постоянного развития, поэтому обучающие системы необходимо совершенствовать, добавляя в них новые возможности и повышая уровень комфорта использования, стараясь при этом использовать ресурсы как можно более оптимально. В этой работе рассматривается один из важных аспектов разрабатываемой обучающей системы решения некоторых задач теории графов, а именно: генерация графов. Автоматизированные системы обучения, нацеленные на решение задач, связанных с графами, не являются новшеством в современном мире. Нередко в таких системах задания выбираются из некоторого ограниченного набора, хранящегося в банке задач. Данный подход имеет ряд недостатков [1–2].

• 1.    Большое количество задач нагружает базу данных системы, что приводит к долгому выполнению приложения.

• 2.    Для поддержания актуальности банка заданий преподавателю необходимо постоянно его обновлять.

• 3.    При малом объеме банка задач велика вероятность повторения заданий, что приводит к неточным результатам тестирования знаний студентов.

По сравнению с методом банка задач метод генерации графов имеет следующие преимущества:

• 1.    Большее количество вариантов задач.

• 2.    Снижение нагрузки с преподавателей, так как генерацией графов занимается сама система.

• 3.    Снижения нагрузки на базу данных, так как задания генерируются непосредственно перед решением, а не хранятся в системе заранее.

Тем не менее существует ряд особенностей, которые необходимо учитывать при генерации графов. В рамках разрабатываемой обучающей системы первоначально реализуется отработка решения задач раскраски графов. Чаще всего при этом используются неориентированные связные графы без петель и кратных ребер, иными словами — простые связные графы. Поэтому рассмотрим генерацию графов именно такого вида. При составлении и решении задач на вычислительных машинах графы представляют дискретным способом. Таких способов существует большое количество и от выбора способа сильно зависит эффективность алгоритма генерации графов. Среди дискретных представлений графов наиболее популярными и используемыми являются матричные. В виде матрицы смежности, либо матрицы инцидентности. Кроме того, существует не матричные способы представления, но не менее удобные в некоторых случаях. Одним из таких, являются списки смежности. В этом способе граф представляется с помощью списочной структуры, которая определяет смежность вершин и состоит из массива указателей на списки смежных вершин. Такой способ представления в общем случае отличается более оптимальным использованием памяти. Для неориентированных графов, содержащих p вершин и q ребер, объем используемой памяти составляет О(p+2q) [1, c. 244].

Также стоит вопрос: как можно распределить генерируемые задачи по сложности? Наиболее простой способ — распределение по количеству вершин. Такой способ, возможно, не даст высокий уровень точности, но и не нагрузит систему. Будем генерировать графы трех уровней сложности:

• 1.    простые — от 5 до 7 вершин;

• 2.    средние — от 8 до 10;

• 3.    сложные — от 11 до 13.

Необходимо учитывать, что генерируемый граф должен быть связным. Для обеспечения этого условия будем придерживаться следующего алгоритма.

• 1.    Генерируются случайные непустые списки смежности графа с заданным числом вершин.

• 2.    Выполняется проверка на связность графа. В том случае, если граф не связен, осуществляется переход к пункту 1.

Осталось определиться со способом проверки графа на связность. Существует теорема, что если граф связен и конечен, то поиск в ширину и поиск в глубину обойдут все вершины по одному разу [1, c. 246].

Также одно из следствий этой теоремы утверждает, что поиск в ширину в среднем вдвое медленнее, чем поиск в глубину [1, c. 247].

Таким образом, для проверки связности графа будем использовать метод поиска в глубину. В процессе обхода графа будем помечать вершины, которые уже были рассмотрены. Если по завершении обхода не останется ни одной не помеченной вершины, граф является связным. Удобным представлением графов при реализации алгоритмов обхода графов являются списки смежности. С учетом требований к генерируемым графам, отмеченным выше, был написан программный код на языке С# для решения поставленной задачи.

Для представления графа был создан класс Graph (Рисунок 1). В переменной Vertex будем хранить вершину графа, а в VertexList — список смежных ей вершин.

public class Graph public int Vertex { get; set; } public List VertexList { get; set; } }                                                                             '                            '

Рисунок 1. Класс Graph

Следующая часть кода отвечает за генерацию случайного графа (Рисунок 2). Список смежности графа будем хранить в списке graph. Для каждой из вершин (количество вершин в данном примере задано фиксированно для удобства тестирования и демонстрации) генерируем случайный непустой список смежных вершин. Здесь же проверяем, чтобы в списке не было вершины, для которой он составляется, т. е. избегаем петель. После того, как граф сгенерирован, остается проверить его на связность. Реализация алгоритма обхода в глубину продемонстрирована на Рисунках 3–4.

Бюллетень науки и практики / Bulletin of Science and Practice Т. 7. №6. 2021

Random rnd = new Random();

int p;

p = 16;

bool connected = false;

List graph - new List (p); while (!connected) { for (int i = 1; i <= p; i++)

List vertexList = new List();

}                   ’                   ’

}

Рисунок 2. Генерация графа bool[] check = new bool[p+l];

check[0] = true;

DFS(graph, 1, check);

if (!check.Contains(false)) connected = true;

Рисунок 3. Проверка графа на связность static public void DFS (List graph, int start, bool[] check) { check[start] = true;

foreach (var u in graph[start-l].VertexList)

{                                                    ’                 ’ if (!check[u]) {

DFS(graph, u, check);

} }

Рисунок 4. Функция DFS – Обход графа в глубину

Функция DFS — рекурсивная функция, реализующая алгоритм обхода графа в глубину. В случае, если граф не связный, программа генерирует новый граф и проверяет на связность уже его. Результат работы программы продемонстрирован на Рисунке 5a — это составленный список смежности графа, удовлетворяющего поставленным требованиям. Для наглядности приведена также диаграмма этого графа на Рисунке 5б.

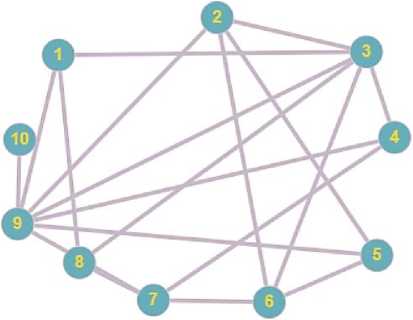
б) диаграмма

• а) список смежности

Рисунок 5. Сгенерированный граф