Автоматический синтез цифровых схем по их функциональному описанию

Под функциональным описанием схемы понимается описание логики ее работы. Такое описание может быть выполнено в виде функциональной схемы устройства, функциональных диаграмм, а также в виде функциональных выражений. Для получения функциональных выражений, описывающих логику работы цифровых схем и их элементов, предлагается использовать математический аппарат теории λ-исчисления [1].

В связи с тем, что в теории λ-исчисления функции рассматриваются с математической точки зрения как отношение входных параметров к выходным [2], то проводя аналогию с цифровыми схемами, которые также можно представить в виде отношения входных сигналов к выходным, следует вывод, что функциональные выражения, составленные по правилам λ-абстракции, удобно использовать для описания логики работы цифровых схем.

• 1.    Правила, определяющие порядок разбора функциональных описаний цифровых схем

• 2.    Алгоритм синтеза схемы по ее функциональному описанию

Функциональные выражения есть не что иное, как λ-термы. При помощи λ-термов можно описывать и один простой объект, и сложную структуру объектов, в которой согласно теории λ-исчисления сами функции могут использоваться как аргументы для функций высшего порядка [2]. Т.е., описание схемы строится из основных базовых элементов, которые составляют в более сложные структуры. Кроме этого, количество λ-выражений, используемых для описания одной схемы, зависит от количества выходов (выходных функций) схемы. Каждому выходному сигналу соответствует свой λ-терм.

Для автоматизации синтеза структуры схемы и взаимосвязи элементов схемы на основе ее функционального описания применяются правила конверсии и редукции λ-термов, описывающих схему. В результате свертки пошагово выявляется структура схемы, а также связи между элементами, что и позволяет произвести синтез цифровой схемы по ее функциональному описанию.

Анализ λ-термов нужно проводить, ориентируясь на скобочную запись, и, выполняя поэтапную свертку λ-выражения, привести его к элементарному объекту. Далее в ходе сопоставления с λ-описанием логических констант и базовых логических элементов выделяются и отображаются отождествленные элементы схемы. Затем разбор продолжается, при этом могут анализироваться временно введенные выражения, использованные при выполнении свертки. Построение схемы будет производиться справа-налево, т.е. от выходной функции к аргументам-входным переменным.

На основе правил разбора функциональных выражений, рассмотрим по шагам, как будет происходить синтез сложной цифровой схемы, представленной 4-х разрядным параллельным регистром памяти, построенным на RS-триггерах с общими цепями управления (рис.1).

В основе схемы лежит описание RS-триггера, на вход S подается результат конъюнкции управляющего сигнала записи «Зп» и информационного « DIi ». Информация хранится до тех пор, пока не поступит сигнал чтения «Чт». После прихода сигнала «Чт» информацию можно считывать с выхода «Qi ».

Сигналы обозначим удобными для описания символами Уст«0»=r, DI_i = d_i , Зп=Z, Чт=C, q_i =сигнал обратной связи триггера.

Схема имеет 4 выхода « Q 1 », « Q₂», « Q₃», « Q₄ », а, значит, для полного ее описания строится 4 Х-выражения:

Q i = I d i Zq i rC .((( d i ( Z 1 ) 1 ) 1 )((( q 1 (( r 1 ) 1 ) 1 ) 1 ) 1 ) 1 )( C 1 ) 1 (1) Q 2 = X d 2 Zq 2 rC . ((( d 2 ( Z 1 ) 1 ) 1 )((( q 2 (( r 1 ) 1 ) 1 ) 1 ) 1 ) 1 )( C 1 ) 1 (2) Q 3 = X d 3 Zq 3 rC . ((( d 3 ( Z 1 ) 1 ) 1 )((( q 3 (( r 1 ) 1 ) 1 ) 1 ) 1 ) 1 )( C 1 ) 1 (3) Q 4 = X d 4 Zq 4 rC . ((( d 4 ( Z 1 ) 1 ) 1 )((( q 4 (( r 1 ) 1 ) 1 ) 1 ) 1 ) 1 )( C 1 ) 1 (4)

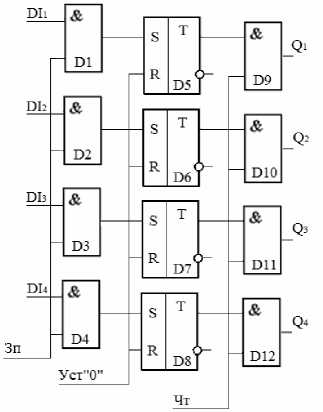
Рис.1. Схема 4-х разрядного параллельного регистра памяти

Из анализа выражений Х-термов видно, что входными для схемы являются сигналы «г», « d i », «Z», «С». Для выполнения синтеза производится разбор каждого выражения по шагам на основе правил, определенных в разделе 1 статьи.

Шаг 1. Разбираем первый Х-терм, описывающий схему формула (1). Анализируя структуру выражения, в нем можно выделить три части: две части это выражения в скобках ((( d 1 ( Z 1 ) 1 ) 1 )((( q 1 (( r 1 ) 1 ) 1 ) 1 ) 1 ) 1 ) и ( C 1 ), третья часть представлена константой 1 .

Наиболее сложное представление имеет выражение в первой скобке, оно представляет собой сложную функцию, которую для удобства можно обозначить произвольным символом и продолжить ее анализ позднее. Выражение во второй скобке состоит из переменной, обозначающей входной сигнал и константы и в преобразованиях не нуждается.

Шаг 2. Пусть функция f (d 1, Z, q1, r) = Xd 1 Zq1 r.((d 1( Z 1) 1) 1)((( q 1(( r 1) 1) 1) 1) 1) 1 (5) обозначается символом « x 1», тогда Х-терм выходной функции в результате конверсии примет вид

Q 1 ( x 1 , C ) = X x 1 C . x 1 ( C 1 ) 1 . (6)

Выражение полученного λ-терма совпадает с описанием логического элемента «И», на вход которого подаются сигналы « x ₁ » и «C», причем на « x ₁ » приходит сигнал с выхода схемы, описанной функцией f ( d ₁ , Z , q ₁ , r ) . На этом основании можно сделать вывод о том, что описанный элемент является конъюнктором с двумя входными сигналами « x ₁ » и «C» и одним выходным Q ₁ (рис. 2).

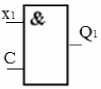
рис. 2

Таким образом, произведен синтез первого элемента схемы, который соответствует элементу D9.

Шаг 3. Рассматриваем функцию, определенную в формуле (5), которая на предыдущем шаге обозначалась « x ₁ ». Выражение λ-терма состоит из трех частей, две из которых также описываются сложными выражениями ( d ₁ ( Z ⊥ ) ⊥ ) и ((( q ₁ (( r ⊥ ) ⊥ ) ⊥ ) ⊥ ) ⊥ ) . Поэтому продолжаем свертку.

Шаг 4. Пусть s1 =λd1Z.d1(Z⊥)⊥.(7)

В результате конверсии для x1 получаем функцию от трех переменных x1 = f(s1,q1,r) = λs1q1r.(s1(((q1(r ⊥) ⊥) ⊥) ⊥) ⊥) ⊥.(8)

Полученный λ-терм имеет сложную структуру и состоит из двух частей. Первая – это выражение в скобках, вторая – константа ┴ . Если выражение в скобках определить функцией:

f(s1,q1,r) = λs1q1r.s1(((q1(r ⊥) ⊥) ⊥) ⊥) ⊥ и обозначить y1 , то в результате конверсии f(y1)=λy1.y1 ⊥, что совпадает с описанием логического элемента «НЕ». Выход схемы будет подан на вход x1 предыдущего элемента схемы. Для удобства синтезированный элемент обозначим D51(рис.3).

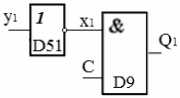
рис. 3

Шаг 5. Производится разбор выражения (9). Этот λ-терм имеет сложную структуру, не сопоставляется ни с одним базовым элементом. Переменные « s ₁ » и «r» поступают на вход анализируемой схемы, а на выходе будет формироваться сигнал y ₁ .

Проанализировав выражение терма, видно, что оно состоит из трех частей: первая часть – это переменная «s1», вторая часть – сложное выра- жение, и третья – константа. По структуре близко к описанию логического элемента «И», но все еще требуется проведение свертки.

Шаг 6. Рассмотрим вторую часть выражения y ₁ . Пусть

f ( q ₁, r ) = λ q ₁ r .( q ₁( r ⊥ ) ⊥ ) ⊥                     (10)

и обозначается n1 , тогда y1 = λs1n1.s1(n1 ⊥) ⊥ .                         (11)

Теперь описание y ₁ совпадает с описанием логического элемента «И», на вход которого приходят сигналы s ₁ и n ₁ , а на выходе получается y ₁ , обозначим его D52 (рис. 4).

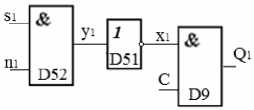
рис. 4

Шаг 7. Элементы «И» (D52) и «НЕ» (D51) соединены последовательно, причем элемент D51 лишь инвертирует выходной сигнал y ₁ с элемента D52, поэтому графически их можно объединить в один элемент «И-НЕ» (D53), для которого s ₁ и n ₁ - входные сигналы, x ₁ - выходной (рис.5).

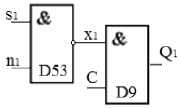
рис. 5

Шаг 8. Производится разбор функции (10), обозначенной на шаге 6 как n 1 . Выражение λ-терма этой функции состоит из двух частей: выражения в скобках и константы ┴ .

Пусть m1 = Xq 1 r. q1( r 1) 1,                         (12)

тогда f ( m ₁) = λ m ₁. m ₁ ⊥ . Она совпадает с описанием логического элемента «НЕ», обозначим его D54. Для элемента D54 m ₁ входной сигнал, а n ₁ – выходной, который поступает на вход элемента D53 (риc. 6).

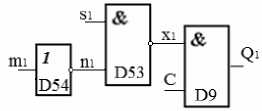
рис. 6

Шаг 9. Анализируя выражение (12), видно, что оно совпадает с описанием логического элемента «И» и имеет 2 входных сигнала « q ₁ » и «r» и один выходной « m ₁ » (D55) (рис. 7).

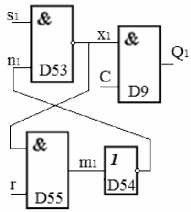
рис. 7

Шаг 10. Элементы «И» (D55) и «НЕ» (D54) соединены последовательно, причем D54 лишь инвертирует выходной сигнал с элемента D55, поэтому их можно объединить в один элемент «И-НЕ» (D56) (рис. 8).

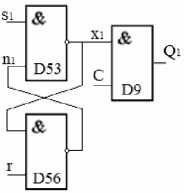
рис. 8

Шаг 11. Элементы D53 и D56 представляют собой схему RS-триггера, их можно изобразить при помощи условно-графического изображением триггера (рис. 9).

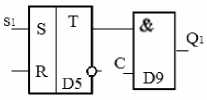
рис. 9

Шаг 12. Последнее выражение, оставшееся без анализа (7). Его описание совпадает с описанием логического элемента «И», на который поступает два входных сигнала «d1» и «Z», выходной «s1», являющийся входом для RS-триггера (рис. 10).

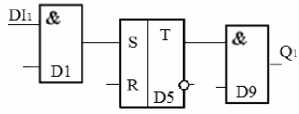
рис. 10

Таким образом, за 12 шагов проанализирован и разобран первый λ-терм, описывающий 4-х разрядный регистр. Остальные λ-термы разбираются аналогично согласно указанного алгоритма. В результате выполнения всех шагов алгоритма произведен синтез принципиальной схемы цифрового устройства.

Заключение

На основе проведенной работы можно сделать вывод о том, что функциональное описание цифровых схем с использованием математического аппарата λ-исчисления наиболее удобно для проведения синтеза структуры цифровых схем и предполагает возможность автоматизации процесса синтеза. А в дальнейшем автоматизация синтеза структуры схемы и определения взаимосвязей между ее элементами согласно предложенного алгоритма может стать основой для автоматического построения принципиальной схемы устройства.