Автоматическое управление беспилотными транспортными средствами

Беспилотные транспортные средства (БТС) все чаще применяются как для грузовых и пассажирских перевозок, так и для военных целей. Особую актуальность проблема автоматического управления приобретает для грузового и пассажирского городского электротранспорта.

Один из аспектов проблемы управления БТС связан с необходимостью организации самостоятельного движения по заданной траектории, ориентируясь на реперные точки (маячки) и сигналы локальных или глобальных навигационных систем. Другой аспект предполагает движение с заданной скоростью на различных интервалах траектории. При этом нужно отслеживать противодействие среды:

пересеченность местности, течения, ветер, состояние покрытия дорог, случайный характер загрузки.

Целью статьи является построение математических моделей транспортных средств различного вида и развитие методов автоматического управления их движением. Управление должно давать возможность перемещения по заданной траектории в условиях меняющейся обстановки и противодействия окружающей среды.

Метод задания уравнения траектории полиномиальной функцией

Рассмотрим построение траектории движения в виде графика гладкой функции локальных земных координат х, у : у = f ( x ), рисунок 1. Этот график должен проходить через заданные точки ( x ₀, у ₀), ( x 1 , у 1 ) , .. , ( x n , y n ) или в непосредственной близости от них. Выберем функцию f (x ) для определенности в виде полинома четвертой степени и положим n = 4 у = f ( x ) = а о + a 1 x + a ₂ x ² + a ^ x ³ + a ₄ x ⁴.               (1)

Коэффициенты полинома необходимо определить.

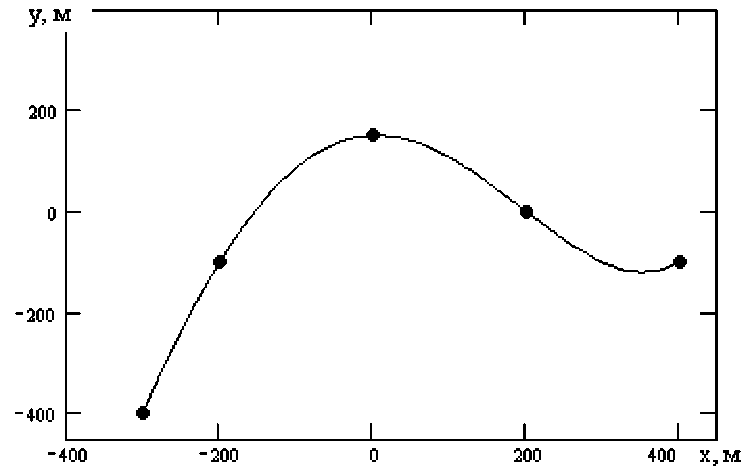
Рисунок 1 - Траектория движения

Наиболее простой способ состоит в подстановке координат точек в

(1) и решения полученной системы уравнений для коэффициентов а0, аъ... а4:

у о = а о + a 1 x о + a 2 x о + a 3 x 0 + a 4 x 0 ;

234 y 1 — a 0 + a 1 x 1 + a 2 x 1 + a 3 x 1 + a 4 x 1 ;

>

.

у 4 — a 0 + a 1 x 4 + a 2 x 4 + a 3 x 4 + a 4 x 4

Выбирая, например, точки с координатами (-300, - 400); (-200, -100);

( 0, 150); ( 200, 0); (400, - 100), получаем коэффициенты: а ₀ = 150;

а 1 — 0,051; а 2 — -5,44^10 " ³ ; а ₃ = 4,97 4 0 " ⁶ ; а ₄ = 1,0Н0 "8 .

Однако система (2) не всегда поддается решению. Это связано с тем, что при сложном виде траектории формула (1) не дает графика, проходящего через заданные точки ни при каких значениях коэффициентов. Тогда коэффициенты определяем методом наименьших квадратов [1].

Для этого составим суммарное квадратичное отклонение функции (1) от заданных точек

£ = Е ( y i — ( a 0 + a 1 x i + a ₂ x ² + a 3 x 3 + a ₄ x ⁴))² .              (3)

i — 0

Коэффициенты a i , i = 0,1...4 нужно выбрать так, чтобы отклонение (3)

стало минимальным. Согласно условию минимума подсчитаем производную от отклонения £ по коэффициентам ai, i — 0,1...4 и приравняем к нулю. Получим систему пяти уравнений с пятью определяемыми коэффициентами

А 00 а 0 ⁺ А 01 ^а 1 ⁺ А 02 а 2

⁺ А 03 а 3 ⁺ А 04 а 4 = В 0^;

А 10 а 0 + Ац а 1 + А 12 а 2 + А 13 а 3 + А 14 а 4 — В 1 ;

.

А 40 а 0 + А 41 а 1 + А 42 а 2 + А 43 а 3 + А 44 а 4 — В

Обеспечение движения по траектории

Рассмотрим движение БТС массой т по поверхности в земных координатах х, у со скоростью V под действием силы F , рисунок 3. Разложим силу и скорость на составляющие по осям х, у . Тогда составляющая силы F x будет обеспечивать составляющую скорости V x и перемещение вдоль оси x . Аналогично - F y обеспечивает составляющую скорости V y и перемещение вдоль оси у .

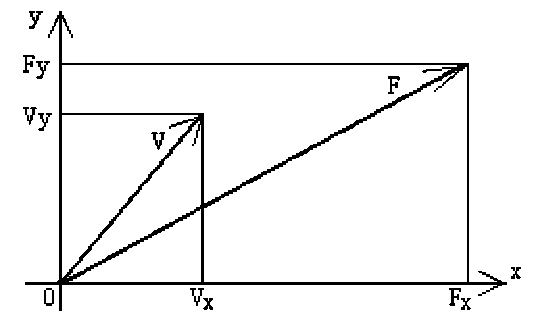
Рисунок 3 - Составляющие силы и скорости движения

По определению скорости

dx = V ■ dt ^x

dy dt Vy ’

У = V ² + у²

V V x X ^{+ V} у .

Ускорения вдоль осей подчиняются второму закону Ньютона dV m—- = Fx ;

dt x

dV

y dt     y

Кроме движущей силы, на БТС действует сила сопротивления, составляющие которой будем для определенности полагать пропорциональными скорости Fcx = kXVX; Fcy = kyVy, где kx, ky -коэффициенты пропорциональности.

Объединяя, получаем наиболее общие, упрощенные уравнения движения БТС:

dx = v ■ dt x dV F - kxVx x   x   xx dt      m

dy dt Vy ■ dV F -к V y   y   yy dt      m

Изменяя составляющие силы Fx и Fy , получаем возможность управлять составляющими скорости Vx и Vy , т.е. управлять направлением и скоростью движения БТС.

Поставим задачу управления, обеспечивающего движение БТС по заданной траектории (1), рисунок 1. Для этого при каждом значении координаты х будем контролировать отклонение реального положения БТС (координата у ) от соответствующей точки на заданной траектории

f ( x ) : A _y = f ( x ) - y . Будем корректировать составляющую силы F_y так, чтобы отклонение A _y уменьшалось. В случае, когда реальное положение у выше траектории, нужно так изменить F_y , чтобы V_y стала отрицательной, и у , уменьшаясь, приблизилось бы к f ( x ) и наоборот.

В соответствии с этими соображениями система уравнений (8)

примет вид dx = V ■ dt x dVy _Fy + (f (x) - y) ктр - kyVy dt             m где kTp– коэффициент, подбираемый из условия близости положения БТС к заданной траектории.

На рисунке 4 (а) изображена заданная траектория по (1) и траектория реального движения, рассчитанная решением уравнений (9). Эти уравнения решались в среде MathCad с учетом значений параметров БТС: m = 1000 кг; k x = 1500; k y = 1500; F x = 8000H. Начальные значения координат БТС при t = 0: x (0) = - 300; y (0) = - 400; начальные значения скоростей - нулевые: V_x (0) = V_y (0) = 0. После численного эксперимента оказалось, что заданная и реальная траектории достаточно близки при k_Tp = 1000.

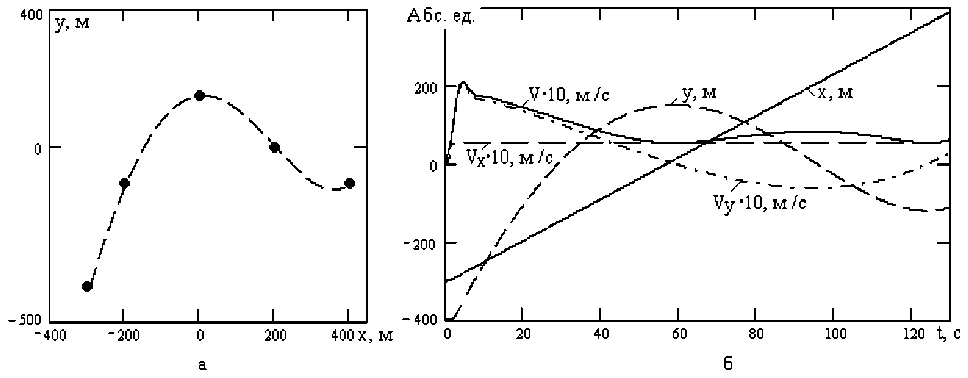
Рисунок 4 – Движение по заданной траектории

На рисунке 4,б изображены графики составляющих скоростей и общая величина скорости V , соответствующие движению по рисунку 5,4. Графики показывают, что скорость движения не остается постоянной, а испытывает значительные изменения, особенно в поворотных точках траектории, где V y = 0. Поэтому далее ставится задача стабилизации скорости.

Стабилизация скорости

Поставим задачу поддержания величины общей скорости движения на желаемом уровне. Для этого в каждый момент времени движения будем контролировать отклонение фактической величины общей скорости от заданного значения V_o(t ) : a_v = v 2 ( t ) - ( v - + v 2 ) . Регулировку скорости будем осуществлять за счет составляющей силы F , увеличивая ее при V - (t ) - ( V² + V_y " ) >  0 и наоборот. В соответствии с этим, уравнения (9)

примут вид dx ht " x ’ dvx _Fx + (V2 (t) - (Vx2 + vy))kv - kxVx dt                m

dy dt V;

dV y _F y + ( f (x) - y ) k Tp - k y V y dt             m

На рисунке 5,а изображено движение БТС по заданной траектории, а на рисунке 5,б - соответствующие графики скорости при желаемом значении Vo(t) = 15 м/с. Значение коэффициента kv экспериментальным путем подобрано kv = 115. Рисунки 5 показывают, что по сравнению с нерегулируемой скоростью на рисунке 4 колебания скорости уменьшились, и ее значение приближается к заданной величине.

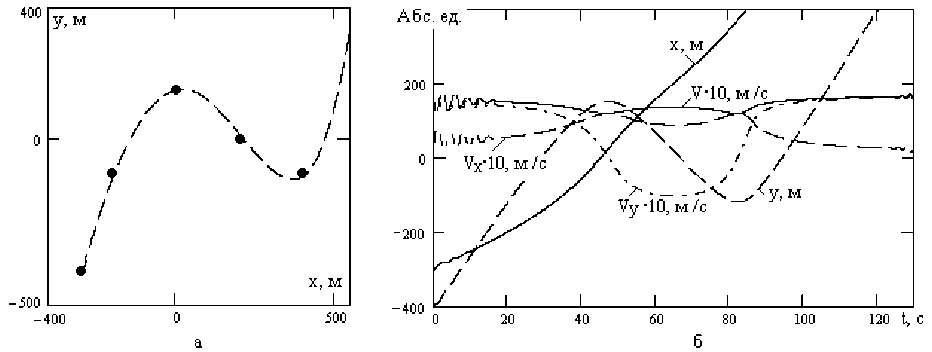
Рисунок 5 - Стабилизация скорости движения

Учет влияния противодействия среды

Рассмотрим движение БТС по пересеченной, холмистой поверхности. Рельеф поверхности нужно задать функцией двух переменных H ( x , у ). В качестве модельной выбрана функция

Химмельблау [2]

H(x , у) = 140 - ( (0,01 x )² + 0,01 у - 11 ) 2 - ( 0,01 x + (0,01 у )² - 7 ) 2 .          (11)

Ее график изображен на рисунке 6,а, а линии уровня – на рисунке 6 (б).

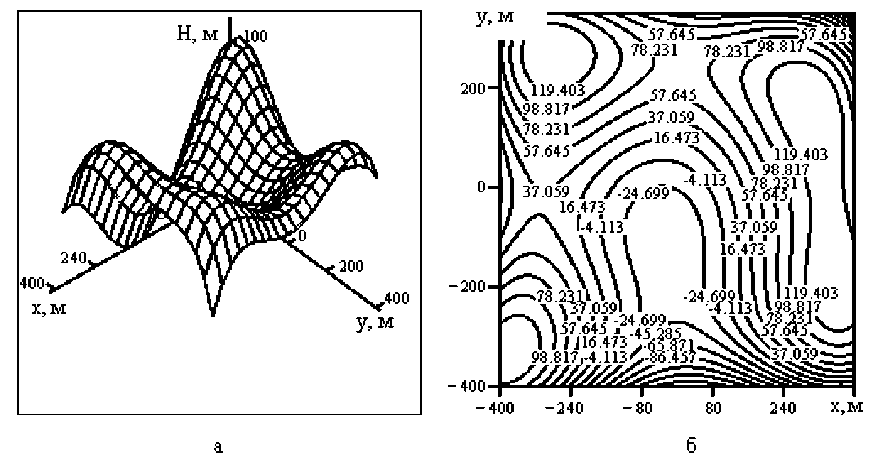
Рисунок 6 – Холмистая поверхность

При движении БТС «на горку» возникает дополнительная сила сопротивления Fc = mg • sin у, рисунок 7,а.

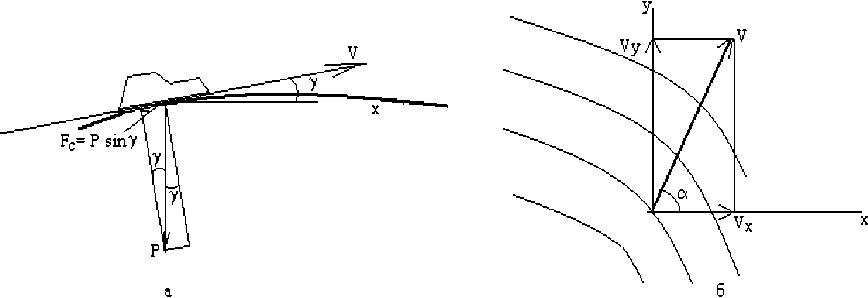
Рисунок 7 – Силы и скорости движения по холмистой поверхности

Пусть скорость движения по направлению l характеризуется углом

V         Vy a по отношению оси абсцисс, рисунок 7,б: cosa = ^x; sin a =

V

.

Тогда тангенс угла наклона дорого в направлении

l определяется

dH dH     dH .

производной по направлению tg Y=   =    _{cos a+}    sin _a .

dl   dx        dy

dl

Выражая sin у

через tgY , получаем sin y =

tg Y

dH dl

A A ^{+ (} tg ^{Y )2}    1 ₊ ( dH )²

dl

. Тогда составляющие

тормозящей силы вдоль координатных осей примут вид

Fcx = mg •

( dH

V

—cos a + dx

dH .  )

---sin a

dy

Y

• cos a ;

^F c у = mg •

dH

dH

---cos a+-- sin a • sin a

V dx        dy     Y

.

Эти силы влияют на движение БТС и учитываются в уравнениях (10)

dx dTt ” x;

dVx _F)C + V (t) - (Vx + Vy )) kv - kxVx - Fcx dt dy dt y;

dV y _F y + ( f ( x ) - У ) к тр

m

—

k y V y

—

F cy

;

dt

m

При движении «под горку» силы F_cx , F_c у способствуют увеличению скорости. На рисунке 8,а изображена траектория движения (1) на холмистой местности по (11). На рисунке 8,б – соответствующие графики скоростей и силы сопротивления F_c . Не смотря на влияние силы сопротивления, за счет средств стабилизации общая скорость V удерживается вблизи желаемого уровня.

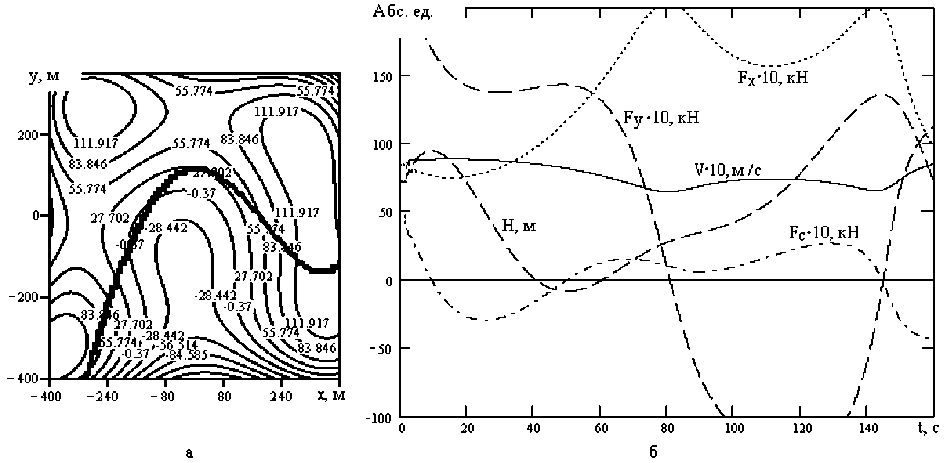
Рисунок 8 – Движение по холмистой поверхности

Таким образом, упрощенное математическое описание автоматического управления движением в общем виде построено.

Ближайшей задачей является построение управления движением конкретных, реальных БТС.

Объезд препятствий

Идея использования отталкивающих и притягивающих множеств в системах уравнений подвижными объектами предложена в работе [1], в которой представлен метод потенциалов в задаче выбора пути беспилотного транспортного средства. Идея основана на преобразовании точечных препятствий в репеллеры (от англ. repellent – отталкивающий, отвращающий). Такой подход позволяет реализовать движение в средах с препятствиями без картографирования. Этот подход может применяться и в трехмерном пространстве, а также в среде с препятствиями, имеющими различные формы. Идея представления препятствий репеллерами также может применяться при решении задач путевого уравнения.

Рассмотрим беспилотное транспортное средство, описываемое уравнениями:

dt d,Vx

= fx

Как было получено ранее, для поддержания движения БТС по заданной траектории у = ^to и с заданной скоростью V0 силы fx и fy должны определяться из выражений (номера предыдущих формул для fx и fy ).

Определим координаты препятствия x_p y_p .

Буквой r обозначено расстояние между препятствием и текущим положением БТС.

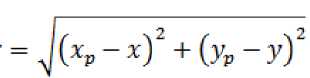
Будем полагать, что со стороны препятствия на БТС действует отталкивающая сила F , обратно пропорциональная расстоянию и направленная по прямой от точки P к точке БТС . Разложим эту силу по координатным осям x и y : F_x = — F cosa и F_y = — F sina . Из подобия

Хр—х .      уп—у треугольников следует, что с^-т = —— ; s;^:7 = ——. Определив силу

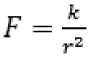
, получаем дополнительные силы по осям

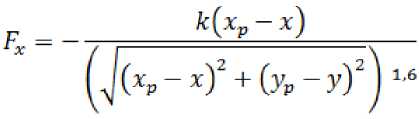
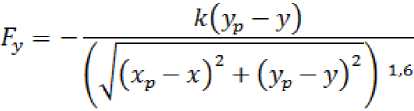
Эти силы прибавляются к силам ;’. и f. в уравнениях (1).

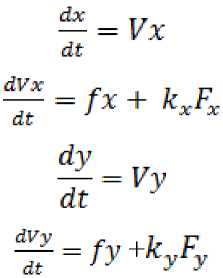
Н (2)

Коэффициент k в формулах F x и F y выбран k=150 из соображений, что на расстоянии несколько метров до препятствия сила уже давала ощутимый эффект. Коэффициенты K x , K y в формулах (2) характеризуют удельный вес силы репеллера по осям. При пологой траектории (малый угол а ) следует брать K y > K x ; при крутой траектории (большой угол а ) должен быть K x > K y для успешного объезда.

Так как силы f_x и f_y стремятся удерживать БТС на заданной траектории, то при приближении к препятствию эти силы следует ослаблять, чтобы они не мешали объезду. С этой целью в выражениях сил f x и f y вводятся ослабляющие коэффициенты K V и K_mp :

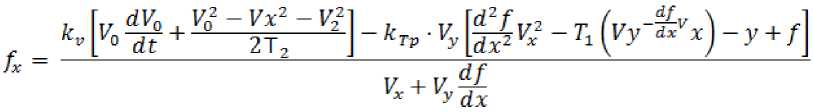
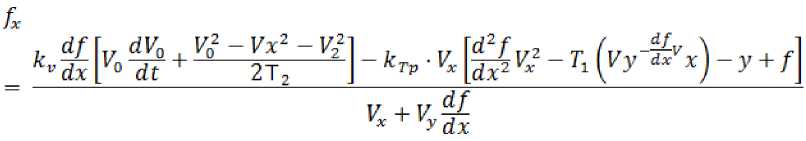
Благодаря этой коррекции БТС снижает скорость по мере приближения к препятствию, объезжает его и затем снова увеличивает скорость.

Отметим, что объезд препятствия можно было организовать путем установки нескольких новых опорных точек на траектории. Тогда необходимости в репеллере бы не было, однако это сильно исказило бы траекторию, и точность ее отслеживания снизилась бы. Увеличенное число опорных точек усложнило бы вид функции У = <рМ . Введение репеллера требует только задания координат точки препятствия. Вдали от препятствия сила репеллера не действует, и траектория не искажается. Происходит локальное искривление траектории и ослабление скорости.

На рисунках 9 (а, б) приведена траектория движения БТС по заданной ранее траектории с координатами препятствия у р =45 м; х р =125,4 м; . Коэффициенты репеллера выбраны следующими: К_x = 0,2; К_y = 0,65; К v = 0,8; К тр = 0,5.

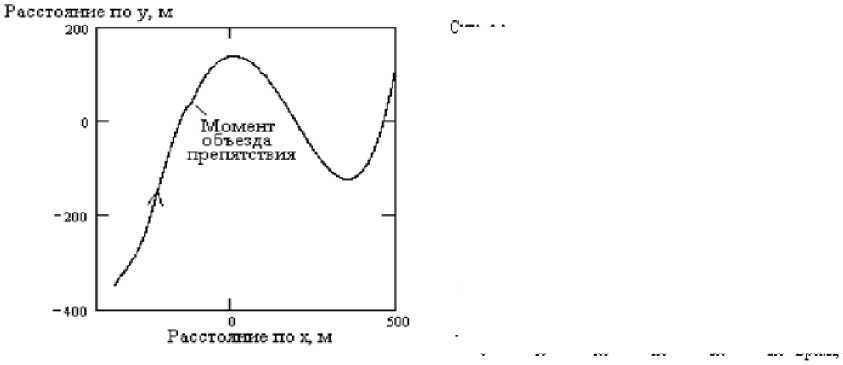
Рис 9а. Общий вид траектории при объезде препятствий

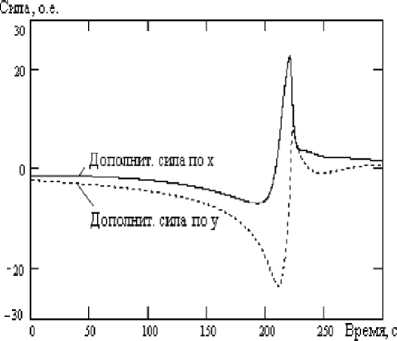
Рис 9б. Взаимодействие сил по х и по у

Движение длилось 300 секунд. Из рисунка видно, что вид траектории в целом отслеживается.

Расстояние по у, м

100 ----------г-

Момент объезда препятствия

50 -

0 -

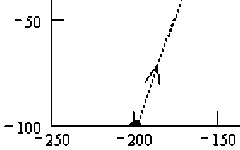
Рис. 10 – Фрагмент траектории вблизи препятствия

-100      -50 о

Расстояние по ^ м

БТС объезжает препятствие снизу справа, скорость снижается до 2 м/c. После ухода от препятствия скорость быстро нарастает.

Выводы

Представлено разработанное упрощенное математическое описание движения беспилотных транспортных средств в виде системы четырех уравнений в различных условиях движения. Обоснован выбор средств описания заданной траектории движения на плоскости в земной системе координат. Показано, что применение метода наименьших квадратов позволяет с достаточной точностью определять коэффициенты аппроксимации траектории, заданной опорными точками. Предложен способ управления, позволяющий удерживать движущееся транспортное средство на заданной траектории. Способ основан на оценке отклонения траектории от заданного вида и соответствующей корректировке меридиальной составляющей силы движения.

Ввиду нестабильной скорости движения разработан способ поддержания скорости на желаемом уровне за счет корректировки тангенциальной составляющей силы. Предложенные способы обеспечивают приемлемое качество движения по заданной траектории.

Описан метод имитации реального рельефа поверхности, по которой движется транспортное средство. Показано, что при движении по холмистой поверхности возникают дополнительные силы то ускоряющие, то замедляющие движение. Предложенный метод управления позволяет свести к минимуму влияние этих сил.