Автоматизация формирования монтажей горячекатаного проката металлургического производства

DOI:

ул. Московская, 30, 398055 г. Липецк, Российская Федерация

Горячекатаный прокат [5; 8; 12] является одним из востребованных материалов во многих отраслях промышленности. Сортамент горячекатаного проката не подвержен коррозии, очень выгоден в соотношении цены и качества, получается пластичным при сохранении высоких показателей прочности, почти не требует обработки, устойчив к высоким температурам и механическим повреждениям [19].

Прокатка металла на непрерывном широкополосном стане реализуется монтажными партиями [15], для обеспечения требуемого качества которых накладывается целый ряд технологических ограничений [2; 3; 9]. Кроме характеристик качества важнейшим показателем производства, в том числе горячего проката, является производительность [6]. В этом случае оптимизация производства заключается в таком планировании монтажных партий, которое минимизирует общее время их прокатки, то есть увеличивает производительность, при соблюдении всех задаваемых ограничений, влияющих на качество проката. Таким образом, разработка методов оптимизации, а также внедрение новых методов формирования монтажных партий на станах горячего проката является одной из актуальных тем исследования.

1. Формализация задачи и методология исследования

Разработанный алгоритм формирования монтажей учитывает накладываемые ограничения и максимизирует установленный критерий качества. В качестве входных данных используется информация о наличии и характеристиках слябов на складе. Для реализации алгоритма был использован блок программирования математического пакета Mathcad [7]. Оптимизация реализована за счет применения генетических алгоритмов [1; 10; 11; 13; 14; 16; 18; 20].

Далее представлена формализованная постановка задачи. Имеется набор векторов X = { Х 1 ,..., Х _п } , состоящий из слябов Х _г . Необходимо составить такую последовательность выполнения заказов УЦХ) на прокатку на стане, чтобы достичь максимальной производительности прокатки V сформированных монтажных партий. Под производительностью подразумевается отношение длины прокатываемой полосы к продолжительности процесса.

Введем следующие обозначения для описания слябов и монтажей:

х _г =

Ж 1

.    , Y_u =

Х 13

X _r

.

.

.

Y

m

где г = 1,..., n; n — количество слябов; u — номер монтажной партии; г и т — соответственно первый и последний элементы монтажной партии; ж / — параметр, несущий в себе информацию о слябе, I = 1... 13.

Из полученного со склада массива данных о имеющихся слябах производится отбор необходимых параметров, убираются строки с отсутствующими данными, а также заведомо неверные. В конечной выборке используются следующие параметры слябов:

• •    ж 1 — время прокатки сляба (с);

• •    ж ₂ — марка стали;

• •    ж ₃ — группа отделки поверхности;

• •    ж₄ — маршрут;

• •    ж ₅ — толщина сляба (мм);

• •    х₆ — ширина сляба (мм);

• •    х₇ — длина сляба (мм);

• •    ж₈ — вес сляба (т);

• •    х₉ — целевая толщина рулона (мм);

• •    ж ₁₀ — целевая ширина рулона (мм);

• •    х 11 — длина полосы (м);

• •    ж ₁₂ — цех назначения;

• •    ж ₁₃ — примечание.

Целевая функция:

V(Y i ,...,Y . ) = 1 £ v(r . ) = i £ ^ ^ max,            (1)

2 "     2 " V-)

где 2 — количество монтажей; v — производительность u-й монтажной партии; d — общая длина проката u-й монтажной партии; t — общее время на прокатку всех слябов u-й монтажной партии.

Время на прокатку считается по формуле:

t = х 1 + tp,

• 120,    if (^_W, _w = ^_W, _w +i ),

  tp = <

  
  

• 60,    if (^ 9, _ш = Х 9, _ш +1 ) Л (ж_ш , _№ = ^ io, _w +i ), 0 ,

где tp — время на перенастройку стана; w — порядковый номер сляба в u-й монтажной партии.

С учетом описанных в [9] ограничений для монтажных партий должны выполняться условия G(Y(X )):

( q Е ^8,w < 4000, W = 1 G(Y (X)) = < ^10,w+1   ^10,w < 250, ^9,w+1   ^9,w < 1.5, q E ^11,W < 40000, (xw,w = ^W,w+1) Vw = 1,..., q, . W = 1 где q — количество слябов в n-й монтажной партии.

Весь массив считанных данных разбивается на следующие подвыборки, которые обладают установленными для них условиями:

• 1)    Rabv — настроечный металл после перевалки рабочих валков;

• 2)    кт7_60 — по длине монтажа от 7 до 60 км;

• 3)    кт97 — по длине монтажа до 97 км;

• 4)    кт120 — по длине монтажа до 120 км;

• 5)    кт121 _ — по длине монтажа после 120 км.

Из полученных подвыборок составляются монтажные партии в соответствии с технологическими ограничениями для данных групп. Также в каждом монтаже учитывается ряд ограничений, накладываемых на весь монтаж.

Схема разработанного алгоритма изображена на рисунке 1.

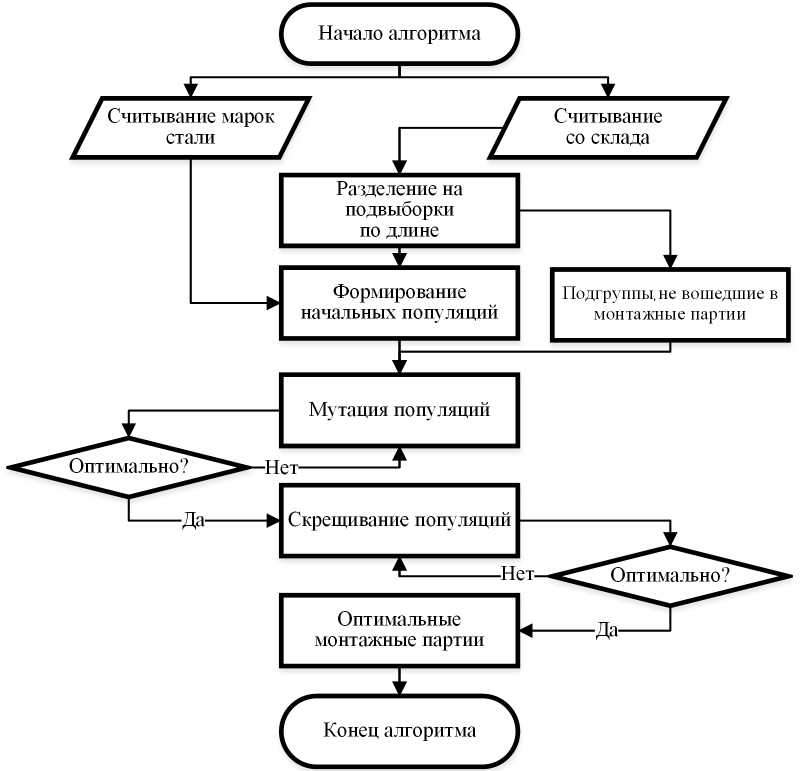
Рис. 1. Блок-схема программы

Реализация алгоритма оптимизации происходит следующим образом. Считывание из файла Excel подготовленной выборки. Полученные данные сортируются по ширине полосы — от широкого к узкому. Также выполняется считывание марок стали, относящихся к определенным группам: uglPDS — подкат углеродистой стали для ПДС; xolkS — марки холоднокатаной стали; tovarS — марки товарной стали; electrS — марки электротехнической стали [4]. Данные группы марок требуются при формировании монтажей для соответствия накладываемых технологических ограничений.

На первом шаге генетического алгоритма производится составление начальных популяций с целью комплектации слябов со склада в монтажные партии. Формирование монтажей прекращается при отсутствии слябов в любой из подвыборок. Так, монтажи составляются последовательно один за другим и имеют следующий вид:

f    Ji • • •          Jg Di • • •        Dg М1 • • •      Mg / ji montti = Т1 • • •         Тд , J = 1   . k1 • • •           kg \ jk У1 • • •          yg ⎠ ^ ogshDL 1 • • • ogshDLg где montu — сформированный монтаж; g = 1, ... 5 — номер подвыборки; Jg — вектор-столбец с порядковыми номерами выбранных в данный монтаж слябов со склада; к — это количество слябов в подвыборке g монтажа u; Dg — общая длина монтажа в подвыборке g с учетом предшествующих подгрупп (мм); Mg — общая масса монтажа в подвыборке g с учетом предшествующих подгрупп (т); Тд — общее время проката всех слябов монтажа в подвыборке g с учетом предшествующих подгрупп (с); yg — строки выбранных слябов в подвыборке g; ogshDLg — суммарная длина следующих друг за другом слябов одинаковой ширины.

Составленные в соответствии с технологическими ограничениями монтажные партии объединяются в набор монтажей. Слябы, не попавшие в монтажные партии, распределяются в подвыборки той же структуры, что использовались при формировании начальных популяций генетического алгоритма. Они будут называться свободными подвыборками.

Схема формирования начальных популяций показана на рисунке 2.

Фрагмент полученных начальных популяций (монтажей) представлен на рисунке 3.

Следующим шагом будет мутация полученного набора монтажей. Оператор мутаций меняет произвольное число элементов в особи на другие произвольные. Фактически он является неким диссипативным элементом, с одной стороны вытягивающим из локальных экстремумов, с другой — приносящим новую информацию в популяцию. Схема мутации популяций изображена на рисунке 4.

В условиях решаемой задачи оператор мутаций будет менять произвольно выбранное количество подвыборок из монтажей со случайными свободными подвыборками. Мутировавшие монтажи объединяются в набор и так получаются несколько особей. Среди имеющихся особей потомков выбирается наиболее приспособленная, то есть набор монтажей с наибольшей производительностью (1), который станет родителем для следующего поколения мутантов. Цикл повторяется до тех пор, пока производительность новых поколений не будет меньше или равна производительности их предка. При этом проводится проверка монтажей внутри набора на соответствие введенных ограничений. Лучший набор монтажей, полученный с помощью мутаций, проходит через скрещивание среди монтажей, вошедших в этот набор. Свободные подвыборки отбрасываются.

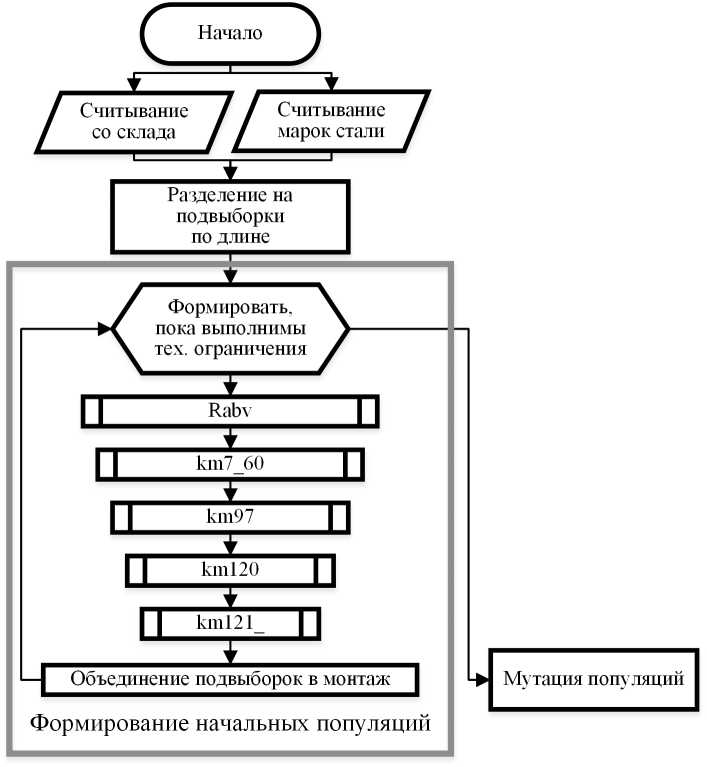
Рис. 2. Схема формирования начальных популяций

	' {9,1}	{50.1}	{33,1}	{35,1}	{28,1}
	3 6.403 x 10	5.996 x 104	4 9.658 x 10	1.195 x IO5	1.36 x IO5
	276.73	1.61 x 103	2.49 x IO3	3 3.316 x 10	3.951 x 103
mont,„ =	3	3	3	4	4
w	1.01 x 10	5.561 x 10	8.743 x 10	1.091 x 10	1.305 x 10
	9	50	33	35	28
	{9,1}	{50.1}	{33,1}	{35,1}	{28.1}
	3 ( 6.403 x 10	1.276 x 104	8.953 x IO3	,          4 3.185 x 10	8.209 x 103;

Рис. 3. Фрагмент полученных начальных популяций

В данном генетическом алгоритме применяется равномерное скрещивание, иначе называемое монолитным или одностадийным, выполняется в соответствии с заранее выбранным эталоном, который указывает, какие гены должны наследоваться от первого родителя (остальные гены берутся от второго родителя).

Схема скрещивания популяций представлена на рисунке 5.

Случайным образом из набора мутировавших монтажей выбираются попарно особи для выполнения оператора скрещивания:

в которых происходит следующая замена:

mont e = ( [Rabt] _a mont a = ( [Rabt ] _b

[km7_60] _b [km97] _a [fcm120] _b [km121 _ \ _a

[fcm7_60] _a [fem97] ₆ [A;m120] _a [km121 _ \ _b

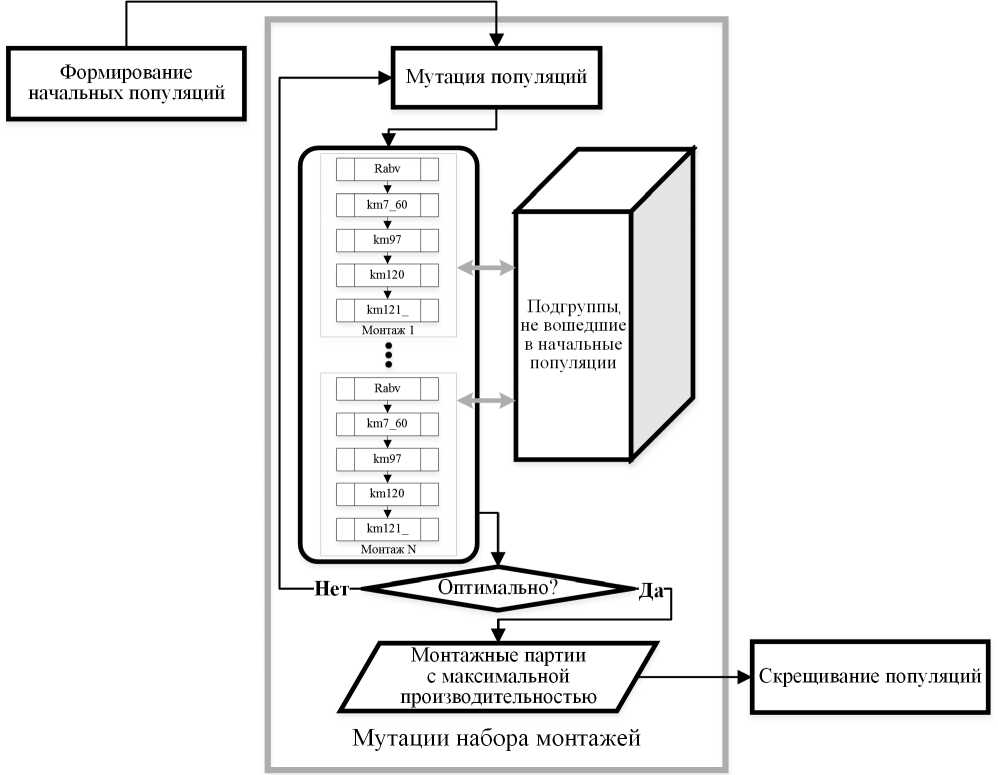
Рис. 4. Схема мутаций популяций

Полученные монтажи являются новым поколением особей. Они снова объединяются в набор. Таким образом формируется несколько случайно скрещенных наборов. Критерий останова скрещивания совпадает с критерием останова при мутации (1). По окончанию работы оператора скрещивания будет найден оптимальный набор монтажных партий, который является результатом работы генетического алгоритма.

2.    Интерпретация и анализ результатов исследований

Проведено исследование по работе реализованного алгоритма. Проверка проводилась на данных о слябах со склада цеха горячей прокатки. Из полученных сведений была отобрана необходимая для работы алгоритма информация.

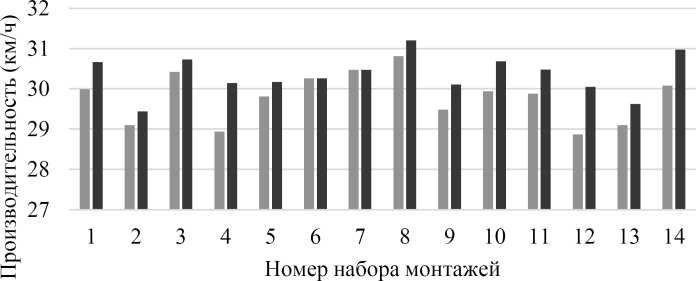
С помощью программы формирования монтажных партий горячекатаного проката обработана информация о 276 000 слябах, располагавшихся на складе в течение года, в результате чего получено 14 уникальных наборов монтажных партий. Каждый набор сформирован на непересекающихся диапазонах входных данных по 20 тысяч выборок в первых 13 наборах и 16 тысяч в последнем. Общая информация по наборам представлена в таблице.

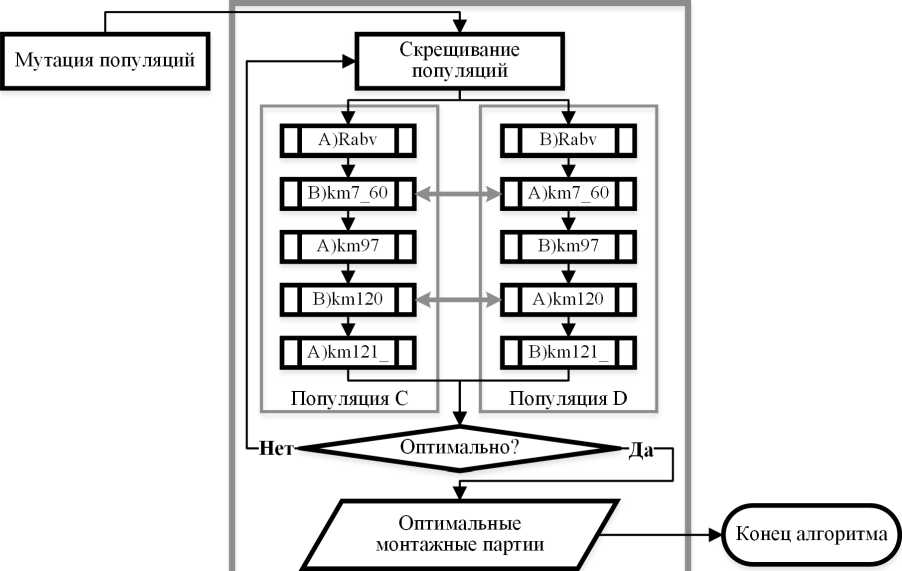
Скрещивание набора монтажей

Рис. 5. Схема скрещивания популяций

В таблице № — это номер набора, Кт — количество монтажей в наборе (шт), Кр — количество проката в наборе (шт), Ln — общая длина проката в наборе (км), Мп — общая масса проката в наборе (т), Тр — требуемое на прокатку время (ч), Vn — производительность набора после применения генетических алгоритмов (км/ч), AVn — прирост производительности проката после применения генетических алгоритмов (км/ч).

Средний прирост производительности составил 0,56 (км/ч), что говорит о релевантности используемого метода формирования и оптимизации составления монтажных партий на станах горячего проката. Больший эффект на изменение производительности оказал оператор мутации. Сравнение производительности наборов монтажей до и после работы генетического алгоритма показано на рисунке 6. Всего алгоритмом было получено 507 монтажей средней производительностью 30,34 (км/ч), что соответствует повышению эффективности прокатки на 1,9 %.

Заключение

Таким образом, в работе была представлена формализованная постановка оптимального формирования монтажных партий на стане горячей прокатки. Предложен генетический алгоритм решения задачи. Приведено описание операций формирования начальных популяций (наборов монтажей), мутаций и скрещивания. Алгоритм учитывает технологические ограничения, накладываемые на производственный процесс. Критерием оптимальности является получение максимальной производительности набора монтажей, которая достигается за счет уменьшения времени на перестройку оборудования при переходе на разные ширину и толщину проката. Была проведена проверка адекватности результатов автоматического формирования монтажных партий на реальных данных со склада слябов. На основании полученных результатов работы алгоритма видно, что раз- работанный автоматизированный подход оптимального формирования монтажных партий на стане горячей прокатки металлургического производства позволяет увеличить производительность стана и снизить расход энергоресурсов.

Сведения по наборам монтажей

№	Km	Kp	Ln	Mn	Tp	Vn	Δ Vn
1	40	5952	5626,81	143772,51	183,50	30,66	0,68
2	42	6360	5830,02	155523,89	198,06	29,44	0,34
3	41	6118	5726,41	147124,89	186,37	30,73	0,31
4	35	5367	5014,91	129461,26	166,36	30,14	1,21
5	32	4702	4446,35	113782,32	147,38	30,17	0,36
6	37	6012	5678,48	146602,34	187,64	30,26	0,00
7	40	6547	6141,22	158462,54	201,55	30,47	0,00
8	37	5640	5358,69	135655,05	171,73	31,20	0,39
9	43	6399	6016,90	158217,29	199,88	30,10	0,62
10	38	5677	5348,68	140675,45	174,30	30,69	0,74
11	34	5040	4742,33	124922,34	155,59	30,48	0,60
12	28	4092	3929,63	102252,99	130,77	30,05	1,18
13	35	5260	4910,13	127793,26	165,73	29,63	0,53
14	25	3701	3558,23	91074,60	114,88	30,97	0,89

■ Начальные популяции   ■ Результат работы Г А

Рис. 6. Производительность (км/ч)