Автоматизация контроля качества гомогенизации молока методами ультразвуковой спектроскопии

Ребриков Д.И., Мерзликин В.Е., 2015

Технологический процесс гомогенизации молока и молочных продуктов необходим для повышения дисперсности в них жировой фазы, что исключает отстаивание жира в процессе хранения и транспортировки, окислительные процессы, дестабилизацию и подсбивание при интенсивном перемешивании и транспортировании. Под степенью гомогенизации принято понимать средний размер жировых шариков, степень устойчивой во времени однородности (гомогенности), то есть отсутствие микроконцентрацион-ных неоднородностей, образующихся при смешивании взаимно нерастворимых веществ [1].

Молоко и молочные продукты, как правило, представляют собой полидисперсную многофазную систему, включающую дисперсию молочного жира, коллоидную систему казеиновых частиц, дисперсию липопротеиновых частиц, растворы сывороточных белков, низкомолекулярных азотистых соединений, лактозы, солей и других соединений. Средний размер жировых шариков в сливках оказывает существенное влияние на процесс маслообразования.

В подавляющем большинстве промышленных технологических процессов гомогенизации используется гомогенизация молока при продавливании его через кольцевую клапанную щель гомогенизирующей головки машины. Жировые шарики, проходя через эту щель, разрушаются (диспергируются). Необходимое для гомогенизации давление создается насосом.

Оценка степени гомогенизации продукта проводится после полного цикла пропускания всей массы молока через гомогенизирующую головку при заданном давлении, и в случае недостаточной степени гомогенизации осуществляется повторение полного цикла. Это приводит к значительным энергетическим затратам и, следовательно, к повышению себестоимости конечной продукции. Для решения этой проблемы необходим оперативный контроль степени гомогенизации и изменения параметров процесса (давления и температуры) для гарантированного достижения заданной степени гомогенизации в течение одного цикла.

Существующие способы контроля степени гомогенизации относятся, как правило, к лабораторным, а их время цикла анализа вместе с отбором пробы сопоставимо со временем нанесения управляющих воздействий и компенсации возмущений. В настоящее время эффективность гомогенизации оценивают методами, условно разделяемыми на группы: мик- роскопическое определение, седиментационный анализ и фракционный анализ с использованием лазерной дифракции. С точки зрения автоматизации процесса гомогенизации первые два метода обладают существенным запаздыванием, а второй требует автоматизации пробоотбора и обеспечения оптической проницаемости среды.

Наряду с прямыми методами контроля, использующими визуальное наблюдение и определение степени гомогенизации по специальным методикам, существует ряд косвенных методов, использующих связь поддающихся измерению физических величин, коррелирующих со степенью гомогенизации [2]. Одним из удобных для практического применения способов косвенного контроля степени гомогенизации и других свойств молочных продуктов являются ультразвуковые (УЗ) методы контроля. На базе этих методов созданы лабораторные анализаторы, использующиеся в молочной отрасли [3, 15, 16, 17].

Используя в качестве основы измерительной системы УЗ принцип, возможно создать способ непрерывного измерения степени гомогенизации и синтеза замкнутой системы регулирования этого параметра изменением давления или перераспределением потоков между гомогенизирующими головками, обеспечивающими заданную степень гомогенизации.

Измерение степени гомогенизации с использованием УЗ основано на связи акустических свойств среды (скорости звука с, коэффициента поглощения а при определённой частоте УЗ воздействия и температуре), его вязкоупругих характеристик (компонентов комплексного модуля упругости E (^)) и структурно-молекулярных свойств. Непрерывное измерение акустических свойств реализуется с помощью УЗ излучателя и приемника, позволяющих излу- чать и принимать прошедшие через исследуемую среду акустические импульсы. По парамет- рам излученных и принятых импульсов рассчитывают акустические свойства среды [4]:

h 1 А c = -, а = - • ln -из^ , t    hAпр , где h – расстояние между поверхностями излучателя и приемника, м; t - время прохождения импульса, с; A – амплитуда сигнала, подава- емого на излучатель; Aпр – амплитуда сигнала на приемнике, В.

Существующие УЗ измерители степени гомогенизации обычно основаны на интеграль- ной оценке этого показателя по косвенным измерениям (вязкости, плотности, скорости осаждения и т.д.) и расчету степени гомогенизации по эмпирическим формулам [6].

Такой подход не позволяет выявить вид функции распределения жировых шариков по фракциям (массе или объему) или хотя бы его основные статистические моменты, так как суммарный вклад может давать одинаковый эффект при разных видах подынтегральной функции (3). В то же время именно однородность, характеризуемая функцией массового и объемного распределения элементов жировой фазы по фракциям, является показателем эффективности осуществления процесса гомогенизации. Из рисунка 2 виден характер распределения, который представлен гистограммой частот попадания жирового шарика в диапазон объемов (масс, диаметров и т.п.). Такое распределение дает более полную картину о степени гомогенизации по сравнению с известными методами экспресс-оценки степени гомогенизации, так как позволяет учесть разброс размеров отдельных элементов жировой фазы. Наличие информации о распределении помогает выявить возможные крупные элементы жировой фазы, оставшиеся после процесса гомогенизации, так как при использовании интегральных оценок они могут быть скомпенсированы более мелкими элементами.

Одной из областей применения методов акустической спектрометрии является оценка размеров частиц и их распределения по размерам [5, 6]. Акустические свойства среды a, c позволяют определять компоненты комплексного модуля упругости и их частотные характеристики [7]:

E (—) = E' + iE ” = E' + iton =

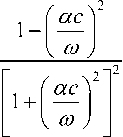
a c

+ i • 2 pc²-- ^— ----2

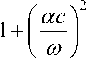
,.(1)

где — - частота, Гц; E \ E " - действительная и мнимая части комплексного модуля упругости, Па; П - динамическая вязкость, Па • с ; p - плотность, кг/м³.

Компоненты комплексного модуля, в свою очередь, определяются в соответствии с феноменологической релаксационной теорией свойствами структурных единиц, составляющих исследуемую среду и характеризующи- мися временами релаксации т :

~ , _х         Nr E — Т :

E (—) = E0 '! j^T + j=1 1 + — Т •

j

+ i—

, Nr    пj п^+L- j=11 + — Т j

где E_o - равновесный модуль упругости;

Ej - модуль упругости j-го релаксационного механизма; п — нерелаксирующая вязкость; Пj - вязкость j-го релаксационного механизма; тj = Ej [пj - время релаксации j-го релаксаци- онного механизма.

В общем случае число элементов беско- нечно велико, а значения периодов релаксации могут описываться некоторой непрерывной функцией распределения. При таком способе описания уравнение релаксации имеют вид [6]:

~ х X *^       х    —² Т²

E(—)= J H(т)----d 1пт +

-ю     1 + — т

+if H (т) ——Т . d 1пт

i V Ч + —2 т т

,

где H (т) - функция плотности спектра времен релаксации (релаксационный спектр).

Таким образом, появляется возможность непрерывно получать оценки такого показателя качества, как среднее время релаксации всех вовлекаемых в колебательное движение структурных единиц или плотность спектра времен релаксации, характеризующую распределение этих структурных единиц по их времени релаксации, которое в свою очередь связано с их массой. Для этого необходимо осуществлять изменение частоты воздействия в ходе измерений.

Получение в аналитическом виде функции H ( т ) возможно при аналитическом задании функций E ’(—) , E ”( — ) в интервале [ -^, ^ ] . Так как на практике это чрезвычайно трудно осуществить, то часто пользуются приближенными методами [8].

В случае экспериментальных исследований используется дискретный спектр времен релаксации, соответствующий дискретному набору частот исследования. Существует множество подходов к его определению. Так в [8] приведены методы вычисления приближенных значений дискретного спектра времен релаксации, основанные на использовании графической зависимости логарифма упругого модуля от логарифма частоты. Данные методы требуют достаточно малого шага дискретизации по частоте и высокой точности измерения упругого модуля, в противном случае они могут дать некорректный результат.

В другом источнике [7] приведен прямой метод расчета релаксационного спектра. Метод состоит в определении пар величин Ei -Hi. Пары Ei -Hi варьируются, и рассчитанные значения E'са1с(ю) и E"са1с(ю) сопоставляются с экспе риментальными данными E ’ехр(ю) и E ”ехр(ю).

Расхождение между экспериментом и результатами расчетов (получаемыми при варьировании пар E i -H i ) оценивается функционалом ошибок. Эта величина может рассчитываться различным образом. Известен также [8] метод линеаризации, который основан на представлении зависимостей E '(ю) и E "(ю) или релаксационной функции, экспериментально измеренных в некоторых пределах в виде степенных рядов по переменной ω . В противоположность описанному выше методу, в данном случае минимизация функционала ошибок становится линейной задачей, и поэтому определение коэффициентов имеет однозначное решение.

Также в [7] приведен метод регуляризации, который обсуждался во многих работах [9, 10]. Этот метод представляет собой частный случай решения так называемых интегральных уравнений Фредгольма первого рода. Все обратные за- дачи определения времен релаксации относятся к задачам этого типа. Один из наиболее общепри- нятых методов решения таких задач основывается на методе регуляризации Тихонова [11]. Метод заключается в минимизации критерия V(Я):

N

V (2) = Е — i=1 ст

E .

V

(            V?

J F ( t, , т )------ dт

I I t            ^Т     jj

+

,   (4)

+2|LH|\2т е It где Я - параметр регуляризации; оператор L выбирается обычно из условий (LH=H или (LH= H ”); ст - ошибка; It - множество значений времен релаксации т.

При реализации экспресс-методов контроля, нежелательно использовать численные методы, а также процедуры регуляризации, так как их использование в режиме реального времени приводит к трудно прогнозируемому увеличению длительности цикла анализа, а также в отсутствии несходимости того или иного метода. В таком случае следует вводить допущения, позволяющие с небольшой потерей точности расчетов получать аналитические зависимости спектра времен релаксации от вязкоупругих характеристик.

Так как функция плотности спектра времен релаксации входит в действительную и мнимую части модуля упругости достаточно иметь информацию об одном из компонентов модуля. Для жидкостей удобнее использовать модуль потерь E". Одним из способов приближенного аналитического описания спектра времен релаксации по известному спектру E"(ю) показан в [7].

По определению, плотность спектра времен релаксации Н(т) , умноженная на dT имеет смысл суммарной вязкости всех максвелловских механизмов, времена релаксации которых заключены в интервале от т до т+dT .

Способ заключается в использовании до- ют пущения о том, что выражение ----5—т

1 + ют ² аппроксимируется б -функцией. В силу свойств б -функции:

то

J 5 ( x ^- x о ) f ( x ) dx = f ( x о ) ,        ⁽⁵⁾

-TO можно записать мнимую часть комплексного модуля упругости как:

T H ( т ) ютd ( ютА

E ”⁽ю) = юп⁽ю) = юп_ж + J---—V2 ~

₀ ют 1 + ют

( 1Л

« ^юП « ⁺ H I - I

V ю j

Таким образом, в этом приближении релаксационный спектр можно аппроксимировать частотным спектром модуля потерь комплексного модуля упругости E :

H(т) = ю(п(ю)-7, )|и =1 .

т

Пренебрегая п , ^в соответствии с [7]:

H (т) = юп(ю)| ^ = E" (ю)^ 1.(8)

тт

Таким образом, для определения дискретного спектра времен релаксации, т.е. множества значений Н ( т ), необходимо измерить множество значений E "ю ) . Значение модуля потерь может быть рассчитано с использованием формул (1), (2) по измеряемым акустическим параметрам среды: коэффициенту затухания и скорости распространения ультразвука.

Интерпретация значений времени релаксации определяет связь их с показателями качества. Поскольку это время показывает инерционность структурного элемента, то в первую очередь оно характеризует его массу. Также в дисперсной среде колебания под действием акустического импульса сопровождаются диссипативными потерями за счет вязкого трения, то есть связано с размерами, формой, плотностью и «протекаемостью» этих структурных единиц.

В работах [12, 13] использованы подходы к оценке масс, вовлекаемых в колебательное движение по временам их релаксации. Одной из форм связи массы структурного элемента и его времени релаксации является вид:

т = к ■ m ^e , (9) где к - коэффициент пропорциональности; в - показатель степени, близкий по значению к показателю степени, характеризующему влияние молекулярной массы растворов полимеров на его вязкость [12].

Таким образом, измерение распределения акустических свойств молока по частоте, оценка по ним функции плотности спектра времен релаксации, а затем переход от времен релаксации к массам частиц позволяют осуществлять оперативный контроль распределения масс жировых шариков по фракциям.

Для проведения исследований были проведены следующие действия (рисунок 1) [18, 19]:

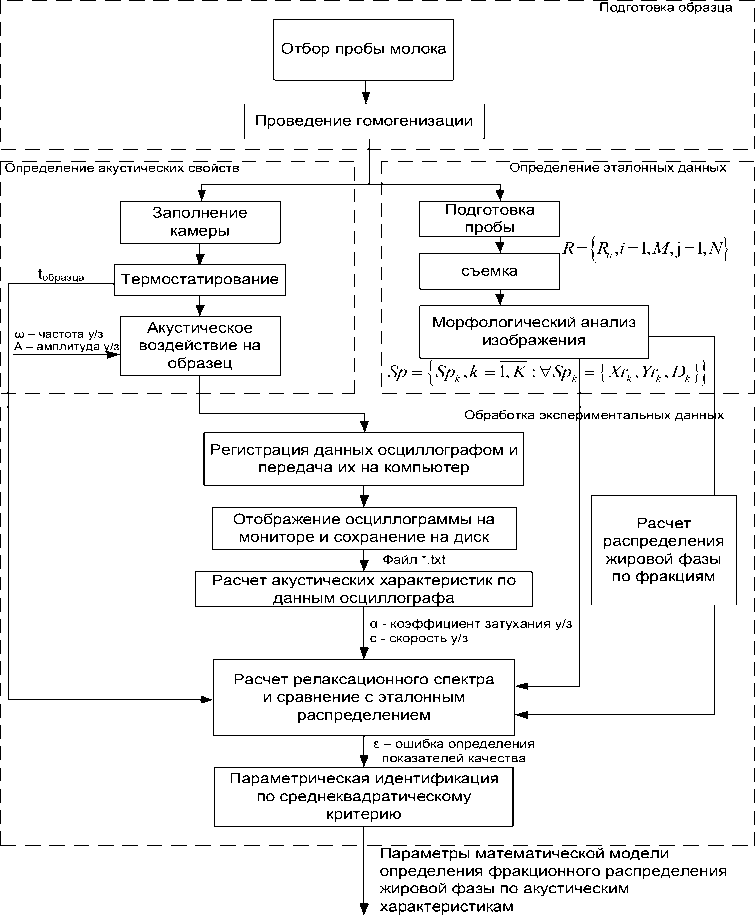
Рисунок 1. Методика проведения экспериментальных исследований

• 1.    Осуществление микросъемки образцов молока с разной глубиной обработки на гомогенизаторе и получение множества R = { R , i = 1, M ,j = 1, N } ,где i - номер пикселя по горизонтали, j - номер пикселя по вертикали.

• 2.    Проведение процедуры морфологического анализа изображения и получение множества выделенных объектов соответствующих жировому шарику

• 3.    Построение гистограмм, описывающих распределение жировой фазы по массам в исследуемом объеме.

• 4.    Построение аппроксимирующей это распределение функции f ( m ) для формирования модели непрерывной зависимости данных для дальнейших исследований.

• 5.    Ультразвуковой анализ этих же образцов молока в доступном частотном диапазоне и построение частотных характеристик модуля потерь E"(to ) и функции плотности спектра времен релаксации H ( т ) .

• 7.    Изучение корреляции плотности спектра времен релаксации и аппроксимирующих гистограммы функций.

• 8.    Построение алгоритма расчета распределения жировой фазы по массам в исследуемом объеме введением масштабных коэффициентов.

  

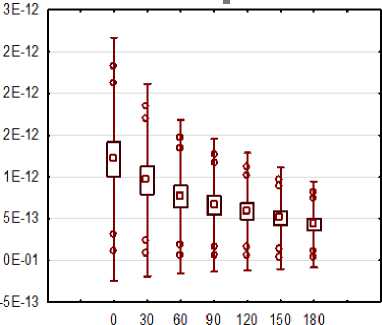
  давление, МПа

  - среднее значение; - среднее значение ± стандартная ошибка; среднее значение ± 2* стан

  дартное отклонение;       - выбросы.

  Рисунок 2 Распределение жировых шариков по размерам, для образцов в ходе процесса гомогенизации.

  
  

Sp = {Spk, к = Гк: vSpk = {Xr, Yrk, Dk }}, где k, Xrk, Yrk, Dk - порядковый номер, координаты и диаметр шарика.

Предварительная экспериментальная проверка сделанных предположений осуществлялась на образцах в разной степенью гомогенизации, которая достигалась за счет изменения давления в гомогенизаторе (4, 8, 12 МПа). План проведения исследований представлен на рисунке 1. Распределение жировых фракций представлено на рисунке 2. Для определения частотного распределения модуля потерь использовалось «прозвучивание» образцов молока с использованием сигнала «белый шум» (схема экспериментальной установки на ри- сунке 3) и расчет релаксационного спектра в соответствии с (10). Параллельно проводилось 4 измерения при температуре 18 0С.

Фторопластовая вставка

Цифровой о сциллограф

Пьезоэлектрический преобразователь стальная пластина

Цифровой генератор

!

1»

Рисунок 3 Экспериментальная установка проведения исследований

Для формализации связи между момен- тами распределения жировых шариков по диа- метру и релаксационного спектра использована зависимость вида:

^{f ( x} ) =

Р¹ x + ql

- для первого момента;

pl- x2 + p 2 • x + p 3 f (x) =  -------------— для второго момента, x + ql параметры которых представлены в таблице.

На рисунке 4 и 5 представлена связь первых и вторых (соответственно) моментов распределений жировых шариков по диаметру и релаксационного спектра.

Т а б л и ц а 1

Параметры математической модели для описания моментов

Параметр модели	Д 1	Ц 2
p 1	0.001533	4.986
p 2	-	-2.365
p 3	-	0.2806
q 1	-18.15	-0.225
СКО	0.00063	0.000056
Коэф. парной корреляции	0.9924	0.9936
Скорректированный коэф. парной корреляции	0.9908	0.9872
Среднеквадратичная ошибка	0.01126	0.0043

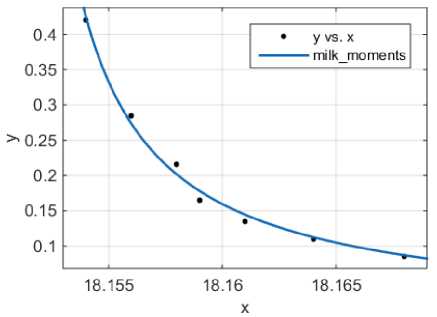
Рисунок 4. Связь первых моментов распределений жировых шариков по диаметру и релаксационного спектра

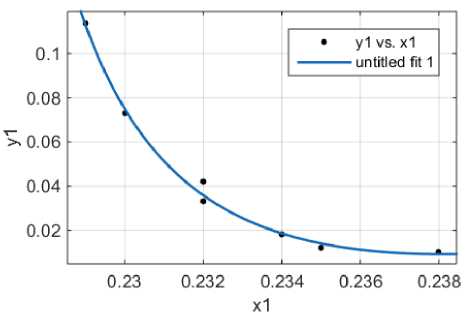
Рисунок 5. Связь вторых моментов распределений жировых шариков по диаметру и релаксационного спектра

Проведенные исследования показали принципиальную возможность реализации УЗ способа контроля качества процесса гомогенизации молока и оценки распределения фракций жировой фазы. Полученные оценки релаксационных спектров говорят о тесной связи первых двух моментов распределений жировых шариков по диаметру и релаксационных спектра (0,98 для первого момента и 0,9 для второго). Кроме того, ввиду зависимости времени релаксации от температуры представляется целесообразным для повышения метрологических характеристик предложенного метода провести исследования при различных значениях температур.