Автоматное представление молекул типа фуллерена

Автоматы занимают важное место в информатике (или, как сейчас принято говорить, Computer science). Многие, в том числе и весьма, крупные, геометрико-алгебраические проблемы решаются или переписываются па. языке теории автоматов. Наиболее полно алгебраический контекст автоматов отражен в обзоре Григорчука. [1].

В данной работе мы рассматриваем конечный полуавтомат [2], который устроен невероятно просто. Речь идет о головоломке 2х3-пазл. Граф данного полуавтомата, построенный в программе Gephi, имеет частичное сходство со структурой молекулы фуллерена. С60.

• 1.    Головоломка пазла 2x3

Рассмотрим 2х3-пазл. состоящий из пяти пронумерованных цифрами 1, 2, 3,4, 5 фишек и пустой клетки. Как обычно, пустая клетка, может перемещаться по игровому полю. Изъятия фишек запрещены. Данная головоломка моделируется конечным полуавтоматом А = (S, А, 5) с множеством состояний S С 8б, на вход которого подаются слова алфавита А = {1, 2, 3, 4, 5}, 8б — симметрическая группа перестановок на множестве {0,1,2, 3,4, 5}, где сим волом «0» мы обозначили пустую клетку, а 5 = S хА ^ S — функция перехода. Каждой конфигурации пазла ставится в соответствие перестановка, получаемая выписыванием, сначала, трех элементов первой строки слева направо, а затем трех элементов второй строки справа налево (рис. 1).

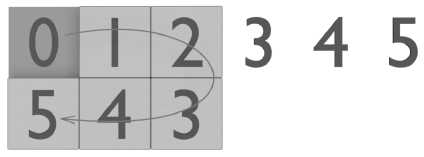
Рис. 1. Конфигурация пазла 2x3.

Четность перестановок из S5, выписанных без учета «0», является инвариантом игры. Элемент а₀ (где а₀ = (1, 2,3,4, 5,0), а₀ Е S6) будем считать принадлежащим множеству S. Получаем соотношение |S| = |S₆1/2. Данная статья посвящена изучению алгебры и геометрии множества S, не являющегося, например, подгруппой Se. Более точно, мы хотим указать на некоторую связь между молекулой фуллерена С60 и графическим изображением множества S (рис. 2).

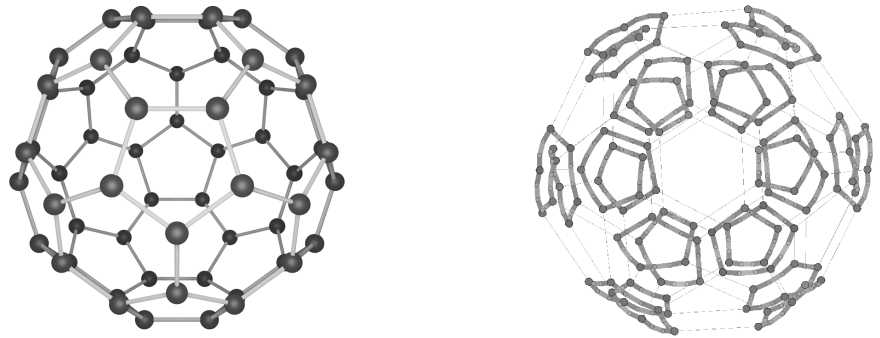
а)                                                            Ь)

Рис. 2. а) фуллерен С60; Ь) граф пазла 2x3.

Множество S обладает следующими очевидными свойствами:

• •    |S | = 6!/2;

• •    S распадается на 12 непересекающихся множеств по 30 элементов в каждом;

• •    каждое множество S^к, к = I, II, ... ,XII задается замкнутой последовательностью из 30 шагов, получаемых движениями пустой клетки вдоль линии обхода игрового поля. Графы таких множеств можно представить в виде кольца с 30 вершинами (рис. 3), поэтому в дальнейшем будем называть их кольцами.

• 2.    Визуализация графа S

Количество колец S^к будет в действительности ровно 12. Перестановки в пределах одного кольца а^к Е S^к исчерпываются циклическими сдвигами а^к и всевозможными размещениями нуля. Следовательно, |S ^к | = 5х6 = 30. Делим теперь |S|/|S ^к | и получаем, что количество различных колец равно 12.

Если считать перестановки из S вершинами некоторого графа, то они распадутся на два вида: вершины степени 2 и степени 3.

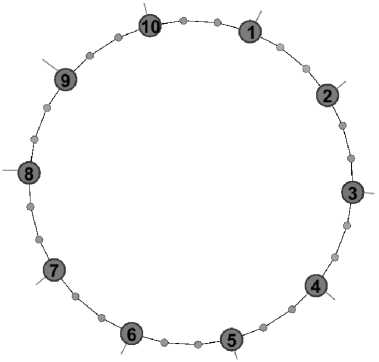
Рис. 3. Граф кольца S^J, где 10 вершин степени 3 выделены пурпурным цветом, а вершины степени 2 — зеленым.

Для визуализации структуры графа из 360 вершин множества S использовалось ПО Gephi (вер. 0.9.2), со встроенным алгоритмом ForceAtlas 2. Были получены следующие варианты изображения графа пазла 2x3 (рис. 4). На рис. 4.1 представлены все двенадцать взаимосвязанных колец в развернутом виде. Для большей наглядности изображения графа вес ребра между вершинами внутри колец был принят в 10 раз больше веса ребра соединяющего вершины смежных колец, а так же вершины степени 2 выделены зеленым цветом, а степени 3 пурпурным цветом и большего размера.

При изменении параметров алгоритма, можно получить два изображения графа S схожего со структурой молекулы фуллерена 060 и минимальным количеством самопересечений. На рис. 4.2 видно, что каждое кольцо принимает свернутую (двухслойную) форму и окружено пятью другими кольцами, все кольца трансформированы в двухслойные пятиугольники. Если пренебречь наличием вершин степени два, а слои двуслойных пятиугольников (колец) максимально прижать друг другу, то граф образует классическую форму фуллерена 060 (рис. 4.3).

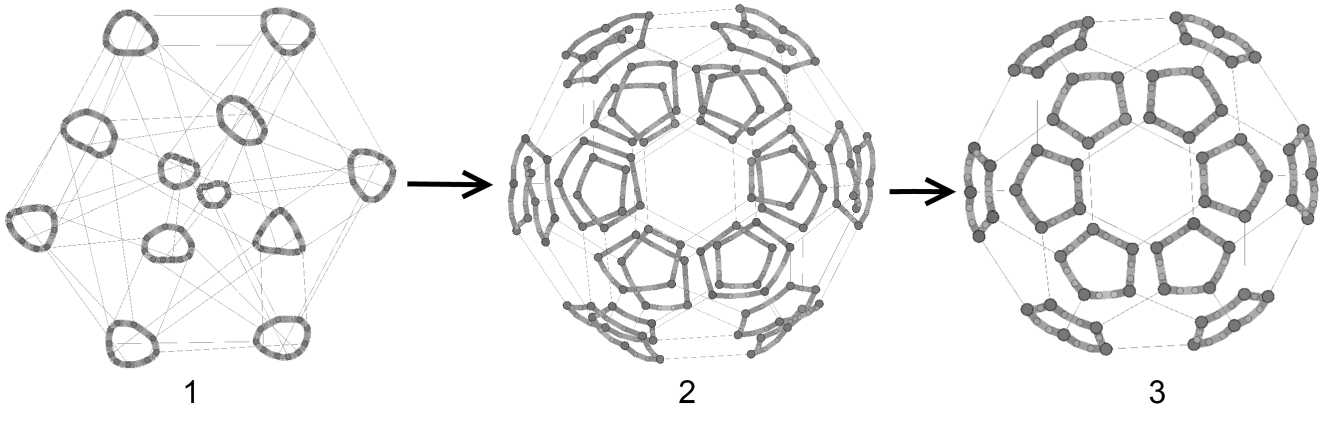
Рис. 4. Различные представления графа S.

Подобная организация графа, через двуслойную структуры колец, объясняется повторным чередованием смежных колец. В распечатке списка вершин кольца S¹ (рис. 5) знаком «>>» помечены десять вершин третьей степени, латинская цифра указывает на номер кольца, в которое можно перейти из данной вершины, а рисунки 3 и 6 показывают трансформацию кольца с 30 вершинами в свернутую, двуслойную структуру. Видно, что первые 5 вершин степени 3 верхнего слоя (рис. 5-6), соединяются с одинаковыми смежными кольцами в том же порядке, что и оставшиеся 5 вершин второго слоя, данная закономерность отслеживается во всех 12 кольцах.

[0, 1, 2, 3, 4, 5]	[3,	4,	5,	0,	1,	2]
1: [1, 0, 2, 3, 4, 5]>> II	6:   [3,	4,	5,	1,	0,	2]>> II
[1, 2, 0, 3, 4, 5]	[3,	4,	5,	1,	2,	0]
[1, 2, 3, 0, 4, 5]	[0,	4,	5,	1,	2,	3]
2: [1, 2, 3, 4, 0, 5]>> III	7:   [4,	0,	5,	1,	2,	3]>> III
[1, 2, 3, 4, 5, 0]	[4,	5,	0,	1,	2,	3]
[0, 2, 3, 4, 5, 1]	[4,	5,	1,	0,	2,	3]
3: [2, 0, 3, 4, 5, 1]>> IV	8:   [4,	5,	1,	2,	0,	3]>> IV
[2, 3, 0, 4, 5, 1]	[4,	5,	1,	2,	3,	0]
[2, 3, 4, 0, 5, 1]	[0,	5,	1,	2,	3,	4]
4: [2, 3, 4, 5, 0, 1]>> V	9:   [5,	0,	1,	2,	3,	4]>> V
[2, 3, 4, 5, 1, 0]	[5,	1,	0,	2,	3,	4]
[0, 3, 4, 5, 1, 2]	[5,	1,	2,	0,	3,	4]
5: [3, 0, 4, 5, 1, 2]>> VI	10: [5,	1,	2,	3,	0,	4]>> VI
[3, 4, 0, 5, 1, 2]	[5,	1,	2,	3,	4,	0]

Рис. 5. Пример списока вершин кольца >5¹ .

Рис. 6. Преобразование кольца S¹ .

Заключение

В результате нашего исследования пазла 2x3 с точки зрения теории автоматов был получен граф, который по своему строению оказался очень похож на структуру фуллерена С60, только в данном случае вместо 60 элементов соединение состоит из 360 вершин, из которых 120 вершины третьей степени и 240 вершин второй степени. Следует отметить так же, что в природе структуры состоящие из вложенных друг в друга концентрических сфер, состоящие из атомов углерода, известны как углерод луковичные структуры или углеродные нанолуковицы. Возможно, из-за особенности строения в два слоя, с двумя видами входящих в ее структуру узлов из 360 элементов, есть вероятность получения нового вида материала.