Автомодельные и неавтомодельные турбулентные течения вязкого газа в коническом диффузоре

Известно, что для стационарного ламинарного течения несжимаемой жидкости от источника, расположенного в вершине конического диффузора, в отличие от известного течения Гамеля между двумя плоскими стенками, наклоненными друг к другу под углом, не удается построить автомодельное решение задачи [1]. Любопытно, что для аналогичного течения вязкого сжимаемого газа, при определенных условиях автомодельное решение существует, что впервые было показано в работах [2-5]. В [2] решена задача об истечении газа, из осесимметричного источника, в канале с граничными условиями проскальзывания и температурного скачка, на. поверхности конуса. В [3-5] решена, аналогичная задача, с от-водом/притоком массы на. стенках канала, с заданной температурой.

В работах [6-10] проведено более широкое и полное исследование рассматриваемой проблемы. В частности, получены аналитические и численные решения автомодельной задачи для ламинарного течения вязкого газа, в каналах с непроницаемыми стенками. Когда, температура. газа, постоянна, вдоль линий тока, а. коэффициенты переноса, являются степенными функциями температуры, в [6] построены аналитические решения, а. в [10] аналогичные

решения впервые получены для плоской ламинарной струи, вытекающей из линейного источника импульса. В работах [7,8] исследована автомодельная задача об осесимметричном течении газа в конусе.

В недавно опубликованной статье [11] для течения в бесконечном конусе впервые установлена возможность построения автомодельных турбулентных режимов течения. Оказалось, что в рамках классической гипотезы Буссинеска и модели Прандтля для турбулентной вязкости уравнения турбулентного движения, записанные в сферических координатах, допускают разделение переменных. В этом случае определяющую систему уравнений Навье-Стокса, осредненных по Фавру, удается свести к системе обыкновенных дифференциальных уравнений.

Заметим, что все полученные автомодельные решения описывают реальные течения, которые возникают в конечной области размером D, если источник массы либо импульса бьет не из точки, а из конечной области d ^ D. При этом автомодельное решение оказывается справедливым на расстояниях А, много больших d и вместе с тем много меньших D. В работе [9] с помощью прямого численного моделирования уравнений Навье-Стокса изучены неавтмодельные режимы ламинарного течения в коническом диффузоре конечной длины и определены расстояния, на которых реализуется автомодельный режим. Однако надо иметь в виду, что в действительности течение от достаточно сильного источника является турбулентным.

В настоящей работе численно изучается процесс выхода неавтомодельных турбулентных режимов течения в диффузоре конечной длины на автомодельный режим в рамках двух популярных моделей турбулентности.

2.    Автомодельные турбулентные течения в конусе

Схема рассматриваемого стационарного течения внутри конического диффузора представлена на рис. 1. Источник газа расположен в вершине конуса с полууглом раствора а.

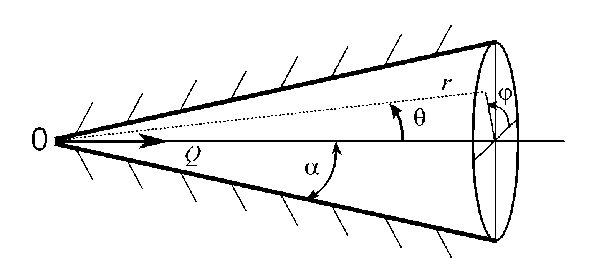
Рис. 1. Схема, течения вязкого газа, в коническом диффузоре

Уравнения Навье-Стока для турбулентного течения вязкого сжимаемого газа, осред-ненные по Фавру, записанные в сферических координатах ( г, Ө, у), имеют вид [14]:

Эн

рпа7 =

-

+       (г2(ст„. + СҒГтт)) + дг г2 дг

+

г

1 а

^-Ө + ^ГгӨ ) sin Ө) [ sin Ө оӨ

-

^ӨӨ

-

^ГӨӨ

-

^рр

-

^Грр^ ,

-1 S+4 !г тмө+оттө)) +(3)

Г дӨ   Г3 дт'

⁺ Г [дӨ ^(<Іөө ^{+ а}төө ) ^{+ (а}өө ^{+ а}төө - o_w ^- сттфф) ctg ^ө] = О,

_ ds 1 д           дТ\     1 ддТ рТиТт = Г2 дГ ((к + Кт)т дт) + ГШПё до ((к + ктөәө)+(4)

7 + 77 ₂     2      2    2-2 1   2            1 д     ₂ ди \ \²

⁺    2    Кг^{+ е}өө^{+ e} _w ^{+ 2е}ге\ ^- з^(?7 ⁺ w ) (^т 2 эГуэГ)) "

Здесь р, Т, р, S — соответственно плотность, давление, температура и энтропия единицы массы; течение предполагается радиальным: V = (и, 0, 0). Газ считается совершенным с уравнением состояния р = pRT, а коэффициенты вязкости 7 и теплопроводности к зависят от температуры по степенному закону.

Отметим, что по сравнению с уравнениями Навье-Стокса для ламинарного течения в уравнения (1) - (4), помимо членов с ламинарным тепловым потоком и вязкими напряжениями, входят дополнительные члены с турбулентными напряжениями и турбулентным тепловым потоком.

Компоненты тензора вязких напряжений ст определяются следующими соотношениями:

27 д ст?? = 7ЕТТ - — —

3т ² дт

2 ди\                и 27 д

(^т .-     ' = ' ■■ = ²⁷ Г ^- зГ 2 дГ

(^Г2 5г)

;ст_гө = ЧЕгө,

ди

Е = 2    : Еөө дт

= E_W = 2 — ;Е _ге = 1 £. т т дт

Тензор турбулентных напряжений стт и турбулентный тепловой поток qт, согласно гипотезе Буссинеска [12,13], представляются в виде сттгг = 7тЕтт - I7! к Г2д |и) ; сттөө = сттфф = 27ти - I7! 1" ГТ'2 Д") ; сттгө = 7тЕгө,

3т2 дт \ дт                      т 3т2 дт \ дт q-T = -к^Т.

В соответствии с теорией пути смешения Прандтля коэффициент турбулентной вязкости 7_т определяется по формуле [14,15]:

Р^ ²

7т = — т

ди дю

где I — длина пути смешения. Турбулентный коэ<1 я Циппеит теплопроводности кт связан с 7т известным соотношением:

7т с_Р Кт         .

¹    Рг _т

Число Прандтля Рг в одноатомном газе близко к 2/3, а турбулентное число Ргт для простоты принято равным единице Ргт = 1 [14].

Для вывода автомодельной системы уравнений газодинамические переменные представлены в следующем виде [11]:

и(Ө)      р(О)       _m__{2 m}   Т (Ө)      /Т(Ө) ^k          7

^и = "^Т,р = Г ^+2 ,Р = ^т   Р^(Ө),^Т = _Г2^,7 = (ф2^) ,^к = _Рг(1 - ₇) 7.

В формуле (5) присутствует длина пути смешения Прандтля I, которая в осесимметричном случае определяется как

I = Xr(a - 0), где X — некоторый постоянный коэффициент, значение которого находится с использованием экспериментальных данных. Окончательно выражение (5) можно переписать в виде

Рт = ¹ р(0)х² (а — 0)2 г

dn d0

Оценивая порядок правой части уравнения (6), находим, что рт ~ 1/г. С учетом порядка вязких «ламинарных» и «турбулентных» членов, входящих в (1) - (4), с учетом полученной оценки для рт, находим следующий критерий автомодельности течения:

2mk = 1,

Таким образом, система определяющих уравнений в частных производных сводится к нелинейной системе обыкновенных дифференциальных уравнений (7) - (9):

^(ткdn sin 0) + 4(m2 - 1)nTkl +(7)

Re0 [sin0 d0 \ d0 /   3VJ

+X2 [-1У   f(a - 0)2Р^ ^ sin0) + 4(т2 - 1)(а - 0)2P sin 0 d0 \         d0 d0 )   3d0

+(m + 2)p + mpn² = 0,

dp d0 =

+X2 [(1 — m)(a - 0)2p

R50 [(1 — m)Tk+ 3(1+ m)dTУ] + dn dn 2 . x d A „.9 dn \ 1 d0 d0 + 3(1 + m)d0 ((а - 0) p d0 <#

pn (2 - m⁷-^-⁴) =---------- [4m² T1^+k +        (t ^{k IT} sin 0) 1 +

\     7 - 1/   PrM0(7 - 1)Reo [           sin 0 d0 \ d0 /]

+

X2

РгтM2 (7 - 1)

[4m² T(a - 0)2

dn

P d0

+   6а - 0)2P d0 \

dn dT Al

Тө Те^{sin ө}) ] ⁺

+4(m + 1)2“2 + f55)  + X2(“ - 0)2P ^  4(m + 1)2n2+ f^)

Reo  3              \dd J                 d0  3              \ d0)

с краевыми условиями на оси:

при 0 = 0,

(Ю)

(И)

ⁿ = Р = 1, ^т = Р = П12 , 7^M0

и на поверхности конического диффузора в случае заданной температуры:

n = 0, T = Т,_ш, при 0 = а.

В работе [11] краевая задача (7) - (11) была решена численно для течения газа твердых сфер, то есть при m = 1 и к = 1/2. Оказалось, что аналогично ламинарному случаю, автомодельное турбулентное течение существует только в ограниченном диапазоне определяющих параметров. Максимально возможный полуугол раствора а*, при котором решение существует, составляет примерно 60°. Для турбулентного течения в отличие от ламинарного при а ^ 0 решение перестает существовать. Как было установлено в работе [11], максимально возможное значение числа Маха на оси достигается при а* га 5.7 и равно М0 га 1.9.

Исследование автомодельного турбулентного режима течения также показало, что физически приемлемые результаты, как и в «ламинарном» случае, имеют место только для конусов с небольшим полууглом раствора а, когда не нарушается условие сплошной среды, т.е., при числах Кнудсена Kn = M/Re ^ 1.

3.    Неавтомодельные турбулентные течения в коническом диффузоре

Для численного моделирования неавтомодельных турбулентных режимов рассмотрим течение вязкого газа в усеченном коническом диффузоре конечной длины. Схема течения представлена на рис. 2.

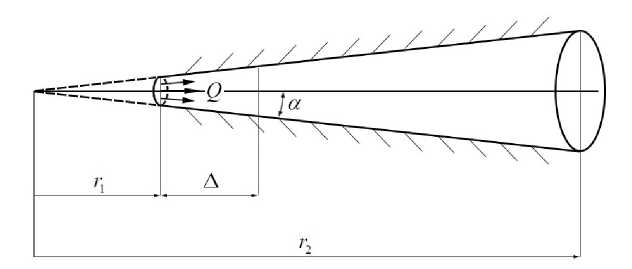
Рис. 2. Схема, течения вязкого газа, в усеченном коническом диффузоре

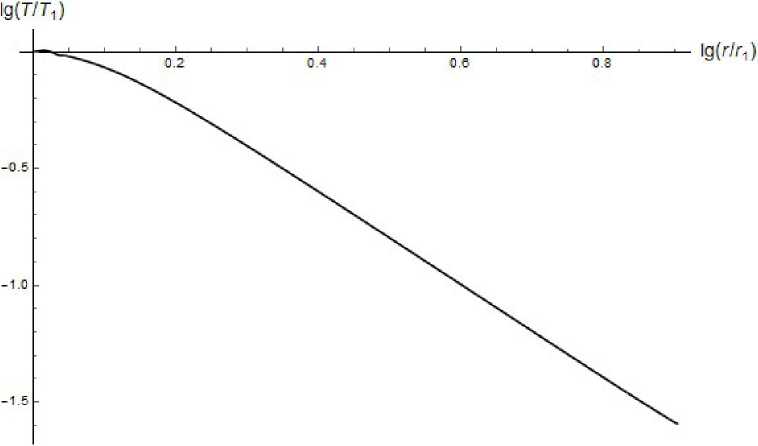
Рис. 3. Распределение температуры па. оси конического диффузора.

Для практических расчетов были выбраны следующие геометрические размеры конуса: щ = 0.03 м, 7*2 = 0.24 м, полуугол раствора а = 0.05 рад га 2.90 и параметры течения: на входной границе при r = ri скор ость ni = 972 м/с, температура Т1 = 273 К. Температура на стенке задавалась по степенному закону [11]: Тш = 273 • (т/тД2, г де r — расстояние от вершины конуса. Такой закон распределения температуры на границе соответствует автомодельному решению, где Т = Т(Ө)/т2. На выходной границе ставилось условие для давления: р2 га 0.7 Па. Расчет проводился для одноатомного гелия. Ниже приведены ре- зультаты расчетов с использованием двухпараметрической к — е модели турбулентности для замыкания системы уравнений.

На рис. 3 в логарифмических координатах показано распределение температуры на оси усеченного конического диффузора.

На участке г Е [(гі + А), г2] логарифм температуры линейно зависит от логарифма радиальной координаты г, то есть решение выходит на автомодельный режим на расстоянии А ~ 0 . 02 м от входного отверстия, при этом: А ~ 0 . 02 м ^ a • гі ~ 0 . 0015 м. На участке г Е [(гі + А), Г2] для температуры выполняется следующая степенная зависимость: Т ~ г-1. 98, что хорошо согласуется с автомодельным решением Т ~ г². Таким образом, решение выходит на автомодельный режим на расстоянии много большего размера входного отверстия, о чем было сказано во введении.

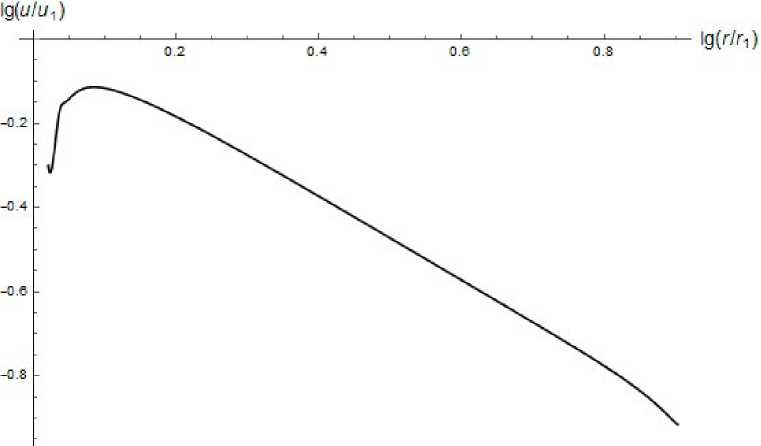
Рис. 4. Распределение скорости на оси конического диффузора.

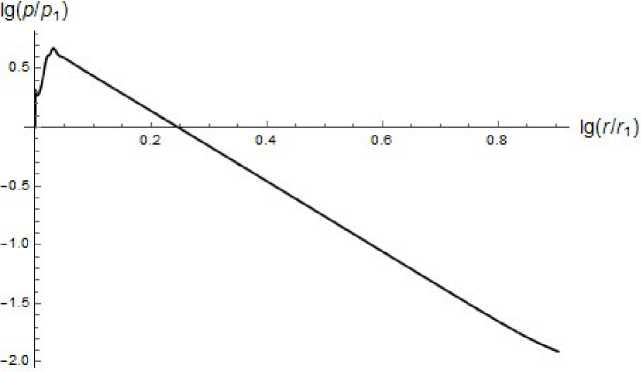
Рис. 5. Распределение давления на. оси конического диффузора.

Распределение скорости на. оси конуса, представлено на. рис. 4. Для скорости степенная зависимость практически такая же, как и у автомодельного решения: п ~ г^-1. При этом на участке г Е [гі, (гі + А)] амплитуда скорости плавно возрастает до некоторого максимального значения, после чего убывает по степенному закону.

Распределение давления представлено на. рис. 5. Как видно из представленной зависимости логарифма давления от логарифма координаты г, выполняется следующая степей- ная зависимость: р ~ г и ~ г 3.

2.96, что является достаточно близким к автомодельному решению:

Наибольший интерес представляет проверка, степенной зависимости для коэффициентов турбулентной вязкости и теплопроводности. На рис. 6 представлена, зависимость турбулентного коэффициента, теплопроводности на. оси конуса. Степенная зависимость имеет вид: «г ~ _г-0.99

Коэффициент турбулентной вязкости имеет такую же степенную зависимость на оси конуса, что и коэффициент теплопроводности, как следует из распределения Ргт, которое показано на. рис. 7. Полученный результат хорошо согласуется с формулой (6), которая используется в турбулентной модели пути смешения Прандтля.

Отметим, что автомодельное решение удается найти только для специальной комбинации определяющих параметров задачи ( Reo, Мо, а) и граничного условия для температуры на стенке в форме: T_w ~ 1]т2. Указанные комбинации найдены в работе [11].

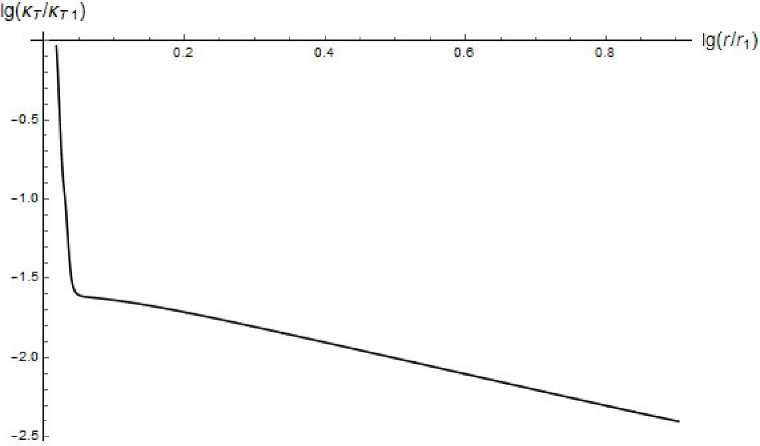
Рис. 6. Распределение турбулентного коэффициента, теплопроводности на. оси конического диффузора.

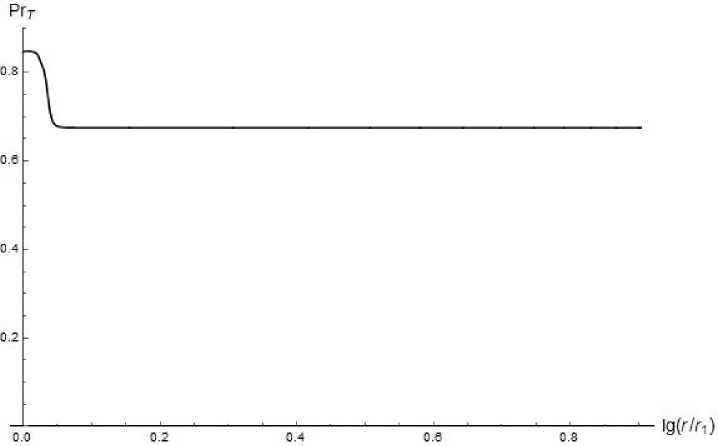
Рис. 7. Распределение турбулентного числа. Прандтля на. оси конического диффузора.

4.    Заключение

Проведен численный анализ задачи о турбулентном течении вязкого газа в усеченном коническом диффузоре. Полученные в ходе численного моделирования результаты сравнивается с аналогичным автомодельным решением для бесконечного конуса. Установлено, что автомодельное решение существует только для определенной комбинации определяющих параметров задачи и специальных граничных условий, а количественная зависимость от координаты г турбулентных коэффициентов переноса соответствует основному предположению турбулентной модели пути смешения Прандтля, записанной для осесимметричного случая в форме (6).

Показано, что турбулентное течение выходит на автомодельный режим на расстоянии А от входной границы, которое значительно больше размера d = a • гі входного отверстия, из которого истекает газ, но значительно меньше размера области течения D = Г2 — гі.