Автореверсивная втулка из материала с ЭПФ для прецизионного шлифования тонкостенных осесимметричных деталей

Простым и надежным решением данной задачи является применение материала с эффектом памяти формы (ЭПФ) для изготовления рабочей части шлифовальной оправки в виде втулки. Втулка, изготовленная из сплава, обладающего ЭПФ (например, TiNi ), после соответствующей предварительной термосиловой подготовки, способна уменьшаться в диаметре при нагреве (этап установки заготовки) и увеличиваться при охлаждении (этап закрепления и обработки). Свойства сплавов с ЭПФ позволяют обеспечить требуемую стабильность и осесимметричность радиальных перемещений [1].

Для реализации данного подхода необходимо внешнее силовое воздействие, обеспечивающее раздачу самой втулки при температурной разгрузке – охлаждении. В подобных случаях, для силового элемента с ЭПФ в виде кольца или полого цилиндра малой скважности, решением служит дополнительный упругий элемент, например реверсивная пружина. В рассматриваемом случае, при большой скважности, использование реверсивной пружины является проблематичным. При проведении предварительных экспериментов с силовым элементом данного вида, обнаружен эффект автореверсивного ЭПФ, возникающий и стабильно воспроизводящийся при определенном соотношении геометрических параметров и условий термосиловой подготовки силового элемента рассматриваемого типа. Данный эффект возникает, если в процессе предварительной принудительной раздачи втулки в псевдопластичной фазе деформация внутреннего слоя превышает предел текучести её материала. Тогда при восстановлении исходной формы в процессе фазового перехода (при автообжиме) в этой области наводятся сжимающие напряжения, препятствующие деформации восстановления.

Для успешного практического применения предложенного процесса прецизионного шлифования требуется создание методики проектирования станочных приспособлений с силовым элементом из сплава с ЭПФ в форме втулки с заданным диапазоном изменения диаметра рабочей поверхности в зависимости от номенклатуры сечений и материала обрабатываемых деталей. Для создания данной методики необходима разработка математической модели термосилового взаимодействия силового элемента из сплава с ЭПФ в форме втулки с обрабатываемыми деталями, позволяющая управлять напряженно – деформированным состоянием системы деталь-приспособление.

Характер закрепления при нагружении заготовки в процессе её обработки дает основание принять в качестве допущения возможность рассматривать ее как оболочку при плоском напряженно-деформированном состоянии. В этом случае, как известно [2, 3] состояние осесимметричного объекта под внутренним давлением определяется тангенциальной компонентой напряжения и средним радиусом кривизны оболочки по уравнению Лапласа:

— R

E

С1

V

^^^е

У

— = p

R h,

Величина крутящего момента, передаваемого оправкой через втулку с ЭПФ на заготовку в процессе шлифования, при значительной площади контакта достаточна при минимальном контактном давлении. Задавшись для гарантирования чисто упругой раздачи заготовки величиной — = 0.5 — ₀ 2 , определяем необходимую величину рабочего хода втулки из материала с ЭПФ с помощью выражения (2).

Исходными соотношениями феноменологической модели силового элемента, форма которого, как и заготовка, имеет вид втулки, принимаются схематизированные экспериментальные зависимости, представленные на рис. 1 [4]:

По граничным условиям силового элемента с ЭПФ в процессе предварительного деформирования при его термосиловой подготовке и последующего функционирования допускаем, что он находится в плоскодеформированном состоянии - e z = 0 . Ввиду малости последней по сравнению со средней величиной остальных компонент деформаций примем условие несжимаемости (квазипластическе состояние):

^е р + ^е ф = ⁰ , (3)

где — - тангенциальные напряжения; R - средний радиус оболочки; p – давление на поверхности контакта с оправкой; h – толщина стенки. Раздача детали под давлением p и опоясываю- p щим растяжением — = R определяется согласно [2]:                 h

где е_р , е_ф - радиальная и окружная компоненты тензора деформаций.

Объединяя (3) и уравнение совместности деформации, имеющее в рассматриваемом случае вид [2]:

e ev - ep_n = 0

d p    р

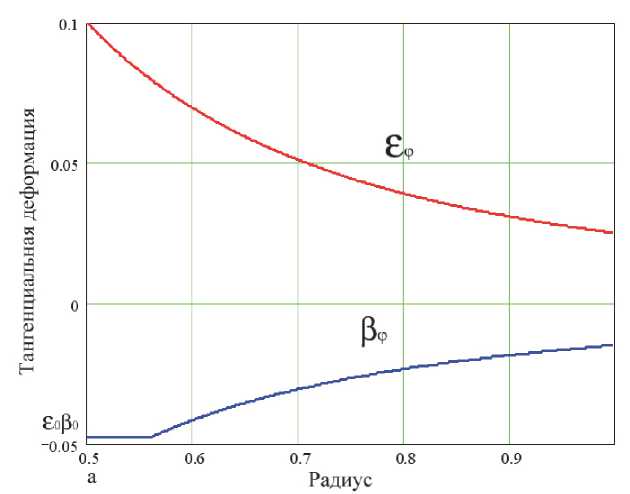
Рис. 1. Распределение тангенциальных деформаций наведения e_j и тангенциальной структурной деформации b_j по радиусу силового элемента с ЭПФ в виде втулки

получаем интеграл в тангенциальных деформациях вида

a

^£ _Ф = р А ,              (5)

где а - внутренний диаметр распорной втулки; 2 А - величина ее раздачи по внутреннему диаметру; р - радиальная координата.

При моделировании процесса переклистал- лизационного возврата геометрии силового элемента при его функционировании введем допущение, что температурное поле равномерно по его сечению (безградиентное) вследствие невысокой скорости нагрева или охлаждения системы деталь-приспособление. Пусть a и b - соответственно внутренний и наружный радиус втулки с ЭПФ. Также примем следующие допущения:

• 1)    напряжения в материале силового элемента в процессе функционирования ограничены пределом упругости высокотемпературной фазы (соответствующей температуре конца обратного мартенситного превращения материала силового элемента);

• 2)    материал втулки по-прежнему находится в плоскодеформированном состоянии: £ z = 0 ;

• 3)    тензор структурно-фазовой деформации является ортотропным девиатором и связан с начальной деформацией (деформацией наведения) согласно рис. 1.

В таком случае приходим к системе уравнений, аналогичной осесимметричной краевой задаче термоупругости для полого цилиндра с закреплёнными торцами, содержащей: обобщённый закон Гука в цилиндрической системе координат

£ + Р = ^ [(1- мН - Мнр ]

1 E                  (6)

^р - Р = 4г[(1-мН- му ];

E уравнение равновесия dap

У = у+р   ;(7)

v р уравнение совместности деформации d£„

£р = £Ф + Рг" .(8)

р v

Величины E и р - соответственно модуль Юнга и коэффициент Пуассона материала силового элемента.

Граничные условия в напряжениях на основании очевидной разгрузки при автообжиме втулки поверхности р = b и отсутствие нагрузок на поверхности р = a можно принять однородными: ^н р ⁽ a ) = ^Н р ⁽ b ) = ⁰ .            ⁽⁹⁾

Переходя к нормированной величине на- пряжений <г(р) =

¹ - м²

E

^н р ( Р ) ,

систему (6)-(8)

сводим одному уравнению вида:

d f зda |   d у I р г 1=;гр 2 в).      (10)

d p V   d p) d p

Решая краевую задачу (10), (11) с учетом деформационных зависимостей (5), проиллюстрированных рис. 1, получаем:

^a p = Ц 1 -V

n )

/

2 A

~ a9

= ^{- X 1 +} ^ 2 J ⁺ ' ⁿ )

V

П n, a < n < X a n - +1 f 1 - XT], X < n < 1

• ^a ^ V n )

  n ⁿ + 1, a <  n <  X a

  
  

  ( A

  
  

  X

  
  

n ^X + ¹ 1 + ^ , X <  n < 1 ,(11) a 2²

V

n )

где ñ– граница области предельной деформации при предварительной раздаче; £0 - величина предельной обратимой деформации; р0 - коэффи- р циент обратимости деформации; n = — - безраз-b

~ 1 — р¹

мерная радиальная координата; a = —   a ;

E P o ^£ 0

ac 1

a = T; X = v; ^ = ;--- b b 1 — a n X+i^^2 a 2

На рис. 2 показано распределение напряжений, определяемое с помощью выражения (11).

Как видно из (11) и рис. 2, во внутренних слоях втулки наводятся значительные по величине сжимающие тангенциальные напряжения, способствующие возвращению геометрических параметров данной втулки с ЭПФ, в исходное состояние.

Если сделать допущение, что в процессе прямого мартенситного превращения, при охлаждении реального силового элемента с ЭПФ, из - за градиента температурного поля, граница перекристаллизации перемещается от внешней поверхности рассматриваемого силового элемента к его внутренней поверхности (что происходит при установке холодной заготовки на нагретую втулку, а также и при конвективном теплообмене на наружной поверхности нагретого силового элемента), эти сжимающие тангенциальные напряжения, предположительно, возрастут и более эффективно выполнят функцию возвратной пружины, способствуя стабильной автореверсив-ной работе втулки и, тем самым, дополнительно обеспечат надежную многоцикловую фиксацию заготовок. При этом величина автораздачи вследствие слабой сопротивляемости внешних слоев, переходящих в квазипластическое состояние в

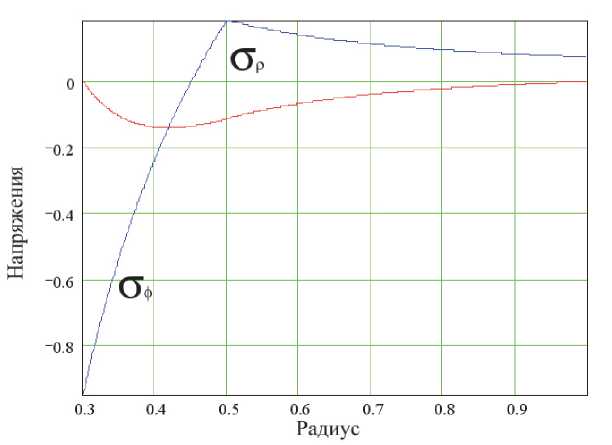
Рис. 2. Распределение тангенциальных напряжений s_j и радиальных напряжений s_r по радиусу силового элемента с ЭПФ в виде втулки с радиусом 1 при относительном к радиусу внешней поверхности значении радиуса текучести 0.5 и при соотношении структурной деформации и деформации наведения 0.6

«мягкой» (мартенситной) фазе, практически равна величине начальной принудительной раздачи, и составляет на внешней поверхности

a w= w, (12) b где w – величина начальной раздачи по внутренней поверхности, определяемая согласно (2) и (5). Высказанное допущение требует дальнейшей теоретической и экспериментальной проверки.

Таким образом, результаты математического моделирования процесса функционирования силового элемента в виде втулки из материала с ЭПФ, входящего в конструкцию оправки для прецизионного шлифования в рамках феноменологической теории деформируемого твёрдого тела позволяют сформулировать наиболее простое объяснение механизма экспериментально наблюдаемого автореверсивного режима и подтверждают возможность его практического использования.

Дальнейшее развитие полученных результатов предполагается получить путём детализации модели за счёт выявления зависимости величины рабочего хода и натяга втулки из материала с ЭПФ оправки для шлифования от её геометрических параметров и параметров термосиловой подготовки, а также за счёт учета неравномерности температурного поля, которая существует при функционировании реального силового элемента из сплава с ЭПФ. Детализированная математическая модель функционирования силового элемента приспособления для прецизионного шлифования, после всесторонней экспериментальной проверки, может быть использована для разработки методики проектирования данных приспособлений и позволит охватить достаточно широкую номенклатуру тонкостенных деталей, для которых необходимо прецизионное шлифование.