Bank Customer Credit Scoring by Using Fuzzy Expert System

Published Online October 2014 in MECS

One of the most important economical developments of each country is based on its investments. Banks and credit institutes as financial inductors allocated a significant portion of the financial markets in the supplying invested capitals. Also credit facilities are an important part of banking resources. Banks accept the requests of applicant provided that ensure the applicant could refund the credit.

While the banking system being faced impressive growth of expired payments. So the most important problem in banking affairs is investigating and decisionmaking about granting facilities.

In contemporary banking systems, traditional decision making methods have been excluded and intelligent systems are often used [1]. Increasing accuracy, omitting personal judgments and decreasing decision making time are the advantages of such systems. They are trained by learning samples (previous confirmed or rejected requests) and then trained system is used in new situations [2]. Therefore a system is required that could consider all data in a short time, check the situation of granting facilities and if it’s possible generate corresponding rules used by experts. Because this system is obtained based on previous applicants information, performs similarly for different applicant in the same situations; unlike other personal decision-making methods which are changed by personal opinions. In addition, since banks tries preventing the risk of no fundable credits, intelligent systems could recognize the credit with high probability of default [1,3].

Such system could be one of the Artificial Intelligence methods like fuzzy expert system which uses predefined membership functions for fuzzy features and fuzzy inference rules to map numeric data into linguistic variable terms and to make fuzzy decisions [4,5].

The rest of paper is organized as follows: next section is related work. Methodology is described in section III. In section IV the empirical study is shown. Evaluation and results are given in section V. Paper is concluded in section VI.

• II.    R ELATED W ORKS

Already many researches have been done to design the intelligent decision-making systems for credit scoring problem. The output of these algorithms are models generated based on the input information with high accuracy. Input data includes the type of facility (loan), amount and number of loans, type of repayment, applicants' income, the number and value of guarantee and etc. Finally, the proposed model divides applicants into groups [3]. So credit scoring is a typical data mining (DM) classification problem which decided an applicant is a good or bad one for refunding the facility.

In [6] a fuzzy approach for credit rating of a bank's customers in Taiwan was studied. In this approach, the rules were used based on expert knowledge. The generated fuzzy rules lose their effectiveness, because different experts produce different rules and also with the change of the rules of this field.

Support vector machine (SVM) and least square error technique were another methods which were used in [7] for credit scoring. SVM is a well-known solver for classification problem especially when data divided into two groups. The most important disadvantage of this model is that it’s not interpretable and the expert couldn't understand why such an output is determined.

Also [8] was studied, which used neural networks and genetic algorithm to classify customers into two groups, "good" and "bad". These methods like the previous method have high computational complexity and also because of the stochastic computation, has no the fixed precision in its decision also there is no obtained rule to help users why such a decision is made.

In [9] an integrated data mining and behavioral scoring model was used as a classification method, to manage existing credit card customers in a bank. A SelfOrganizing Map (SOM) neural network was used to identify groups of customers based on repayment behavior and frequency, monetary behavioral scoring predicators. It classified bank customers into three major groups of customers. The proposed method was tested on bank databases were provided by a Taiwanese credit card issuer. This system is also a black box method that there is no inference rule obtained.

A genetic programming method was also used in [10] for credit scoring in Egyptian public sector banks and the results of the model were compared with probit analysis (an alternative to logistic regression) and weight of evidence measure. Two evaluation criteria used in the modeling were average correct classification and estimated misclassification cost. Genetic programming is a type of stochastic process and like all other methods in this group the answer of such system could be changed during different usages.

Several methods like neural network, support vector machine and evolutionary algorithms are used as the soft computing methods to resolve the credit scoring problem in [11]. Neural networks and support vector machine do like a black box and don't explain anything about the reasons of making-decision to the users. Also evolutionary algorithms have a stochastic process which there is no insurance to reach the same answer in several executions.

The combination of support vector machine and four different methods like decision tree, linear discriminant analysis, rough sets and F-score, are used to credit rating in [12]. The accuracy of this model was rather high but high complexity of computation is the most noticeable problem in this combination and this method is very time consuming.

In [13] a model was obtained for credit rating by using logistic regression for a bank in Iran. This paper used information of 310 people to determine the main factors in credit risk. This data is used to find the performance of the model. The disadvantage of this model is the complexity of computation which is very high.

Two dual strategy ensemble trees are introduced to classify credit scoring in [14]. RS-Bagging DT and Bagging-RS DT, which are based on two ensemble strategies: Bagging and random subspace, to reduce the influences of the noise data and the redundant attributes of data and to get the relatively higher classification accuracy. In addition several other methods are used to compare the results like Multi Layer Perceptron (MLP),

Logistic Regression Analysis (LRA), and Linear Discriminant Analysis (LDA).

In [15] the credit scoring of one of the Iranian bank has been studied and Logistic Regression Analysis (LRA), and Linear Discriminant Analysis (LDA) methods are used to predict the credit scoring of banking customers. The data used in this article includes the information of banking customers from 2006 to 2011. The results show that LRA method has better performance for this dataset.

Two Credit Scoring Models (CSMs) for the Sudanese banks were studied in [16]. These methods are based on data mining classification techniques, Decision Tree (DT) and Artificial Neural Networks (ANN). In addition Genetic Algorithms (GA) and Principal Component Analysis (PCA) are also applied as feature selection techniques to decrease the complexity of problem and find the most effective features.

In [17] a fuzzy expert system was proposed to classify bank customers for granting banking facility. The model was generated based on the data collected from one of the Iranian Bank (information of more than 2000 bank customers). Result shown the good performance of the model.

• III.    M ETHODOLOGY

Since credit scoring is a decision-making problem, expert systems could be used to solve it. Fuzzy expert systems can be seen as special rule-based systems that use fuzzy logic. A fuzzy rule-based expert system contains fuzzy rules in its knowledge base and derives conclusions from the user inputs and the fuzzy reasoning process.

Fuzzy set theory have been developed to manage uncertainty and noise. because of its simplicity and similarity to human reasoning, fuzzy set theory is frequently used in expert systems. Fuzzy set theory was first proposed by Zadeh in 1965 and was concerned with reasoning using natural language in which many words have ambiguous meanings [18].

Fig. 1 shows the artchitecture of a fuzzy expert system.

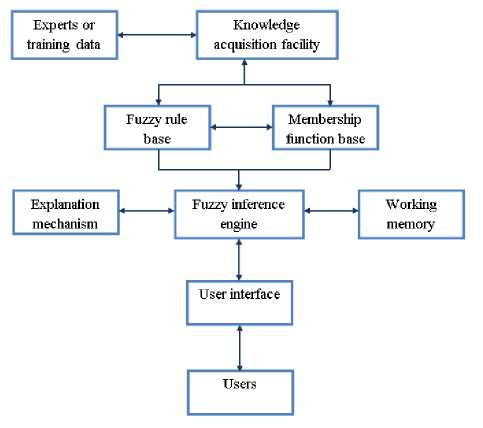
Fig. 1. Architecture of fuzzy expert system[4].

Fuzzy expert system includes:

• •    User interface : for communication between users and system.

• •    Membership function base : a mechanism that presents the membership functions of linguistic variable terms.

• •    Fuzzy rule base : a mechanism for storing fuzzy rules (expert knowledge).

• •    Fuzzy inference engine : executable program includes fuzzy matching, fuzzy conflict resolution and fuzzy rule firing.

• •    Explanation mechanism : a mechanism that explain the inference process.

• •    Working memory : a storage to save inputs and temporary results.

• •    Knowledge acquisition facility : an effective machinelearning approach to deriving rules and membership functions automatically from training instances [4].

The way that a set of fuzzy rule is generated is illustrated in the rest of this section.

• A.    Rule extraction and representation of knowledge by the fuzzy “if-then” rules

Fuzzy logic formulates linguistic rules for fuzzy models so that can be easily understood by experts. While, all mathematical details are concealed. The rules of such system are in the form of fuzzy if – then, like:

if x isA andx isA x isA ThenyisB

• •    Phase 1 : divide the input and output space into fuzzy region.

• •    Phase 2 : generate fuzzy rules from given data pairs.

• •    Phase 3 : assign a degree to each rule.

• •    Phase 4 : create a combined fuzzy rule base.

• •    Phase 5 : determine a mapping based on the combined fuzzy rule base.

• B.    From crisp to fuzzy sets

Let U be a collection of objects u which can be discrete or continuous. U is called the universe of discourse and u represents an element of U . A classical (crisp) subset C in a universe U can be denoted in several ways like, in the discrete case, by enumeration of its elements: C = (ц,u2,....,up} with V/: u, e u . Another way to denote C (both in the discrete and the continuous case) is by using the characteristic function XF : U ^ (0,1} according to XF (u) = 1 if u e C , and XF(u) = 0 if u £ C . The latter type of definition can be generalized in order to define fuzzy sets. A fuzzy set F in a universe of discourse U is characterized by a membership function µ Which takes values in the interval [0,1] namely, pF : U ^ [0,1].

• C.    Operators on fuzzy sets

Let A and B be two fuzzy sets in U with membership functions µ and µ , respectively. The fuzzy set resulting from operations of union, intersection, etc. Of fuzzy sets are defined using their membership functions. Generally, several choices are possible:

• •    Union : The membership function p_AuB of the union A ∪ B can be defined by:

Vu P a и в = max p ( u ), P b ( u )} or by

^{V u :} P a и в = P a ^{( u} ) + ^р в ^{( u} ) ^— P a ^{( u ) р} в ^{( u} )

• •    Intersection : The membership function p_AnS of the union for all A ∩ B can be defined by:

Vu P a _n в = min p ( u ), P b ( u )} or by

^{V u : p} A П B = ^P A ^{(u) p} B ^{( u} )

• •    Complement : The membership function of the complementary fu zzy set A^C Of A is usually defined by

Vu : P a c = 1 — P a ( u )

• D.    Linguistic variables

Modeling of expert knowledge could be done by fuzzy logic. The key notion is that of a linguistic variable (instead of a quantitative variable) which takes linguistic values (instead of numerical ones). Seven levels are considered for each linguistic variable. In other words the value of the linguistic variable can be an interval of its range. Therefore each level has a sub function which shown the degree of dependency of each value to this level.

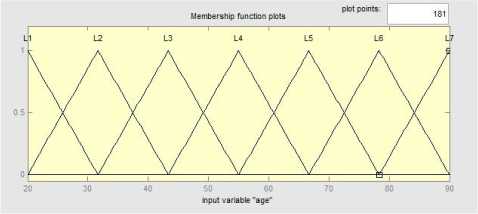
Fig. 2. Example of linguistic variable for a feature

For each linguistic variable boundary of class will be fuzzy. Therefore, these linguistic values are characterized by fuzzy sets described by a membership function as shown in Fig. 2 designed by Matlab. Each level has a triangular membership function (trimf) that is shown in figure by its name. In this figure 7 levels are considered to find best answer for credit scoring problem. The number of level is depended to the problem and may change in different situation and most of the time it could be found by try and test.

Fig. 3 shows the pseudocode of the generating fuzzy rules. This procedure is received the dataset as the training instances and the number of fuzzy set to form the fuzzy membership function “trimf” and the output of system is a set of fuzzy rules obtained from training dataset. To do this first finds the maximum and minimum value of the fuzzy feature to figure out the corresponding “trimf” membership function. Then for each data in training dataset, the membership degree for a set of fuzzy features is computed and the rule with maximum value is selected. For nonfuzzy features use the same value of feature. The generated rule is added to the rule set. At the end of this procedure all duplicated rules are removed since only one instance of them are required.

The main algorithm of fuzzy expert system is shown in fig 4. In this procedure after dividing dataset into training and test dataset, the rule generation procure is called. The input parameters of this procedure are training dataset and the number of fuzzy set which is set to 7. Then obtained rule set are examined by the test data set to find out the accuracy of the system. The accuracy could be computed by equation (1):

TP accuracy = ———                       (1)

where TP is the number of samples which is classified correctly and FP is the number of incorrect classified samples[20]. The obtained accuracy and the generated rule set are the output of the fuzzy expert system. The set of rule is used to interpret the answer of system to a test sample. And explain why a sample accepted or rejected to get the facility.

FuzzyRuleGeneration ( Dataset , number_of_FuzzySet ) {

% Input: Dataset (number_of_training _data, number_of_features), number of used fuzzysets,

% Output: Set_of_Rules ( a set of generated rules according to dataset)

• 1)    Read Dataset from Input File path;

• 2)    Read number_of_FuzzySet from Input file path;

• 3)    Read the number of each fuzzy feature from Input file path;

• 4)    for each fuzzy feature f

• 5)    find minimum and maximum values of f

• 6)    specify the parameter of fuzzySet function according to the number_of_FuzzySet and the maximum and minimum values of f

• 7)    for each data d in Dataset

• 8)    for each fuzzy feature f

• 9)  sssssfind FuzzySet with maximum membership degree according to the value of f in d

• 10)      for each nonfuzzy feature nf

• 11)    ssssuse the same value of nf in d

• 12)    for each data d in Dataset

• 13)      for each fuzzy feature value vf

• 14)    ssssfind the degree of vf in each FuzzySet

• 15)    ssssselect fuzzySet with the maximum degree

• 16)    ruleSet : add one rule from d to the ruleSet

• 17)    assign a degree to each rule, which is equal to the multiply degree of all fuzzySet

• 18)    for each rule in ruleSet

• 19)    find all rules with the same antecedent of rule

• 20)       select rule with the maximum degree

• 21)       delete all similar rules

}

• Fig. 3. Pseudocode for the proposed fuzzy expert system

Fuzzy expert system (dataset) {

% input: whole dataset

%output: the accuracy of model in percentage

• 1)   Read dataset from input file path;

• 2)    Divide dataset into two groups randomly so that 80% of the data are used as the training sample and the rest of them are used for the test of the generated model.

• 3)    Set the number_of_FuzzySet to 7;

• 4)    Call FuzzyRuleGeneration ( training _ Dataset , number_of_FuzzySet ) and obtained Set_of_Rules ;

• 5)    For each data td in test_dataset

• 6)    Ssss find a rule that match with td

• 7)    Ssss compare the label of class in dataset with the answer of model.

• 8)    Ssss if the results of both are the same the model does correct otherwise does incorrect.

• 9)    Count the total number of correct classified sample.

• 10)    Compute the rate of true classified sample toward all dataset samples. (true classified sample into number of test_dataset) }

Fig. 4. Algorithm of fuzzy expert system

• IV.    E MPERICAL S TUDY

In order to verify the performance of proposed fuzzy expert system, three particular credit scoring datasets were used in this study. Two of them, named Australian and German credit scoring datasets, are available from UCI machine learning repository and have been widely used in credit scoring researches.

The Australian dataset includes 690 credit customer information, 307 good customers and 383 bad customers. The information for each customer contains 6 numerical (real, integer) and 8 categorical attributes.

The German dataset has 1000 instances (700 good customers, 300 bad customers) with 20 attributes (7 continuous, 13 categorical).

All attribute names and values have been changed to meaningless symbols to protect confidentiality of the data in two above datasets.

The other dataset is provided by a local bank in Iran, Ansar Bank, includes the information of 2100 bank customers used the bank facility (1200 good customers, 900 bad customers) this dataset was collected from 2007 to 2013. A summary of the characteristics of above datasets is reported in Table 1.

Table 1. Datasets’ Features

	No. of instances	No. of Good/bad instances	No. of features	No. of fuzzy features
Australian credit	690	307/383	14	6
German credit	1000	700/300	20	7
Iranian credit	2100	1200/900	27	5

Since Australian and German credit scoring datasets are standard, it’s not necessary to do data preparation phase. But about Iranian dataset at first some methods such as data cleaning, data normalization and making required features were done to prepare the dataset. About some features with missing value the majority voting method was chosen[21]. And Principal Component Analysis (PCA) is applied as feature selection techniques.

Before executing rule extracting method, the fuzzy features must be specified then the five phases of rule extraction is done. According to the description in the section (From Crisp to Fuzzy) in Iranian dataset there are only 5 features of fuzzy properties. These features are: age, guarantee value, deposit account, deposit period and average salary. All numerical features in the Australian credit dataset and in the German credit dataset could be considered as fuzzy properties (the names of features are not mentioned in these two dataset). As noted in the linguistic variables part, seven levels were considered for each fuzzy features.

For example, age as a linguistic variable has the range of 21 to 86 year olds (T(age) ∈ U[21,86]), this range is divided into seven level. Each variable in T(age) is characterized by a fuzzy set in the universe of discourse, here, e.g., U = [21, 86]. Table 2 shows the range of each level for linguistic variable age. A list of 7 levels and their intervals for the feature “age” is shown in table II.

Table 3 show an instance of Iranian dataset after data preparing and converting variable (fuzzy features) to corresponding level. First column is the set of selected features, the second one is the value of features for a requested facility which is accepted as a low risk one and the last is the value of features for the rejected facility. In this table the fuzzy features are shown bold. The ten first rows in the table 3 are shown the status of the dedicated facilities and also the number of them for each person, which are use especially in this country.

Table 2. Levels and Their Interval of Linguistic Variable Age

Level	Its interval
L1	20 – 33
L2	30 – 44
L3	39 – 53
L4	50 – 65
L5	61 – 74
L6	70 – 83
L7	80 – 90

Table 3. An Instance of Iranian Dataset

Features	Low risk. credit scoring	high risk. credit scoring
Type1-active	1	1
Type1-expired	0	0
Type1-delayed	0	1
Type1-doubtful	0	0
Type1- settled	1	0
Type2-active	3	2
Type2-expired	0	0
Type2-delayed	0	0
Type2-doubtful	0	0
Type2- settled	0	0
No guarantee	5	4
Guarantee value	103178	391714
Sex	1	0
Age	42	38
Education	7	5
Marital status	2	2
Career	8	22
No returned check	3	0
Deposit account ($)	1352	8147
Deposit period (month)	121	65
Average salary($)	1400	2628

• V.    E VALUATION

The fuzzy expert system was executed as a independent process on several datasets likes Australian credit, German credit and Ansar Bank dataset to determine whether or not the loan is paid. Then the model was reviewed by experts and university's professors. The results of different methods are shown in table 4.

The result of fuzzy expert system for Iranian dataset was evaluated by18 experts of the best. They are requested to explain about the output of fuzzy system. Each expert could choose one of the four situations "perfectly agree", "good", "indeterminate" and "disagree". The result was shown in table 5.

Table 4. Rresults of Several Methods on Each Dataset

	Australian credit	German credit	Iranian credit
LRA	87.25	76.3	69.86
LDA	85.96	72.6	71.22
MLP	85.84	73.28	70.92
RBFN	87.14	74.6	69.47
DT	84.39	72.1	74.23
Bagging_DT	86.38	76.45	79.64
Random_Subspace_DT	86.93	76.12	78.28
Random_Forest	86.89	77.05	75.22
Rotation_Forest	86.55	77	79.8
RS-Bagging_DT	88.17	78.36	83.56
Bagging-RS_DT	88.01	78.52	81.88
fuzzy expert system	93.21	83.56	92.3

Table 5. Experts' Viewpoints for Fuzzy System

View point	No
Perfectly agree	11
Good	5
Undetermined	0
Disagree	2

VI. C ONCLUSION

As results and evaluation were shown, fuzzy system could get good outcome for solving the bank customer classification problem for several datasets. The remarkable improvement in the efficiency is to extract rules using the dataset. Furthermore, the dependence of the expert was removed. So the percentage error would the expert has on this model had no effect on creating it. Due to the nature of fuzzy rules, they are describable and experts could confirm or reject the validity of its decision. This method has another advantage that it could adapt by changing rules, because the rule is applied on the data and rule is extracted based on data. So this expert system is not designed only for a bank or particular database.