Basis set superposition error: effects of atomic basis set optimization on value of counterpoise correction

On the way to the hydrogen economy, several problems should be solved. Among one of them is the creation of effective and compact hydrogen storages. Carbon nanostructures are promising materials for such utilization since they have unique mechanical properties [1, 2], porosity, low density and high surface area [3]. However, there are numerous allotropes of carbon. Therefore, in search of a material with the needed properties, computer modelling could decrease the experimental costs and shorten trial and error loop.

Density functional theory, a popular approach in atomistic simulations, allows researchers to obtain precise results even for big systems [4], which can be useful in modelling of, for example, carbon nanotubes (CNTs), where simulation cell could contain up to several hundred atoms [5]. Though this method does not require empirical data of a simulated system, to reduce the many-electron problem to one-electron, some theoretical approximations are needed.

One of the key approximations is the wave function decomposition over a certain finite basis. The most common approaches are localized pseudoatomic orbitals (PAOs) and plane waves. For big systems or structures with a large vacuum volume (like in the case of adsorption modelling), PAOs are an effective method since they give accurate results with the low computational cost [6]. However, PAO basis set is prone to a significant basis set superposition error, BSSE (an over-estimation of binding energy due to the unequal basis sets between the interacting bonded system and non-interacting separated systems), in weakly interacted systems [7]. To reduce BSSE, counterpoise (CP) correction by Boys and Bernardi [8] can be used. Though, it is not clear, how atomic basis set optimization influences the value of this correction and corrected hydrogen adsorption energy. And if it is possible to get similar to the BSSE-free plane-waves results, using PAOs.

Therefore, in this work, we consider different allotropes of carbon and their interaction with the molecular hydrogen. For each carbon system, we optimize PAO basis set (for carbon atom). Then we calculate CP-corrected hydrogen adsorption energies before (with the default SIESTA basis set parameters) and after basis set optimization. The resulting hydrogen adsorption energies for 2D structures are com- pared with the BSSE-free plane-wave basis calculations. Additionally, we perform delta-test of utilized DFT packages, using different PAO basis set parameters.

Models and simulation parameters

Spin-polarized DFT calculations were performed in SIESTA package [9, 10], where PAOs are implemented as a basis set. Adsorption on 2D carbon structures (CEY and GDY) was also investigated using the Vienna ab initio simulation package (VASP) [11] with the projector-augmented wave (PAW) method [12] and BSSE-free plane-wave basis set. The local density approximation, LDA (Ceperley– Alder functional [13]), and the generalized gradient approximation, GGA (Perdew–Burke–Ernzerhof functional [14]), were employed as the exchange-correlation functional. Geometry relaxation was performed by the conjugate-gradient method. For all SIESTA calculations, pseudopotentials were taken from the FHI pseudodatabase [15]. In the VASP simulations, we used the 2012 version of pseudopotentials, which treats the following electrons as valence: 1s for H and 2 s ²2 p ² for C.

Carbon nanotubes . We considered internal and external adsorption of a single hydrogen molecule on the pristine CNT(5,5). The simulation cell contains four primitive cells of the nanotube (80 carbon atoms in total). The optimized translational parameter in GGA (LDA) is 9,87 Å (9,78 Å). In nonperiodic directions (perpendicular to the tube’s axis) we put ~100 Å of vacuum. The force convergence criterion is 10^–4 Ry/Bohr. The mesh cut-off [16] is 360 Ry (210 Ry) for GGA (LDA) calculations. With the 1 X 1 X 32 Monkhorst-Pack set of k -points, the numerical precision of hydrogen adsorption energy calculations is 10 meV.

En-yne . We considered the adsorption of a single hydrogen molecule. The simulation cell contains two primitive cells of the CEY (20 carbon atoms in total). SIESTA simulation parameters: optimized sizes of an orthorhombic cell for GGA (LDA) calculations – 11,28·9,76·50 ų (11,20·9,69·50 ų); the mesh cut off for GGA (LDA) calculations - 350 Ry (210 Ry); k -points set - 11 X 11 X 1; the force convergence criterion – 5·10^–5 Ry/Bohr. All these parameters allowed us to calculate hydrogen adsorption energies with the precision of ~7 meV. VASP simulation parameters: optimized sizes of an orthorhombic cell for GGA (LDA) calculations – 11,26·9,74·20 ų (11,20·9,69·20 ų); plane-wave basis set cut-off - 600 eV; k -points set - 9 X 9 X 1; the force convergence criterion - 10^-3 eV/А. All these parameters allowed us to calculate hydrogen adsorption energies with the precision of ~3 meV.

Graphdiyne . We considered two configurations of a single hydrogen molecule: on top of the big trigonal pore, and on top of the small hexagonal pore. The simulation cell contains one hexagonal GDY primitive cell (18 carbon atoms in total). SIESTA simulation parameters: the optimized translational parameter in GGA (LDA) is 9,48 Å (9,39 Å), the distance between the structure and its image – ~ 100 Å; the mesh cut off for GGA (LDA) calculations - 350 Ry (210 Ry); k -points set - 9 X 9 X 1; the force convergence criterion – 5·10^–5 Ry/Bohr. All these parameters allowed us to calculate hydrogen adsorption energies with the precision of ~ 7 meV. VASP simulation parameters: the optimized translational parameter in GGA (LDA) is 9,46 Å (9,39 Å), the distance between the structure and its image – 20 Å; plane-wave basis set cut-off - 600 eV; k -points set - 9 X 9 X 1; the force convergence criterion -10^–3 eV/Å. All these parameters allowed us to calculate hydrogen adsorption energies with the precision of ~ 3 meV.

PAO basis set optimization

For basis set optimization, we used the methodology described in [17]. For all considered structures (pristine CNT, CEY, and GDY), we separately optimized basis set parameters for carbon atoms. All parameters for hydrogen were taken from [17]. Since all considered adsorbents consist of one atom type (carbon), during the basis set optimization, we tracked only the structure total energy and the characteristic bond length.

As an example, in Fig. 1 we demonstrated the optimization procedure for C(2 p ) orbital in the case of CEY. In the presented example, we chose the optimal values for orbital cut-off and SplitNorm using the criterion of minimal total energy. Additionally, we monitored the length of a C-C bond, d e _ _c . After orbital cut-off reached the value r_cut = 7,5 Bohr, d_C - _C remains on the same level (1,3942 А). Since bigger r_cut employs higher computational costs, we chose r_cut = 7,5 Bohr as an optimal value. The dependence of the structure total energy on SplitNorm parameter has a pronounced minimum at SplitNorm 0,25 , which has been chosen as an optimal value.

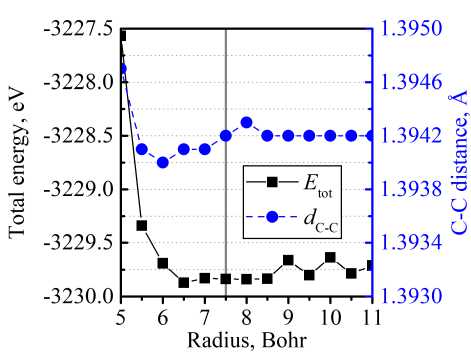
a)

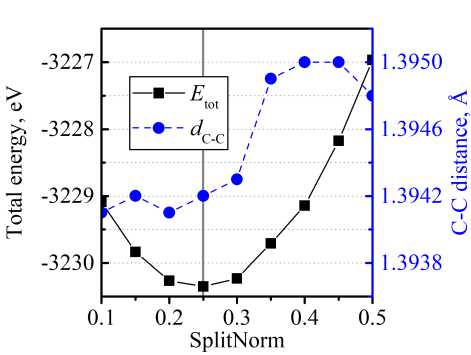
b)

Fig. 1. Dependence of CEY total energy and C–C bond length on a) cut-off radius of С(2p) orbital; b) SplitNorm parameter of С(2p) orbital. Solid grey lines note the chosen value of orbital parameters

Optimal basis set parameters are shown in Table 1 ( rmcut is a cut-off radius of a modified orbital, it derives from rcut and SplitNorm). For comparison, we also presented optimized parameters for graphite and default PAO parameters in SIESTA.

Table 1

Optimal parameters for С(2 s ) and C(2 p ) orbitals for different carbon allotropes

Structure		CNT	CEY	GDY	Bulk	Default PAO
C(2 s )	rcut , Bohr	8,03	8,66	8,03	7,64	4,09
	SplitNorm	0,27	0,35	0,35	0,35	0,15
	rmcut , Bohr	3,03	2,81	2,81	2,81	3,35
C(2 p )	rcut , Bohr	10,06	7,64	9,57	8,66	4,87
	SplitNorm	0,26	0,24	0,20	0,24	0,15
	rmcut , Bohr	3,18	3,27	3,52	3,27	3,48

Table 1 shows that, firstly, for different reference systems, we got slightly different optimal basis set parameters using the same pseudopotential in all cases. Secondly, all optimized parameters differ noticeably from the default ones (especially, r_cut ). Therefore, default basis set parameters should be used cautiously, and each new system requires basis set optimization.

Delta test

To compare used DFT packages (VASP and SIESTA), we performed the delta test [18] between SIESTA results for different sets of orbital parameters and VASP data [19]. The obtained results are presented in Table 2.

Table 2 shows that the biggest А С (and, consequently, the worst agreement with the VASP data) was obtained with the default basis set for carbon. Furthermore, different PAO basis sets resulted in different delta parameters (it can be seen in relative А _С ). Generally speaking, the reference system used in the current version of delta test is a bulk structure (and for this reason delta test cannot be used for comparison of pseudopotential, for this purpose consideration of different allotropes is needed). Therefore, to compare DFT packages, where atomic basis sets are utilized, it is necessary to optimize PAOs parameters on the needed reference system (bulk). So, the correct value in our case is А _С for graphite: А С = 0,36 meV/atom. This small value implies the good agreement between VASP and SIESTA results for carbon structures with the used pseudopotentials (results of the delta test considerably depend on the quality of pseudopotentials).

Table 2

a )

b )

c )

CP-corrected hydrogen adsorption energies

We simulated the adsorption of a single hydrogen molecule on CNT(5,5), CEY, and GDY. Relaxed structures are presented in Fig. 2.

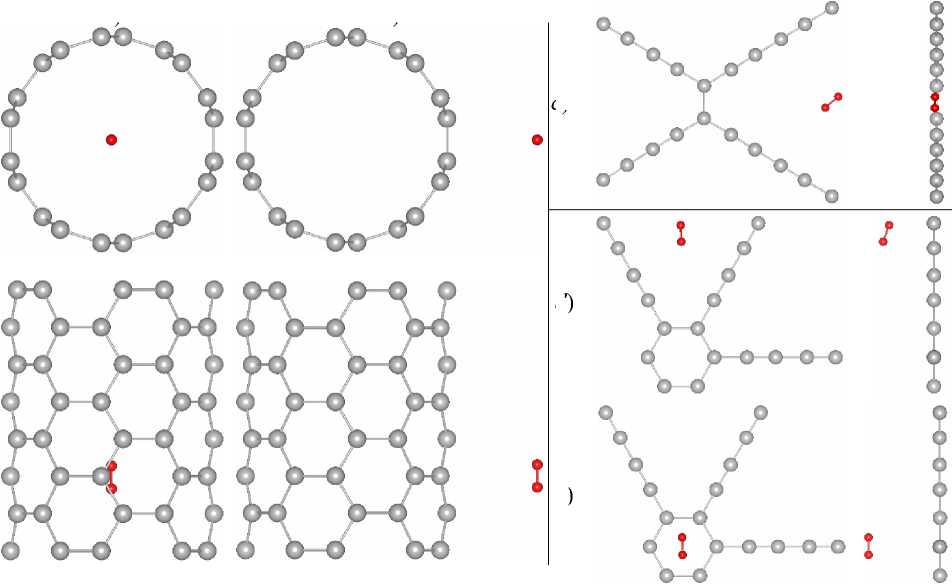
d )

e )

Fig. 2. Relaxed in SIESTA (GGA) structures of adsorbed hydrogen on: a) internal surface of CNT(5,5); b) external surface of CNT(5,5); c) CEY; d) top of the GDY big pore; e) top of the GDY small pore.

Carbon and hydrogen atoms are grey and red, respectively

Delta parameters, obtained for different PAO basis sets

Structure	CNT	CEY	GDY	Bulk	Default PAO
А С , meV/atom	1,88	1,47	0,32	0,36	2,86
Relative А С , %	15,1	11,8	2,6	2,9	22,4

Hydrogen adsorption energy was calculated as follows:

BSSE

E bind = E base ⁺ E H2

^^^^^^^е

E base +H2 ,

where E base _+H2 is the total energy of a complex “carbon nanomaterial + hydrogen molecule”, E base is the total energy of a carbon nanomaterial, E _H2 is the total energy of an isolated hydrogen molecule. Here, if E bi _nd >  0 , hydrogen attracts to the base structure, and the bigger is E bi _nd the stronger is this binding.

CP corrections by Boys and Bernardi were calculated as follows:

ECP = Ebase - ghost - Ebase + EH2 - ghost - EH2 , where Ebase_ghost is the total energy of a carbon nanomaterial calculated in the full basis of a complex “carbon nanomaterial + hydrogen molecule”, Eb0ase is the total energy of a carbon nanomaterial calculated in the basis of a carbon structure, EH2 _ghost is the total energy of a hydrogen molecule calculated in the full basis of a complex “carbon nanomaterial + hydrogen molecule”, EH02 is the total energy of a hydrogen molecules calculated in the basis of this molecule. All these energies are calculated in relaxed geometries presented in Fig. 2 without further structural optimization. This correction, ECP , should be always negative. Then the final hydrogen adsorption energy was calculated as Ebind = EbBiSnSdE +ECP . The results of hydrogen adsorption energy calculations, as well as the value of CP correction by Boys and Bernardi, are presented in Table 3.

Table 3

Hydrogen adsorption energy (meV) and the value of CP correction by Boys and Bernardi (meV)

Basis set	CNT(5,5)				CEY		GDY
	external		internal				big pore		small pore
	E bind	E CP	E bind	E CP	E bind	E CP	E bind	E CP	E bind	E CP
GGA
optimized	5	44	35	231	12 (18)	43	8 (15)	47	10 (14)	57
default	–15	205	22	318	40	230	–34	369	–17	184
LDA
optimized	70	71	238	234	104 (105)	44	120 (122)	86	91 (87)	110
default	69	233	168	345	112	301	127	428	169	117

Table 3 shows that almost in all cases E_CP drops after basis set optimization (for example, in the case of GDY big pore, E_CP decreased by almost 8 times). However, even with the optimized basis set, E_CP is significant in comparison with E_bind (especially for GGA calculations). Mostly, in LDA calculations E_CP is bigger than in GGA calculations, though, as expected, E_bind is bigger too (since LDA overestimates the energy of vdW interaction, and GGA underestimates it [20]). As a result, E_CP / E_bind is lower in LDA calculations than in GGA. All in all, we have not found the general trend in E_bind and basis set optimization. In some cases (for example, LDA calculations of external adsorption on CNT(5,5) or adsorption on top of the GDY big pore) E_bind changes only slightly after basis set optimization, while in other cases the change in E_bind can be significant.

To compare results, obtained with PAO basis set, with the BSSE-free plane-wave basis, we calculated hydrogen adsorption energies on 2D carbon nanomaterials in VASP. Results of these calculations are presented in Table 3 within the brackets. And the difference between the CP-corrected hydrogen adsorption energies, calculated with the optimized basis set, and the VASP adsorption energies is within the numerical precision. This is not true for E_bind obtained with the default basis set of carbon. To summarize, if one wants to get fast and precise hydrogen adsorption energies in weakly interacting systems, using PAOs, one should both optimize the basis set and employ CP correction by Boys and Bernardi.

Conclusions

In this work, we obtained the optimal parameters of PAOs basis sets, implemented in SIESTA, for CNTs, CEY, GDY, and graphite. The delta-test of VASP and SIESTA showed good agreement for carbon ( А С = 0,36 meV/atom). Simulation of hydrogen adsorption on low-dimensional carbon nanomaterials indicated the necessity of basis set optimization for each considered system and BSSE correction in the case of atomic basis set usage for modelling of weakly interacted systems. If these are done, the resulting adsorption energies will coincide with the ones, obtained with the BSSE-free plane-wave basis, within the numerical precision.

The reported study utilized the supercomputer resources of South Ural State University [21].