Bat-Genetic Encryption Technique
Автор: Hamdy M. Mousa
Журнал: International Journal of Intelligent Systems and Applications @ijisa
Статья в выпуске: 11 vol.11, 2019 года.
Бесплатный доступ
Nowadays, the security of confidential data is the vital issue in the digital world. Information security becomes even more essential in storing and transmitting data while online. For protecting digital data and achieving security and confidentiality over an insecure internet, the iterative Bat-Genetic Encryption Technique (B-GET) is proposed. The main stages of B-GET are pre-processing, encryption process, bat algorithm steps, and genetic processes. B-GET also comprises an arithmetic and logical operators that increase encryption quality. Empirical results show that the reconstructed data is a copy of the original. It also demonstrates that B-GET technique has a large space key and several defensive stages that resist many attacks and it has strong security based on multiple steps, multiple variables, and the main stages of the B-GET technique. Encrypted data is nearly random and does not contain any indication to secret data.
Bat Algorithm, Cryptography, and Genetic Algorithm
Короткий адрес: https://sciup.org/15017104
IDR: 15017104 | DOI: 10.5815/ijisa.2019.11.01
Текст научной статьи Bat-Genetic Encryption Technique
Published Online November 2019 in MECS
There are numerous security difficulties during processing and transmission of digital contents over unconfident networks. Consequently, the crucial need for robust and efficient security techniques is vital demand. The main purposes of information security are permitting information to authorized one, covert information from all others, handling risk management during warehousing and transmission and enhancing authenticity processes [1, 2].
Nowadays, there are many security methodologies for protecting digital contents from attackers. One of them is cryptography. It is the science for encrypting and decrypting digital data so that data cannot be revealed by anyone except the authorized one. Symmetric-key and public-key algorithms are the categories of encryption algorithms. The same key is used for the encryption and decryption processes in the symmetric algorithms, but, in public key algorithms, there are different keys for encryption and decryption processes [3].
The second methodology is steganography that is used to hide the secret data into another data to be apparently invisible [4]. The third methodology is digital watermarking which is the process of inserting digital content into another digital content to protect from illegal operation and copying. Block and stream cipher are encryption methodology. A block cipher divides secret data to blocks and treats each block individually then, the encrypted output is produced. For better security, block size/length and the key must be large [5].
The well-known methodology among of the information security is the cryptography for protecting secret information. Cryptography is comprised of replacement and scrambling of data for confirming secrecy of information.
Kerckhoffs' Principle states, "the strength of a cryptosystem depends only on the key and, in particular; the security does not depend on keeping the encryption algorithm secret" [6]. Dependent on this principle, the vital features for determining the power of encryption technique are key length and operation's functions. A strong encryption technique must confirm confusion and diffusion requirements and strong against cryptographic attacks. The well-known encryption techniques i.e., DES, AES, IDEA, RSA, etc. are used for protecting data in many applications and achieved good results [1, 7].
The most previous encryption techniques in real-time applications have many challenges and suffer from computation cost. Therefore, many researchers propose techniques to resolve efficiently the security difficulties. Nevertheless, their proposed techniques have some performance and security issues, and exposed for some types of attacks.
This paper proposes a Bat-Genetic Encryption Technique (B-GET) that is a symmetric technique to encode a secret data. B-GET depends on standard Bat Algorithm, some of the arithmetic and logical operators and genetic algorithm processes. B-GET composes of pre-processing, symmetric key encryption and genetic processes encryption stage. In this technique, the secret data converted into binary. In addition, define and generate initial values for control parameters of Bat and genetic algorithms. In each round, encrypt the secret data with the key, determine the frequency, velocity, and location of each bat using bat algorithm. The velocity value defines the zone that will encrypt using arithmetic and logical operators. In addition, the genetic processes (crossover and mutation) are applied to scramble the data. The secret data may be any digital data (image pixels, audio, video, text, word document, etc.). The proposed technique is tested using the color and gray images. Images are the most usage on the internet among the other digital data and they have special features. Experimental results demonstrate that recreated data is a typical copy of secret data. They also show that the proposed technique is an efficient encryption technique.
The remaining of this paper is organized as follows: section II briefly introduces the related work, the original bat algorithm is explained in section III, the brief overview of genetic algorithm is presented in section IV, the proposed technique is explained in detail in section V; the experimental results are shown, discussed and evaluated in section VI. The obtained security results are satisfied. Lastly, concluding comments are mentioned.
-
II. Related Work
Several researchers have concentrated their researches on determining security demands and challenges of cryptography dependent on the application. Some of the related works are introduced in this section.
The authors propose hybrid encryption Procedure based on AES and Tiny Encryption Process. The data is encoded using tiny-AES-128 encryption process and authentication to alterations into cipher data. This hybrid procedure is used to improve encryption, performance, minimize recourses usage [8].
In paper [9], Tigris cipher is designed based on pure algebraic, cryptography basis and secret-key block cipher that is applicable for a limited resource environment and securing fast encryption. Many researchers proposed cryptography systems for increasing the security level and quality of the encrypted data using a fuzzy logic system [10,11,12,13]. The authors proposed cryptography systems based on DNA by generating a DNA encoding table for encoding or mixed DNA and Genetic algorithm to achieve confidentiality for secret data [14, 15, 16]. New intrusion detection model is introduced based on mixed between Naïve Bayes classifier and Bat Algorithm. Feature selection is carried out using the bat algorithm in Distributed Environment and using Naïve Bayes classifier for training and testing [17].
Many cryptosystems implement to permute the pixel positions and alters pixel values in plain-image using the chaotic map for enhancing the strength of encryption and achieving high security [18,19,20,21]. A many of researches have been done to achieve information security and confidentiality.
-
III. Bat Algorithm
Bats are animals that have the capability of echolocation. Bats emit series of sounds with a short and high frequency to the environment and listen to the echoes of those sounds. They use these echoes to discover and detect the victim’s shape, distance and direction, and escape close obstacles objects. During the bats fly to search to their prey, the rate of pulse emission and frequency are adapted. The wavelengths and loudness of a pulse are proportional to their prey sizes and distance.
A group of bats flies randomly to search the prey and each bat assigns interactive parameters such as location, velocity, frequencies, pulse rate, and loudness. Each bat modifies its parameters based on nearness to its target, its capability to adjust them and global best location of its group. Each parameter has a value in between it minimum and maximum range. For example, a frequency is in the range [minimum and maximum frequency].
Xin-She Yang developed the Bat Algorithm (BA) in 2010 [22]. The echolocation of the bats is the basic idea for this algorithm. The bats emit sound then, listen to their echoes for discovering the food and avoiding obstacles.
Yang [22] assumed three rules to formulate and implement the bat algorithm that are:
-
1. All bats have the ability to know the distance between it and the food/prey or background barriers and distinguish them by using echolocation.
-
2. Each bat in-group flies randomly with velocity ( v i ) at position ( x i ) with frequency ( f i ) to search for its food. It can modify wavelength ( λ ) and loudness ( Ai ) and regulate the rate of pulse emission ( R ) based on the nearness of its target.
-
3. The loudness varies from a maximum positive value to a minimum value.
For simplicity, there are minimum and maximum range [ f min , f max ] for frequency and BA is used no ray tracing in estimating the time delay and three-dimensional topography. The pseudocode of the original BA is as in Fig.1.
Pseudocode of the Original Bat Algorithm (BA) :
Objective function f(x), x = (x 1 , ..., x d )T
Initialize the bat population x i (i = 1, 2, ... , n) and v i
Define pulse frequency f i at x i
Initialize pulse rates r i and the loudness A i
While (iteration < Max number of iterations) Do
Generate new solutions by adjusting frequency, and updating velocities and locations/solutions as the equations (1) to (3).
If (rand > r i )
Select a solution among the best solutions
Generate a local solution around the selected best solution
End if
Generate a new solution by flying randomly
If (rand < A i & f(x i ) < f(x∗) )
Accept the new solutions
Increase r i and reduce A i
End if
Rank the bats and find the current best x∗
End while
Post process results and visualization
-
Fig.1. Original Bat Algorithm
In the original BA, the behavior of bat is captured into the fitness function of the problem to be solved. It consists of the following components: Initialization, Local search, Generation of a new solution by flying randomly and find the current best solution.
The initial population of bats is randomly generated. The following equations determine the moving of the virtual bats to create a new solution.
f=fm m + ( fm x -f n™ ) в
Ч '( t ) = VZ ( t-1 ) + ( хг -( t-l ) -x * ( t-l ) ) f (2)
x i ( t ) = x i ( t-1 ) +v , -( t ) (3)
Where β is randomly generated value and it is in the range [0; 1], x* is best location of all bats and t is time. After the best solution is defined among the solutions then, for the local search, bat randomly modifies the current location according to the equation:
x new = x old + E A ( t ) (4)
Where e is a random number and A(t) is average loudness of all bats at this time.
The local search is depended on pulse rate emission ( ri ) and loudness ( Ai ). These two parameters are tuned based on natural characteristics of the bat until bat finds its prey. The following equations give mathematically model of these characteristics.
A i ( t ) =^ A i ( t - 1 ) (5)
R ( t ) = R i ( 0 ) ( 1 - exP ( -Y t ) ) (6)
Where a and y are constants. A i and R i is loudness and pulse rate of Bat “ i “ at the time ( t ).
-
IV. Principle of Genetic Algorithms
Genetic algorithms (GAs) are population-based metaheuristic optimization algorithms. GA generates new solutions according to the Individuals’ fitness. GA composes of a population of chromosomes, selection, crossover, and mutation to produce a new generation (offsprings) [23].
The population of chromosomes is randomly initiated with a set of the problem’s solutions. Based on the fitness of the current population, select the fittest solutions, which are used to generate a new one (off-springs). The selection and generation processes are repeated until one of the termination conditions are satisfied. Fig.2. shows the steps of the basic genetic algorithm.
Determine the number of chromosomes, Maximum generation number, and mutation rate and crossover rate value.
Generate random population of chromosomes.
Evaluate the fitness of each chromosome.
While (generation number > Maximum generation number OR fitness is met)
Evaluation of fitness value of chromosomes by calculating objective function
Chromosomes selection process
Crossover process (Single/Two-point-Uniform- …)
Mutation process
Evaluate the fitness of each chromosome.
End While
Output Solution (Best Chromosomes)
-
Fig.2. Basic Genetic Algorithm
-
V. Bat Genetic Encryption Technique
In general, all security techniques protect information and data from any illegitimate activities. Due to increasing of computing power, the significant parameters, those making security algorithms strong and unbreakable, are time and computational complexity. To achieve the requirements of the security system, the symmetric cryptography and iterative process technique are proposed. The proposed technique is contingent on the standard bat algorithm, some of the arithmetic and logical operators, keys and genetic algorithm processes. This technique encrypts any digital data type. The main steps of the proposed technique are pre-processing, symmetric key encryption, bat algorithm, and the genetic operation encryption stage. They are explained as follows.
-
A. Pre-processing Stage
The main objective of this stage is transformed the secret data into n-Dimension ( nD ) array of bytes. Where n is an integer value. After reading the secret data in 8-bits Binary format, reshape it to suitable array dependent to its size.
The pre-processing stage of B-GET depends on the type of secret data file and its format. Grayscale/color image is ready to manipulate by B-GET because its shape is two/three-dimensional (2/3D) array structure. In the video file case, separating its components and getting the properties of the video file. In text file case, conversion to ASCII values and reshapes it to vector or 2D array in this stage. In other data-type file cases, read it as the 8-bit unsigned integer (uint8) then reshapes secret data to a 2D array.
-
B. Encryption Stage
The original input data is treated as a simple nD array composed of bits "0" and "1". After reading the secret data, encrypt it using symmetric secret key(s) and/or a suitable number of bats change the values of entire secret data one time or more. After the data are split contiguous/ overlapping regions, then, the bat alters the values of these regions.
C Bat Algorithm
The bat algorithm (BA) was first presented in [22]. BA has also been successfully applied and used in many fields especially as optimization problem [24,25,26], clustering problem [27,28] and many other problems [29,30,31,32].
Due to bat’s echolocation features, frequency-tuning system, automatic zooming, a variation of loudness and dissimilarity pulse emission rates, exploration and exploitation of searches, and many other features. BA combines a good mixture of main advantages of metaheuristic algorithms and it is theoretically more powerful than other meta-heuristic algorithms [22]. According to best of my knowledge, this algorithm was not been previously taught or tested in the cryptography field. These mentioned characteristics of BA have paid my attention to select this algorithm for cryptography task.
-
a. parameters Representation
The frequency ( f(Bat) ) is a positive integer or float number and its value varies in a range between minimum and maximum. P(Bat) is predefined positive value without boundary range that will affect the frequency as illustrated in equation (7).
f ( Bat ) = fmin ( Bat ) +
( fmcx ( Bat ) -fmin ( Bat ) ) в ( Bat )
Where f min (Bat) and f max (Bat) are predefined minima and maximum bat's frequency values respectively
The velocity of each bat ( v(Bat,t) ) is represented as a positive integer number and the velocity is up, down, left or right direction based on f(Bat) . Velocity determines region which; the bat should be changed (encrypted) using the arithmetic and logical operators at a certain time as illustrated in Fig.3. The region shape is square in B-GET implementation.
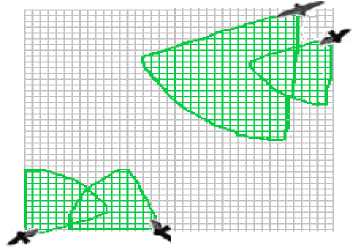
Fig.3. Bat Motion
Each bat in-group will interacted with others for determining the global best location ( x* ). The x(Bat, t - 1) value is a positive integer that represents the current bat's location. Each bat updates its velocity according to the equation (8).
v (Bat,t-1) + v (Bat,t)
< Г x ( Bat, t -1 )^ _. -x * ( t-1 ) >
> mod(upper)
f ( Bat )
The smallest value of velocity is one and upper boundary value ( upper ) must be predefined.
In the proposed technique, each bat’s location ( x(Bat, t) ) is formulated as two positive integers that have two boundaries, where the upper boundary is the size of secret data. Each bat’s location is updated according to equation (9).
x ( Bat,t ) = x ( Bat,t-1 ) + v ( Bat,t ) (9)
In fact, the choices of minimum and maximum values are based on the size of secret data and may affect the speed in cryptography processes.
-
b. Loudness Representation
The loudness of any bat ( A(Bat) ) is represented as a positive integer, which will be changed as in equation (10).
A ( Bat , t ) =^ A ( Bat , t - 1 ) (10)
Through iterations, the loudness value will decrease/increase. Equation (10) determines the amount of decrease/increase based on predefined value (α). The loudness slightly modifies the new bat’s location according to equation (11).
x ( Bat , t ) = x ( Bat , t ) + s Aav ( t ) (11)
Where Aav(t) is the average loudness of all the bats at a certain time, while ^ is a predefined value. The sound loudness ( A(Bat, t ) has the maximum loudness and minimum loudness. Sound loudness value has a good role in getting cipher data.
-
c. Pulse Rate Representation
The pulse rate of bat ( R(Bat, t) ) value plays a good role in the rate of diffusion/confusion. The amount of increase/decrease in pulse rate value will be determined at instant t accordingly the γ value as defined in the equation (12).
R ( Bat , t ) = R 0 ( Bat ) [ 1 - e -Y t ] (12)
Where R0 is predefined constant value for each bat and t is iteration number. Variation of A(Bat, t) and R(Bat, t) values have considerable effects in the obtained data.
-
D. Genetic encryption stage
The encryption system generally consists of two stages. The first one is confusion that replaces values of data and the other is diffusion that modifies values of data. The main role of genetic encryption stage is data confusion. As known, the GA includes the following processes: selection, crossover (single point, Two-point, uniform …) and mutation [33].
The proposed system defines a number of operations based on the arithmetic operators, logical operators, and genetic algorithm processes. These operations are used for relocating and modification values of secret data. The types of operations and locations' indices define using loudness pulse rate function and iteration number.
Samples of functions, which may use in B-GAT are clarified in the following:
-
• Swap 2 Rows/Columns (S2RC(RCn, RCn+1)): row/column is exchanged with another.
-
• Row/Column Crossover (crossRC(RClndex, Tcro ss )): Determine two rows/columns consecutively (index and index+1) and crossover type (Single/Two-point-Uniform- Arithmetic-Ring-Shuffle …), then perform crossover process.
-
• Row Column Crossover (crossR_C(Rindexr, Clndexc, Tcross)): Determine Row and Columns (Rindexr and C indexc ) and crossover type (Single/Two-point-Uniform-Arithmetic-Ring-Shuffle …), then perform the crossover process.
-
• Row/Column Complement (compRC(lndex)): blt
complement data’s row/column value.
-
• XOR/XNOR Cell mutation mutateC(lndr, Indc):
change the value in (indr, indc) with the result of XOR / XNOR operation between the value in (indr, indc) and Loudness or Pulse rate or Iteration number (value).
Row ( indr , indc ) = XOR ( Cell ( indr , indc ) , value )
Or;
Row ( indr , indc ) = XNOR ( Cell ( indr , indc ) , value )
-
• Row/Column addition ( addRC((R)): add cells with one/two level (index, index+1, index+2) in the same row. The first level is performed as equation:
RC ( ind ) = (( RC ( ind )) + ( RC ( ind + 1) > 255)( - 255) + (( RC ( ind )) + ( RC ( ind + 1)))
The other level is operated as equation:
RC ( ind ) = (( RC ( ind )) + ( RC ( ind + 2)) > 255)( - 255) +
(( RC ( ind )) + ( RC ( ind + 2)))
-
• Row/Column subtraction (subRC((RC)):
subtract cells with one/two level (index, index+1, index+2) in the same row. The first level that subtract row (index) from row(index +1) and is operated as equation:
RC ( ind ) = ( ( RC ( ind ) ) - ( RC ( ind + 1) < 0 ) ( 256 )
-
+ ( ( RC ( ind ) ) - ( RC ( ind + 1 ) ) )
The second level is done as the equation:
RC ( ind ) = ( ( RC ( ind ) ) - ( RC ( ind + 2 ) < 0 ) ( 256 ) + ( ( RC ( ind ) ) - ( RC ( ind + 2 ) ) )
It is also used other operation that increases the efficiency of encryption process i.e. row/column subtraction from or addition to keys, iteration number values. All operation and processes are instantaneously performed for achieving efficient and robust security technique. Fig.4 shows the main stages of B-GET.
The final stage is responsible for reshaping the encrypted data to equivalent original form with reserved data and save it.
Fig.4. Stages of B-GET
Input: Read Secret data (text/Image/… ) .
Output: encrypted (text/Image/….) file
Initialize parameters (No of iteration, No. of bats, starting location, velocity, solution, pulse rate, loudness, best, f max , f min , direction, α , γ , β , ε , …
Pre-processing secret data
BData ^ encrypted secret data file with key(s) or/and bat scramble process
While t < No of iteration
BData ^ encrypted secret data file with key(s)
For each bat
Calculate frequency, Update velocity, and Estimate location according to Equation (7), (8) and (9).
Check velocity Boundaries
Bat’s zone and check size boundaries
If (frequency value < predefined value)
Change Bat’s direction
End if
For k<= bat’s zone column limit // Column size
Perform arithmetic/logical operations
For k1 <= bat’s zone Row limit // Row size
Perform arithmetic/logical operations
Check Pulse rate
Estimate best* = sum(all bats’ pulse rate)
// Small variation in bat’s location
x(Bat)=best* + a . P(Bat);
if (β(Bat) < predefined value)
// The factor limits the step sizes of random walks
Bestm= sum(best(:)/Number of bats;
End if
// new position if false Check boundaries
Row/column_index= Row/column_index ± velocity (Bat, t) +1;
else
Row/column_index=other boundary (1 or End)
End if
End for // Row size
End for // Column size
Perform GA crossover and mutation, Update pulse rate and loudness, location
R(Bat)=R 0 (1-exp(- γ .t));
Average of loudness = ((sum(all bats’ loudness)) + R (Bat) ) / number of bats;
Bat’s loudness= average of loudness . ∝ + R(Bat) ;
Row/Column index= Function (t, bat’s loudness, pulse rate)
Crossover row/column process
If (bat’s loudness> predefined value)
Mutate cell
End if
End for //Bat
End while //iteration
Reshape Encrypted Data
Save encrypted data file
-
Fig.5. Pseudocode of proposed encoding B-GET
Input: encrypted data file
Output: secret data
Initialize parameters (No of iteration, No. of bat, starting location, velocity, solution, pulse rate, loudness, best, f max , f min , direction, α , γ , β , ε , …
Pre-processing secret data
While t<= No of iteration
For each bat
Calculate frequency, Update velocity, and Estimate location
According to equations (7), (8) and (9).
Check boundaries of velocity
If (frequency value < predefined value)
Change Bat’s direction
End if
// save processed parameters into array
Parameter ( Bat, t, :)=( Row, Column, v , A(Bat) ,… );
// update position
Check Pulse rate
Estimate best*=sum(all bats’ pulse rate)
//Small variation in bat’s location
x(Bat)=best* + а. P(Bat);
If b(Bat) // The factor limits the step sizes of random walks bestm= sum(best(:))/No. of Bats; End if // new position If false Check boundaries Row/column_index= Row/column_index ± velocity(Bat, t)+1; else Row/column_index=1 End if End for //Bat End while //iteration // Reconstructed While No of iteration > 0 R(Bat) =R0 (1-exp(-γ . t)); Average of loudness = ((sum (all bats’ loudness)) + R)/ number of bats; bat’s loudness= average of loudness . ∝ + R(Bat); row/column index= Function(t, bat’s loudness, pulse rate) Crossover row/column process If bat’s loudness > predefined value) Mutate cell End if For each bat Assign processed parameter form array Bat’s zone; Check size boundaries for k<= velocity (bat’s zone column limit) // Column size Perform arithmetic/logical operations for k1 <= velocity (bat’s zone Row limit) // Row size Perform arithmetic/logical operations End for // Row size End for // Column size End for //Bat BData^ decrypted secret data file with key(s) End while //iteration BData^ decrypted secret data file with key(s) or/and bat scramble process Reshape obtained Data Save secret data file Fig.6. Pseudocode of Proposed Decoding B-GET Example: To clarify how B-GET works and follows its steps to build its output. The simple example would be explained the main stage of B-GET. Encryption process stage: In this example, the size of the original input data is 8x8 bytes as shown in the Fig.7-a. There is one key or more for encrypting the data in this stage. First, the value of the symmetric key is (211). Fig.7-b shows the output of XOR operation between key and data. (a) Original Data 140 117 35 115 196 32 209 140 26 49 123 219 239 101 84 64 141 126 140 62 130 195 240 234 244 222 221 132 92 106 169 72 105 136 93 197 220 251 89 155 180 157 154 189 91 159 153 166 158 177 141 143 186 186 173 142 154 150 155 184 178 175 170 158 (b) Result of XOR Key (211) encryption 140 117 35 115 196 32 209 140 26 49 123 219 239 101 84 64 141 126 140 62 130 195 240 234 244 222 221 132 92 106 169 72 105 241 78 19 239 251 89 155 29 142 232 208 74 159 153 166 187 63 117 95 4 186 173 142 85 213 16 23 182 175 170 158 c)1st quarter of Bat Encrypt by 1st bat with constant v=4 , level1 add function 140 117 35 115 196 32 209 140 26 49 123 219 239 101 84 64 141 126 140 62 130 195 240 234 244 222 221 132 92 106 169 72 105 241 78 19 239 234 67 222 29 142 232 208 57 137 220 132 187 63 117 95 61 67 137 18 85 213 16 23 243 242 51 176 f) After 1st bat Encrypt with velocity=4, level1 add function (d) 2nd quarter of Bat Encrypt 95 166 240 160 23 243 2 95 201 226 168 8 60 182 135 147 94 173 95 237 81 16 35 57 39 13 14 87 143 185 122 155 186 34 157 192 60 57 144 13 206 93 59 3 234 90 15 87 104 236 166 140 238 144 90 193 134 6 195 196 32 33 224 99 (e) 3rd quarter of Bat Encrypt 95 5 245 149 172 159 161 0 40 231 157 157 148 85 40 147 134 148 252 138 205 101 75 204 173 161 10 225 149 30 197 103 103 42 209 114 11 98 183 43 53 135 12 117 0 188 198 130 157 115 178 1 227 76 32 67 35 121 117 197 230 109 0 166 95 100 89 238 154 57 161 0 135 75 246 139 46 142 40 147 13 223 242 21 251 243 75 204 186 128 252 246 144 17 197 103 33 170 205 104 155 115 183 43 86 49 217 221 155 47 198 130 157 115 178 1 227 76 32 67 35 121 117 197 230 109 0 166 (g) Result of second level of XOR Key (211) encryption 135 75 246 139 46 142 40 147 95 100 89 238 154 57 161 0 13 223 242 21 251 243 75 204 186 128 252 246 144 17 197 103 33 170 205 104 155 115 183 43 86 49 217 221 155 47 198 130 157 115 178 1 227 76 32 67 35 121 117 197 230 109 0 166 (j) After Rows Crossover (h) After 2nd level Bat Encrypt with constant v=4, level1 add function 155 115 183 43 46 142 40 147 155 47 198 130 154 57 161 0 227 76 32 67 251 243 75 204 230 109 0 166 144 17 197 103 33 170 205 104 135 75 246 139 86 49 217 221 95 100 89 238 157 115 178 1 13 223 242 21 35 121 117 197 186 128 252 246 (k)Swap region1 and region3 based on t, data size, Pulse rate and loudness (i) After Bat Encrypt with 1st bat with v=5, level1 add function 155 115 183 43 46 142 40 147 155 47 198 130 154 57 161 0 227 76 32 67 251 243 75 204 230 109 0 166 144 17 197 103 33 170 205 104 136 75 246 139 86 49 217 221 95 100 89 238 157 115 178 1 13 223 242 21 35 121 117 197 186 128 252 246 (l) Mutate cell (cell + t) (135 becomes 136) Fig.7. Encryption process 155 115 183 43 46 142 40 147 155 47 198 130 154 57 161 0 227 76 32 67 251 243 75 204 230 109 0 166 144 17 197 103 33 170 205 104 135 75 246 139 86 49 217 221 95 100 89 238 157 115 178 1 13 223 242 21 35 121 117 197 186 128 252 246 (a) Mutate cell (cell-t) (136 becomes 135) 135 75 246 139 46 142 40 147 95 100 89 238 154 57 161 0 13 223 242 21 251 243 75 204 186 128 252 246 144 17 197 103 33 170 205 104 155 115 183 43 86 49 217 221 155 47 198 130 157 115 178 1 227 76 32 67 35 121 117 197 230 109 0 166 (b) Before Swap region1 and region3 based on t, data size, Pulse rate and loudness 95 100 89 238 154 57 161 0 135 75 246 139 46 142 40 147 13 223 242 21 251 243 75 204 186 128 252 246 144 17 197 103 33 170 205 104 155 115 183 43 86 49 217 221 155 47 198 130 157 115 178 1 227 76 32 67 35 121 117 197 230 109 0 166 (c) Before Crossover swap row1 and row2 based on t, data size, Pulse rate and loudness 95 5 245 149 172 159 161 0 40 231 157 157 148 85 40 147 134 148 252 138 205 101 75 204 173 161 10 225 149 30 197 103 103 42 209 114 11 98 183 43 53 135 12 117 0 188 198 130 157 115 178 1 227 76 32 67 35 121 117 197 230 109 0 166 (d) Before 1st round 1st Bat Encrypt 95 166 240 160 23 243 2 95 201 226 168 8 60 182 135 147 94 173 95 237 81 16 35 57 39 13 14 87 143 185 122 155 186 34 157 192 60 57 144 13 206 93 59 3 234 90 15 87 104 236 166 140 238 144 90 193 134 6 195 196 32 33 224 99 (e) Before 1st level Bat Encrypt with 1st bat with constant v=4 , level1 sub function 140 117 35 115 196 32 209 140 26 49 123 219 239 101 84 64 141 126 140 62 130 195 240 234 244 222 221 132 92 106 169 72 105 241 78 19 239 234 67 222 29 142 232 208 57 137 220 132 187 63 117 95 61 67 137 18 85 213 16 23 243 242 51 176 (f) 1st level Key (211) encryption 140 233 174 80 81 92 177 187 142 188 88 104 103 69 131 180 115 77 17 99 104 94 156 170 103 96 81 70 71 167 185 94 117 170 128 65 166 145 176 83 180 157 154 189 91 159 153 166 158 177 141 143 186 186 173 142 154 150 155 184 178 175 170 158 g) Before 2nd level Bat Encrypt with 1 bats with constant v=4 , level1 sub function 95 58 125 131 130 143 98 104 93 111 139 187 180 150 80 103 160 158 194 176 187 141 79 121 180 179 130 149 148 116 106 141 166 121 83 146 117 66 99 128 103 78 73 110 136 76 74 117 77 98 94 92 105 105 126 93 73 69 72 107 97 124 121 77 h) Secret Data Before 2nd level Key encryption Fig.8. Reconstruction process Second Stage is bats encryption with updating their parameters. Afterward, all various parameters and variables are initialized; new values of them are computed according to bat algorithm. It is also determined the sequence of operations. In this example, a number of iterations are assigned to one and there is one bat with first level addition operation. The bat starts at (1, 1) position and its computed velocity is five. Bat's velocity equals five and it uses first-level addition operation to alter values in the square region from the cell(1,1) to the cell(6,6). Fig.7-i displays the output after bat encryption step. Update location (Bat) value based global best location and bat's parameters for random walks step sizes. The value of the parameter changes and the bat moves to a new position from (1, 1) to (7, 1), these new values are prepared to the next iteration. The second part of this stage is genetic algorithm processes. The first process is a crossover. There are two types: swap columns/rows or swap regions. The swap indices are a function of iteration, pulse rate, loudness values, and data size. An example of equations defines the regions' indices: Upper indices of region 1 (US1): US1 (i, j) = a. t + b < width / 2 Bottom indices of region 1 (BS1): BS1 (i, j) = c . Pulse + d . loudness < width / 2 Upper indices of region 2 (US2): US2 (i, j) = widths + a . t+b < width Bottom indices of region 2 (BS2): US2 (i, j) = width/^ + c . pulse + d . loudness< width Where a, b, c, and d are predefined variables. If outputs of these equations did not satisfy the width and height boundaries, then, split the data to 2/4 equal regions. If any dimension is odd, decrease it by one then, Row/2, Column/2, Row, and Column define boundaries. In Fig.7-j, row index is the iteration (t=1), then, swap rows1 and row2. The gotten indices are not suitable because they are larger than the width and height boundaries, then, fragment the data to four equal regions. Swap region1 and region3 as shown in Fig.7-k. The last step is cell mutation; the upper left cell is selected and replaces it with its value plus iteration (t) as shown in Fig.7-l. At this point, the encrypted process is completed and the final stage begins. Reconstruction process: At the beginning of reconstruction process, perform all stages of encryption process without modifying the data, just for follow back the values of beginning location, all control parameters and variable to store them in the array like the following example: Parameter (t, Bat) = (Row, Column, Velocity, Loudness,...) After that, execute the reconstruction process in reverse order of stages of the encryption process. The mutation, crossover and two levels of bat encryption and key encryption are performed as shown in Fig.8. At this point, the secret is discovered. For simplicity and testing purpose, the main program stages ware designed to handle two-dimensional secret data. Therefore, in the pre-processing of B-GET, all secret data are reshaped to a two-dimensional (2D) byte array format. Gray image is ready to manipulate by B-GET because its shape is a 2D array but, color image, red, green and blue components are individually processed. In the video file case, separating its components/frame and processing independently. The text file is reformed to the 2D array in the pre-processing stage. Read other datatype files as unsigned byte integer and transform secret data to the 2D array. If the size of data is not suitable to convert into a 2D array, expand it by padding with zero values. The B-GET is implemented by multi-functions (m-file) using MATLAB 2015. The B-GET is executed on Windows 7, 64-bit Operating system in AMD Athlon (tm) II X2 220 Processor, 2.80GHz and 4 GB RAM. Because of the growing use of images in commercial and community communication process, most of the secret data are images. A number of experiments are performed using images with different types and sizes for testing and evaluation of the proposed technique's efficiency. The typical copy of the original one is produced from decrypted data. The B-GET security evaluates based on key space, visual testing, histogram analysis, differential analysis, information entropy, correlation coefficient analysis and computational time. A. Key Space Analysis All initial parameters, keys, variables numbers, and their ranges combine the key space of B-GET. Most of them are floating-point numbers so; the proposed technique has excessively sufficient key space size. This key space size makes impractically brute force attack. A small change in initial parameter values will affect in the encryption direction and velocity. The pulse rate and loudness values also have large-scale initial values that increase key space size. In addition to arithmetic and logical operators, the crossover process and all combinations of them make good resistance against brute force attacks. B. Visual Testing A cryptosystem is secured if and only if it is necessary to know the complete information of the decryption algorithm to reveal hidden data. The B-GET is tested by using visual review. Grayscale images with size (256x256) and (1024x1024) pixels, and color images with size (256x256) and (512x512) pixels, as the sample of secret data, are shown in Fig.9. Fig.9. shows that there are absolute changes in the encrypted image with respect to its corresponding original image. original image original image original image original image image format image format image format image format (256x256 tiff) (512x512 tiff) (1024x1024 tiff) (256x256 jpg) Fig.9. Original images and their encrypted The gotten results prove that the encrypted image doesn’t keep any visual indication of its corresponding original image or any relation to it. Therefore, inspection with the naked eye does not detect or predict any information to discover secret data. C. Histogram Analysis The histogram displays the amount of pixels intensity values in the image in a graphical representation. For preventing an attack, the obtained cipher image shouldn’t provide any information about the secret image. A sample of different size gray and RGB images, their corresponding encrypted images and their histograms are shown in Fig.10. Original image Original image R Histogram Original image G Histogram Original image B Histogram Encrypted image Encrypted image R Histogram Encrypted image G Histogram Encrypted image B Histogram Original image Encrypted image Original image R Histogram Original image G Histogram Original image B Histogram Encrypted image R Histogram Encrypted image G Histogram Encrypted image B Histogram Original Gray Original Gray Encrypted image image Histogram Gray image Original Gray Original Gray Encrypted image Histogram image Gray image Encrypted Gray image Histogram Encrypted Gray image Histogram Fig.10. Original Image, Histogram of the original image, Encrypted Image and Histogram of the encrypted image The obtained histogram of cipher image by using the B-GET is significantly changed from the original one and the histograms of the encrypted images seem uniform. B-GET does not indict any evidence to secret data. D. Correlation Coefficient Analysis The correlation coefficient (CR) determines the relationship between the two data samples. If the value of the correlation coefficient is nearly equal zero, there is a weakly relationship between two data samples. Otherwise, the correlation coefficient is close to one if there is a strong relationship between the two data samples. The correlation coefficient is defined by the following formula [34]: CR SmSn(Imn-I)(Jmn-J) S m S n ( Imn-I ) ( J™"J ) where; I and J are the same size matrices or vectors. and are Average of I and J matrix elements respectively. The MATLAB function (corr2 (I, J)) is used to determine the relationship degree between original and encrypted images. The value of correlation coefficient is in - E. Information Entropy Analysis The information entropy is a numerical measure of randomness of given data. It can be used to describe the texture of the input grayscale image The Information entropy (Entropy) is defined by the following equation: Entropy= - SPi log 2 (Pi ) i=0 Where; Pi is the histogram counts. If the entropy value is nearly equal eight, there is more randomness in data, [35]. A sample of the secret images, their correspondent encrypted images and their entropy values are presented in Fig.11. All entropy values of the encrypted image are very close to eight. These entropy values prove that encrypted images are truly random and entropy attack is very difficult. Original image 6Sэдч Encrypted image Original image Encrypted image Original image Entropy Encrypted image Entropy Original image Entropy Encrypted mage Entrop R G B R G B R G B R G B 7.9993 7.9994 6.5449 7.9993 Fig.11. Entropy analysis of the original image and its correspondent encrypted image F. Structural Similarity Index Analysis Structural Similarity Index (SSIM) quantifies image features degradation that produced by processing. It is a metric which; measures the Structural difference between the original image and its processed one. SSIM is an image quality metric which; evaluates the visual impression of luminance, contrast, and structure of an image. The SSIM is used for perceptual quality evaluation. The value of SSIM equals one if two images are matching. The greater the difference between them, the smaller the value, MATLAB function (ssim) uses for computing SSIM value. The average of SIMM value between original and encrypted image approximately equals 0.0097 and its value between two encrypted images when changing only one pixel of the original image approximately equals about 0.0024. As inference, it appears that the values of the SSIM are too small, indicating the original and encrypted images are completely different and there is no correlation between them. G. Differential Attack In general, a common characteristic of an image encryption scheme is to be sensitive to minor modifications in the plain images. The differential analysis allows that an adversary is able to create small changes in the plain image and revise the encrypted image. The alternation level can be computed by means of two formulae, namely, the number of pixels change rate (NPCR) and the unified average changing intensity (UACI) [36]. H. NPCR and UACI Analysis A good encryption technique generally characterizes by its sensitivity for slight modifications in the secret data. The ability of resistance against differential attacks is confirmed by two parameters. The first is NPCR that measures the change rate of pixels in the encrypted image when changing only one pixel of the original image and defined as follows: NPCR (A, B ) = m x n ( ^ ^szm (i, j) x100% In addition, sim is represented by Equation: sim (i, j) if A (i, j ) = B (i, j) if A (i, j )* B (i, j) The other parameter is unified average changed intensity (UACI). UACI measures the percentage differences between the original intensity and encrypted image intensity that using the following Equation: UACI (A, B ) = m x n _ i. j A (i, j)- B (i, j) max_ pixel _ value ^x100% Where A, B are two encrypted images for the same original image with the only one-pixel difference in it, m and n are width and height of encrypted images, and max_pixel_value indicates the largest value in them [37, 38]. These parameters are used for testing the effect of changing of a single pixel in the original image on the encrypted image. They also used to test and verify its’ resistance to the differential attacks [39]. NPCR = 99.6098, UACI = 12.5431 Correlation = 0.0012 NPCR = 98.3101 UACI = 12.9883 Correlation = 0.0017 NPCR = 98.3101UACI = 12.9883 Correlation = 0.0017 NPCR = 98.3101 UACI = 12.9883 Correlation = 0.0017 Encrypted images Encrypted images (A) (B) (a) (b) Fig.12. Two encrypted images corresponding to Change one pixel in original image before encryption I. Processing Time The average of computation time needed to encrypt/decrypt secret data with different size and type are listed in Table 1 with a different number of iteration and number of Bats. Table 1. Average of Encrypt/Decrypt Computation Time Secret Data Size Format No. of Iteration No. of Bats Computation Time (Seconds) Encrypt Decrypt 256x256 tiff 3 12 0.0487 0.0363 5 7 0.0459 0.0334 2 7 0.0418 0.0314 512x512 gif 3 12 0.1367 0.1033 5 7 0.1348 0.0989 2 7 0.1279 0.0935 256x256x3 tiff 3 12 0.1308 0.0938 5 7 0.1411 0.0923 2 7 0.1195 0.0882 512x512x3 jpg 3 12 0.3937 0.2925 5 7 0.4064 0.2944 2 7 0.3902 0.2805 The average of computation time required to encrypt message's text file is almost zero. Conversely, encryption of audio and video file takes longer time due to the relatively great size of data amount that must be needed each second to reproduce a digital audio or video signal. All encrypted data are similar to random data based on various metric measurements. According to empirical outcomes, the maximum processing time for encrypting (512x512) true color image is around ½ second, but, it is less than 0.2 second in gray. This paper proposed the B-GET to increase encryption efficiency based on the parameters of bat algorithm and genetic processes. B-GET is also included mixing of the arithmetic and logical operations, encryption keys and randomly bats movement for quality of the encryption. The results show the resistance of the B-GET technique against different attacks based on the operations order of B-GET and several parameters. Reconstructed data is matching copy of the original. According to the various metric measurements the encrypted data is considerable random and has given no indication of secret data so the cryptanalysis' opportunities for breaking the cipher are negligible. Furthermore, the proposed technique is convenient for many applications where it achieves confidentiality, and data protection against revealing in acceptable time. In future work, we will be parallelizing and optimizing B-GET to reduce the complex cost of encryption of audio and video and try to reduce encrypted data size. [29] Xingwang Huang, Xuewen Zeng and Rui Han, “Dynamic Inertia Weight Binary Bat Algorithm with Neighborhood Search”, Hindawi, Computational Intelligence and Neuroscience, Volume 2017, Article ID 3235720, 15 pages, 2017. [30] X. S. Yang, M. Karamanoglu, and S. Fong, "Bat algorithm for topology optimization in microelectronic applications", presented at the IEEE International Conference on Future Generation Communication Technology (FGCT2012) London, 2012. [31] Yang, X.-S., and He, X., (2013) ‘Bat Algorithm: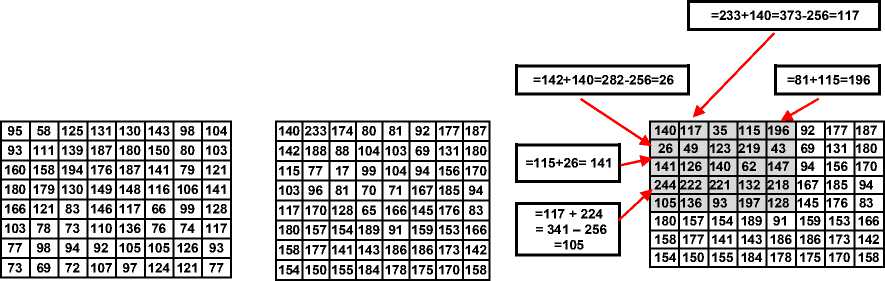
VI. Implementation and Evaluation Results






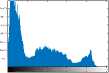

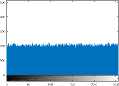
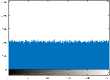
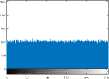

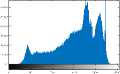
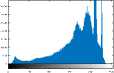


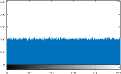
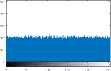





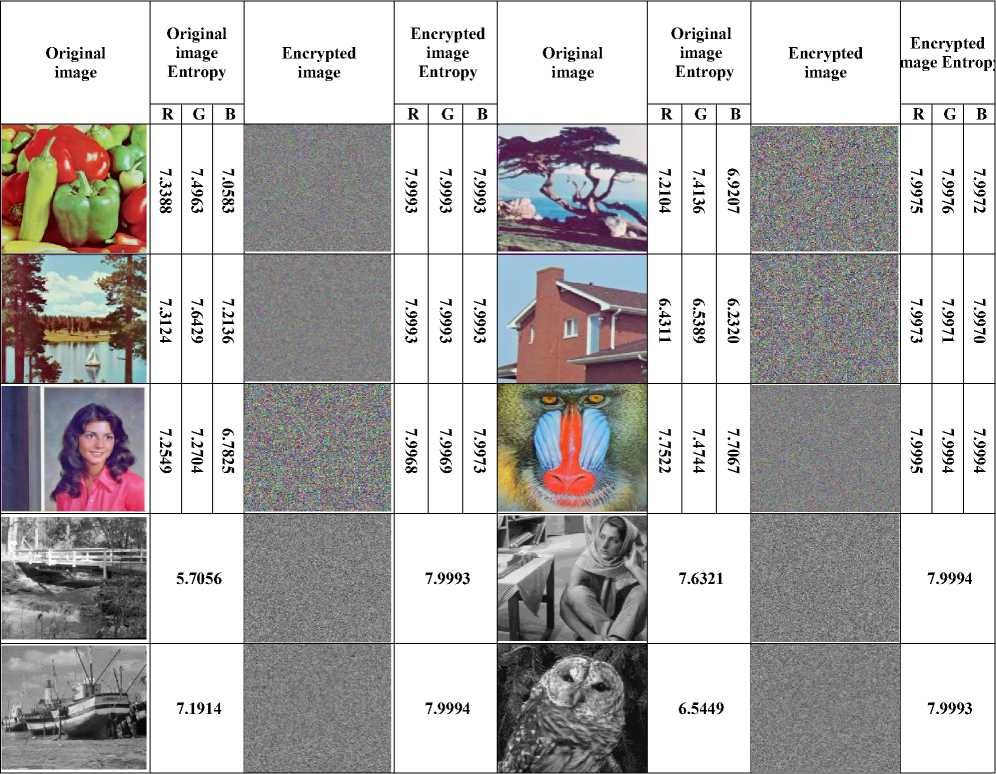



VII. Conclusions
Список литературы Bat-Genetic Encryption Technique
- William Stallings, "Cryptography and Network Security: Principles and Practice", Prentice Hall, 2011.
- Jonathan Katz and Yehuda Lindell, “Introduction to Modern Cryptography”, CRC Press, Taylor & Francis Group, 2nd Edition, LLC, 2015.
- Mark Rhodes-Ousley, “The Complete Reference Information Security”, The McGraw-Hill Companies, Second Edition, 2013.
- Zaidoon Kh. AL-Ani, A. A. Zaidan, B. B. Zaidan and Hamdan.O.Alanazi, "Overview: Main Fundamentals for Steganography", Journal of Computing, Vol. 2, Issue 3, pp. 158-165, March 2010.
- Mark Stamp and Richard M. Low, “Applied Cryptanalysis Breaking Ciphers in the Real World”, John Wiley & Sons, Inc., Hoboken, New Jersey, 2007.
- Dana S. Leaman, “Cryptographic and Security Testing”, National Voluntary Laboratory, Accreditation Program Standards Coordination Office, NIST HANDBOOK 150-17, 2012 Edition.
- B. Schneier, “Applied Cryptography”, John Wiley & Sons, New York, 1994.
- Ritu Goyal and Mehak Khurana, "New Design of Tiny-Block Hybridization in AES", International Journal of Computer Network and Information Security (IJCNIS), Vol. 9, No. 9, pp. 46-53, 2017. DOI: 10.5815/ijcnis.2017.09.06
- Omar A. Dawood, Abdul Monem S. Rahma and Abdul Mohsen J. Abdul Hossen,"The New Block Cipher Design (Tigris Cipher)", IJCNIS, vol.7, no.12, pp.10-18, 2015. DOI: 10.5815/ijcnis.2015.12.02.
- M. Mudia and Pallavi V. Chavan, “Fuzzy Logic Based Image Encryption for Confidential Data Transfer Using (2, 2) Secret Sharing Scheme”, Procedia Computer Science 78, pp. 632 – 639, 2016.
- K. Ganesh Kumarand D. Arivazhagan” New Cryptography Algorithm with Fuzzy Logic for Effective Data Communication”, Indian Journal of Science and Technology, Vol. 9(48), pp. 1-6, December 2016
- Gamil R.S. Qaid And Sanjay N. Talbar, “Encrypting Image By Using Fuzzy Logic Algorithm”, International Journal of Image Processing and Vision Sciences (IJIPVS), Vol. 2(1), pp. 25-29, 2013.
- Naveed Ahmed Azam, ”A Novel Fuzzy Encryption Technique Based on Multiple Right Translated AES Gray S-Boxes and Phase Embedding”, Security and Communication Networks, pp. 1-9 Volume 2017.
- Hamdy M. Mousa, “DNA-Genetic Encryption Technique”, I. J. Computer Network and Information Security, No. 7, pp. 1-9, 2016.
- Fatma E. Ibrahim, M. I. Moussa and H. M. Abdalkader, “A Symmetric Encryption Algorithm based on DNA Computing”, International Journal of Computer Applications (0975 – 8887) Volume 97– No.16, pp. 41-45, July 2014.
- Zhang, Q., Guo, L. and Wei, X., “Image encryption using DNA addition combining with chaotic maps”, Mathematical and Computer Modelling 52, pp. 2028-2035, 2010.
- Varuna S, Ramya R, ”An Integration of Binary Bat Algorithm and Naïve Bayes Classifier for Intrusion Detection in Distributed Environment”, International Journal of Advanced Research in Computer and Communication Engineering, Vol. 6, Issue 2, pp. 164-168, February 2017. DOI 10.17148/IJARCCE.2017.6237
- Fridrich, J., “Symmetric ciphers based on two-dimensional chaotic maps”, International Journal of Bifurcation and Chaos 8, pp. 1259–1284, 1998.
- Mao Y, Chen G, Lian S., “A novel fast image encryption scheme based on 3D chaotic Baker maps”, International Journal of Bifurcation and Chaos 14, pp. 3613–3624, 2004
- Liu H, Zhu Z, Jiang H, Wang B., “A Novel Image Encryption Algorithm Based on Improved 3D Chaotic Cat Map”, The 9th IEEE International Conference for Young Computer Scientists, pp. 3016-3021, 2008
- Hamdy M. Mousa, "Chaotic Genetic-fuzzy Encryption Technique", International Journal of Computer Network and Information Security (IJCNIS), Vol.10, No.4, pp.10-19, 2018. DOI: 10.5815/ijcnis.2018.04.02
- X.-S. Yang, “A new metaheuristic bat-inspired algorithm,” in Nature Inspired Cooperative Strategies for Optimization (NICSO2010), J. R. Gonzalez, D. A. Pelta, C. Cruz, G. Terrazas, and N. Krasnogor, Eds., vol. 284 of Studies in Computational Intelligence, pp. 65–74, Springer, Berlin, Germany, 2010.
- David A. Coley, “An Introduction To Genetic Algorithms For Scientists And Engineers”, World Scientific Publishing Co. Pte. Ltd, 1999.
- G. Wang, M. Lu, and X. Zhao, “An improved bat algorithm with variable neighborhood search for global optimization,” in Proceedings of the IEEE Congress on Evolutionary Computation (CEC ’16), pp.1773–1778, Vancouver, Canada, 2016.
- S. Yilmaz and E. U. K¨ uc¸¨ uksille, “A new modification approach on bat algorithm for solving optimization problems,” Applied Soft Computing, vol.28, pp. 259–275, 2015.
- Amir H. Gandomi and Xin-She Yang, “Chaotic bat algorithm”, Journal of Computational Science, Vol., 5, pp. 224–232, 2014.
- Komarasamy, G., and Wahi, A., “An optimized K-means clustering technique using bat algorithm”, European J. Scientific Research, Vol. 84, No. 2, pp.263-273, 2012.
- Kapil Sharma, Sanchi Girotra, "Parallel Bat Algorithm Using MapReduce Model", International Journal of Information Technology and Computer Science(IJITCS), Vol. 9, No. 11, pp. 72-78, 2017. DOI: 10.5815/ijitcs.2017.11.08
- Xingwang Huang, Xuewen Zeng and Rui Han, “Dynamic Inertia Weight Binary Bat Algorithm with Neighborhood Search”, Hindawi, Computational Intelligence and Neuroscience, Volume 2017, Article ID 3235720, 15 pages, 2017. https://doi.org/10.1155/2017/3235720.
- X. S. Yang, M. Karamanoglu, and S. Fong, "Bat algorithm for topology optimization in microelectronic applications", presented at the IEEE International Conference on Future Generation Communication Technology (FGCT2012) London, 2012.
- Yang, X.-S., and He, X., (2013) ‘Bat Algorithm: Literature review and applications’, Int. J. Bio-Inspired Computation, Vol. 5, No. 3, pp.141–149, 2013.
- V. Lakshmi Devi, P. Bharath Kumar and P. Sujatha, “A Hybrid BAT-GA Optimisation of Security Constrained Unit Commitment Problem for 10-unit System”, International Science Press, International Journal of Control Theory and Application, Vol. 10(5), pp. 823-830, 2017.
- David A. Coley, “An Introduction to Genetic Algorithms For Scientists and Engineers”, World Scientific Publishing Co. Pte. Ltd, 1999.
- Moore, D.S., “The basic practice of statistics”, W. H. Freeman and Company, New York, 2009.
- Robert M. Gray, Entropy and information theory, Springer-Verlag New York, Inc., New York, NY, 1990.
- Yue Wu, Joseph P. Noonan and Sos Agaian, “NPCR and UACI Randomness Tests for Image Encryption“, Cyber Journals: Multidisciplinary Journals in Science and Technology, Journal of Selected Areas in Telecommunications (JSAT), April Edition, 2011.
- Himan Khanzadi, Mohammad Eshghi and Shahram Etemadi Borujeni, ”Image Encryption Using Random Bit Sequence Based on Chaotic Maps”, Arabian Journal for Science and Engineering, Vol. 39, Issue 2, pp, 1039–1047, Feb. 2014. DOI 10.1007/s13369-013-0713-z
- Shrija Somaraj and Mohammed Ali Hussain, “Performance and Security Analysis for Image Encryption using Key Image”,Indian Journal of Science and Technology, Vol. 8 (35), Dec., 2015. DOI: 10.17485/ijst/2015/v8i35/73141.
- Narendra K Pareek, “Design and Analysis of a Novel Digital Image Encryption Scheme”, International Journal of Network Security & Its Applications (IJNSA), Vol.4, No.2, pp.95-108, March 2012. DOI: 10.5121/ijnsa.2012.4207


