Ba’zi bir xosmas integrallarni Eyler integrallari yordamida hisoblash

KIRISH

Quyidagi ishlarda ham fanlararo integratsiya katta ahamiyat qaratilgan.[1],[2],[7],[22] ishlarda matematika va informatika fanlari orasidagi fanlararo integratsiyaga katta e’tibor qaratilgan. [3],[4],[5],[6] ishlarda algebra va geometriya fanlari orasidai integratsiya misollar yordamida ko’rsatilgan. [8],[9],[10],[11],[12],[13],[14],[15],[16],[17],[18],[19],     [20],[21] ishlarda matematika, mexanika va fizika fanlari orasida integratsiyalarni ko’rsatib o’tilgan.

Tadqiqot ob’ekti va qo‘llaniladigan metodlar

Tadqiqot ob’ekti sifatida xosmas integrallarni Eyler integrallari yordamida yechish. Tadqiqot metodlari: masalani yechishning aniq usullari, taqribiy-aniq usullari va sonli usullari.

Olingan natijalar va ularning tahlili

Eyler integralari haqida teorima va xossalarida foydalanib xosmas integrallarni yechishni keltiramiz. Betta va Gamma funksiya haqidagi tushunchalarni keltirib o’tamiz.

Ushbu jxa-1(1 - x)b-1 dx         (a > 0, b > 0)                            (1)

xosmas integral Betta funksiya yoki 1-tur Eyler integrali deyiladi va B ( a , b ) kabi belgilanadi, ya’ni

B ( a , b ) = j x^{a - 1}(1 - x ) ^{b - 1} dx .                                         (2)

Integral ostidagi funksiya uchun:

• 1)    a <  0, b >  0 bo’lganda x = 0 nuqta;

• 2)    a >  1, b <  1 bo’lganda x = 1 nuqta;

• 3)    a <  1, b <  1 bo’lganda x = 0 va x = 1 nuqtalar maxsus nuqtalar bo’ladi.

Demak, (1) integral parametrga bog’liq bo’lgan xosmas integraldir.

Betta funksiya quyidagi xossalarga ega.

1-xossa. (1) integral

M = {(a; b) e R2 : a e (0;+®), b e (0;+®)} to’plamda yaqinlashuvchi.

2-XOSSa. (1) integral M_o = {( a ; b ) e R ² : a e [ a ₀;+® ), b e [ b ₀; +® )}, a ₀ >  0, b >  0 to’plamda tekis yaqinlashuvchi, lekin M to’plamda esa notekis yaqinlashuvchi.

3-xossa. B ( a , b ) funksiya M to’plamda uzluksiz funksiyadir.

4-xossa. V ( a , b ) e M uchun B ( a , b ) = B ( b , a ) (simmetrik) bo’ladi.

5-xossa. B ( a , b ) funksiya quyidagicha ham ifodalanadi:

+® a- - 1

B ( a , b ) =     ----- ddt

• ^{,       J}_o (1 + 1 ) a ^{+ b}

Isbot:

x

----= t

• 1    — x

x = t - tx

B ( a ; b ) = j x'

a

-

¹ • (1 — x ) ^{b — 1} dx =

®

a — 1

b - 1

•

x + tx = t

x • (1 + t ) = t

t x =

1 + 1

—

- ®      t^{a — 1}

^j (1 + 1 ) ^{a + b — 2 + 2}

dt

(1 + 1 ) ²

® j 0

v ® t a 1

dt " j (1 + 1 ) a ^{+ b}

t +1 — t        dt dx =------7- dt =------г

(1 + 1 ) 2        (1 + 1 )²

t 1

1 + 1

1 - x = 1 -

1 + 1

a - 1

•

(1 + 1 ) a ^{— 1} ( t + 1 ) ^{b — 1}

dt .

•

dt

(1 + 1 ) ²

xossa isbotlandi.

6-xossa. V ( a , b ) e M_x = {( a , b ) e R ² : a e (0; +® ), b e (1; +® ) uchun b-\        ,   .

B ( a , b ) =-- B ( a , b — 1)

a + b — 1

a = 1 bo’lganda,

7-xossa.   B(a,1 — a) = —n— (0 < a < 1), xususiy holda sin an

B = | 1,¹ | = П 1 2 2 J

Gamma funksiya va uning xossalari.

Ushbu

J x a -1 e - x dx              ( a >  0)                                            (3)

xosmas integral Gamma funksiya yoki 2-tur Eyler integrali deyiladi va quyidagicha belgilanadi, yani

Г ( a ) = J x a ^{- 1} e - x dx        (a >  0)                                              (4)

Integral ostidagi funksiya uchun:

• 1)     a <  1 bo’lganda x = 0 nuqta maxsus nuqta;

• 2)     a >  1 bo’lganda (3) integral yaqinlashuchi;

• 3)     a <  0 bo’lganda (3) integral uzoqlashuvchi;

Gamma funksiya quydagi xossalarga ega.

1- xossa.

Г ( a ) = lim n^{a    1} ' ² ' ³ —⁽ n - 1)   .                                        (5)

ⁿ ^“    a ( a = 1) ■■' ( a + n + 1)

• (5 ) formula Eyler-Gauss formulasi deyiladi.

2-xossa. (3) integral Va e [a0, b0 ] (0 < a0 < b0 < +да) oraliqda tekis yaqinlashuvchi, a e (0,+«) da esa notekis yaqinlashuvchi.

3-xossa.  Г(a) funsiya  (0;+да) oraliqda uzluksiz va barcha tartibdagi uzluksiz hosilalarga ega, ya’ni

Г⁽ⁿ ) ( a ) = J x^a - ¹ e x (In x ) ⁿ dx ( n e N ).

4-xossa. Г ( a + 1) = aГ ( a ) ( a >  0).

5-xossa. Г ( n + 1) = n !

Г ( a ) Г ( b )

6-xossa. В ( a , b ) =           .

Г ( a + b )

7xossa. Г ( a ) Г (1 - a ) = В ( a ,1 - a ) = —^П —,   0 <  a <  1.

sin a n

L   (2 n - 1)!!

8-XOssa. Г ( n + -) = -— n^ n e N .

h Пл

9-xossa. Lejandr formulasi: Г ( a ) Г ( a + -) = ^ 0 - 1 Г (2 a ).

1-misol. Eyler integralidan foydalanib quydagi xosmas integralni hisoblang.

• 2     _dx

’3/ x ² (2 - x )

Yechilishi. Bu integralda

—x— = t almashtirish orqali quyidagi integralni 2 - x hosil       qilin,       keyin

uning

qiymatini

hisoblaymiz.

x

9           t ,

2 - x x = 21 - tx, x • (1 +1) = 21

2t x =---

1 + 1

dx =

2 • (1 + 1 )л       2 j

------dt =-----у dt

(1 + t ) 2        (1 + t )²

^

CO

I

___________2 dt ____________ °

J

(1 + 1 )² • з к— )² • (2 - —)    0 (1 + 1 )² •

1 + 1         1 + 1

3 •

2 dt

4 t ²     2

•

V (1 + 1 ) 2 1 + 1

- 2

= J-----^^---- у = [ qisqartirishlarni ama

0 (1 + 1 ) ² • —  • 1 3

t + 1

°

° A

- 2 - 3

°    3         ° t

1g a oshirib ] = J dt = J

0 ^{1 +} t      0 1 ⁺ t

- dt =

_ ° t ^{3 1} о ( 1 + 1 ) 3 ⁺ 3

12                                пп dt = B( ;—) = [Betta funksiyanmg 7 -xossasiga asosan] ==

33                                      sinпк

2 п

°

2-misol. Ushbu   J x ⁴ • e - ^{x 2} dx xosmas integralni Eyler integrali yordamida

hisoblang.

Yechilishi. Bu integralda x ² = t almashtirish orqali quyidagi integralni hosil qilamiz va qiymatini hisoblaymiz.

x2 = t, x ^ 0 da t ^ 0, x ^ ° da t ^ ° x = 4t

dt dx = —^

2t x4 = t2

^

°

J t

• e

- 1

° 3

2 Л 2 J t

dt

° 5

e ~ ‘ dt = — J 1 2

-

^

• e - t dt = ¹ Г |

] = ¹ Г | 2 + ¹ | =

^J 2 I 2 J

= [Gamma funksiyaning 8 - xossasiga asosan

•

( 2 • 2 - 1 ) !!

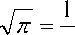
3!!

• yin =

3-misol. Eyler integrallaridan foydalanib, integralni hisoblang.

п j sin 4 x cos6 xdx =

sin x =

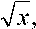
x = arcsin

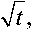
dt

dx =

1—4: ■ 2 —t

x —— 0 da t —— 0

п x —— — da t —— 1

13       5

= [ soddalashtiramiz ] = — j t ² • (1 - 1 )² dt = 2

2 j ^t

i + 3 - i

= j 1 ²(1 - 1 )³

dt

1— • 2 4t

i + 5 - i         1 1 5 - i           7 - i

• (i - 1 ) ² dt =ⁱJ t ²   • (i - 1 )² dt =

5      7           5      7               11

Г (5) • Г (7)   1 Г (5) • Г (7)  1 Г (2 + ^А) • Г (3 + ^А)

= - B (-;-) = -4—=2- = - • —2----2- = -22- =

2 2   2      5  7     2     Г (6)      25!

(2• 2-1)!! r (2• 3-1)!!  r      3!! r 5!! r i     2     п     2     ^п 1  4 • п • 8 • ^П 1 • 3 •i• 3 • 5 • п 3п3

—--=---=----------=---=--

2                5!                 2        120            64 ^120      64 • 8512

Xulosa qilib aytganda o’quvchi talabalar ba’zi bir xosmas integrallarni yechishda qiyinchiliklarga duch keladi. Shunga uxshash qiyinchiliklarni bartaraf etish uchun Eyler integrallaridan foydalanib xosmas integrallarni yechish o’quvchi talablarga ancha qulayliklar keltiradi.

Foydalanilgan adabiyotlar:

"Экономика и социум" №8(87) 2021