Behavioral Compatibility Analysis of Component-based Real-time System

Component-based programming and component-based system construction have emerged as important topics in software engineering, as witnessed by the number of recent papers addressing these themes in the sub fields of software architecture (e.g.[1,2,3,4,5,6]), software configuration management (see e.g.[7,8]), and standardized component models such as OMG’s CCM, Sun’s EJB, or Microsoft COM[9,10]. However, little is still known about the behavioral compatibility of real-time system.

In real-time system, the total correctness of an operation depends not only upon its logical correctness, but also upon the time in which it is performed, therefore time property is crucial for the component composition. The behavioral incompatibility of real-time system is often due to the inconsistency of clock constraints. So, how to describe and verify such behavioral incompatibility in an effective way should be taken more into consideration in real-time system component composition.

Thesis [11] uses Hierarchical Timed Automata (HTA) [12] to describe component and use Multiset Labeled Transition Systems (MLTS) to represent the interface actions of HTA to perform composition

* Corresponding author.

E-mail address:

verification, but this analysis technique need transform every component’s HTA model to a MLTS manually, which can not be claimed to be of practical value.

Our work is based on existing efficient and well proven symbolic analysis techniques of Timed Automata (TA) [13,14], which will be briefly introduced in Section II. According to the character of component-based software development, this paper makes use of TA to describe the component and the whole system, which will be briefly introduced in Section Ш. Section W presents our proposal on component behavioral compatibility. We specify the component behavior using a deterministic and output urgent class of UPPAAL [15] style timed automata, then the problem of component behavioral compatibility equivalent to whether the complementary actions can really synchronize over common channels[15] on the system’s TA model. We enable formulation of the behavioral compatibility verification as reachability properties that can be checked by reachability analysis of the model, then use the verification function of the UPPAAL tool to generate the result. In Section V, we apply our method to the composition of the railway level crossing control system. Our results demonstrate the effectiveness and performance of our proposal. Finally, Section И concludes this paper.

• 2.    Timed automata

• 3.    Ta model of real-time system component

In this section, we will give a brief introduction of the background-timed automata, which will be helpful for future work.

Let X be a set of non-negative real-valued variables called clocks, the set Φ(X) of clock constraints δ is defined inductively by б:= x<=c | c<=x | -б | 6 1 Л6 2 ,where x is a clock in X and c is a constant. A clock interpretation v for a set X of clocks assigns a real value to each clock; that means, it is a mapping from X to R. We say that a clock interpretation v for X satisfies a clock constraint δ over X iff δ evaluates to true using the values given by v. A timed automaton (TA) is a tuple <Σ,L,L 0 ,X,I,E>,where Σ is a finite alphabet, L is a finite set of locations, L 0 — L is a set of start locations, X is a finite set of clocks, I is a set of invariant, and E — L×L×Σ×2^X×Φ(X) gives the set of transitions. I assigns clock constraint to every location l, that is, it is a mapping from L to Φ(X). An edge represents a transition from location l to location l` on input symbol a. The set x ^— X gives the clocks to be reset with this transition, and б is a clock constraint over X.

The semantics of a TA is defined in terms of a timed transition system over states of the form s= (l,v), where l is a location and v is a clock valuation satisfying the invariant of I. Intuitively, there are two kinds of transitions: delay transitions and discrete transitions. In delay transitions, (l,v) — —• (l,v+d), the values of all clocks of the automaton are incremented with the amount of the delay, d. Discrete transitions (l,v) ——• (l`,v`) correspond to execution of edges for which the guard δ is satisfied by v. The clock valuation v` of the target state is obtained by modifying v according to update λ. So, for the timed transition system, the transition label can be a E S or d E R⁺. A timed trace is a sequence of alternating time delays and symbols in S.

We adopt TA model to describe formally the system and its components.

Component is a computation or logical unit with a certain function which is made up of component interface and implementation. Component interface includes a set of interaction operations between components and external environment, and the description of components' dynamic behavior. While component implementation implements the component interface behavior.

Timed automata model of component P could be described as a quintuple as follows:

P , A_P^I , A_P , A_P^H , B_P>

In which:

• 1)    ID_P refers to component P;

• 2)    A^I 、 A^O 、 A^H are three sets mutually exclusive, which correspondingly refer to the input operation set, the output operation set, and the internal operation set of component P. Therein, the input operation set includes methods invoked or information received over the communication channel; the output operation set comprises methods of external environment invoked or the information sent to the communication channel; and internal operation set consists of the exchange of internal information, not visible to the outside.

• 4.    Component behavioral compatibility analysis

• 4.1.    Incompatible Component Behavior

• 4.2.    Component Behavioral Compatibility Verification

B P describes the action semantics and dynamic behaviour of component P. To the component itself, it is a TA <Σ,L,L 0 ,X,I,E> .

If the function of the system could be implemented by the composition of component P 1 , P 2 ,……P n , the system model can be regarded as the network of the corresponding components’ TA models. A network of TA A 1 ‖ … ‖ A n over (Σ,X) is defined as the parallel composition of n TA over (Σ,X).

Software systems are typically made out of numerous components whose behavior is individually well known. Thus, the main problem faced by a software designer is that of understanding whether the components fit together well [2]. Adequate techniques are hoped to prove the well formedness of the system or to single out the components responsible for behavioral mismatches.

Component composition is to coordinate different components’ behavior and turn them into an organic whole. It requires not only the match of parameter declared in the component interface, but also the compatibility of the component behavior because there may be inconsistency action.

Components behavior is incompatible when one component generates an output action, but the other component is not prepared to accept it, i.e. the matching input action of the other component is not enabled, or vice versa. That is to say, in the TA model of the system, which is assembled by components P and Q, there is a channel a, a! ∈ A^O ∧ a? ^∉ A^I or a! ∈ A^O ∧ a? ^∉ A^I . The inconsistency of clock constraints often results in behavioral incompatibility for real-time system.

A network of TA A 1 ‖ … ‖ A n over (Σ,X) is defined as the parallel composition of n TA over (Σ,X). Semantically, a network again describes a timed transition system obtained from those of the components by requiring synchrony on delay transitions and requiring discrete transitions to synchronize on complementary actions (i.e. a? is complementary to a!, a! ∈ A^O ∧ a? ∈ A^I ). So, the problem of component behavioral compatibility equivalent to whether the complementary actions can really synchronize over common channels on the system’s TA models.

We use model checking for verification. Here, we explain how component behavioral compatibility problem can be computed using reachability analysis, effectively giving automated tool support.

UPPAAL is a verification tool for a TA based modeling language. Besides dense clocks, the tool supports both simple and complex data types like bounded integers and arrays as well as synchronization via shared variables and actions. The specification language supports safety, liveness, deadlock, and response properties. UPPAAL supports synchronization, processes can synchronize over channels and edges labelled with complementary actions over a common channel synchronize.

• 1)    Action synchronization rule

Action synchronization rule: The Action synchronization rule is a technique where the idea is to ensure that all complementary actions can really synchronize.

There must be component behavioral incompatibility for component-based system if it does not satisfy the Action synchronization rule.

To verify component behavioral compatibility, we assume that the edges of a model are enumerated, so that e i is the number of edge.

We use (a, e_i , e j ) to denote an action synchronization pair (AS-pair) for channel a if e_i is an edge where a! is defined and e j is an edge where a? is defined. An AS-pair (a, e_i,e j ) is valid if complementary actions in e_i and e j can really synchronize. A component-based system satisfies the Action synchronization rule if for all channels, all AS-pairs are valid. Attention, there may be more than one edge where a! or a? is defined, so all complementary action combinations should be taken into consideration.

In the real-world many system behave non-deterministically and synchronizely. In UPPAAL, system can be modeled as a collection of non-deterministic processes with finite control structure and real-valued clocks (i.e. timed automata), communicating through channels and (or) shared data structures. So our definition above is suitable and the model checking tool-UPPAAL is appropriate for such systems.

Throughout the paper we use UPPAAL syntax to illustrate TA, and the figures are direct exports from UPPAAL. Initial locations are marked using a double circle. Edges are by convention labeled by the triple: guard, action, and assignment in that order. Committed locations are indicated by a location with an encircled “C”. A committed location must be left immediately as the next transition taken by the system. Finally, clock conditions placed under locations are location invariants.

• 2)    Verification of AS-pair validation

• 5.    Case study

Whether an AS-pair (a, e_i , e j ) is valid can be verified in the following way: add an auxiliary array of type Boolean (initially false) for edges in AS-pairs (typically realized as a bit array in UPPAAL), and add to the assignments of each edge e i an assignment array[i]:=true; the problem of whether an AS-pair (a, e i , e j ) is valid can be formulated as a reachability property requiring that all edge variables in AS-pair are true: E<> (array[i]= =true and array[j] = = true).

The auxiliary array is needed to enable formulation of the validation verification as a reachability property using the UPPAAL property specification language which is a restricted subset of CTL.

The reachability property will then require all representing valid AS-pairs to be true for the Action synchronization rule.

We assemble a simplified version of a railway level crossing control system as an example to demonstrate how our technique works.

The system is defined as rain, Turnout, Controller and Queue. It should obey the following rules:

• •    The turnout is a critical shared resource that may be accessed only by one train at a time;

• •    When approaching, an approach signal and the track id shall be given to inform which track it will be reaching; After a train passes through a turnout, an exit signal shall be sent to the controller;

• •    After a train gives an approach signal, the controller will check whether the turnout has been used. If the turnout is being used, an stop signal shall be given and the train is supposed to wait; otherwise, the controller will send a switch signal to the turnout, and send a go signal to the train within 10 time units;

• •    A turnout can be located at anywhere allowable. The switch shall be performed less than 10 time units after the turnout receives the switch signal turn from the controller;

• •    A train shall pass through a turnout within 5 time units, after which an exit signal shall be given. After the controller receives the signal, if there is a waiting train, it will send a correct switch signal, and send a go signal to the waiting train within 10 time units; otherwise, the controller will revert to the idle condition.

We select components Train, Turnout, Controller and Queue from our component library.

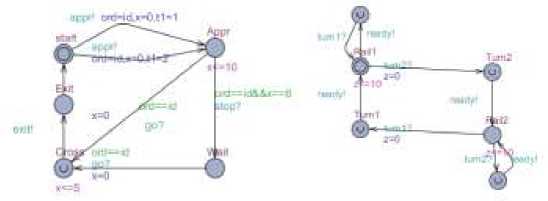
Fig. 1                                 Fig. 2

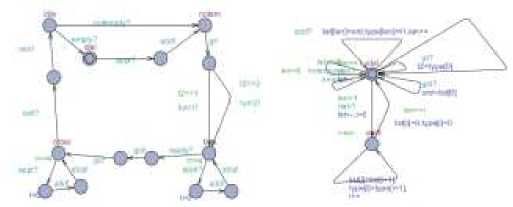
Fig. 3                               Fig. 4

Fig. 1-4 illustrates their TA models respectively.

The TA models above show there are 14 channels in the system: appr, go, exit, stop, turn, ready, turn1, turn2, add, rem, empty, notempty, gt, gid.

The verifier of UPPAAL is to check properties by on-the-fly exploration of the state-space of a system in terms of symbolic states represented by constraints, so it can be used on sizeable systems. All AS-pairs for 14 channels are verified and invalid AS-pairs have been found as (stop, e 23 , e 3 ) and (stop, e 29 , e 3 ), in which e 23 and e₂₉ denote the edges where stop! are defined, e₃ is the edge where stop? is defined, stop! ∈ A ^O and stop? ∈ A ^I . This means that the two components Train and Controller are behavioral incompatible and the system assembled by above components do not satisfy the Action synchronization rule.

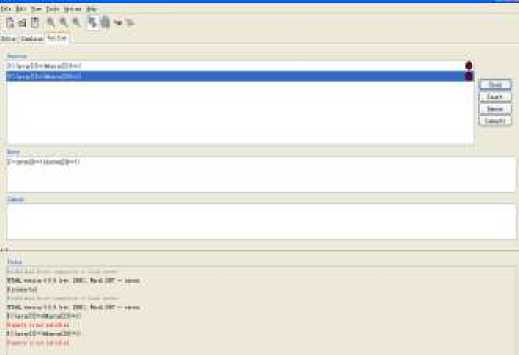
Fig. 5 displays part view of the verification and it can be obtained from the verifier of UPPAAL.

• 6.    Conclusion

In this paper, we have analyzed the component-based real-time system behavioral compatibility and proposed a method to enable formulation of the behavioral compatibility verification as reachability properties that can be checked by reachability analysis of the model, then use the verification function of the UPPAAL tool to generate the result. our work can be concluded to have the following features:

• 1)    The TA model of the component, which is explicit and not ambiguities, can offer detailed but not redundant information for component composition.

2 ) We need only construct every component’s TA models, the assembled system, which is the product of these TA models, can be constructed automatically by UPPAAL.

3 ) Behavioral compatibility verification is enabled as reachability properties that can be checked by UPPAAL. Model checking is often hampered by various state explosion problems. In UPPAAL these problems are dealt with by a combination of on-the-fly verification together with a new and coarser symbolic technique reducing the verification problem to that of solving simple linear constraint systems [15]. So our method is useful in sizeable component-composition systems.

Manually formulating the associated reachability property for AS-pairs is tedious and error prone. In future work we intend to develop a tool to perform these tasks automatically. Further more, an algorithm to behavioral compatibility verification are left to be developed and improved.