BER Analysis of OFDM Digital Communication Systems with Improved ICI Cancellation Technique
Автор: Sanjiv Kumar
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 4 vol.6, 2014 года.
Бесплатный доступ
In this paper, performance of OFDM digital communication systems have been analyzed with improved ICI cancellation technique. The bit error rate has been regarded as a fundamental information theoretic measure of a communication system. A novel parallel ICI cancellation technique has been proposed for mitigating frequency offset of OFDM digital communication systems. The simulated results of the proposed technique is compared with ICI self cancellation scheme. The simulated results show better performance over ICI self cancellation scheme.
Orthogonal Frequency Division Multiplexing, Inter Carrier Interference, Bit Error Rate, Self Cancellation Scheme
Короткий адрес: https://sciup.org/15010549
IDR: 15010549
Текст научной статьи BER Analysis of OFDM Digital Communication Systems with Improved ICI Cancellation Technique
Published Online March 2014 in MECS
Orthogonal frequency division multiplexing (OFDM) is a multicarrier modulation technique, which is widely used in various communication systems and standards due to its high data rate, high spectral efficiency and robustness to the frequency selective channels [1-3]. However, it is susceptible to the phase-noise and multicarrier frequency offset between the transmitter and receiver local oscillator, which causes several impairments including disrupting the orthogonality among subcarriers and introduces inter-carrier interference (ICI) that would significantly degrade the system performance [2-3]. The ICI is introduced by carrier frequency offset, phase noise and timing offset. The carrier frequency offset is caused by the mismatch of frequencies between the oscillators at the transmitter and receiver, or from the Doppler spread due to the relative movement between the transmitter and receiver [3]. The phase noise arises predominantly due to imperfections of the local oscillator in the transceiver. Essentially, it represents a time-varying drift of the local oscillator phase from its reference [4]. The timing offset arises due to the multipath delay spread and because of timing offset not only inter-symbol interference (caused by the next symbol), but ICI also occur . However, ICI induced by phase noise and timing offset can completely be compensated or corrected. Since the Doppler spread or frequency shift is random, hence we can only mitigate its impact. Li et al [5] have proposed a time-domain windowing approach for ICI mitigation. However, the time domain windowing should be implemented after cyclic extension of the frame, so that the windowed frame is not cyclically extended. It can only reduce sensitivity of only time offset, which is not the major source of ICI and also reduces bandwidth efficiency. A simple and most effective method, called the self-cancellation scheme has been proposed by Zhao and Haggman [6], which significantly reduces the ICI with little additional computational complexity. This scheme significantly reduces the ICI at cost of reducing the transmission rate. Besides its low computational complexity, another very important advantage of the self-cancellation scheme is that it can also be useful to mitigate the ICI created by a spread of frequency shifts in the signal such as a Doppler spread resulting from a time variable channel. The main idea is to modulate the input data symbol onto a group of subcarriers with predefined coefficients such that the generated ICI signals within that group cancel each other, hence the name self-cancellation. In this ICI mitigation technique, the bandwidth efficiency becomes half, which is the major drawback of this technique. The frequency offset estimation and compensation techniques [6], correlative coding [7] and the conjugate cancellation scheme [11] are some other techniques to cancel ICI. Zhao et al [7] have proposed the correlative coding between the signals modulated on subsequent subcarriers in binary phase-shift keying OFDM but this scheme does not improves carrier-to-interference ratio (CIR) significantly. In the conjugate cancellation scheme, which is proposed in [11], two sequences are transmitted in each data symbol. First sequence is original received sequence and another sequence is conjugate of the original sequence. Thus the two sequences are conjugate of each other rather than adjacent subcarriers with opposite polarities in order to cancel the ICI. In [20], the bit-error-rate (BER) upper bound of the OFDM system is analyzed without ICI self-cancellation where as in [21], it is analyzed by using self-cancellation technique but this method is less accurate. Yeh et al [22] have discussed the ICI mitigation technique using conjugate-cancellation but they have not provided any mathematical analysis for the calculation of ICI.
In this paper, an effort has been made for presenting the BER analysis and improved ICI cancellation technique for the OFDM digital communication systems. In the proposed technique, at the transmitter, IFFT is performed for first part of the data and FFT for the second part of data. At the receiver, FFT is performed for the first part of the data and IFFT for the second part of the data. These combined operation forms an ICI cancellation scheme for mitigating the frequency offset of the OFDM communication systems. The BER performance of proposed scheme is compared with self cancellation scheme for BPSK OFDM system and 16-QAM OFDM system. The CIR performance of proposed technique is compared with ICI self cancellation and standard OFDM schemes.
This paper discusses about error rate analysis of OFDM digital communication systems for the mitigation of inter-carrier interference in mobile environment. The rest of the paper is organized as follows. Section II discusses about the system model of OFDM digital communication system with proposed scheme. Section III deals with proposed ICI cancellation technique in OFDM digital communication system. In section IV, the analyzed and simulated proposed techniques are discussed. Finally, section V concludes the work.
-
II. Proposed System Model
Let us consider a typical discrete-time base band equivalent model of the OFDM digital communication system. The input binary serial data stream is encoded by using suitable modulation technique (M- QAM, BPSK, and QPSK). Then the symbols are transferred to the serial-to-parallel (S/P) converter and in this stage, duration of bits is increased. At the transmitter, the parallel bit stream is subjected to IFFT block and second part is subjected to FFT block. The modulated symbols are serialized using a parallel-to-serial (P/S) converter. Now, the guard band addition is performed because at the receiver, one OFDM symbol is overlapped with the other symbol due to the multipath distortion. To eliminate the problem of inter symbol interference a guard time inserted between two symbols and duration of the guard interval should be greater than the maximum delay spread. After this the digital signal is converted to analog via the digital-to-analog (D/A) converter before send down to the channel. At the receiver side, the guard interval is removed and the received symbol is converted from analog-to-digital by using the analog-to-digital (A/D) converter. In the next part, the data is transferred to the serial-to-parallel (S/P) converter and then data is sent in IFFT and FFT block. After FFT and IFFT block data is sent for parallel-to-serial conversion and then for demodulation. The ICI cancellation is performed after demodulation by using the diversity combiner.
-
III. Proposed ICI Cancellation Technique
The input data bits are encoded by using suitable modulation technique like (QPSK or QAM) and the output of this block is Xk . t he ifft output at transmitter is given by [8]:
x n — N f ' X k e 2 * n
N k = 0
n = 0, ', 2,...,N-'.
Where N > 2k + ' , and k is the number of subcarriers and N is the period of IFFT. The frequency offset arises due to the frequency mismatch of oscillator of the transmitter and receiver as discussed in [8]. At the received sequence after passing through the channel can be expressed as:
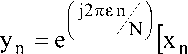
* h n ]+ W n
Where h is channel impulse response, W is additive white Gaussian noise (AWGN) and 8 is normalized frequency offset. The normalized frequency offset is constant over the one IFFT period as discussed in [8]. Due to the ICI, the performance of OFDM communication system is decreases greatly. After some mathematical manipulation (2), can be expressed as:
yn nN
" f ' XkHke2 n jn 1 k +s )lN k — 0
+ Wn
Where Hk is the channel transfer function at the frequency of kth subcarrier? The output of DFT demodulator can be expressed as:
Yk =f n—0
N
k — 0
Y k = (X k H k W
2 n jn | k + ^ )
N
- 2 n jkn
+ W r e
sin П8
\ N ( ле /N )
l ej . |N - ')/N + I k (4)
The first component on the right-hand side of (4) is the modulation value Xk which is modified by channel transfer function. This component experiences an amplitude reduction and phase shift due to the frequency offset. The second term is the ICI term, which arises due to frequency mismatch of the oscillator transmitter and receiver. So the ICI can be expressed as:
N - 1 n - 1 2 n jn ( l +£— k )
Ik = Z TF XH Z e N
I = 0 N n = 0
I * k
The summation term in (5) is the geometric progression of total N terms with common factor is exp (2 П ( l + £ — k )). The expansion of summation factor is as below:
N — 1
Ik = Z - XH
I = 0 N
1 + e 2n j ((I+8-к)/N)
+e 4nj ((I+8—k)/N)+
+e 2nj (N—1)( (l+8—k)/N)
After addition of the above geometric progression, we get:
N—1 i 1-e2*j (l+8-k)
Ik = xHHl
k IZ0 N l l [1 — e2Пj((l+8—k)/N)
P
Bracketed term is taken as P for simplicity and simplified as:
( Sin^i+£-k) ) .n(((l+£—k)/N)Л p sin n (1 I о rv) e v sin n ((l + £ — k)/ N )7 e ~nj (l+£—k)
V 7
So now (5) can be written as:
N — 1
x' k = Z X k e "( 2 " jnk N )
n = 0
and
N — 1
Ik = Z NXHl l=0 N l ^ k
sin n(l +8— k )
f l +8— k j n( N — 1 ) | e V N
y ' k =
f 2 n jn ( — k +£ )
N—1 l----N----
Z XkHke V N
n=0
+ Wn
f l +8— k sin n|
V N
The sequence S ( l — k ) is defined as the ICI coefficient between l th and k th sub-carriers, which can be expressed as [6] :
S(l — k) =
sin( n (l — k + 8 ))
. f n (l — k + 8 )
Nsin
V N
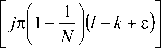
k = 0, 1, 2,......,N — 1.
The output of the IDFT demodulator can be expressed as:
, i N—1
Yk =- Z k Nk = 0
f 2 n jn( — k +8 )
N — 1 I
Z HkXkeV N n=0
+ W'n
f 2 n jkn e V "N”
The first term in the right-hand side of (4) represent the desired signal. The second term is ICI component. As we know, if £ becomes larger, the desired part |S (0)| decreases and the undesired part S ( l — k )| increases. S''(l — k) is ICI coefficient of the selfcancellation technique and given by (10) of [6]. S ' ( l — k ) is the proposed ICI coefficient. The data duplication is necessary for the ICI cancellation as discussed in [6, 9, 11]. The bandwidth efficiency is reduced due to duplication of data but it is comparable with the other ICI cancellation techniques as in [6, 11, 20-21].
Yk = (XkHk)
j n£ (N — 1) ]
N J+ ,k f'0)
II
, N-1
Ik = S -X/Я/S
/=0 Nn
N
Above summation term is in geometric progression of total N terms of common factor are exp ( 2 п (/ - £ - k ) ) and expand summation factor as below:
, N -1 1
Ik = S - X/Я/
/ = 0 N
2 n j ( ( - / +£+ k )/ N ) 4 n j ( ( - / +£+ k )/ N ) j ( N - 1 )( ( - / +£+ k )/ N )
I e I e I I e or
, N -1 i 1-e2 n j ( - / + £ + k )
Ik = Z —H]H1 ------7----------гk /=0 N / [1 - e2nj((-/+£+k)/N)
P'
Bracketed term is taken as P' and it can be simplified as:
|
P = |
" 1 - e 2 n j ( ( k + £ - / ) ' 2 n j ( ( k +£- / )/ N ) k 1 e 7 |
Х |
^ e - nj ( k +£- / ) e - nj ( ( k + £ - / )/ N p - n j ( ( k + £ - / )/ N ) X e -П j ( k + £ - / ) k e 7 |
(12) |
W'n is also the additive white g aussian noise. i t is assumed to be zero without loss in generality in above discussion as shown in [11]. The ICI term at the output of the receiver is:
I k = k 2 k (13)
By substituting the value from (6) and (12) in (13), we get:
I' = 1 N-1 ei”(N-1 *+£- k)/N 1 X,H, • k 2 /=0
( sin n (/ + £ - k)'
+
Ik
^“
sin n (k + £ - / n ( k + £ - / )
Now, we have considered following two cases: Case 1: If / - k = even numbers, then
N - 1
pt _ 1 X 1 ^jn(N-1)((/+£-k)/N)p sin П£ k Zx
2 /=0
N - 1
_ _ 1 j n ( N - 1)(( / +£ - k )/ N )j^ sin n£
/ /
2 /=0
2£ к )2 - £ £
e can be neglected in
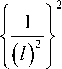
_ y1 gjn( N - 1)( ( / + £ - k )/ N ) j^ Ц sin n£ / = 0 / / П
_ _N ^1 ejn< N - 1) ( ( / + £ - k )/ N )^. Ц sin n£
/ = 1 / / n
£
£
/ # 0
For calculating the variance of ICI after cancellation, assume E(I k ) = 0 and average channel gain
E |H l|2 = |H2
is constant and E
X l2
= IXI2.
Here, / = 1 ......N-1, and N > 2K +1, so we can write -K ( / ( K . Also /^ is even function, (15) can be written as:
E [I I ■ r ]=l X r 'LE (IЯ/ 2}(^^n^F22 kj^rj
L J /=-к X n 7 [(/)
к X r HI1
sin П£Х £ j
I 2S n 7 /=1
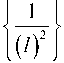
Now, I shall find variance of ICI:
The variance of ICI is:
а1С2 =| X|2 H 2 (sin ле х е ) 2 х 0.2195
Case 2: If l — k = odd numbers, then (14) can be written as:
|
у» 1 N ^1e j n ( N — 1) ( ( l + 8 — k )/ N ) sin ПЕ < k ll 2 l = 0 П ( _ 1 N — 1 j n ( N — 1)(( l + 8 — k )/ N ) v „ sin пе |
( ( l + 8 — k )J f |
+ |
f ( k + 8 — l ) J f-1-1 |
1 J 1 |
|
|
= T e l 2 l = 0 п = 1 N ^1 e jn ( N — 1) ( ( l +8 — k )/ N ) x H sin n8 . 2 l =0 1 1 | |
1 f |
l ( l + 8 — k ) J 2 8 ) |
— { |
l ( l — 8 — k ) J |
J |
|
l |
( l — k ) 2 — 8 2 J |
J |
|||
Since, l - k )} 8 so 8 can be neglected in compression of ( l — k ) 2 , so the above Equation can be expressed as:
Here, l = 1 ............N-1 and N > 2K +1, so we can write — K ( l { K . Also l^ is even function, (17) can be written as:
N — 1
~ ^ ^ я ( N — 1) ( ( l +8 — k )/ N ) X H l = 0
sin П8 n
IV
8 1
N — 1
~ у jn(N—1)((l+8—k)/N) X [[ ll l=0
sin П8
П
H(l — k )2 J J
[f 8 ^
H(l — k )2 J J
E 1 1 " I’ ]= 2 X Г it E { Hi1 { ^1 U l =1 \ п J l( l )
< 2 X |=£ e | H l | = Г^H ' l =1 \ п J l( l )
N — 1
— e j n (N — 1) ( ( l + 8 — k)/ N ) X H sin П8 X 8
l = 1 l l П
11(l )2 J
X2H2
№
2 E l = 1
l * 0
l(l)4 J
The variance of the ICI is:
Now, we find the variance of the ICI as:
EII" ki2 ]=i Xi2 TT E {HA l=1
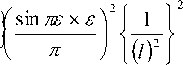
2 2 f sin П8 X 8 ]
l n J
IX 2 T EIHJ!
l =— K
sin ПЕ X 8
n J
1
------>
(l )2 J
The BER of QPSK OFDM system after ICI cancellation as given by:
X 2 H 2
2 X 2 H 2
{( sin П8 ) / П8 } / (1 + --——
BER = 1/2*Q
T^b- { ( sin П8 ) / П8 } / (1 + ^b- ( sin П8 X 8 ) X .2195)
-
IV. Results and Discussion
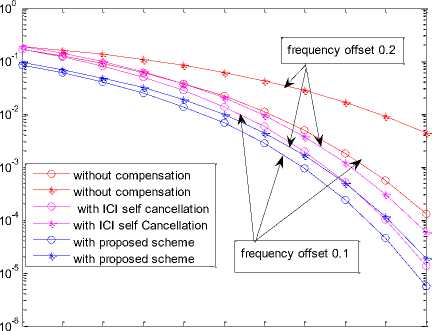
For minimizing the ICI in OFDM digital communication systems, an improved ICI cancellation technique is proposed. The simulations have been performed for the BPSK OFDM systems by using the proposed technique with N=64 and guard band seven. Fig. 1 shows comparison of BER between self cancellation scheme and proposed improved technique for the normalized frequency offset 8 = 0.1 and 0.2.
For the frequency offset 0.1, BER at 0dB SNR is greater than 10-1 and BER is less than 10-5 at 10dB SNR for self cancellation scheme whereas BER is 10-1 at 0dB SNR and greater than 10-5 at 10dB SNR for the proposed improved cancellation scheme. But for the frequency offset 0.2, by using the self-cancellation method BER greater than 10-1 at SNR = 0dB and BER less than10-4 at SNR = 10dB and for proposed method BER is 10-1 for 0dB SNR and BER is just less than 10-5at 10dB SNR. So proposed improved cancellation scheme is better than ICI self-cancellation in [21]. Fig. 2 shows the comparison of the BER for higher alphabet size (16-QAM OFDM system) at N = 64. Fig. 3 shows the comparison of proposed technique with self cancellation scheme in terms of the carrier to interference ratio (CIR). Fig. 4 shows the comparison of proposed scheme with self cancellation scheme with reference to ICI coefficient before and after cancellation of ICI. The proposed result is comparable with [22].
0 1 2 3 4 5 6 7 8 9 10
Eb/No in dB
Fig. 1: BER Comparison between proposed improved ICI cancellation schemes with self cancellation scheme for BPSK OFDM system
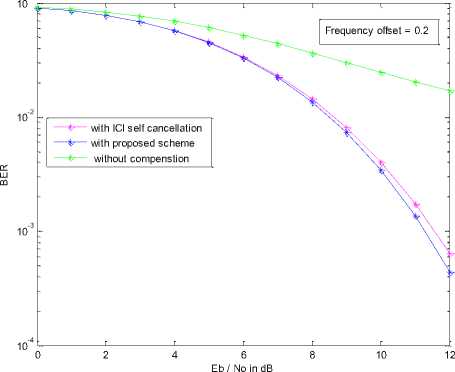
Fig. 2: BER Comparison between proposed ICI cancellation schemes with self cancellation scheme for 16-QAM OFDM system
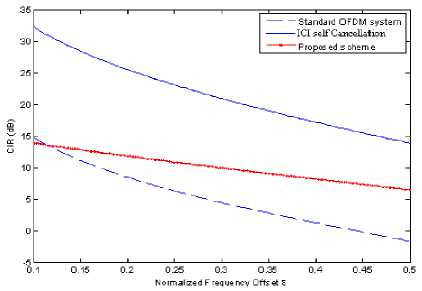
Fig. 3: Comparison of proposed scheme with self cancellation scheme in terms of CIR
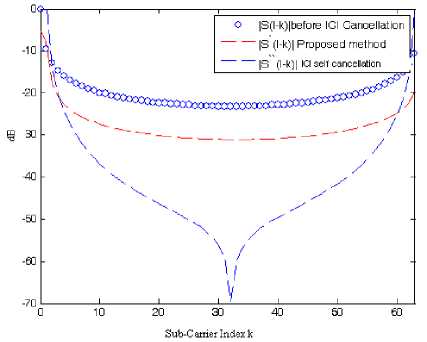
Fig. 4: Comparison of ICI coefficient of proposed scheme with self cancellation scheme
-
V. Conclusion
In this paper, a simple improved ICI cancellation technique has been explored to reduce the frequency offset sensitivity of OFDM digital communication systems. The proposed technique use parallel ICI cancellation technique for mitigation of ICI in OFDM communication systems. From the simulation results it is clear that the proposed technique is better than self cancelation scheme. The theoretical analysis and simulation results prove that ICI caused by frequency offset can be cancelled by using the proposed technique for the OFDM digital communication systems.
Acknowledgements
The author is very much thankful to the potential reviewers for their critical comments and suggestions to improve the quality of the manuscript.
Список литературы BER Analysis of OFDM Digital Communication Systems with Improved ICI Cancellation Technique
- R. Prasad, “OFDM for Wireless Communications,” Artech House, Boston, 2004.
- A. R. S. Bahai, B. R. Saltzberg, and M. Ergen,“Multi-Carrier Digital Communications – Theory and Applications of OFDM,” 2nd ed., Springer-Verlag, New York, 2004.
- T. Hwang, C. Yang, G. Wu, S. Li, and G. Ye Li, “OFDM and its wireless applications: a survey,” IEEE Trans. on Veh. Tech, vol. 58, no. 4, May 2009, pp. 1673-1694.
- T. Pollet, M. V. Bladel, and M. Moeneclaey, “BER sensitivity of OFDM systems to carrier frequency offset and Wiener phases noise,” IEEE Trans. Commun., vol. 43, no.234, 1995, pp. 191–193.
- R. Li and G. Stette, “Time-limited orthogonal multicarrier modulation schemes,” IEEE Trans. Commun., vol. 43, no. 234, 1995, pp. 1269–1272.
- Y. Zhao and S.-G.Haggman, “Inter-carrier interference self-cancellation scheme for OFDM mobile communication systems,” IEEE Trans. Commun., vol. 49, 2001, pp. 1185-1191.
- Y.Zhao, J.-D.Leclercq, and S.-G.Haggman, “Inter-carrier interference compression in OFDM communication systems by using correlative coding,” IEEE Commun. Lett., vol. 2, 1998, pp. 214–216.
- P. H. Moose, "A technique for orthogonal frequency division multiplexing frequency offset correction," IEEE Trans. Commun., vol.42, no.10, Oct. 1994, pp. 2908-2914.
- J. Armstrong, “Analysis of new and existing methods of reducing intercarrier interference due to carrier frequency offset in OFDM”, IEEE Trans. Commun., vol. 47, no. 3, Mar. 1999, pp. 365-369.
- C. Muschallik, "Improving an OFDM reception using an adaptive Nyquist windowing," IEEE Trans. Consumer Electron., vol. 42, no. 8, Aug. 1996, pp. 259-269.
- H.-G. Yeh and Y.-K.Chang, “A conjugate operation for mitigating intercarrier interference of OFDM systems,” Proc. Vehicular Technology Conference, 2004, Atlanta, vol. 6, Sept. 2004, pp. 3965-3969.
- Wei Bai and Y. Kim, “Effects of correlative coding on OFDM systems for intercarrier interference suppression,” IEEE Trans. Vehicular Technology, vol. 56, no. 6, 2007, pp. 3732-3738.
- Y.Zhang and H. Liu, “Frequency-domain correlative coding for MIMO-OFDM systems over fast fading channels,” IEEE Commun. Lett., vol. 10, 2006, pp. 347–349.
- Y. Zhang and H. Liu, “Decision-feedback receiver for quasi-orthogonal space-time coded OFDM using correlative coding over fast fading channels,” IEEE Trans. on Wireless Commun., vol. 5, no. 11, Nov. 2006, pp. 3017–3022.
- N. C. Beaulieu and P. Tan, “On the use of correlative coding for OFDM,” Proc. of IEEE Int. Conf. on Communication (ICC 2007), June 24–28, 2007, pp. 756–761.
- K.Sathananathan and C.Tellambura, “Forward error correction codes to reduce inter-carrier interference in OFDM,” Proc. of IEEE Int. Symp. on Circuits and Systems (ISCAS 2001), vol. 4, May 2001, pp. 566-569.
- M. J. Fernandez-Getino Garcia, O. Edfors and J. M. Paez-Borrallo, “Frequency offset correction for coherent OFDM in wireless systems”, IEEE Trans. Cons. Elect., vol. 47, no. 1, Feb. 2001, pp. 187-193.
- Sanjiv Kumar, P. K. Gupta, G. Singh and D. S. Chauhan, “Performance analysis of Rayleigh and Rician fading channel models using Matlab simulation” IJISA, vol. 5, no. 09, 2013, pp. 94-102.
- J. Ahn and H. S. Lee, “Frequency domain equalization of OFDM signal over frequency nonselective Rayleigh fading channels,” Electron. Lett., vol. 29, no.16, 1993, pp. 1476–1477.
- K. Sathananantan and R. M. A. P. Rajatheva, “Analysis of OFDM in presence of frequency offset and method to reduce performance degradation”, Proc. IEEE Globcom., 2000, San Fransisco, CA, Nov. 2000, vol. 1, pp.72-76.
- Yu Fu and C. C. Ko, “Theoretical BER analysis of OFDM system with ICI self cancellation”, Proc. 5th Int. Symposium on Wireless Personal Multimedia Communication, Honolulu, HI, USA, Oct. 2002,vol. 3, ,pp. 991-994.
- Y.-H. Peng, Y.-C. Kuo, G.-R. Lee, and J.-H. Wen, “Performance analysis of a new ICI-self-cancellation-scheme in OFDM systems”, IEEE Trans. Consumer Electronics, vol. 53, no. 4, Nov. 2007, pp. 1333-1338.


