Бесконечно малые MG-деформации овалоида

В этой работе изучается поведение овалоида положительной гауссовой кривизны относительно бесконечно малых деформаций, при которых сохраняется поточечно грассманов образ поверхности, а вариация гауссовой кривизны задается как функция σ на поверхности. Сохранение грассманова образа — известное условие G-деформаций [1]. Задание вариации гауссовой кривизны как известной функции на поверхности напоминает нам о проблеме Минковского [2]. Поэтому такие деформации будем называть бесконечно малыми MG-деформациями.

Будем считать, что овалоид и векторное поле MG-деформации ~y принадлежат классу D 3 ,p , P> 2. 1                                                            ^

Если векторное поле MG-деформации имеет только вид ~y = const, то будем говорить, что овалоид является жестким относительно бесконечно малых MG-деформаций.

В § 1 выводится уравнение бесконечно малой MG-деформации для поверхностей гауссовой кривизны K > k 0 > 0, k 0 = const, в трехмерном евклидовом пространстве. В § 2 проводится исследование решений уравнения бесконечно малых MG-деформаций для овалоида. Основной результат работы сформулирован в виде теоремы, которая доказывается в § 3.

Теорема. Для каждой функции σ существует единственная бесконечно малая MG -деформация овалоида положительной гауссовой кривизны, векторное поле деформаций которой определяется с точностью до постоянного вектора. Овалоид является жестким относительно бесконечно малых MG -деформаций тогда и только тогда, когда вариация гауссовой кривизны тождественно равна нулю (σ ≡ 0) .

¹ Используются обозначения книги [3].

§ 1. Бесконечно малые MG-деформации

Рассмотрим поверхность S : ~ = ~(u 1 , u ² ), (u ¹ , u ² ) E D, D — область.

Определение 1. Непрерывной по параметру t деформацией S _t поверхности S называется непрерывное отображение любого промежутка, содержащего нуль, например [0,1], в банахово пространство C n (D) вектор-функций такое, что S o = S, а S t для любого 1 из рассматриваемого промежутка есть регулярная поверхность класса C n (D).

Определение 2. Если вектор-функция ~ _t (u ¹ , u ² ), задающая поверхность S t , обладает частными производными порядка k :

∂ ^l ~r t

"д^Т, l = 1,2, ■ ■", k, каждая из которых есть непрерывное отображение рассматриваемого числового промежутка в Cn(D), то непрерывная деформация St называется деформацией класса Ck по параметру.

Определение 3. Функция

S^u^u ² ) =    dr t      , l = 1, 2,..., k,

2l! dr t =0

называется l-й вариацией (по Рембсу ) радиус-вектора ~ = ~(u 1 , u ² ) поверхности S при деформации S _t .

Определение 4. Пусть S _t — деформация поверхности S класса C ^k по параметру, k = 1, 2,..., го . S t называется бесконечно малой MG-деформацией поверхности S, если

6K = ст, 6~ = 0,

где ст — заданная функция на поверхности S , ст E D i ,p , p >  2.

Разложим радиус-вектор поверхности S t по степеням t: ~ _t = ~ + 2(t5~ + t ² 5²~ + ...), t E [0,1], где ~ = ~(u 1 , u ² ) — радиус-вектор исходной поверхности. Обозначим 5~ = у — векторное поле деформации.

Наша задача: найти векторное поле у = ~(u 1 , u ² ). Для этого нам понадобится преобразовать условия (1), таким образом, мы получим уравнение бесконечно малых MG-деформаций.

Будем рассматривать односвязные поверхности гауссовой кривизны K >  k о > 0, k o = const.

Рассмотрим условие 6~ = 0:

V [8 1 ~,8 2 ~ ]\     5[д 1 ~,д 2 ~ ] •| [8 1 ~, 8 2 ~] | - [8 1 ~,8 2 ~ ] • О( | [8 1 ~,8 2 ~ ] | )

ОП = О ,_г„ ^ „      = -------------------------------5-------------------- = 0,

V | [д 1 ~, д 2 г ]|/                               | [8 1 ~,8 ₂ ~] |²

где 8 j ~ = дд~ . Это условие выполняется тогда и только тогда, когда числитель равен нулю

5[д ₁ Г, д ₂ r ] • | [д ₁ Г, д ₂ r ] | — [d ₁ r, д ₂ г ] • 5( | [d ₁ r, д ₂ г ] | ) = 0.                       (2)

К тому же

О( | [d 1 r, 8 2 т ] | ) = 5 p [d 1 r, d 2 r ] ² = 2 ([d 1 r, 8 2 т ] ² ) ² • 5([d 1 r, 8 2 т ] ² )

2p[8 1 т, 8 2 т ] ²

• 2[8 1 т, 8 2 т ] • ([5(8 г r ),8 2 т ] + [8 1 т,5(8 ₂ т )])

| [8 1 т, 8 2 т ] |

([81т, 82т ], [81у, 82т ] + [81т, 82У]), и уравнение (2) принимает вид

([d i y , d 2 ~] + [d i ~, d 2 ~]) • | [d i ~, d 2 ~] | ² - [d i ~, d 2 ~] • ([d i ~, d 2 ~], [d i ~, d 2 ~] + [d i ~, d 2 ~]) _ 0

| [d i ~, d 2 ~ ] |                                                                ‘

Это равенство справедливо тогда и только тогда, когда

([d i ~, d 2 ~] + [d i ~, d 2 ~]) • P i - [d i ~, d 2 ~] • P 2 _ 0,

где P _i _ | [d _i ~, d ₂ ~] | ² и P 2 _ ([d _i ~, d ₂ ~], [d _i y,d ₂ ~ ] + [d _i ~, d ₂ ~]) — скалярные величины. Умножая равенство (3) скалярно на d i ~, а затем на д 2 ~, находим (d i ~, d 2 ~, d i ~) _ 0 и (d i r, д 2 у, д 2 r) _ 0. Это означает, что векторы d i r, д 2 r, d i y, д 2 у компланарны.

Следовательно, ∂ 1 y, ∂ 2 y можно разложить по векторам ∂ 1 r, ∂ 2 r :

9$ _ a j d _k r, j _1,2,                             (4)

где aj — некоторые скалярные функции от ( u ¹ , u ² ).

Продифференцируем первое равенство системы (4) по u ² , а второе по u ¹

{ d i2 y _ d 2 a i d i r + a l d i2 r + d 2 a 1 d 2 r + a 1 d 22 r, d 2i y _ d i a 2 d i r + a 2 d_nr + d i a^r + a 2 d 2i r.

Используем деривационные формулы Гаусса d jk r _ r jk d i r + b jk n, j, к ⁼ 1, 2,

Jdi2y _ d2aidir + ai(r12dir + r12d2r + bi2n + d2a1d2r + a1(r22dir + Г22d2r + b22n), (d2iy _ dia2dir + a2(ri1 dir + r11d2r + bnn) + dia^r + a2(r21 dir + Г21 d2r + b2in), где bjk, j,k _ 1, 2, — коэффициенты второй квадратичной формы исходной поверхности. Так как di2y _ d2iy, то, приравняв коэффициенты при dir, d2r и n, получим систему d2ai + airi2 + air22 _ dia2 + a2rii + a2r21,

< д 2 a ² + a i Г 22 + a ² Г 22 _ dia 2 + a 2 r 21 + a^ i ,                   (5)

^a^bi2 + a ² b 22 _ a 2 b ii + a^ i .

Так как гауссова кривизна исходной поверхности S : K >  к о > 0, к о _ const, то, вводя на S сопряженно изометрическую систему координат, в которой b 11 _ b 22 _ 0, b i2 _ 0, получим a ² _ a 2 . Система (5) преобразуется в систему

Г ^d 2 ^a i - ^di^a 2 ^{_ ( a} 2 - ^a i ^)r 2i ^{+ a} 2 ^(r ii - г 22 ), (d₂a 2 — dia 2 _ (a 2 — a 1 )Г 2₂ + a 2 (Г 2₁ — Г 2₂ ).

Теперь, следуя В. Т. Фоменко [2, с. 87], введем обозначения: U _ 2 (a 2 — a i ), V _ a ² , П _ 2 (a 2 + a i ). Тогда a i _ П — U , a 2 _ П + U . Уравнения (6) принимают вид

(diU — d 2 V + 2Г 22 и + (r 2 1 — r 22 )v _ — d i n, (d 2 и + diV + 2Г 2 1 и + (r i 1 — r 22 )v _ d 2 n.

Таким образом, условие 6n _ 0 привело нас к системе (7).

Рассмотрим условие 5K = ст.

Пусть g = giig22 — g^, b = biib22 — b2_2 — дискриминанты первой и второй квадратичных форм исходной поверхности соответственно. Тогда K = g и b           δb · g - b · δg

51g I = ст, -------g2------- = ст, отсюда следует равенство

5b — K • 5g = дст.

Проварьируем g и b :

⁵ g = ⁵ g ii • g 22 + g ii • ⁵ g 22 - 2g i2 • °g i2 ,

5b = 5b ii • b 22 + b ii • 5b 22 — 2b i2 • 5b i2 .

Вычислим вариации 5g jk и 5b jk , j, k = 1, 2, выражая их через a i , a ² , a 2 , учитывая, что 5~ = ~, 5~ = 0, имеем

5g _ii = 5(di~, di~) = (5(di~ ),di~) + (di~, 5(di~)) = 2(di~, di~) = 2(a^di~ + a 2 d 2 ~, di ~) = 2a^g_n + 2a 2 g 2i ,

5g i2 = 5(di~, d 2 ~) = (5(di~), d 2 ~) + (di~, 5(d 2 ~)) = (di~, d 2 ~) + (d 2 ~, di~) = (aidi~ + a 2 d 2 ~, d 2~) + (a ² di~ + a 2 d 2 ~, di~) = a^g i2 + a 2 g 22 + a 2 g ii + a^ i ,

5g 22 = 5(d 2 ~, d 2 ~) = (5(d 2 ~), d 2 ~) + (d 2 ~, 5(d 2 ~)) = 2(d 2 ~, d 2 ~)

= 2(a 2 di~ + a 2 d 2 ~, d 2 ~) = 2a 2 g i2 + 2a 2 g 22 .

Продифференцируем первое из уравнений (4) по u ¹ , а второе — по u ² :

di i~ = dia^di~ + aidi i~ + dia2 d2~ + a2 d2i~, d22~ = d2a2di~ + a2di2~ + d2a2 d2~ + a2 d22~.

Используя эти равенства, а также формулу d i2 ~ = d 2 a^di~ + a^d i2 ~ + d 2 a 2 d 2 ~ + a 2 d 22 ~, находим

5b ii = (5(di i r ),n) + (di i r,5n) = (di i y, n) = a i (di i r, n) + a 2 (d 2i r, n) = a^bn + a 2 b i2 ,

5b 22 = (5(d 22 r ),n) + (d 22 r, 5n) = (d 22 y, n) = a 2 (d i2 r, n) + a 2 (d 22 r, n) = a 2 b i2 + a 2 b 22 ,

5b i2 = (5(d i2 r ),n) + (d i2 r, 5n) = (d i2 y, n) = a i (d i2 Г, n) + a 2 (d 22 r, n) = a^b i2 + a 2 b 22 .

Учитывая, что b ₁₁ = b ₂₂ = 0, b _i2 = 0, получаем 5b ₁₁ = a^b ti , 5b ₂₂ = a2^ i , 5^ 2 = a ² b ₁1 .

Подставляя найденные вариации в (9), получаем

5g = 2g 22 (a^g_n + a 2 g 2i) + 2gi i (a 2 g i2 + a 2 g 22) — 2g i2 (a^g i2 + a 2 g 22 + a 2 g ii + a 2 g 2i) ,

5b = a b 11 • b 22 + b 11 • a ² ₂ b 11 — 2 b 12 • a ² b 11 = b 1 b 1 a ¹ ₁ + a ² ₂ .

Подставляя эти выражения в (8), находим biibii (ai + a2) — 2Kg22 (a^gn + a2g2i) — 2Kgii (a2gi2 + a2g22) + 2Kgi2 (a^gi2 + a2g22 + a2gn + a2g2i) = gCT.

Перегруппировав это выражение, приводим его к виду

(a i + a 2 )(b_n b ii - 2Kg) = ga,

отсюда имеем

( ^a 1 + ^a 2 ) = - ^.

Сделаем замену П = 2 (a 2 + a i ). Тогда уравнение (10) принимает вид

П =

σ

2к‘

Таким образом, система (1) привела нас к системе

' diU - d 2 V + 2г 22 и + (г 2 1 - г 22 ) v = -d i п ,

* d 2 U + diV + 2г 21 и + (г 11 - г 22 ) v = д 2 П,                    (12)

.П =

σ

2 K^.

Благодаря третьему уравнению системы (12) функция П у нас фактически известна, так как K и a известные и заранее заданные функции, поэтому вместо функции П мы подставим в первые два уравнения системы (12) ее значение - ₂ ^σ _K . Получается система двух уравнений с двумя неизвестными U и V

Г д^и - d 2 V + 2^ и + (r 2i - ^)v = d i (^к) , [^д 2 U ^{+ d}lV ^{+ 2r} 2i U ^{+ (r} ii ^{- r} 22 ^{) V} = ^{- д} 2 ( 2 K )•

Теперь, следуя И. Н. Векуа [3, с. 111], вводим в рассмотрение функцию w(z) = U + iV , где z = u ¹ + iu ² , (u¹,u ² ) G D, и записываем полученную систему в виде одного уравнения:

d z w + Aiw + Biw

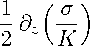
где

A i = 4 (^r ii ^{- Г} 22 ^{+ 2Г} 22 ) ^- 4 (^Г 21 ^{- Г} 22 ^{- 2Г} 21 ),

Bi = 4 (r22 - rl i + 2Г22) + 4 (r2i - r22 + 2ri2), dz w =2 (diw + id2w),

∂ z

σ

K

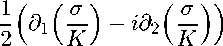
Преобразуем уравнение (13).

Сог ласн о d ^d _i in qg v K.

ставляем w в

[3, с. 100] коэффициент A 1 может быть представлен в

Введем в рассмотрение функцию ги = w

(13) и, учитывая, что A i = dh in

d z w + B _i ги =

g ^√ K

виде A i =

g ^√ K . Тогда

w=

w √ _g √ _K

Под-

, приводим уравнение (13) к виду

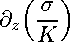
Решив уравнение (14), мы найдем функцию ги а значит, найдем U = Re { w(z) } , V = Im { w(z) } .

w g ^√ K,

отсюда вычислим w,

Зная U и V, с помощью формул а ^ = П — U , а ^ = П + U , а ² = V и (11) получим а 1 , 2    2

^а 1 , ^а 2 *

Система (4) является пфаффовой системой, причем условие интегрируемости пфаффовой системы выполняется тождественно, поэтому соотношение dy = d i ~du ¹ + d 2 ydu ² , является полным дифференциалом. Интегрируя его, находим вектор смещения MG-деформации ~y с точностью до постоянного вектора в силу односвязности поверхности.

Таким образом, задача нахождения вектора смещений бесконечно малых MG-деформаций эквивалентна решению уравнения (14), поэтому уравнение (14) будем называть комплексным уравнением бесконечно малых MG-деформаций поверхностей положительной гауссовой кривизны.

§ 2. Исследование решений уравнения бесконечно малых MG-деформаций овалоида

Общее решение неоднородного уравнения вида (14), следуя И. Н. Векуа [3, с. 130], будем искать в виде w = wo + w*,                                 (15)

т. е. общее решение неоднородного уравнения вида (14) равно сумме общего решения однородного уравнения и какого-либо частного решения неоднородного уравнения.

Для того чтобы отыскать общее решение однородного уравнения dzwo + Biwo = 0,                               (16)

исследуем поведение функции w o на бесконечности.

Пусть S — овалоид положительной гауссовой кривизны. Выберем на овалоиде две диаметрально противоположные точки P i , P ₂ , которые будем называть полюсами. С помощью стереографической проекции из полюса P i взаимно однозначно отобразим ова-лоид на плоскость (u ¹ , u ² ), при этом полюс P 2 отобразится в точку z = u ¹ + iu ² = 0, а полюс P 1 в точку z = u ¹ + iu ² = го .

Теперь с помощью стереографической проекции из полюса Р ₂ взаимно однозначно отобразим овалоид на плоскость (^,п), при этом полюс P 1 отобразится в точку Z = Z + in = 0, а полюс P 2 в точку Z = ^ + in = го .

Таким образом, мы получили две карты (u 1 ,u ² ) и (£,n)- Переход от одной карты на другую происходит при помощи конформного преобразования вида Z = Z •

Исследуем поведение решения однородного уравнения в окрестности точки z = го .

Для любого скалярного или векторного инварианта на овалоиде (обозначим его через s) справедливо следующее соотношение:

_ ds dZ + ds dZ

Так как Z = Z , Z = z , то Z z = d! = - - 2 , H = 0, к 1 ^ 0, s z = ds • ( - z 2 )=O( ^{| z} | ^{- 2} ) при | z | ^ ^ro .

_∂ ^∂ _ζ ^s ограничено, так как при | z | → ∞ ,

ds dZ ds dZ s ^z    dZ dz d( dz ‘

Так как Z = 'Z , Z" = Z , то ^d z = 0, (^ 5 = ^dZ = — z 2 . Следовательно (учитывая, что s z ограничено), s _g = || • ( — ^ = O (|z | ^{- 2}) при | z | ^ ro .

Изучим поведение dj ~, j = 1, 2, dz~ = 2 (di~ + id2~), dz~ = 2 (di~ - id2~).

Складывая эти два равенства, находим d i ~ = d _z ~ + d _z ~. Отсюда следует, что d i ~ O( | z | ^{- 2} ) при | z | ^ го . Вычитая из первого равенства второе получим id 2 r = d _z r — d _z Отсюда следует, что д 2 Г = O( | z | ^{- 2} ) при | z | ^ го .

II TsJ

Аналогично доказывается, что d j n = O( | z | ^{- 2} ), d j y = O( | z | ^{- 2} ), j = 1, 2.

Итак, частные производные радиус-вектора овалоида ведут себя как O( | z | ^{- 2} ), поэтому коэффициенты первой квадратичной формы овалоида ведут себя как O( | z | ^{- 4} ):

g j = (d i r,d j r) = O( | z |   ² )O( | z |   ² ) = O( | z |   ⁴ ),    i,j = 1, 2, | z | ^ го .

Тоже справедливо и для коэффициентов второй квадратичной формы овалоида: b ij = —(d i r,d j n) = O( | z | ^{- 2} )O( | z | ^{- 2} ) = O( | z | ^{- 4} ), i,j = 1, 2, | z | ^ го .

Следовательно, g = giig22 — g?2 = O(|z|-4 )O(|z|-4) — (O(|z|-4 ))2 = O(|z|-8), b = bnb22 — b22 = O(IzI-4)O(IzI-4) — (O(IzI-4))2 = O(IzI-8), |zI ^ го,

K =b=°( 5^ = ^{о (1)}’       го

Исследуем поведение на бесконечности функций a i , a i , a 2 . Воспользуемся соотношениями 5Ьц = a i b ii + a i b i2 , Sb i2 = a i b i2 + a i b 22 • Так как

^b ii = — (diy,d₁n) = O( | z | ^{- 2} )O( | z | ^{- 2} ) = O( | z | ^{- 4} ),

Sb12 = —(diy,d2n) = O(|z|-2 )O(|z|-2) = O(|z|-4), bi i = b22 = 0, bi 2 = 0, то по правилу Крамера получаем

ai —	Sb ii Sb i2	b i2 b 22	b 22 Sb ii	O( | z | - 4 )O( | z |	- 4 — = O(1),
		b	= b	O( | z | - 8 )
	b ii	Sb ii
a i =	b i2	Sb i2	_ bii 5b i2	_ O( | z | - 4 )O( | z |	- 4 — = O(1).
		b	b	O( | z | - 8 )

Аналогично из соотношений Sb ₂₂ = a 2 b _i2 + a 2 b ₂₂ , Sb _2i = a 2 b _ii + a 2 b _2i получаем, что a ² ₂ = O(1).

Из этого следует, что U = 2 (a 2 — a i ) = O(1), V = a i = O(1), следовательно, w =

U + iV = O(1). Тогда w = waJ gVK = O(1)O( | z | ^{- 4} )O(1) = O( | z | ^{- 4} ), | z | ^ го .

Исследуем ге * на бесконечности. Частное решение неоднородного уравнения вычисляется по формуле [3, с. 154]

w * =

— 1 JJ ^ i (z,Z,D)F (Z) d^dn — 1Ц ^ 2 (z,Z,D)F(Z) d^dn,

D

D

где Q1(z,Z) =    ", ^(z.Z) — w∗

-

i e Vp₊ + .-'                              e ^ i _— e ^ 2

2П // [ 2(< - z) ^{( Re {} F ^{} +} i ^{Im {} F ^{} ) +} 2(< - z)

D

( Re { F }- i Im { F }) d^dn

- - ПП D

еш1 Re{F} + ie^2 Im{F} ζ-z dξ dη.

Обозначив f (Z) — е ^ш 1 Re { F } + ie ^ ² Im { F } , получаем w * — — П JJ D f—z d^ dn — T D f . Докажем, что f E L p, 2 , p >  2. Из [3, с. 139] известно, что | w j | 6 M p , следовательно, | e ^ ^j | 6 e ^M p , j — 1, 2. Отсюда следует е ^ш з — 0(1).

g ^√ K

F — ----- 2

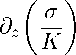
g ^√ K

∂ z σ · K - σ · ∂ z K

K ²

0( | z | - ‘ )O( | z | ^{- 2} )— O( | z | ^{- 6} ).

Следовательно, f (Z) E L p, 6 , p >  2, поэтому можем считать, что f E L _p, 2 , p >  2.

Таким образом, f удовлетворяет условию теоремы 1.24 из [3, c. 44], из которой 2-p следует, что вблизи бесконечности TDf убывает как |z| "Г", p > 2, т. е. w* — TDf — O(|z| p ), p > 2, |z| ^ го. Наконец, из формулы (15) следует, что wo — w*

— w — o( | z | ^pP ) — O( | z | ⁴ ) — o( | z | p ),

p >  2, | z | ^ го .

Из [3] известно, что B i E L _p , 2 (D), p >  2, D — вся комплексная плоскость, но в явном виде это утверждение в [3] не доказывается, поэтому сформулируем его в виде леммы и приведем подробное доказательство.

Лемма. Коэффициент B i E L _p , 2 (D) , p >  2 , D — вся комплексная плоскость.

C Коэффициент B i — — B [3, c. 323]. Из [3, c. 99] известно, что

— ^{— 4}(r zz . r ^{z ) + 4}(r z r cz),,  — ^{— 8}(r z . r zz ),

^^ — 8(r z ,r zz ).

∂z

Так как D — вся комплексная плоскость, то ее конформные преобразования исчер-

пываются формулой Z — фz + _p , причем ец

— фХ — 0.

Положим е — 0, Х — 1, ф — 1, ц — 0.

При конформном преобразовании Z — z ^:

r z — ~ z • Z z ,    r z — ~ Z • Z e ,   r z E — (~ z • Z e ) x — ~ Z C • Ze + ~ Z "  Z e e -

Аналогично tee — rzE " Z"e " Zz, а+ — 4(rz .~e )— 4(rz Zz ,rZ Zz) — 4(rZ .4 )Zz Zz— а+Zz Zz.

а - — 4(r z ,~ e ) — 4(~ Z z ,~ Z e ) — 4(~,~ )Z E — а^^ ² , а — |(а ⁺² — | а - | ² ) — | (а +2 Z z ^{2 Z} E — | а _ Z Z | ² ) — | (а +2 — | а _ | ² ) l Z E | ⁴ — a * |Z E | ⁴ .

"di" = ⁴⁽~ zz , r Z ) + 4(~ z ,r Zz ) = 4(~ zz^Zz G, ~ zG ) ^{+ 4(}~ z C z ,~ zz • < 2 ⁺ r z • Gz )

7 2               7 2              7 ^d a ⁺   7 2    + 7

= ⁴⁽r( Z ’rC ^{) Z} Z ^Z Z ^{+ 4(}rC,r( Z ^{) Z}Z ^Z Z ⁺⁴⁽rC,r( ^{) Z} Z ^Z z Z = ^7 ^Z z ^Z z ⁺ a * ^Z z Gz ,

∂a

-d— = 8⁽r z , r z z ) = 8^{( r}z^Zz , r z z • ^Z Z ^{+ r}z • ^Zz z ) = 8^{( r} Z , ^rZZ ^{) Z} f ^{+ 8(}r ^z , r z ) • GGz

∂a_{∗        -}

= “^Zz + 2a* • ZZZzZ, ∂ζ z ∗ da —  ^-7      7zX             72 z _ da* 72z

-д^- = ⁸⁽r z ^zz , r zz • GG) = ⁸⁽r<,r z z ⁾ • ^Z z ^{Z z} = "dz"" • ^Z z ^{Z z} ‘

Тогда

1 / - da ⁺ ₊ да _ da — I 2a _ — a — a —— 8a \ dz dz dz

8a * | Z z | ⁴

+

— 7 2I ^da * z 7 2 ,   + Z 7    1

I ^{2 a} * ^Z z I zj7 G ^Z z ⁺ a * ^Z z ^Z zz ) ∗ z _∂ζ z ∗

₇ da _{7       - 7 7}

^— a * ^Z z ^Z z I _ят ^Z z ^{+ 2a}* GGz )

∗         _∂ζ z ∗

-

- 7 2 ^da * . 72z a * ^Zz dz ^Z z ^Z;

z

_R ^Z z ^Z z

* I Z z | ⁴ ’

Г' ПА R - - 1 (9л — da- _ Л + da- _ Л — da*^

где B*     8a* ^a* dz    a* dz    a* dz.'

Так как при |z| ^ го имеем Z ^ 0, то B* = O(1), тД4 = O/H-s) = O(1), Zz = — 1^ = |zz|          O/|z| )

O( | z | ^{— 2} ), это означает, что B = O( | z | ^{— 2} ) при | z | ^ го , следовательно, B i = O( | z | ^{— 2} ) при | z | ^ го , и B 1 G L p, ₂ (D), p >  2. B

Итак, функция ге д ограничена и является решением однородного уравнения (16), где B i G L _p, 2 (D), p >  2 (в силу леммы). Так как ге д = O ^|z |""p"" ^, p> 2 при | z | ^ го , то ге д обращается в нуль в точке z = го .

Таким образом, ге д является обобщенной аналитической функцией, удовлетворяющей условию обобщенной теоремы Лиувилля [3, c. 128].

Из этой теоремы следует, что te g (z) = 0 всюду на плоскости D.

§ 3. Доказательство теоремы

Итак, мы показали, что te g (z) = 0 всюду на плоскости D. Тогда соотношение (15) имеет вид ге = ге * . Получается, что каждому ст соответствует единственное решение ге.

Функция г = ,w = >w* —, U = Re{г}, V = Im{г}, следовательно, а2 = Im{г}, gK gK а1 = П — U = — 2K — Не{г}, а2 = П + U = — 2K + Не{г}. Уравнения (4) принимают вид:

( d ₂ y = ( — 2 K — Re { w } )d ₁ r' + Im { w } d ₂ r', ( d 2 ~ = Im { w } d₁r' + ( — 2 K + Re { w } )d 2 r.

Так как рассматриваемая поверхность односвязна, то с помощью уравнений (17) можно найти поле смещений бесконечно малой MG-деформации, соответствующей конкретному ст, с точностью до постоянного вектора, интегрируя выражение dy = d i y du¹ + d 2 y du ² .

Таким образом, для каждого σ существует единственное поле бесконечно малой MG-деформации с точностью до постоянного вектора.

Докажем теперь, что овалоид является жестким относительно бесконечно малых MG-деформаций тогда и только тогда, когда ст = 0.

Пусть ст = 0. Тогда F = g ^ KK d z ( — ) = 0. Следовательно,

w * =

П Ц ^ i (z,Z,D)F (Z) ■■• - П Ц ^ 2 (z,Z,D)F(Z) ■■• = 0.

D

D

Тогда w =

w ∗

gK

= 0, и соотношения (17) принимают вид:

( d i ~ =0, I d 2 ~ =0.

Отсюда следует жесткость овалоида.

Пусть овалоид является жестким относительно бесконечно малых MG-деформаций, т. е. y = C = const. Тогда dy = d 1 ydu 1 + d ₂ ~du 2 = 0. Следовательно, справедливы равенства (18). Тогда в силу соотношений (17) имеем

( ( — 2 — — Re { w } )d 1 ~ + Im { w } d ₂ ~ = 0, [ Im { w } d 1 ~ + ( — 2 — + Re { w } )d 2 ~ = 0.

Умножая скалярно первое из этих равенств на — d i n, а второе — на — д 2 П, учитывая, что b 11 = b ₂₂ = 0, b ₁₂ = 0, получаем

( ^— 2 — ^{— Re { w }} = 0, |^^— 2 — + Re { w } = 0.

Отсюда следует, что ст = 0.