Бесконтактный метод формования элементов транспортных сооружений из органоминеральных композиционных материалов

Носов О.А., Варданян Г.Р., 2014

В последнее время наблюдается интенсивный рост объемов применения органоминеральных композиционных материалов в различных отраслях народного хозяйства страны, таких как машиностроение, приборостроение, авиа- и ракетостроение, строительство, жилищно-коммунальное хозяйство и другое. Востребованность в таких материалах вызвана тем, что различные элементы существующих конструкций подвергаются внешним воздействиям, которые можно разделить на несколько групп: механические, физико-химические, температурные и комплексные воздействия, представляющие собой сочетание указанных видов. Под влиянием данных факторов в деталях машин, транспортных сооружениях, строительных конструкциях и др. возникают повреждения, которые значительно снижают срок эксплуатации и экономическую эффективность.

Органоминеральные композиционные материалы - многокомпонентные материалы, состоящие из пластичной основы (матрицы), армированной наполнителями. В качестве компонентов могут использоваться самые разнообразные материалы - бумага, керамика, стекла, пищевые отходы, углерод и др. Наполнитель определяет механические свойства материала (прочность, жесткость, износостойкость и другие свойства), а матрица обеспечивает монолитность материала, передачу напряжения в наполнителе и стойкость к различным внешним воздействиям. Варьируя состав и соотношение материалов матрицы и наполнителя, получают широкий спектр новых материалов с требуемым набором свойств [1].

Существуют следующие основные виды органоминеральных композиционных материалов:

• -    композиционные материалы, содержащие любые твердые частицы или волокна;

• -    смеси композиционных материалов;

• -    композиционные материалы, содержащие жидкости в виде включений или пластификаторов;

• -    композиционные материалы, содержащие газообразные наполнители.

Одним из наиболее простых и сравнительно недорогих процессов получения органоминеральных композиционных материалов является литьё в формы. Этим методом могут быть получены листы, трубы, стержни и другие изделия требуемой формы. [2]

Применяемые в качестве матрицы материалы должны обладать высокой адгезионной способностью, которая является одним из факторов, определяющих прочность органоминерального композиционного материала.

Следует отметить, что адгезия в процессе отливки заготовок элементов конструкций играет негативную роль, то есть материал прочно связывается с рабочими поверхностями оборудования. Для устранения прилипания к поверхностям оборудования и повышения рентабельности производства применяют твердые антиадгезионные покрытия или жидкие смазки. Следует отметить, что первые дорогостоящи и недостаточно долговечны, а вторые существенно изменяют поверхностные свойства изделий, что затрудняет последующую обработку, например, процессы окрашивания или нанесения люминесцентных покрытий.

Создание воздушного буферного слоя между контактирующими поверхностями оборудования и изделия на сегодняшний день является единственным способом устранения контакта. Воздушный буферный слой образуется за счет истечения сжатого воздуха через перфорацию рабочей поверхности оборудования, полностью разделяя ее с опорной поверхностью изделия. При этом можно не только исключить адгезию, но и обеспечить оптимальный режим обработки, не нарушая поверхностных свойств изделия (в частности охлаждение полученного изделия) [3, 4].

Следует отметить, что формование литьем на воздушный буфер, сопровождаемый первоначальной загрузкой и дальнейшими сложными гидрогазодинамическими и колебательными процессами, в настоящее время практически не изучен [5].

Рассмотрим процесс отливки органоминерального композиционного материала на несущий воздушный буфер, образованный за счет истечения сжатого воздуха сквозь пористую форму. Траекторию движения точки О1 фронтальной поверхности струи массы в потоке воздуха можно условно разбить на три этапа (рисунок 1).

На первом этапе точка О 1 удалена от рабочей поверхности формы на расстояние S, большее h i , где h i - расстояние до верхней торцевой поверхности формы.

На втором этапе точка 01 проходит расстояние от плоскости верхней торцевой поверхности формы до точки, соответствующей началу пленочного течения воздуха, т.е. в интервале от h1 до h0.

На третьем этапе расстояние между формой и фронтальной поверхностью струи меняется в пределах от величины, соответствующей появлению пленочного течения воздуха, до расстояния соответствующего минимальной толщине буферного слоя, на котором скорость движения точки О 1 равна нулю.

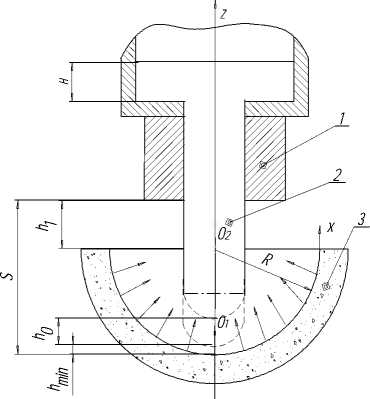
Рисунок 1. Формование органоминерального композиционного материала на несущем воздушном буфере: 1 – насадка отливочного механизма; 2 – струя материала; 3 – пористая форма.

канале дозирующего устройства:

F 2 = 8 ц o Q ( t

L i   Li )

R²  R i .

i_Z P Q² ( t ) n R i

где L 1 – длина столбика материала в цилиндре отливочного механизма, м; L 2 – длина насадки дозирующего устройства, м; R 1 – радиус поршня отливочного механизма, м; R 2 – радиус поршня дозирующего устройства , м; ζ – коэффициент местного сопротивления.

Сила, действующая на органоминеральный композиционный материал со стороны

поршня:

F = ^ ^f 32V

3       4 I

^ц 0 L 2 d²

+ P a

Движение струи на первом этапе происходит в турбулентном потоке воздуха, истекающем сквозь пористую поверхность полусферической формы. Движение центра (точка О 2 ) струи (рисунок 1) можно описать с помощью уравнения поступательного движения объекта переменной массы вида:

d2z m = Fi + F2 — F3 — mg, (1) dt2 1 2 3

где m – масса объекта, кг; F 1 – сила сопротивления встречного потока воздуха, H; F 2 – сила трения, действующая на струю органоминерального композиционного материала в канале дозирующего устройства, H; F 3 – сила, действующая на композиционный материал со стороны поршня, H.

Масса объекта, находящегося на воздушном буфере:

m = Q ( t ) p t , (2) где Q(t) - объемный расход массы, м³/с; р -плотность органоминерального композиционного материала, кг/м3; t – текущее значение времени, с.

Сила сопротивления встречного потока воздуха:

F 1 = ¹ P c n ^R2 U ОТ c , ⁽³⁾ где р _с - плотность газа, кг/м³; R c - радиус поперечного сечения струи, м; U OT – относительная скорость набегания потока воздуха; с – коэффициент гидродинамического сопротивления.

Сила трения, действующая на струю в

где d l – диаметр внутреннего канала насадки, м; V – объем струи, м3; μ0 – вязкость органоминерального композиционного материала, H·с/м²; d – внутренний диаметр цилиндра отливочного механизма, м; Р а – атмосферное давление, Па.

Совместное решение выражений (1) – (5) с учетом начальных условий позволяет определить скорость ż 1 движения точки О 2 на

первом этапе.

Рассмотрим движение точки О 2 центра массы струи на втором этапе. Уравнение движения в этом случае аналогично уравнению (1).

При движении на втором этапе можно считать, что часть струй воздуха, истекающих сквозь пористую форму, не оказывают влияния на характер движения. Поэтому необходимо учесть перераспределение расхода воздуха между питающими отверстиями формы.

Объемный расход воздуха, истекающего через отверстия формы, “перекрываемые” струей органоминерального композиционного

материала:

Q1 = Xn R! ( 2 sin y — sin ( 2 Y )) |f U_o + dz ^ , (6) где λ – коэффициент проницаемости материала

формы; R p

–

радиус формы ,м; у

деформация полуфабриката, м:

f

Y = arctg ■

R c     1

–

v ^Rp

—

z — Rc c 7

.

Объемный расход воздуха, истекающего через “открытые” отверстия формы:

Q_o = Xk R 2 u₀ ( i — 2sin y + sin ( 2 y )) .      (7)

Из уравнений (6) и (7) можно получить выражение для определения относительной скорости движения потока воздуха:

Q — Xn R 2 U o ( 2 — 2sin y + sin ( i Y )) = U + dz (₈)

Xn R ^ ( 2 sin y — sin ( 2 y ))           0 dt

После ряда преобразований уравнения (1) с учетом (8) получим выражение, решив которое с учетом начальных условий (при t = t 1 ; z = h 1 и ż =ż 1 ) можно найти скорость движения точки О 2 на втором этапе.

При достижении высоты h 0 между опорной поверхностью струи композиционного материала и рабочей поверхностью формы уста-

навливается пленочное течение воздуха, при этом скорость движения точки О 1 фронтальной поверхности струи органоминерального компо-

d2z dm 2- = Fconp. - FT + J pdAA ,    (10)

dt                 AA где dm – масса элементарного объема органоминерального композиционного материала, кг; z0 – перемещение точки О3 фрагмента органоминерального композиционного материала, м; Fсопр – сила внутреннего трения, Н; Fт – сила тяжести, действующая на элементарный объём фрагмента массы, Н.

зиционного материала гораздо меньше скорости движения воздуха в воздушном буфере [5].

Уравнение движения точки О 2 центра

масс струи на третьем этапе при граничных условиях t = t 2 ; z = h 0 :

d2z m—у = J pdA + F2 - mg - F3 , dt2 A

где p - полное абсолютное давление в газовом буферном слое, Па; А – площадь опорной поверхности объекта, м2.

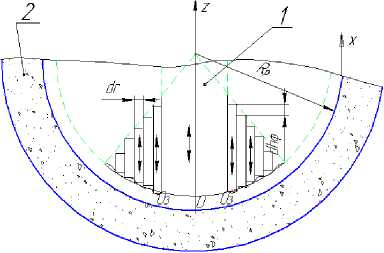
Рисунок 2. Колебания органоминерального композиционного материала при отливке на воздушный буфер: 1 – масса органоминерального композиционного материала; 2 – пористая форма.

Выражение,    описывающее поле

Выражение, описывающее поле давления среды в воздушном буфере, имеет следу-

+ 12 ^X U o R p x k

давления среды в воздушном буфере имеет следующий вид: 23

xk            xk 2          2 C p0 - px = I ~ - x0 IB +l “3--xkx0 + xkx0 I "2 +

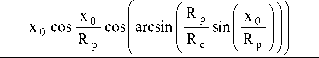
( ^{R p} к

R p • I ^x0 I

- z - R„ )cos arcsin sin I----I - R„ cc l к Rc кRp JJ J

Совместное решение уравнений (1) – (9) позволит определить расход воздуха, необходимый для полной остановки струи полуфабриката на заданной высоте.

После остановки струи органоминераль-

ного композиционного материала следует этап заполнения формы. При этом можно наблюдать колебания двух видов (рисунок 2):

• -    «поршневые» колебания, то есть колебания всей загруженной на данный момент массы;

• -    колебания типа «бегущая волна», возникающие на опорной поверхности пластической массы из-за постепенного заполнения формы и как следствие взаимное смещение соседних слоев материала.

Для описания колебательных процессов, протекающих на этапе заполнения ячейки, необходимо решить систему уравнений, включающую уравнение (9) и уравнение движения точки О 3 , принадлежащей центру фронтальной поверхности элементарного объёма органоминерального композиционного материала (рисунок 2):

ющий вид:

p- ^- p =

24 цХ xR _p ( U₀ + z ) z ³

Проинтегрировав уравнение (11) по х в пределах от 0 до х, получим выражение для определения величины суммарного воздей-

ствия на материал:

24 цХп x ² R p ( U - + Z ) J pdA =---------- г--------

A z

Подставив данное выражение в (10) и решив полученное уравнение с учётом граничных условий, определим перемещение точки О 1 .

Длительность существования “бегущей волны” определяется реологическими свойствами материала и величиной расхода газа через сечение формы.

Для решения уравнения (10) найдём силу внутреннего трения и силу тяжести, действующую на элементарный объём фрагмента полуфабриката:

F conp = 2 ^{Tn( rh}ф ^{+( r + dr )( h}Ф ^{- dh} ) ) , ⁽¹³⁾

где т - напряжение сдвига, Па; h ф - высота элементарного объёма фрагмента массы, м; dr – толщина элементарного объёма фрагмен-

та органоминерального композиционного материала, м; dh ф – разность высот элементарных объёмов фрагментов, м;

F_T = n ( 2rdr - dr ² )p gh . (14)

Процесс течения органоминерального композиционного материала удобно описывает степенной закон:

сдвига в приведенном состоянии, с-1; n(t) – индекс течения; у - скорость сдвига, с-1:

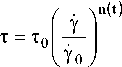
где т _о -напряжение сдвига в приведенном состоянии, Па; n(t) - индекс течения; у о — скорость

J pd АЛ =

АЛ

dz

Y=:r dr

Суммарное воздействие, оказываемое на нижнюю поверхность элементарного объёма

органоминерального композиционного материала со стороны воздушного буфера:

6 u~ R p dr ² x ² U 0 + z ) 24 ^n R p drU 0 + z ) x ²

^{( z + z} о ) 3                ^{( z + z} о ) 3        _V ²

( x

I ^rp

- x sin

( x

I ^Rp

3+2

После ряда преобразований уравнение (10) примет вид:

dm

d ² z 0 dt ²

6 цп К_р5г ² x ² ( U ₀ + z ) ^{( z + z} о ) 3

2 m-K _k ।. |_И ( t )/ , Ы' vh ф

⁽ r ^{+ dr )( h} ф

^{- dh} ф ^{)) +}

+

24 Цп К p dr ( U о + z ) | x 2

^{( z + z} о ^{) 3}        V ²

+

- 2 cos

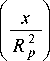
- sin

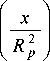
3+ 2

где K k - коэффициент консистенции.

Полагая, что перемещение z0 – пренебрежимо малая величина, разложим функцию (z + z0)-3 в степенной ряд и, учитывая лишь чле- ны до второго порядка малости включительно после упрощения получим:

d z ₀

dt ²

24 цпХ К 3 dr (

₃ p | 1 z dm V

3 U ₀ z ₀

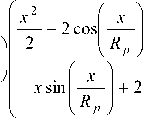
dz о dt xx

- 2 cos --- - x sin --- + 2

V ^R p J      V ^R p J

6цпХКр dr2 x2 Uо dzо z3dm dt

+ 6 цпХ 5г ² x ² U _о z _о z ⁴ dm

24 цпХ К р drU _о | _x^г z ³ dm     I 2

л

—

6 цпХ 5г ² x ² U _о +

2 n K_k

dz ₀

z ³ dm

dmdr" ⁽ t ) ^dt

n ⁽ t )

⁽ 2 rh ф

- rdh _ф + drh _ф

- drdh ф ) + g

Для решения данного уравнения необходимо определить реологические характеристики

Дифференциальное уравнение колеба-

ний объ екта на воздушном буфере:

органоминерального композиционного материала, а именно коэффициент консистенции K и индекс течения n.

Как отмечалось выше, после заполнения формы материалом в системе происходят поршневые колебания и колебания типа “бегущая волна”. Закон движения центра масс

m Z +

6 цXл³ R4 ( По +Z ) ( ho +Z )

+ mg =

Полагая, что возмущение Z - пренебрежимо малая величина, разложим функцию ( h ₀ + Z )^- 3 в степенной ряд и, учитывая лишь

члены до второго порядка малости включитель-

описывается уравнением:

d2z m—7z = I pdA - mg. dt2 A

Суммарное воздействие со стороны воздушного буфера, на объект:

6 ц^Х ( По + Z )

J рdA =-------з-------.    (22)

АА             z

Выражение для определения отклон ения от положения равновесия в воздушном буф ере можно записать следующим образом:

z = ho +Z ;Z = Z ; z = z. (23)

но, после упрощения получим:

6 цХп³ к 4 . 18 цХп ⁴к 4 п₀

m Z+      ₃ ^Р Z+ ₃ p ^О + mg = О . (25)

h30               h30

Выражение для определения толщины несущего воздушного буфера при стационарных условиях (Z = О, Z = О, Z = О ) имеет вид:

Ьо = 3

цХл ³ К4П_О mg

Перепишем (25) с учетом (26), получим:

6 цХп³ к 4 и₀     18 цХп ⁴к 4 п₀

m Z + —--- Z + — ^-p-¹ Z = О .

h30                h40

Решение данного уравнения при граничных условиях t = 0, Z = h ₀ - h min , Z = 0 имеет вид:

22 cm - n V cm - n -----— t + arctg--------- m 2             n

m

^Z =^{( h} 0 ^- h min ) e n sin

x

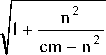
Коэффициент демпфирования:

6 цХл 3 R 4 ⁿ =----- 5----

3 . h ₀

Коэффициент жесткости:

18 ^Xn ³R 4 u₀ ^c =

.

.