Bespoke Shuffled Frog Leaping Algorithm and its Engineering Applications

Published Online March 2015 in MECS

Optimization is a process of choosing the best or alternative solution that also satisfies all the constraints, from the given set of solutions. Optimization plays a vital role in our real life too. Now a day’s most of the researchers are working and applying various optimization techniques in optimizing real world engineering design problems, management problems, and agriculture problems and almost in every sphere. Stochastic techniques are gaining much attention in Optimization as they don’t need any auxiliary knowledge about problem domain as well as their computational cost and times is also comparatively less than traditional techniques. Stochastic techniques are either inspired by some evolution, natural or biological phenomenon. Genetic Algorithm (GA) [1], Differential Evolution (DE) [2], Particle Swarm Optimization (PSO) [3], Artificial Bee Colony (ABC) [4], Shuffled Frog Leaping Algorithm (SFLA) [5] and a like falls into the category of stochastic algorithms. Their applications into various domains have already proved their efficacy to solve almost every type of optimization problems [6] – [12].

In this paper we are focusing on recently introduced Shuffled Frog Leaping Algorithm by Eusuff and Lansey, 2003 [5]. SFLA, mimics the social and natural behavior of species. SFLA is formulated on the concept of evolution of memeplexes in Frogs. SFLA combines the advantages of local search process of PSO and information exchanging of the shuffled complex evolution. Like other stochastic algorithms SFLA also bears some convergence limitations. In this study we tried to improve the convergence speed of SFLA by incorporating a new search mechanism to update the position of frogs. The proposal is named as Bespoke – SFLA.

Rest of the study is structured as follows: a brief introduction of SFLA is given in Section 2. Section 3 details the proposed Bespoke – SFLA with constrained handling procedure. Engineering design problems with mathematical models are briefed in Section 4. Parameter tuning is discussed in Section 5. Results are analyzed in Section 6. Finally, Conclusions drawn from the study are given in Section 7.

• II.    Introduction to SFLA

SFLA is a population based metaheuristic for solving discrete optimization problems. SFLA also, like others, is inspired by natural memetics. In SFLA, during the local exploitation process, the frogs use to share and inform the ideas to one another. The local searching process in each memeplexes is similar to that of PSO local search process. After exploitation process in each memeplexes the information is shuffled among different memeplexes, and thus local search process moves towards global search process (exploration). Thus, the benefits of GA as well as PSO are combined in SFLA.

SFLA consists of a population of frogs partitioned into different Memeplexes. In each memeplex a local independent search is performed by the set of frogs. This local searching process is influenced by PSO. Later on exploration or diversification is performed by exchanging information among each memeplexes. This phase is inspired by evolution process of GA. SFLA has fewer numbers of parameters to be set and is as:

• A.    No. of frogs called population size (P) or initial solutions.,

• B.    number of Memeplexes (m), and

• C.    number of frogs in each memeplex (n).

Fig. 1 depicts the searching process of SFLA in a search space.

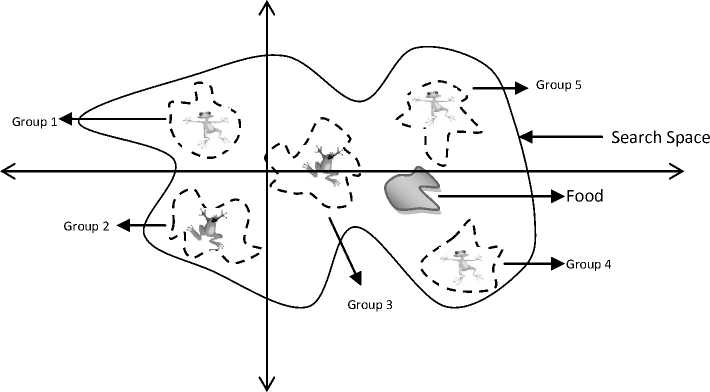
Fig. 1. Searching process in SFLA (initially locally then performs information exchange)

The steps of SFL algorithm are as follows:

• 1.    The population of frogs ( P solutions) for D – dimension is generated randomly, a frog (solution) “ i ” is represented as X i = ( x i 1 , x i 2 ,…, x iS ).

• 2.    Fitness function value is calculated for each solution (frog).

• 3.    Arrange the solutions (frogs based on their of their fitness values) in a descending order

• 4.    Then population of solutions (frogs) is divided into “ m ” number of memeplexes, each containing “ n ” frogs. Thus, P = m * n .

• 5.    Assign the frogs to the Memeplexes in such a way that first goes to the first memeplex, the second frog goes to the second memeplex,…, frog “ m ” goes to the m ^th memeplex, and frog “ m +1” goes back to the first memeplex, etc.

• 6.    Then in each memeplex, the frogs (solutions) with worst and best positions are identified.

• 7.    In each memeplex the local search is performed using the equation (1):

• 8.    The frog with the global best fitness ( X g ) is identified and global search is done using equation (2):

• 9.    Generate new frog position “ X ” randomly to replace the worst frog.

• 10.    Does the termination criteria met? If yes then stop. Else go to Step 2.

X, + 1 = X , + r x ( X b - X w )                 (1)

r is a randomly generated number between 0 and 1. If fitness value of “ X i +1 ” is superior to “ X i ”, reinstate current frog position “ X_i ” with new position “ X_{i +1}”. Else proceed to Step 8.

X , + i = X , + r x ( X g - X w )                 (2)

If “ X ₊₁” fitness value is better than the fitness value “ X ”, replace current frog position “ X ” with new position “ X +1 ”.Else go to Step 9.

X + 1 = X min + r X ( X max — X.   )             (3)

and ^X max    ⁽ x maxi, x _max 2 , ^x maxS ,.-., x max S )

• III.    Bespoke SFLA and Cosntraint Handling

In this study we tried to enhance the local search mechanism and convergence rate of basic SFLA by incorporating a scheme that is based on the best individual vector and Scaling factor at a particular generation. The updating scheme is as follows:

X + 1 = X b + F X ( X b - X w )              (4)

where F is scaling factor lies between 0 and 1 and rest of the notations are same as discussed in equation (1).

The modification is intended to keep the weighted difference vector between the best and the worst as it is in equation (1) and the remaining base vector X and randomly selected vector are replaced with the best vector and a new parameter called scaling factor.

The proposed scheme favors the exploitation since all the vectors are biased by the same direction as of best vector. As a result, the new position updating scheme has better local search ability and faster convergence rate. However, proper tuning of F is required.

Here authors would like to mention that the proposed scheme is also inspired by the behavior of social animals called human beings. Everyone in his life style would like to follow the successful peoples or their paths in order to avoid the failures in achieving their goals.

The new position update mechanism or scheme is embedded into basic SFLA as follows:

X + i

f X , + r x ( X_g - X w )

[ X_b + F x ( X b - X w )

ff a <  0.5

else

X = (x , x min       min1, min 2

, x min3

, min S

where α is a random real number lies between 0 and 1.

If the value of α is below 0.5 then the algorithm will

behave as basic SFLA otherwise bespoke – SFLA will be invoked.

Constraint Handling

In our proposal we have adopted simple constrainthandling methods. Frog positions are compared by pairs:

• •    if the position of two frogs in a memeplex are feasible, we choose the one with a better fitness function value;

• •    if the position of two frogs in a memeplex are infeasible, we choose the frog position with the lower infeasibility degree;

• •    if position of one frog is feasible and the other is infeasible, we choose the feasible one.

where       t( X ) =   (t')² + 2 т ' т ''- x ²- + (t'')² ,

2R т' = P zxx

t'' = MR

J

M = P ( L + x ²-)

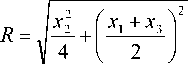
• IV. Engineering Design Problems

To evaluate the performance of the proposal a test bed of four engineering design optimization problems [12] are considered and solved.

• A. Welded Beam Design (WBD)

Minimizes the cost of the beam subject to constraints on shear stress, τ , bending stress in the beam, σ , buckling load on the bar, P c , end deflection of the beam, δ , and side constraints. This problem consists of a nonlinear objective function, five nonlinear and two linear inequality constraints. The solution is located on the boundaries of the feasible region. The ratio of feasible region to entire search space is quite small for welded beam problem. More details can be found in [13].

There are four design parameters x 1 , x 2 , x 3 and x 4 correspond to h , l , t and b variables, respectively, shown in Fig.2.

J = 2^

xx

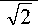
6 PL ^{o (} X ) = _r ^x 4 ^x 3 ²

5 ( X ) =

4 PL ³

Ex ³ x

Pc =

x ²

- +

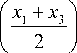
4.013 E x ₃ ² x ₄ ⁶ L ²

r

V

—

x ₃ ГЕ ) 2 L4GG J

and P = 6000lb., L = 14 in., 5_ra„ = 0.25 in., E = 30 x max

10⁶ psi, G =12 x 10⁶ psi, T, = 1, 3600 psi, o^ = max                   max

3,0000 psi, X = ( x 1 , x 2 , x 3 , x 4 )^T, 0.1 ≤ x 1 , x 4 ≤ 2.0, 0.1 ≤ x 2 , x 3 ≤ 10.

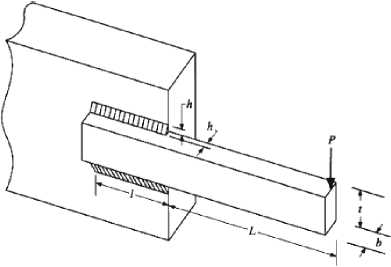
Fig. 2. The welded beam problem

B. Pressure Vessel Problem (PVP)

The objective of the PVP is to minimize the total cost of material, forming and welding of a cylindrical vessel shown in Fig.3. The nature of the problem is nonlinear objective function with a nonlinear and three linear inequality constraints. The details of the problem can be found in [13]. The mathematical model of PVP is given

as:

min f ( X ) = 1.10471 x 2 x 2 + 0.04811 x 3 x ₄(14.0 + x 2 ) x

Subject to g 1 ( X ): t ( x ) - т_ш<  0

g 2 ^{( X ):} ° ( x ) -^ max <  ⁰

g з ⁽ X ^): x ^- x 4 <  0

g ₄ ( X ) :1.10471 x 2 + 0.04811 x ₃ x 4 (14.0 + x ₂) - 5.0 <  0

g ₅( X ):0.125 - x 1 <  0

g 6 ( X ): § ( x ) -§_ < 0

g 7 ( X ): P - P_c ( x ) <  0

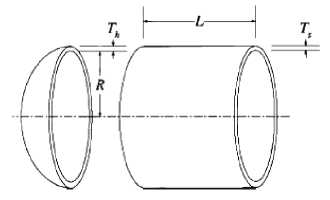
Fig. 3. The pressure vessel problem min f (X) = 0.6224x,x2x3 +1.7781x2x32 + 3.1661x 2 x4 +19.84 x 2 x3

Subject to    g 1 ( X ):- x 1 + 0.0193 x ₃<0

g₂ ( X ): - x ₂ + 0.00954 < 0

g ₃( X ): -n x 2 x ₄ -^n x ³ +1296000 < 0

g 4 ( X ): x 4 -240 < 0

where X = ( x 1 , x 2 , x 3 , x 4 )^T. The ranges of the design parameters are 0 ≤ x 1 , x 2 ≤ 99, 10 ≤ x 3 , x 4 ≤ 200.

C. Speed Reducer Design (SRD)

The objective of SRD is to minimize the weights of the speed reducer. Fig. 4 presents the outline graph of the SRD. This problem consists of 11 constraints out of which 4 are linear and 7 are nonlinear. The mathematical model is given below and the details of the SRD problem can be consulted in [13].

min f ( X ) = ( N + 2) Dd^г

Subject to

g 1 ( X ):1

g 2 ( X ):

—

-D TX < 0 71785 d ⁴

4 D ² - dD

12566( Dd ³ - d ⁴) ⁺ 5108 d²

- 1 <  0

min f ( X ) = 0.7854 xx ² ( 3.3333 x ² + 14.9334 x - 43.0394 )

g ( X ):1 -       <  0

3        D2N g 4( X): D+d-1 < 0 .

X = ( d , D , N )^T, 0.05 ≤ d ≤ 2.0, 0.25 ≤ D ≤ 1.3, 2.0 ≤ N

22     33

.     X ^ X 6 + X 7 + / .         X 6 + X 7

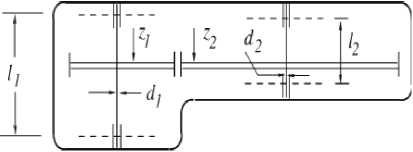
Fig. 4. The speed reducer problem g,(X):—2--1 < 0

x ₁ x ₂ ² x ₃

≤ 15.0

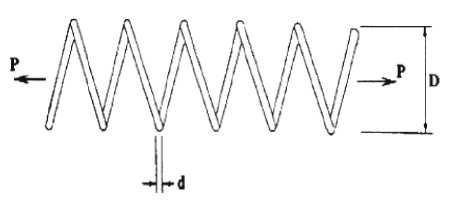
Fig. 5. The tension/compression spring problem

Subject to

g 2 ( X ):

397.5 x ₁ x ₂ ² x ₃

- 1 <  0

³ _{g 3( X ):} 1.93 x 4₄ x ₂ x ₃ x ₆

- 1 <  0

g 4 ( X ):

1.93 x ³

4 xxx

- 1 <  0

V. Parameter Settings

The parameter settings of SFLA and Bespoke-SFLA, for the fair comparison are stated in Table 1. The proposed CM-SFLA is executed in Dev C++. The population of frogs is generated using inbuilt rand () function.

Il x 2 x 3 g 5 ( X ):^l------

1/2

745 x 4 1 + 157.5 x 10⁶

Table 1. Parameterizations for test systems

110.0 x ³

³--1 <  0

Population Size of Frogs                   50

Il x 2 x 3 g б ( X ):^l------

2                    1/2

745 x 4 ¹ + 157.5 x 10 6

Memeplexes ( m )

85.0 x ³

³--1 <  0

g ₇( X ): xx ³ - 1 <  0 ⁷        40

g 8 ( X ):5 x- - 1 <  0

x ₁

g 9 ( X ): x L_ - 1 <  0

12 x

1 5v +19

g ₁₀ ( X ): ^1.5 x ^{6 + 1.9} - 1 <  0

x ₄

g ,, ( X ):l.¹ x l± 1.9 - 1 <  0

x ₅

where 2.6 ≤ x1 ≤ 3.6, 0.7 ≤ x2 ≤ 0.8, 17 ≤ x3 ≤ 28, 7.3 ≤ x4 ≤ 8.3, 7.8 ≤ x5 ≤ 8.3, 2.9 ≤ x6 ≤ 3.9, 5.0 ≤ x7 ≤ 5.5.

D. Tension/Compression Problem (TP)

The objective of TP is to minimize of the weight of the tension/compression spring revealed in Fig. 5. This problem has one linear and 3 non-linear inequality constraints with non linear objective function. Details about TP can be referred in [13].

Mathematically the minimization TP problem is formulated as:

Local Explorations iterations in each Memeplexes

Number of Function Evaluations (NFE)

D max

F (Scaling Factor)

100% of variable range

0.5

VI. Statistical Results

The simulated statistical results of four engineering design problems are compared with the results reported in the literature. The best values with the values of decision variables are for each engineering design problem are given in the Table 2 – Table 5.

We have performed 30 independent runs; where in each run 24,000 objective functions were evaluated.

We have compared the simulated results with that of available in the literature [14] [15]. [15] reached the best solution after 30,000 function evaluations, which is comparatively larger than taken by our proposal. The statistical results in terms of best values achieved are illustrated in Table 2 – Table 5. Comparative results in terms of mean, standard deviation (Std. Dev.) and best are presented in Table 6.

Table 2. Results of WBD

	Best Values (Solutions)
x 1	2.0573E-01
x 2	3.4705E+00
x 3	9.0366E+00
x 4	2.0573E-01
g 1 ( x )	-1.8190E-12
g 2 ( x )	-3.7210E-03
g 3 ( x )	0.0000E+00
g 4 ( x )	-3.4330E+00
g 5 ( x )	-8.0729E-02
g 6 ( x )	-2.3554E-01
g 7 ( x )	0.0000E+00
f ( x )	1.7249E+00

Table 3. Results of PVP

	Best Values (Solutions)
x 1	8.1250E-01
x 2	4.3750E-01
x 3	4.2098E+01
x 4	1.7664E+02
g 1 ( x )	-4.5000E-15
g 2 ( x )	-3.5880E-02
g 3 ( x )	-1.1640E-10
g 4 ( x )	-6.3363E+01
f ( x )	6.0597E+03

Table 4. Results of SRD

	Best Values (Solutions)
x 1	3.5000E+00
x 2	7.0000E-01
x 3	1.7000E+01
x 4	7.3000E+00
x 5	7.8000E+00
x 6	3.3502E+00
x 7	5.2867E+00
g 1 ( x )	-7.3915E-02
g 2 ( x )	-1.9800E-01
g 3 ( x )	-4.9917E-01
g 4 ( x )	-9.0147E-01
g 5 ( x )	0.0000E+00
g 6 ( x )	-5.0000E-16
g 7 ( x )	-7.0250E-01
g 8 ( x )	-1.0000E-16
g 9 ( x )	-5.8333E-01
g 10 ( x )	-5.1325E-02
g 11 ( x )	-1.0852E-02
f ( x )	2.9963E+03

Table 5. Results of TP

	Best Values (Solutions)
x 1	5.1583E-02
x 2	3.5419E-01
x 3	1.1439E+01
g 1 ( x )	-2.0000E-16
g 2 ( x )	-1.0000E-16
g 3 ( x )	-4.0488E+00
g 4 ( x )	-7.2948E-01
f ( x )	1.2665E-02

Table 6. Comparative Statistical Results

Problems		Optimal	SFLA	Bespoke – SFLA	COPSO	Mezura
WBD	Mean	0.724852	1.262611	1.72782	1.724800	1.777600
	Std. Dev.		1.21E-03	1.03E-02	1.20E-05	8.80E-02
	Best		1.72390	1.724852	1.724852	1.724852
PVP	Mean	6059.714335	6129.0732	6073.15	6071.013300	6379.938000
	Std. Dev.		1.54E+01	1.82E+01	1.51E+01	2.10E+02
	Best		6058.974722	6059.71583	6059.714335	6059.714300
SRD	Mean	NA	2997.1973	2996.382	2996.408500	2996.348000
	Std. Dev.		1.13E-01	1.0E-01	2.86E-02	0.00E+00
	Best		2996.46262	2996.39022	2996.372448	2996.348094
TP	Mean	0.012665	0.013301	0.01378	0.012600	0.013100
	Std. Dev.		1.78E-06	3.19E-04	1.20E-06	3.90E-04
	Best		0.0126751	0.0126691	0.012665	0.012689

• VII. Cnclusions and Future Scope

In this study we have presented a simple modification in the local searching process of Frogs in each memeplexes. The searching process is updated using new search mechanism that is based and biased on best search and secondly embedding scaling factor enhances the convergence rate of the proposal. The proposal is named as Bespoke – SFLA. Bespoke SFLA has shown a good performance on four constrained engineering design problems. We have compared the statistical results of our proposal with the basic SFLA and two algorithms results found in the literature. Our algorithm found to be capable in obtaining near optimal solutions with fewer number of function  evaluations.  This proposal could  be an alternative for solving such kind of problems. In future we will try to study the theoretical concept of the proposal and applications in multi-objective optimization problems.