Бесстрессовый алгоритм управления беговыми платформами на основе нейросетевых технологий

1. Введение. Одним из распространенных устройств имитации физических нагрузок являются активные (управляемые) беговые платформы, основанные на беговых дорожках. Они успешно применяются для опорно-двигательной реабилитации,

______РОБОТ _ ОТЕХН _ ИКА, А _ ВТОМ _ АТИЗАЦИЯ И СИСТЕМЫ УПРАВЛЕ _ НИЯ______ профессиональной подготовки, формирования определенного уровня физической нагрузки [1 – 3].

Специфика и качество функционирования активных беговых платформ напрямую зависит от используемых алгоритмов управления. При их реализации определяющую роль играет пользователь, постоянно создающий труднопрогнозируемые воздействия на систему управления, которая должна своевременно адаптироваться под действия человека и менять параметры или режимы своей работы.

Процесс формирования управляющей команды для беговой платформы основан на получении и анализе данных о движении пользователя, который осуществляется в реальном времени в процессе работы платформы. Основной проблемой в этой предметной области является запаздывание [1], так как время между изменением положения человека, реакцией системы управления и дальнейшим воздействием на положение беговой платформы может оказаться значительным. Возникающая задержка между действием пользователя и ответной реакцией беговой платформой затрудняет плавное управление и приводит к различных негативным эффектам (рывкам, резкому ускорению или торможению), что приводит к значительному стрессовому воздействию на пользователя. При комбинации беговой платформы с системами виртуальной реальности общий негативный эффект значительно усиливается [4].

Взаимодействие с платформой вызывает у пользователя определенный стресс, в котором можно выделить положительную (эустресс) и отрицательную (дистресс) формы [5]. Эустресс выражается в необходимости для человека адаптироваться к возникающим физическим нагрузкам, что приводит к формированию необходимого уровня физической подготовки. С другой стороны, наличие запаздывания и несоответствие между скоростью движения дорожки и скоростью перемещения человека приводит к появлению дополнительных отрицательных форм стресса, отвлекающих пользователя от процесса взаимодействия с виртуальной реальностью и усложняющих выполнение поставленных перед ним задач. Таким образом, под бесстрессовым алгоритмом управления беговыми платформами будем понимать алгоритм, при использовании которого система управления будет минимизировать воздействие дистресса для пользователя платформы, не оказывая влияния на эустресс. Тогда целью исследования будет разработка такого алгоритма.

Анализ исследований, в которых рассматривалось устранение дискомфорта пользователя при использовании активных беговых платформ, показал, что в настоящее время многие алгоритмы управления такими устройствами демонстрируют существенный уровень запаздывания [6 – 9]. Величина запаздывания варьируется от 0,43 до 2 секунд [1]. Так, в работе [6] с минимальным запаздыванием 0,43-0,57 при скорости в 1,2 м/с смещение пользователя может достигать 0,64 м, что для общепринятой длины таких дорожек (от 1 до 2 метров) является значительной величиной. Если оценивать средние показатели (например, системы из работ [7 – 9]), то запаздывание составляет от 1,5 до 2 секунд, а величина смещения составляет от 1 до 5 метров, что неизбежно приведет к падению с дорожки, риску для здоровья либо экстренному срабатыванию алгоритмов остановки или страховочной системы [10].

Сбор данных о действиях пользователя для принятия своевременных решений может потребовать использования дополнительного оборудования, ограничивающего свободу движений [11]. Поэтому актуальной проблемой в научном и практическом плане является разработка алгоритмов, позволяющих прогнозировать действия тренируемого и обеспечивать компенсацию запаздывания реакции беговой платформы.

Для сбора информации о движении пользователя используются различные устройства (механические и ультразвуковые датчики, устройства трехмерного позиционирования, видеокамеры). В результате анализа их особенностей [12 – 15] сформулированы следующие требования:

• -    отсутствие на пользователе оборудования, ограничивающего свободу движения;

• -    невосприимчивость к фоновому электромагнитному

излучению тренажера;

• -    область действия ≥ 1,5 м (типовая длина беговой платформы).

Анализ существующих систем отслеживания движений [16, 17] показал, что этим требованиям соответствуют только видеокамеры, если силуэт пользователя явно отличается от фона либо распознан в кадре. Работа с видеопотоком может быть организована с использованием современных моделей машинного обучения, например, MediaPipe, MoveNet, PoseNet и более новых и совершенных алгоритмов [18, 19].

С другой стороны, при использовании систем отслеживания действий человека на основе компьютерного зрения (или иных средств захвата движений) неизбежно возникает эффект запаздывания. Существует несколько факторов, снижающих быстродействие системы [20]:

• -    время на получение данных от источника (например, камер); время на передачу их в обрабатывающий терминал;

• -    обработка данных (распознавание объектов с использованием интеллектуальных алгоритмов и моделей машинного обучения);

• -    передача результата в систему управления; формирование управляющей команды;

• -    время реакции оборудования или программных инструментов на команду.

В результате запаздывание может длиться до нескольких секунд. Такой показатель быстродействия может привести к несвоевременным реакциям на действия пользователя. Например, когда человек уже находится в другой позиции и выполняет следующую операцию, либо не имеет возможности своевременно среагировать на внештатную ситуацию [8], система может послать сигнал о тех действиях, которые уже не релевантны. Основным способом уменьшения времени запаздывания является прогнозирование движений пользователя, которое может быть реализовано путем применения различных методов регрессии (начиная от обычной линейной и заканчивая более продвинутыми методами машинного обучения).

Предыдущие исследования [20 – 22] показали высокую перспективность и эффективность реализации систем управления на основе анализа текущего положения человека, в том числе, с использованием технологий компьютерного зрения. С другой стороны, разработанные ранее алгоритмы распознания модели тела человека (например, MediaPipe Objectron для сегментирования ног) не решали проблему с запаздыванием, не прогнозировали состояние пользователя, а также имели трудности с обнаружением человека при высокой скорости движений. При разработке нового алгоритма управления предлагается анализировать и прогнозировать не только положение человека на беговой платформе, но и оценивать его текущую скорость.

Использование методов машинного обучения [23], как основного инструмента поставленных задач, обосновано отсутствием необходимости формирования аналитической зависимости между исходными данными (нормированными координатами точек тела человека) и его текущей скоростью в метрических единицах, что не является тривиальной задачей, так как на эту зависимость влияет масштаб и положение модели тела в кадре, направление и угол движения человека по отношению к камере. Второй причиной использования этой группы методов является возможность сбора большого количества данных о перемещении человека с различной скоростью за счет применения двух подходов [16]:

• -    запись перемещения человека на камеру с последующим захватом ключевых точек тела; скорость человека при этом определяется путем задания фиксированного значения скорости на беговой дорожке, а также использование ручного старта/стопа для регистрации изменений ходьбы;

• -    имитационное моделирование перемещения модели человека в виртуальной среде, сохранение анимации в виде видеоряда с последующим захватом положения всех необходимых точек и текущей скорости перемещения, что позволяет за счет изменения скорости анимации варьировать скорость перемещения; для разной скорости перемещения модели могут быть заданы различные анимации (медленная или обычная ходьба, бег), кроме того анимация может быть различна для одной скорости для имитации различной походки.

• 2 . Формализация бесстрессового алгоритма управления беговыми платформами на основе нейросетевых технологий. На основе проведенного анализа можно сделать вывод о необходимости разработки бесстрессовых алгоритмов управления активными беговыми платформами с применением технологий компьютерного зрения и моделей машинного обучения для минимизации запаздывания.

Два подхода комбинируются после нормирования исходных данных о положении тела человека и объединения информации от двух источников. Количество точек определяется алгоритмами распознавания тела в кадре. Предыдущие исследования показали, что для полной реконструкции модели тела человека достаточно 18 точек [16]. Для захвата точек тела человека возможно использование различных моделей машинного обучения (MediaPipe, MoveNet), а также таких современных решений как TokenPose и их модификаций [24].

Таким образом, основной целью исследования является разработка бесстрессового алгоритма управления беговой платформой, основанного на решении задач определения текущей скорости человека за счет анализа динамики его движений в течение нескольких кадров, а также прогнозирование его скорости и положения, что позволит снизить эффект запаздывания и обеспечить своевременную реакцию системы. В качестве основного инструмента для решения задач определения скорости и ее прогнозирования предлагается использование методов машинного обучения.

Концепция предлагаемого бесстрессового алгоритма заключается в следующем: необходимо сформировать и проанализировать массивы движений пользователя (полученные

______РОБОТ _ ОТЕХН _ ИКА, А _ ВТОМ _ АТИЗАЦИЯ И СИСТЕМЫ УПРАВЛЕ _ НИЯ______ после обработки моделями машинного обучения), после чего выбрать соответствующее действие из библиотеки управляющих команд, наиболее подходящее в рамках текущего состояния человека. Для устранения запаздывания анализа и принятия решений будет производится не только по набору предыдущих кадров, но с учетом прогноза дальнейших действий человека, путем классификации и прогнозирования его движений и скорости с использованием нейросетевых технологий.

Формализуем алгоритм в виде блок-схемы (рисунок 1) и рассмотрим основные задачи, требующие решения для его практической реализации.

Алгоритм включает обязательные подготовительные операции по работе с беговой платформой [22], включая инициализацию всех необходимых программных модулей, библиотек и непосредственно подключение к драйверу управления беговой платформой, который случит посредником между программным обеспечением системы управления и установленным внутри платформы микроконтроллером. Основный цикл работы алгоритма заключается в запуске платформы, подготовке в отдельном потоке выполнения библиотек по работе с камерой (OpenCV), нейронными сетями (Keras) или алгоритмами машинного обучения (scikit-learn). Следующий шаг алгоритма реализует получение видеопотока и распознавание на нем модели тела человека с набором ключевых точек. Задавая в кадре рабочую зону, соответствующую положению беговой платформы в кадре, можно рассчитать скорость платформы s ₀ по относительному положению человека на ней, применив простейшую линейную функцию (аналогично исследованию [20]).

Используя подготовленные модели нейронных сетей или алгоритмы машинного обучения осуществляется решение двух задач: определение скорости человека по последовательности наборов точек и прогнозирование его скорости (путем обработки прогноза положения тела человека на некотором временном интервале). Так как движение человека имеет высокую степень неопределенности и хаотичности, а движение ног в процессе ходьбы то ускоряется, то замедляется, в рамках алгоритма предлагается комбинированный расчет скорости платформы с учетом корректирующих коэффициентов ( k1 , k2 , k3 ), умноженных, соответственно, на s0 , текущую скорость человека s и прогноз скорости sp , что позволяет учесть следующие ситуации:   пользователь готовится к торможению, резко останавливается, ускоряется.

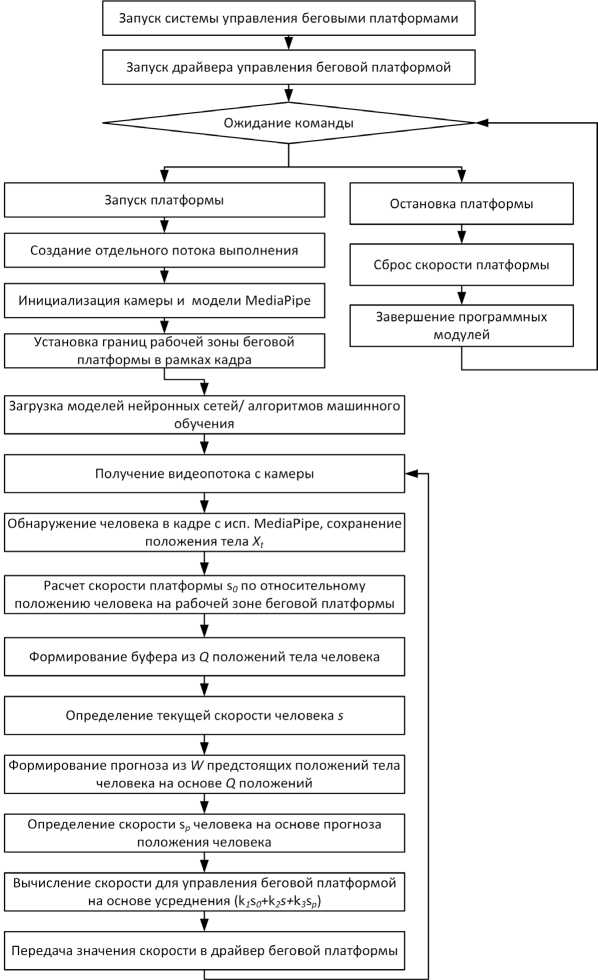
Рис. 1. Бесстрессовый алгоритм управления беговыми платформами

Варьируя корректирующие коэффициенты, возможно настроить систему управления таким образом, чтобы компенсировать недостатки линейной функции управления, а также возможные помехи и неточность работы нейронных сетей для определения скорости. Итоговое значение скорости учитывает текущую динамику движения человека и прогноз на следующий интервал в W кадров, таким образом снижая запаздывание системы управления и диапазон ее колебаний, тем самым также понижая стресс пользователя, одной из причин которого, как упоминалось выше, являются резкие ускорения и торможения платформы, приводящие к значительному изменению положения человека. Алгоритм также предусматривает остановку платформы в следующих случаях: долгое отсутствие новых кадров из видеопотока, невозможность распознавания человека в кадре, ручная остановка по завершению работы.

Таким образом, для реализации предложенного алгоритма необходимо решить две задачи: определение текущей скорости человека в зависимости от динамики перемещения; прогнозирование его скорости на основе анализа предстоящих положений тела человека.

В формализованном виде получим следующую задачу: необходимо осуществить выбор алгоритма машинного обучения A и его параметров P , который аппроксимирует регрессионную зависимость между набором положений тела человека {U_t - q _{+ 1},.U_t _ j , U_t } из Q количества замеров и его текущей скоростью s t с минимальной ошибкой E относительно реальной скорости s t .

A :{U t - q +v-U - 1 , U t } ^ S t

E ( A ) ^ min.

В качестве ошибки E используется общепринятая для регрессионных задач среднеквадратичная ошибка. Индекс t обозначает момент времени из множества дискретных интервалов от 0 до окончания работы платформы T. Каждый элемент Ut = {(xt i,Ун) I i = 0..32} содержит положения множества точек модели тела человека, нормированных относительно центра тела человека, где xt i и yti — значения координат по оси Х и Y соответственно для i точки тела человека в момент времени t .

Для успешного решения этой задачи необходимо определить оптимальный алгоритм машинного обучения, аппроксимирующий зависимость между положениями точек тела человека и его текущей скорость, что требует анализа и сравнения различных алгоритмов машинного обучения и нейронных сетей. Проведенный анализ выявил, что в этом направлении оправдано использование следующих вариантов алгоритмов [25 - 27]:

• -    регрессоры    на основе деревьев решений

(DecisionTreeRegressor):   простой в реализации и легко интерпретируемый алгоритм машинного обучения, позволяющий аппроксимировать регрессионную зависимость;

• -    регрессоры     на основе случайного леса

(RandomForestRegressor): ансамблевый метод классификации, объединяющий несколько оценщиков (деревьев решений с заданной глубиной ветвления) для повышения итоговой точности;

• -    многослойные плотные нейронные сети: простые в

реализации и универсальные аппроксиматоры;

• -    рекуррентные    нейронные сети типа LSTM:

распространенные и эффективные модели при анализе временных рядов;

• -    многослойные сверточные нейронные сети: позволяют

обобщать признаки временных последовательностей и рядов.

Помимо решения задачи (1) в рамках исследования необходимо осуществить прогнозирование скорости человека в некоторый момент времени. Формализуем этапы этой задачи, адаптировав результаты предыдущих исследований.

Пусть задан набор данных H t = {U t - q _{+ 1},..U_t - 1 , U t }, соответствующий моменту времени t е [0; T ], который обозначим как буфер положений человека с заданной длиной Q . Тогда в соответствие этому буферу H _t длиной Q можно поставить прогноз F_t длиной W : F t = {U_t+v..U_t - _{1 +} W , U t ₊ W } . Длины Q u W могут быть равными или варьироваться, учитывая, что большая длина Q упрощает прогнозирование благодаря увеличению объема данных, а большая длина W - усложняет и снижает точность прогноза. С другой стороны, слишком большая величина Q снижает влияние последних (с близкими к t индексами) элементов в общем объеме H _t имеющих большую актуальность и, следовательно, важность.

Сформулируем процесс обучения нейронной сети для прогнозирования следующим образом: заданы входные

H = { H Q , H Q _{+ 1} ,..., H T } и выходные F = { F Q , F Q _{+ 1} ,..., F T ₊ W } данные тренировочной выборки. Тогда для каждого t -го выходного вектора тренировочной выборки F _t задан входной вектор H _t соответствующий Q предшествующим набору предыдущих состояний объекта. Таким образом, на вход алгоритма машинного обучения A_F подается Q предыдущих состояний объекта, на выходе формируется W следующих состояний. Тогда задача оптимизации алгоритма A_F будет состоять в минимизации ошибки отклонения E прогнозируемых значений от их реальных значений:

AF. : H ^ F , E ( A F ) ^ min.

При решении задачи (2) также используются различные алгоритмы машинного обучения, рассмотренные выше, так как их архитектура предполагает решение обеих задач с изменением только выходного слоя.

На рисунке 2 представлена схема эксперимента, отражающая ход решения задач (1) и (2).

На первом этапе исходный кадр с камеры преобразуется в набор координат ключевых точек тела человека. Далее необходимо осуществить сбор данных о процессе перемещения человека, и сформировать Q последовательных наборов позиций точек тела человека, поступающих на вход модели нейронной сети прогнозирования. Это позволит снизить запаздывание системы управления на W FPS секунд, где FPS – частота видеоряда, получаемого с камеры.

Для определения размера W предлагается использовать следующий подход.

На первом этапе оценивается величина запаздывания О и частота FPS видеоряда с камеры. Пусть нейросетевая обработка (прогнозирование) за последние Q кадров (с учетом текущего) занимает время у , тогда общее время работы с 1 кадром обозначим как Т , Т = у + 1] FPS . Время Т всегда необходимо учитывать, так как текущий кадр требуется для осуществления прогнозирования. Тогда для компенсации запаздывания в размере О требуется осуществить прогнозирование на время О + Т .

Количество кадров, которые алгоритму необходимо прогнозировать, определяется отношением: W = (Q + V) ■ FPS .

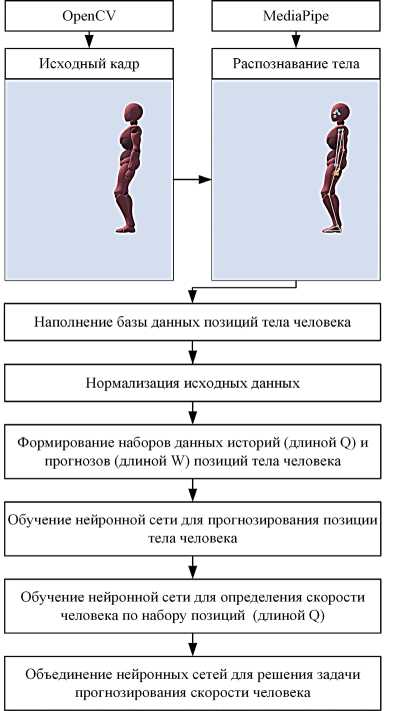
Рис. 2. Схема эксперимента по прогнозированию скорости и положения человека

Предварительные испытания разработанного алгоритма показали необходимость реализации в его рамках дополнительных преобразований исходных данных, а именно их нормализации относительно определенных точек тела человека. Это обусловлено тем, что при сборе информации человек может двигаться в различных частях изображения, поэтому использование изначальных нормированных относительно размеров кадра координат недостаточно.

Вводится дополнительное преобразование всех точек модели тела человека относительно средней позиции линии бедер (в модели MediaPipe эта зона соответствует 23 и 24 индексам), так как это наилучшим образом позволяет нормализовать точки нижних конечностей. Несмотря на то, что в базу данных записывается весь скелет человека, именно движение нижних конечностей является определяющим при определении скорости перемещения человека. Таким образом, в качестве дополнительного преобразования, направленного на повышение точности работы нейросетевых алгоритмов, может выступать фильтрация точек модели тела человека: среди 33 точек рационально выбрать только шесть, соответствующие бедрам, коленям и стопам человека. Тогда получим следующие преобразования:

U t = {( x. ,i , y. Л I i = 0..32 } ^ {( x ,i- x n , y. ,i - y n^ i = 23-28 } ,

x tⁿ

⁽ x t ,23 + x t ,24 ) n = ⁽ y t ,23 + y t ,24 ) ₂, y_{t 2}

Сокращенный и нормированный объем данных позволит исключить влияние положения человека в кадре и движений его верхних конечностей, которые не всегда соответствуют процессу перемещения.

В рамках представленного алгоритма также рассмотрим ситуацию, при которой размеры объекты наблюдения могут изменяться в процессе движения, например, когда человек удаляется или приближается к камере, что может привести к существенной разнице в величине входных данных. Поэтому для таких случаев требуется выполнить нормирование модели тела человека относительно его роста. Такое преобразование позволит игнорировать размер распознанной в кадре модели тела человека. Тогда введем следующие обозначения:

x min = min({ x_ti | x_ti ^G U_t }) - минимальное значение по оси Х среди всех точек тела человека;

x   = max({x, | x, е U,}) - максимальное значение по оси Х max                     t,i t,i         t среди всех точек тела человека;

У min = min({ y_ti | y_t i е U_t }) - минимальное значение по оси Y среди всех точек тела человека;

y max = max({ y ti | y_ti ^G U, }) — максимальное значение по оси Y среди всех точек тела человека;

Тогда:

U t ={( x t , i , У, . i )}^'

x tii" x min m xt

У I i" У min m yt

m xt = x max "  x min , my t = y max "  y min , i = 0..32.

Таким образом, дополнительные преобразования (3) и (4) позволяет повысить точность работы нейронных сетей за счет минимизации влияния положения человека в кадре и его текущих размеров.

• 3.    Сравнительный анализ нейросетевых технологий для прогнозирования движений человека. Для решения поставленных задач (1) и (2) осуществлено сравнение различных алгоритмов машинного обучения и моделей нейронных сетей с целью выявления оптимального подхода, обеспечивающего наибольшую точность. Сводная таблица итоговых оптимальных характеристик алгоритмов и моделей представлена в таблице 1.

Таблица 1. Итоговые характеристики алгоритмов машинного обучения

Модель	Описание
DecisionTreeRegres sor (DTR)	Стандартный decision tree regressor с параметром max_depth = 5
LinearRegression (LR)	Стандартная линейная регрессия с параметрами по умолчанию
Random Forest Regressor (RFR)	Стандартный регрессор случайного леса с параметрами n_estimators = 10, max_depth = 5
Сверточная нейронная сеть (CNN)	Многослойная сверточная сеть из 4 пар слоев Conv1D + BatchNormalization (количество фильтров – от 32 до 256), слоем GlobalAvgPool2D и Dense
Рекуррентные нейронные сети (LSTM)	Многослойная нейронная сеть с 2 скрытыми Dense слоями из 100 и 200 нейронов, 2 LSTM слоя (20 нейронов)
Многослойные нейронные сети (NN)	Многослойная нейронная сеть с входом из скрытого Dense слоя из 200 нейронов с функцией активацией ReLU и Dropout слоем (20% прореживание)

Архитектуры DTR, LR, RFR реализуется с использованием библиотеки scikit-learn [28], а CNN, LSTM и NN – на основе фреймворка Keras [29].

Каждая из архитектур использовалась для решения задач 1 и 2. Результаты для контрольной выборки, не участвующей в обучении или тестировании алгоритмов, представлены в таблице 2. Для первой задачи проведено 4 теста, в двух из которых прогнозированные данные не используются ( W = 0 ). В экспериментах рассматривается две величины параметров Q и W : 10 и 15 кадров, что соответствует последовательностям движений длительностью 0,4 и 0,6 секунд соответственно. Параметры выбраны в соответствии со следующим расчетом:

Величина запаздывания Q = 0,5 секунд.

Частота кадров камеры FPS = 25 .

Время нейросетевой обработки у = 0,05 секунд.

Тогда W = (0,5 + 0,05 + 0,04) ■ 25 = 14,75 , с округлением W = 15 .

Значения Q = 10 и W = 10 взяты для сравнения точности прогнозирования, а также оценки работоспособности бесстрессового алгоритма с частичной компенсацией запаздывания.

Таблица 2. Сравнение алгоритмов машинного обучения по метрике MAE

Модель	Задача определения скорости (1)				Задача прогнозирования (2)
	Q=10, W=0	Q=10, W=10	Q=15, W=0	Q=15, W=15	Q=10, W=10	Q=15, W=15
DTR	0,101	0,213	0,095	0,2	0,0033	0,0037
LR	0,496	0,489	0,489	1,47e+10	0,0034	0,0035
RFR	0,1	0,158	0,096	0,163	0,0021	0,0022
CNN	0,164	0,183	0,163	0,177	0,0101	0,0103
LSTM	0,196	0,216	0,171	0,198	0,0064	0,0069
NN	0,084	0,133	0,081	0,129	0,0044	0,0048

Для реализации бесстрессового алгоритма и проведения сравнительных испытаний использовались следующие библиотеки Python: OpenCV – для обработки видеопотока, MediaPipe для распознавания скелета человека в кадре, Keras – для формирования, обучения и применения моделей нейронных сетей, scikit-learn – для работы с алгоритмами машинного обучения. После сбора данных использовалось дополнительное преобразование (3) для нормирования координат нижних конечностей.

Общий объем собранных данных о перемещении человека с различной скоростью на активной беговой платформе составил 3495 записей для обучения и тестирования, 548 записей – для контрольной валидации. Исходные данные для обучения моделей машинного обучения сформированы в виртуальной среде Unity, что позволило фиксировать скорость и положение человека в произвольные моменты времени. Для оценки качества моделей использовалась метрика среднего абсолютного отклонения (MAE) между реальной скоростью и прогнозом. Для второй задачи было вычислено отклонение по каждой отслеживаемой точке модели тела человека, после чего определено MAE.

В первой задаче получено, что при определении скорости на основе только текущих значений положений за 10 или 15 кадров наилучшие показатели имеет модель NN. При добавлении прогнозов в размере 10 и 15 кадров наименьшую погрешность также имеет модель NN. Ближайшая по точности модель – RFR. Модель LR при Q = 15 , W = 15 не смогла корректно аппроксимировать скорость, показывая слишком высокую погрешность, непригодную для использования (ошибка достигает 1,468e+10).

Решение задачи (2) обеспечивается практически всеми алгоритмами, наиболее эффективной является модель RFR. Результат применения модели RFR для прогнозирования положения и NN – для определения скорости представлен на рисунке 3.

Рис. 3. Применение обученных моделей для прогнозирования скорости (пример 1, ходьба с последующим замедлением)

В эксперименте (рисунок 3) используется видео, полученное при захвате виртуальной сцены, в котором движется цифровая модель человека. Наблюдается определенный рост погрешности при использовании прогноза на 10 или 15 кадров, но это позволяет снизить запаздывание на 0,4 или 0,6 секунд соответственно. Оценивая погрешность в процессе движения, например, при скорости в 1 м/с, получаем достаточно высокую точность прогнозирования, причем, учитывается возможное торможение человека в процессе ходьбы (на рисунке 4 это событие началось через 15 кадров и достаточно точно было спрогнозировано). Таким образом, точность прогнозирования скорости с использованием RFR и NN составила от 91-96% (при W=0) до 90,8% (при W=15), что можно считать допустимым результатом.

Далее проведена апробация разработанного алгоритма в условиях равномерной ходьбы человека параллельно камере со средней скоростью в 1-1,5м/с. Результаты прогнозирования скорости для реальных условий представлены на рисунке 4, где отражено две стадии ходьбы, полученные результаты соответствуют ожидаемому диапазону в 1-1,5 м/с. Кроме того на правом примере в момент остановки человека нейронная сеть также корректно отражает небольшую скорость (при Q = 0 , W = 0).

Прогнозируемая скорость:                             Прогнозируемая скорость:

при Q=10, W=0: 1.68            при Q=15, W=0: 1.39     при Q=10, W=0: 0.1              при Q=15, W=0: 0.35

при Q=10, W=10: 1.01           при Q=15, W=15: 1.3     при Q=10, W=10: 0.18           при Q=15, W=15: 0.57

Рис. 4. Применение обученных моделей для прогнозирования скорости

(обычная ходьба)

Полученный результат позволяет сделать вывод о том, что нейросетевые алгоритмы прогнозирования могут использоваться для

____________ROBOTICS, AUTOM _ ATION AND CONTROL SYSTE _ MS____________ определения скорости человека с точностью выше 90% на интервале прогноза до 0,6 секунд.

• 4.    Апробация разработанного алгоритма в системе управления беговой платформой. Далее разработанное программное обеспечение используется непосредственно для управления беговой платформой. Корректирующие коэффициенты были установлены на следующие значения: k ₁ = 0,3 , k ₂ = 0,2 , k ₃ = 0,5 , таким образом, наибольший приоритет при расчете итоговой скорости отдается прогнозу s_p . Из-за необходимости обеспечения безопасности пользователя процесс тестирования был разделен на 3 этапа.

Первый этап реализован следующим образом: беговая платформа движется с фиксированной скоростью 1 м/с, система управления на основе компьютерного зрения осуществляет прогноз скорости, позволяя тем самым оценить величину отклонения. Фрагмент первого этапа представлен на рисунке 5. За счет учета всех составляющих (текущее положение, текущая и прогнозируемая скорость) итоговый расчет показывает достаточно близкие значения к реальной скорости. Здесь и далее выбраны значения Q = 10 и W = 10 , при который расчет итоговой скорости показывает более корректные и точные значения, позволяя компенсировать 0,4 секунды запаздывания.

Прогнозируемая скорость: при Q=10, W=0: 1.04 при Q=10, W=10: 0.67

Итоговый расчет: 1.02 при Q=15, W=0: 1.14 при Q=15, W=15: 0.31

Рис. 5. Применение алгоритма для прогнозирования скорости на беговой платформе (первый этап тестирования)

На втором этапе тестирования беговая платформа была запущена в режиме адаптивного управления скоростью по трекерам виртуальной реальности, закрепленным на теле человека. Параллельно выполнялась запись прогноза скорости человека на основе разработанного алгоритма (без влияния на беговую платформу). Сравнение двух подходов представлено на рисунке 6. Необходимо отметить, что между двумя алгоритмами существует определенная разница, с другой стороны, предложенный подход на основе компьютерного зрения в целом совпадает по поведению с существующим, отрабатывает замедление, ускорение и остановку пользователя. Этот этап позволил проверить адекватность определения скорости при различных сценариях поведения пользователя, что необходимо перед переходом к финальному этапу тестирования.

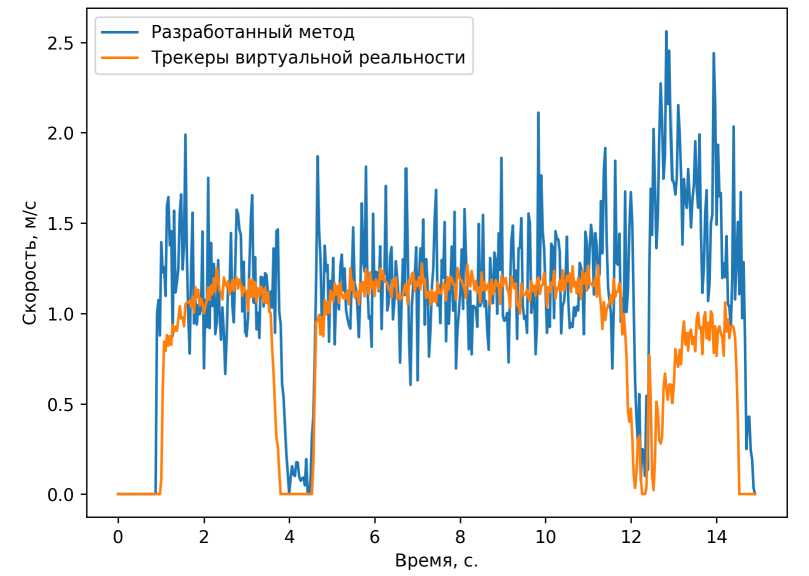
Рис. 6. Сравнение алгоритмов: разработанного и на основе трекеров виртуальной реальности (второй этап тестирования)

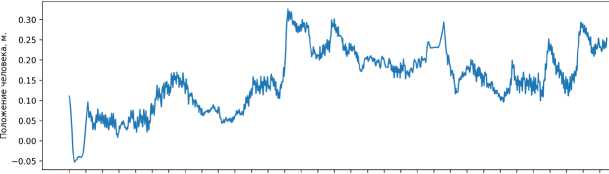
На третьем этапе тестирования (рисунок 7) для управления беговой платформой использовалось только разработанное программное обеспечение. График отражает скорость беговой платформы и положение человека на ней.

Необходимо отметить плавность и небольшую амплитуду изменения положения человека на платформе, отсутствуют моменты резкого изменения положения: среднее значение составило 0.15 метра при среднем отклонении 0.07 метра, что обеспечивает высокий комфорт пользователя при движении по платформе. Платформа также корректно останавливается при снижении скорости пользователя, причем, может осуществлять этот процесс не только на краю платформы, но и ближе к центру за счет получения нулевой скорости от нейронных сетей.

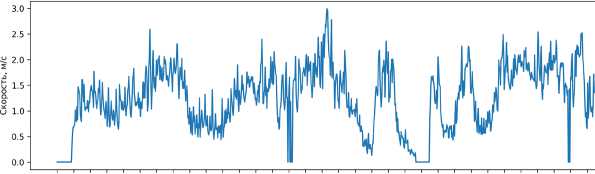
О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Время, с.

О 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 Время, с.

Рис. 7. Оценка качества работы разработанного алгоритма при управлении беговой платформой (третий этап тестирования)

Таким образом, разработанное программное обеспечение на основе бесстрессового алгоритма успешно интегрировано в систему управления беговой платформой. Разработанный алгоритм на основе комбинирования двух нейронных сетей и компьютерного зрения позволяет прогнозировать скорость человека в интервале от 10 до 15 кадров с высокой точностью (более 90%). Преимущество и новизна предлагаемого решения заключается в анализе текущего положения человека в кадре, определении текущей скорости и прогнозировании ее изменения, что в совокупности позволяет получить более точную оценку скорости, чем каждая из составляющих по отдельности. По сравнению с существующим подходом на основе трекеров виртуальной реальности предложенное решение обеспечивает сопоставимый или больший комфорт пользователя (за счет уменьшения среднего отклонения положения человека на платформе и прогнозирования его действий), а также позволяет не использовать чувствительные к помехам датчики, требующие закрепления на теле человека.

• 5.    Заключение. Поставлена задача прогнозирования скорости человека с использованием нейросетевых технологий и компьютерного зрения для минимизации запаздывания в системах управления беговыми платформами. Для ее решения разработан бесстрессовый алгоритм управления платформой, основанный на применении нейросетевых технологий для прогнозирования скорости и положения тела человека. На вход алгоритма поступает информация о положении точек тела человека, полученная при помощи технологий компьютерного зрения. Алгоритм объединяет три составляющие для получения итоговой скорости беговой платформы: анализ текущего положения человека в кадре, определение текущей скорости человека по набору последних Q кадров и прогнозирование скорости человека в интервале следующих W кадров.

В результате проведенных исследований был формализован алгоритм, включающий решение двух задач: определение положения тела человека через W количество кадров, а также определение скорости его движения по Q количеству кадров. В результате решения этих задач был снижен эффект запаздывания системы управления. В процессе исследования был проведен сбор данных о движениях человека с использованием компьютерного зрения и библиотеки MediaPipe, после чего осуществлено сравнение различных моделей нейронных сетей и алгоритмов машинного обучения для определения наиболее точного решения поставленных задач. Наилучшую точность при прогнозировании положения показал алгоритм RandomForestRegressor, а при определении скорости – многослойные нейронные сети. Получено, что при прогнозе положения тела человека в интервале длиной 15 кадров (приблизительно 0,6 секунд), скорость человека определяется с точностью более 90%. Проведены экспериментальные исследования по интеграции разработанного программного обеспечения в системы управления беговыми платформами и сравнению его с существующими решениями на основе трекеров виртуальной реальности. Из результатов экспериментов можно сделать вывод о дальнейших направлениях исследований: расширение обучающего датасета, необходимость удаления объектов окружения, перекрывающих человека (либо учет таких помех при обучении моделей), масштабирование модели тела человека, что улучшит качество работы моделей в реальных условиях. Полученные результаты могут использоваться при разработке человеко-машинных систем, функционирующих на основе компьютерного зрения и анализа действий пользователя с учетом минимизации запаздывания системы и наличия ограничений на применение нательных датчиков.