Библиотека математических функций для языка функционально-потокового параллельного программирования Пифагор

В настоящее время язык функционально-потокового параллельного программирования Пифагор [1] и его инструментальные средства [2-6] активно развиваются. Статья посвящена реализации библиотеки математических функций для языка Пифагор и иллюстрирует особенности потоковых параллельных вычислений с параллелизмом на уровне операций.

Значительная часть математических функций вычисляется с помощью рядов Маклорена. Используется как более быстрая и менее точная организация вычислений, при которой вычисляется предопределенное количество элементов ряда с заранее просчитанными коэффициентами, так и менее быстрая и более точная организация вычислений, при которой элементы ряда вычисляются динамически до достижения нужной точности.

Приближенное вычисление математических функций и их программная реализация в ряде известных языков программирования к настоящему моменту являются задачами решенными. Для языка Пифагор и его оригинальной модели вычислений задача решена впервые. Кроме этого, реализация математических функций во многих известных языках скрыта от разработчика, он может вызвать выполнение функции, но не может знать, с помощью какого метода и алгоритма происходит вычисление результата. Таким образом, описанные в статье основные принципы проектирования математической библиотеки могут быть полезны тем читателям, которым требуется решить подобную задачу для собственной вычислительной системы.

1    Быстрое приближенное вычисление математических функций на примере синуса, арксинуса и экспоненты

Ряд Маклорена для синуса имеет следующий вид.

sin ( x ) ® x - x ³/3! + x ⁵/5! - x ⁷/?! + ..., для |x | < 1. (1)

При вычислении синуса для произвольного угла = х радиан требуется привести аргумент в отрезок [ -п, п ] , используя свойство периодичности функции. Если аргумент принадлежит [ - п , -п] 2 ) U ( п( 2, п ] , он передвигается в отрезок [ - п /2, п /2 ] , при этом запоминается флаг последующего умножения результата на - 1 . Для аргумента x из [ -п) 2, п /2] вычисляется x ' = 2 x/п , формула (1) принимает следующий вид.

sin ( пx '/2 ) ® ( п) 2 ) x'- (п/ 2 ) ³ x '³/3! + ( п, 2 ) ⁵ x ^,5/5! - ..., для |x '| <  1. (2)

Для быстрого вычисления приемлемого результата берутся первые шесть слагаемых ряда и заранее вычисляются вне программного кода их численные коэффициенты, это:

П 2=1.570796326794, - ( П 2 ) 3/ 3! = - 0.645964097505, ( П 2 ) 5/ 5! = 0.079692626245, - ( П 2 ) 7 /7! = - 0.0046817541,

( П 2 ) 9/ 9! = 0.00016044118, - ( П 2/’/и! = - 0.0000035988432.

В процессе работы функции вычисляются степени аргумента, производится умножение на коэффициенты и суммирование искомой формулы. Такой алгоритм сравним с аналогичным последовательным императив- ным алгоритмом, за исключением того, что модель вычислений языка

Пифагор предполагает потенциальное параллельное выполнение всех тех операций, относящихся к одной или разным функциям, входные данные которых известны. Реализация обозначенного алгоритма средствами язы- ка Пифагор формирует следующие последовательности операторов, по- тенциально доступные для параллельного вычисления (рис. 1).

Рис. 1. Упрощенный информационно-управляющий граф функции sin

Рисунок 1 иллюстрирует то, что множество операторов одной ветви графа, например, вычисление степеней аргумента х2, х3, х5, х7 и т. д. могут быть выполнены только последовательно, т. к. нуждаются в результа- тах вычислений меньших степеней, тогда как операторы одного слоя, например «(х2,х5):*>>x7», «(0.079692626245,x5):*>>p3», «(p1,p2):+>>S1», потенциально могут быть доступны для параллельного выполнения.

При иллюстрации графа на рисунке 1 повсеместно использовано выделение вспомогательных идентификаторов, это х2, … х11, р1, … р6, S1, … S5. Программный код функции может быть реализован в таком же стиле, либо с помощью объединения формул в одно выражение. Например, вычисление искомой суммы в коде описано как «(((((p1,p2):+,p3):+,p4):+,p5):+,p6):+ >> return», при этом порядок вычисления операторов остается таким же, как на графе (рис. 1). Но, например, выделение в коде идентификатора x2 является желательным, его наличие позволяет не производить операцию x’*x’ несколько раз при вычислении степеней аргумента.

Сравнение результатов быстрого приближенного вычисления синуса в языке Пифагор и вычисления синуса с помощью вызова функции sin из библиотеки math.h в языке C представлено в таблице 1.

Таблица 1

Вычисление синуса в языке Пифагор, в языке С (библиотека math.h) и в онлайн-калькуляторе

Аргумент х	math.h	Пифагор	Калькулятор
0.2	0.198668	0.198669	0.198669
1.2	0.932039	0.932039	0.932039
3.2	–0.058373	–0.058374	–0.058374
10.0	–0.544021	–0.544021	–0.544021

Другие тригонометрические функции могут быть вычислены аналогично через их ряд Маклорена либо с помощью подстановки значений синуса в формулы приведения. При реализации библиотеки математических функций для языка Пифагор использовались формулы приведения.

При приближенном вычислении некоторых функций с помощью ряда Маклорена может наблюдаться значительное снижение точности в окрестностях отдельных точек, лежащих в области определения ряда, как правило, это 1 и –1. К таким функциям относится арксинус. Для арксинуса области определения функции и ряда совпадают, это [–1, 1], поэтому преобразование аргумента, подобное тому, которое было выполнено для синуса, не требуется. При приближенном вычислении арксинуса используется следующая формула (3), основанная на его ряде Маклорена, с вычисленными вне программного кода коэффициентами.

arcsin ( x ) ® x + 0.166666666666x 3 + 0.075x 5 + 0.044642857142x 7 +

0.030381944444x 9 + 0.022372159090x 11 + 0.017352764423x 13 +    (3)

0.01396484375x 15 + 0.011551800896x 17 + 0.009666219208x 19 +

0.008390335809x²¹ + 0.007312525873x 23 + 0.000011679728x 25 .

Если для достижения приемлемой точности синуса достаточно взять первые шесть слагаемых, то для арксинуса желательно вычислить не менее двенадцати слагаемых. Дополнительно, если х расположен в окрестностях точек 1 или –1, точность приближенной формулы значительно снижается. При реализации арксинуса для языка Пифагор при х, принадлежащем [-1,0.93)U(0.93,1], используется вспомогательная формула arcsin (x) = nJ2 - arcsin (V1 - x2 ).

При вычислении экспоненты используется следующая формула с предварительно вычисленными коэффициентами, основанная на ряде Маклорена.

e^x « 1 + x + 0.5 x ² + 0.166666666666x 3 + 0.041666666666x⁴ +

0.008333333333x 5 + 0.001388888888x 6 +

0.00019841269841x 7 , для\x | < 0.7.

Ряд Маклорена экспоненты определен на [–1, 1], но так как при быстром приближенном вычислении используется конечное малое число элементов, для достижения приемлемой точности выбрана область [–0.7, 0.7]. Область определения экспоненты — это вся числовая ось, поэтому для произвольного аргумента х используется свойство экспоненты e^a + b _ e^ae b . Аргумент х разделяется на целую и дробную части, е в дробной степени рассчитывается с помощью формулы 4, е в целой степени вычисляется перемножением констант е или 1/е, для повышения скорости вычислений при этом применяются дополнительные вычисленные вне программного кода величины, например e ⁸ = 2980.957987041726, e⁶⁴ = 6.235149080811582e+027 .

2    Точное рекурсивное вычисление математических функций на примере логарифма

Ряд Маклорена для логарифма натурального имеет следующий вид.

In ( x + 1 ) ~ x - x ²/2 + x ³/3 - x ⁴/4 + ..., для - 1 < x < 1.      (5)

Формула (5) включает большие коэффициенты, чем ряды Маклорена рассмотренных выше функций, поэтому быстрое вычисление логарифма натурального не реализовано, так как оно потребовало бы перечисления значительного количества, до нескольких сотен, возможно и тысяч, слагаемых. Вместо этого используется рекурсивное вычисление формулы (5) до достижения выбранной точности 10 ^{- 8} , в императивном языке это можно было бы реализовать с помощью цикла, в языке Пифагор циклические алгоритмы реализуются с помощью рекурсивных функций.

Область определения логарифма натурального — это множество положительных чисел, поэтому для произвольного аргумента х используется свойство логарифма натурального ln (b 10a) = ln (b) + a In (10) = In (b) + a 2.302585092994046 , где b можно выбрать так, чтобы оно подходило для вычисления ln(b) с помощью формулы (5).

Рекурсивная функция ожидает аргумент вида (число1, число2, число3), где число1 это b, число2 при первом вызове рекурсии совпадает с b, чис-ло3 — это знаменатель ряда, при первом вызове рекурсии равно единице. Одна итерация рекурсии вычисляет четыре слагаемых ряда Маклорена. Упрощенный информационно-управляющий граф функции логарифма натурального имеет следующий вид (рис. 2).

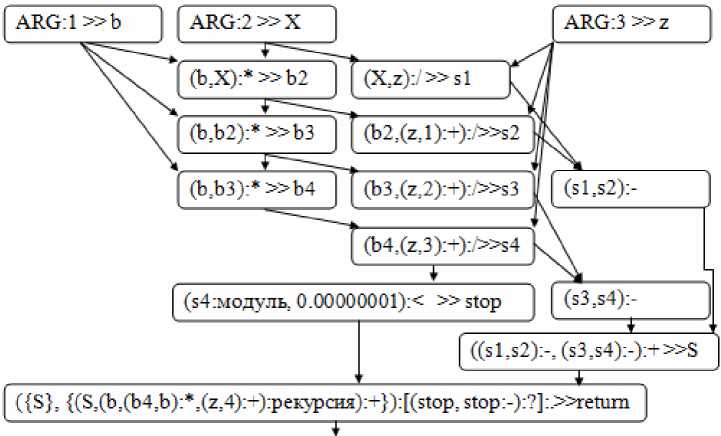
Рис. 2. Упрощенный информационно-управляющий граф функции ln

Выражения, заключенные в фигурные скобки, например {(S, (b, (b4,b):*,(z,4):+):рекурсия):+} на рисунке 2, относятся к задержанным вычислениям и будут выполняться только при истинности условия stop:-, т. е. когда четвертое слагаемое s4 в текущей итерации, взятое по модулю, оказалось больше, чем 10-8. Команды (b, (b4,b):*,(z,4):+) формируют аргумент вида (число1, число2, число3) для следующей итерации этой же рекурсивной функции. Представленное здесь рекурсивное вычисление формулы (5) можно реализовать средствами языка Пифагор и с помощью других способов организации рекурсии, но при реализации библиотеки математических функций выбран приведенный способ.

Таблица 2

Вычисление логарифма натурального в языке Пифагор, в языке С и в онлайн-калькуляторе

Аргумент х	math.h	Пифагор	Калькулятор
0.07	–2.659260	–2.659260	–2.659260
1.25	0.223144	0.223144	0.223144
200.0	5.298317	5.298317	5.298317
10500.0	9.259130	9.259131	9.259131
100000000.0	18.420681	18.420679	18.420680

Имея реализацию вычисления логарифма натурального, можно вычислить логарифм по произвольному основанию, используя свойство log a ( b ) = In ( b )/ In ( a ) , для десятичного логарифма в знаменатель подставляется вычисленная вне кода константа 2.302585092994046. Возведение в степень реализовано с помощью формулы x y = e^{y ln (} x ) .

Заключение

Задача создания математической библиотеки для языка Пифагор полностью реализована и является одной из подзадач, успешно выполненных при исполнении гранта РФФИ «Архитектурно-независимая разработка параллельных программ на основе функционально-потоковой парадигмы».

Перечисление реализованных математических функций. Модуль. Синус. Косинус. Тангенс. Котангенс. Арксинус. Арккосинус. Арктангенс. Арккотангенс. Секанс. Косеканс. Корень квадратный. Корень кубический. Округление. Округление вниз. Округление вверх. Целая и дробная части числа. Экспонента. Гиперболические синус, косинус, тангенс, котангенс. Логарифм натуральный. Логарифм десятичный. Логарифм по указанному основанию. Возведение в степень. Целая часть от деления и остаток от деления (аргументы функции могут быть числами, как целыми, так и вещественными). Выделение мантиссы и показателя степени двойки. Умножение числа на двойку в степени. Знак числа. Гиперболические ареако-синус, ареасинус, ареатангенс, ареакотангенс, ареасеканс, ареакосеканс. Возведение двойки в степень. Максимум из пары чисел. Минимум из пары чисел. Гипотенуза. Модуль разности.

Все реализованные функции включены в открытый репозиторий языка Пифагор, таким образом, разработчик может не только исполнять и просматривать их код, но и заимствовать его для создания собственных алгоритмов или альтернативной реализации математических функций.