Бифуркации стационарных многообразий, формируемых в окрестности равновесия в динамической системе резания
Автор: Заковоротный Вилор Лаврентьевич, Губанова Александра Анатольевна, Христофорова Вероника Владимировна
Журнал: Advanced Engineering Research (Rostov-on-Don) @vestnik-donstu
Рубрика: Механика
Статья в выпуске: 1 (80) т.15, 2015 года.
Бесплатный доступ
Рассмотрены проблемы нелинейной динамики процесса обработки материалов резанием. Предложена математическая модель динамической системы, учитывающая динамическую связь, формируемую процессом резания. Динамическая подсистема инструмента представлена линейной динамической системой в плоскости, нормальной к поверхности резания. На основе выполненных исследований даются рекомендации по проектированию систем, имеющих требуемые стационарные многообразия в пространстве состояния. Полученные данные позволяют сделать следующие выводы. Динамическая система резания может служить примером сложного поведения, зависящего от параметров подсистемы инструмента и представления сил в координатах состояния. Представление сил в координатах состояния зависит от множества физических процессов, сопровождающих обработку. Важно отметить, что в зависимости от моделей, взаимодействующих через процесс обработки, в окрестности равновесия могут формироваться различные критерии множества, вызывающие регулярные или нерегулярные свойства формируемой при резании поверхности.
Процесс резания материалов, динамическая система, инвариантные многообразия, бифуркации
Короткий адрес: https://sciup.org/14250121
IDR: 14250121 | УДК: 621.9: | DOI: 10.12737/10369
Текст научной статьи Бифуркации стационарных многообразий, формируемых в окрестности равновесия в динамической системе резания
Введение. Проблемы динамики процесса резания исследуются в течение последних 50 лет. При этом внимание уделялось, главным образом, двум вопросам: условиям и механизмам возбуждения автоколебаний [1–5] и анализу устойчивости процесса резания [6–10]. Довольно активно изучаются подсистемы инструмента и обрабатываемой заготовки, их взаимодействия через динамическую связь, формируемую процессом резания. Полученные в результате данные служат основой для исследования динамики процесса резания.
Для раскрытия основных свойств динамической системы можно использовать базовую динамическую модель процесса обработки, которая рассматривает упругие деформационные смещения инструмента в плоскости, нормальной к поверхности резания. При этом динамическая связь, формируемая процессом резания, представляет модель сил резания в координатах состояния системы [11–15].
В данном случае учитываются:
— нелинейная зависимость сил резания от технологических режимов [16–18];
— периодические изменения параметров динамической системы [19–21];
— закономерности формирования новых поверхностей [22–25].
При рассмотрении устойчивости системы с периодически изменяющимися параметрами, а также при формировании новых поверхностей резания используется теория Флоке [22].
В статье развиваются указанные выше представления о динамической системе резания. Основное внимание уделяется вопросам динамической самоорганизации системы, а также ее бифуркациям в параметрическом пространстве. При этом не принимаются во внимание изгибные деформационные смещения инструмента.
Базовая математическая модель. Если не принимать во внимание зависимости сил от координат состояния, то уравнение динамики процесса можно представить в виде [14].
-
d2 X, dX
m—— + h--+ cX = F (t), dt2
где m =
m
0
0, h-fr m J h1,2
h 2,1 , c = c1 , h 2,2 J L c 1,2
c 2,1
c 2,2
— соответственно матрицы инерционных, диссипативных и упру-
гих коэффициентов подсистемы инструмента; X = { X , X } T — вектор упругих деформационных смещений инструмента в плоскости, нормальной к поверхности резания; F ( t) = { F ( t ), F ( t )} T — вектор сил резания.
Упругие деформационные смещения рассматриваются в системе координат, двигающейся вдоль заготовки со скоростью движения суппорта V . Угловая скорость вращения заготовки считается постоянной. Она определяет по- стоянную составляющую скорости резания V . Поэтому в установившемся состоянии величина подачи на оборот Sp =const.
Сила резания формируется в виде суммы двух составляющих, действующих на переднюю грань инструмента
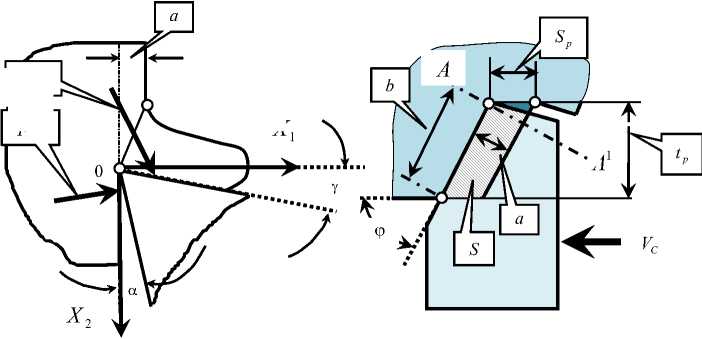
F(1) и на его заднюю грань F(2), то есть F = F(1) + F(2) (рис. 1). При заданной геометрии инструмента технологиче- ские режимы (глубина резания t и величина подачи на оборот S ) однозначно определяют ширину срезаемого слоя b и его толщину a , т. к. a = SP sin ф, а b = tp / sin ф ( ф (рис. 1) — главный угол инструмента в плане). Деформационные смещения в направлении, нормальном к плоскости (X] — X2) , не принимаются во внимание, так как деформации в этом направлении практически не вызывают изменения площади срезаемого слоя S . Кроме того, при точении обычно выполняется соотношение Sр ((tр.
X
А
Сечение А - А1
Рис. 1. Ориентация осей деформационных смещений и геометрические соотношения, определяющие формирование площади S срезаемого слоя
Cчитается, что жесткость подсистемы заготовки на порядок больше, чем жесткость инструмента, поэтому ее деформационными смещениями пренебрегаем. Заметим, что учет упругих деформационных смещений заготовки не представляет сложности. Параметры m , h и c можно определить по правилам, изложенным, например, в [11].
F(1)
ZZZ
F (2)
Механика
Главная проблема при моделировании динамической системы состоит в представлении F ( t ) = { Fv ( t ), F ( t )} T в координатах состояния. Будем следовать известным взглядам на динамическую связь, формируемую процессом резания. Отдельные элементы этих подходов изложены в выше цитированных работах. В целом, они базируются на следующих особенностях формирования сил резания:
Силы возрастают при увеличении площади срезаемого слоя S ;
-
— существуют запаздывания сил по отношению к вариациям упругих деформационных смещений [3, 6–9];
-
— они изменяются при варьировании скорости резания [4];
-
— при сближении задней грани инструмента и обработанной части заготовки имеет место непропорционально быстрое нарастание сил, действующих на заднюю грань инструмента [6, 10];
-
— существует запаздывание тангенциальных составляющих сил по отношению к их нормальным составляющим.
Кроме этого при моделировании сил используется гипотеза о неизменности ориентации сил в установившемся состоянии. Она определяется:
-
— для главной составляющей силы F (1) угловыми коэффициентами %; и %2;
-
— для силы, формируемой в области контакта задней грани с обработанной частью поверхности, — угловыми коэффициентами % (1) и % .
Коэффициенты в основном зависят от переднего угла у инструмента (угловые коэффициенты %i и %2 ) и от заднего угла (угловые коэффициенты % (1) и % 2) )• Этим свойствам соответствуют следующие представления сил резания в координатах состояния системы:
dX dX
—]-a 2[V + —Т^]3} + dt dt
F1(Xi,X2) = X1P-b •[a - У 1] + %(2)«1{[V +
-
+ % 1 1) р *. exp[ - ^d- ];
TЗ
dX dX
F2 (X 1, X 2) = % 2P- b • [ a - У 2] + % 2) ai{[V + —] -a 2[V + —] } + dt dt
-
+ %« F *-exp[ - dXFA ];
TЗ
т^+У1 = X 1; dt
T, ^7 + У1 = X1, dt где a , b — соответственно толщина и ширина срезаемого слоя, мм; T , T — постоянные времени, моделирующие запаздывание сил по отношению к деформационным смещениям, с, причем, T2)Тх; р — давление стружки на переднюю грань инструмента в кг/мм2; F(0) — сила резания, действующая на заднюю грань инструмента в состоянии равновесия, кг; T — параметр, определяющий крутизну нарастания силы, действующей на заднюю грань инструмента
(зависит от заднего угла инструмента a), мм/с; V — скорость резания; a, a2 — параметры кинетической характе- ристики процесса резания, определяющие тангенциальную составляющую силы, действующей на заднюю грань инструмента, кг·с/мм и с/мм2 соответственно.
Здесь зависимость главной составляющей силы резания от скорости аппроксимируется в соответствии с предложениями [4]. Эта составляющая также ориентирована в плоскости с помощью угловых коэффициентов % (2) и
X
2 .
Таким образом, исследованию подлежит следующая система, которая учитывает все отмеченные выше особенности динамической модели процесса резания:
<
d2 X dX dX m---t1 + h 1 + h 2 + c X. + c X = X.P" b • (a - У.) + dt 2 1,1 dt 2,1 dt 1,1 1 2,1 2
, (1) с-(0) ,
+ X F exp(-
^^^^^^
dX / dt dX dX ,
1( )п 2 2W
T3 + X 2 aX + dt a 2( V + dt ъ
d2X dX dX m--2+ + h 1 + h, , —2 + c X + c X dt2 1,2 dt 2,2 dt 1,2 1 2,2 2
(1) (0)
= Х 2 Р- b • ( а - У 2) + X 2 F exP("
^^^^^в
dX / dt dX dX
—1---) + х (2) а, [ V + —2 —a, ( V + —2)3 ];
T 21 dt 2 dt
dy
T + y = X ;
1 dt 1 1
dy
[ Г2 dt + y 2 = ^1'
Главная проблема, рассматриваемая в настоящей статье, связана с анализом притягивающих многообразий, которые формируются в окрестности равновесия системы (1), (2). Поэтому вначале рассмотрим свойства равновесия — прежде всего, условия потери его устойчивости.
Свойства равновесия системы. Точка равновесия ( X * , X * ) определяется из условия d 2 X = dX = q :
dt 2 dt
(c + v 0‘ЬЛХ + c X * = т о* b• ci + у (^/r^) -|--/(^Q, ri — n fK)31*
1,11 12,121 11 11 2
( C1 2+ X2P" b ) X * + c 2 2 X * X2P" b • a XX® F 1(0) ^[ V-a2(V )3]'
Система (4) является линейной, и она задает единственную точку равновесия, то есть при изменении параметров и внешних воздействий ветвления точек равновесия не наблюдается. Определение ее устойчивости, как известно [26], основано на линеаризованном в окрестности равновесия уравнении в вариациях относительно ( X j , Xг ) после замены Xt (t ) = X * + x t ( t ) и X 2 ( t ) = X * + x2 ( t ) . При этом учтем, что при анализе устойчивости точки равновесия X j ( t ) ^ 0 , x 2 ( t ) ^ 0 , dxx ( t ) / dt ^ 0 , dx2 ( t ) / dt ^ 0 . Тогда при выполнении этих условий справедливо
d2x , dx m + h--+ c^x = 0, dt2 Z dt z
где h2 =
h i,i -X i P bT . +X (‘) F (0)/ T з .h i2 -X 2 P bT 2 +x 2 1 ) F (0)/ T 3
h 2,1 X 1 >ai h 2,2 — X 2 >ai
, C £
C i,i +X i P b C 2,1 . TT
; x = { xx , x 2 } — вектор ва-
C i,2 +X 2 p b C 2,2 J
риаций упругих деформационных смещений.
Из (5) получаем характеристический полином линеаризованной в окрестности равновесия системы
A ( p ) =
mp 2 + ( h i,i — X i P bT i +X (1) F (0)/ T 5) p + ( c i,i +X 1 P- b ) ( h i,2 — X 2 P bT 2 +X 2) F (0)/ T 3 ) P + ( c i,2 +X 2 P" b )
(h 2,1 Xi ai) p + ci,i mP 2 + (h 2,2 — X (22) «J P + c 2,2
Механика
Очевидно, что условия потери устойчивости определяются как свойствами динамической подсистемы инструмента, так и параметрами и моделями представления сил в координатах состояния системы. В частности, если конструктивно обеспечить динамическую систему инструмента ортогональной, то при h 21 = X (2) ai система будет устойчивой, если выполнены следующие требования: h ^XiP’ b " T —X 11) F (0) / T 3, h^ 2^X 22) ai ■
Ранее показано [11], что недиагональные элементы матрицы C зависят от ориентации эллипса жесткости подсистемы инструмента в рассматриваемой плоскости. Этот случай, несмотря на некоторую его условность, подчеркивает, что главные факторы, вызывающие потерю устойчивости, связаны с формированием запаздывающих аргументов в преобразовании деформационных смещений в силы резания. Они указывают также на значение угла наклона скоростной зависимости сил по мере увеличения скорости резания.
В общем же случае главный механизм потери устойчивости при резании связан с образованием ускоряющих сил, которые формируются симметричной составляющей матрицы скоростных коэффициентов. Суммарная матрица h^ в (5) не симметрична. Следовательно, она представима в виде суммы симметричной h(0,С) и кососимметричной h£0,K) составляющих. Из (5) необходимым условием устойчивости является
[ hy-Z1P-b • T + ^ F(0)/T3)]
[h^ -0,5(x2P-T2 + x(2)«1 -X^F(0)/TJ]
[ h i,2
- 0,5(x 2P-T2 +X(2) «i —X (21) F(0)/T,)]
( h 2,2 X 2 a 1 )
> 0 ,
из которого вытекают все известные условия потери устойчивости.
Преобразованию матрицы h 0 С ) из положительно определенной в отрицательно определенную способствует увеличение:
-
— запаздывающего аргумента T ;
-
— коэффициента а,, определяющего «падающую» характеристику приращения сил при увеличении скоро-
- сти резания.
В результате система может потерять устойчивость равновесия, так как гироскопические силы, формируемые матрицей h <0’K) =
0 0,5(x2P-T2 +X(2)а,-X21)F(0) /T3)
_-0,5(x2P-T2 +X(2)а1 -X21)F(0) /T3) 0 _ , не могут стабилизировать равновесие при условии h£0,С) (0 [27, 28]. Характеристический полином (6) позволяет в параметрическом пространстве проанализировать области устойчивости. Однако нас в данной работе в основном будут интересовать условия, при которых система теряет равновесие и в его окрестности формируются различные стационарные многообразия. Проанализируем этот вопрос на примере. При этом учтем, что зачастую примеры являются более показательными, чем анализ общего уравнения.
Бифуркации стационарных многообразий в окрестности равновесия. Система (3) моделирует два взаимосвязанных колебательных контура, которые имеют два источника самовозбуждения. Один связан с запаздыванием сил резания по отношению к деформационным смещениям. Второй обусловлен существованием участка вариаций скорости (причина его возникновения — так называемый температурно-скоростной фактор), на котором увеличению скорости соответствует уменьшение сил резания. Поэтому в системе в зависимости от параметров могут существовать три стационарных состояния. Первое — асимптотически устойчивая точка равновесия. Второе — орбитально асимптотически устойчивый предельный цикл. Третье — двумерный инвариантный тор.
Рассмотрим систему, параметры динамической модели инструмента которой приведены в таблице. Достаточно малые значения элементов матрицы жесткости выбраны для того, чтобы увеличить чувствительность формируемых многообразий к изменениям параметров динамической связи в процессе резания. Продольное точение стали 20Х осуществляется четырехгранными неперетачиваемыми пластинками из Т16К6. Основные геометрические параметры инструмента: у = 6 0 , а = 20, ф = 450.
Таблица 1 Параметры динамической модели инструмента
|
m, кг х с2 /мм |
h, кгхс/мм |
с, кг/мм |
||
|
Г 0,98 - 10 -3 0 1 [ 0 0,98 - 10 -3 J |
" 30 2,0" . 2,0 12 _ |
Г 1020 25 1 . 25 108 ^ |
||
Частоты системы без взаимного влияния колебательных контуров ( h 2 = h 2 j = c 2 = С2 ] = 0 ) и динамической связи, формируемой процессом резания, соответственно равны: ю^ = 1020 Гц , to® = 332 Гц . Частоты системы с учетом динамической связи, формируемой процессом резания — ю ^ 2’ = 1540 Гц , ю (2) = 840 Гц . Давление стружки на переднюю поверхность инструмента — р = (450 - 600) кг / мм 2 . Коэффициенты ориентации силы резания в плоскости равны: Xi = 0,6, X2 = 0,8, х (1) = 1 , Хг ) = 0 , х (2) = 0,8 , x ( 2) = 0,6. Они удовлетворяют условиям нормировки, например ( X 1 ) 2 + ( X 2 ) 2 = 1 .
Чтобы варьировать основные параметры динамической характеристики процесса резания изменялись технологические режимы:
-
— скорость резания в пределах 60–160 м/мин;
-
— глубина резания в пределах 0,5–3,0 мм.
Величина подачи на оборот выбрана неизменной и равна 0,1 мм/об. Все параметры идентифицированы по правилам, изложенным в [11].
Проанализируем подробно бифуркационную диаграмму в плоскости двух параметров ( Т3 - а 1 ), приведенную на рис. 2.
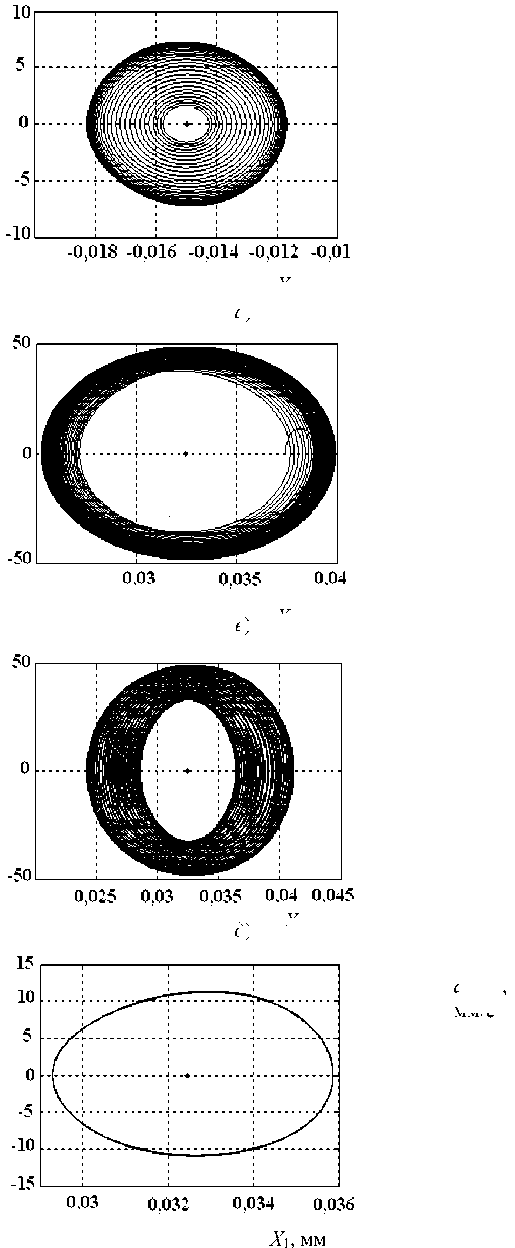
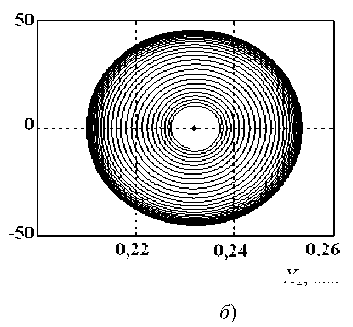
На этой иллюстрации в качестве примера показаны точки 1, 2, 3, 4, для которых на рис. 3 приведены фазовые траектории в сечениях фазового пространства. Части а, в, д, ж рис. 3 соответствуют сечению фазового пространства X dxi. Части б, г, е, з — сечению X dx2 . Все фазовые траектории сверху вниз соответствуют точкам 1, 2, 3, 4. Также ” dt 2 dt на рис. 2 приведены области D-разбиения для линеаризованного в окрестности равновесия уравнения. Они показаны пунктирными кривыми. На участках A — O — D пунктирные кривые совпадают с границами бифуркационной диаграммы, поэтому они сливаются с границами четырех областей D-разбиения:
-
— область, в которой все корни характеристического полинома расположены в отрицательной комплексной полуплоскости (A — O — D);
-
— области, в которых пара комплексно-сопряженных корней расположена в правой комплексной полуплоскости (A — O — E и F — O — D);
-
— область, в которой две пары комплексно-сопряженных корней расположены в правой комплексной полуплоскости (Е — О — F).
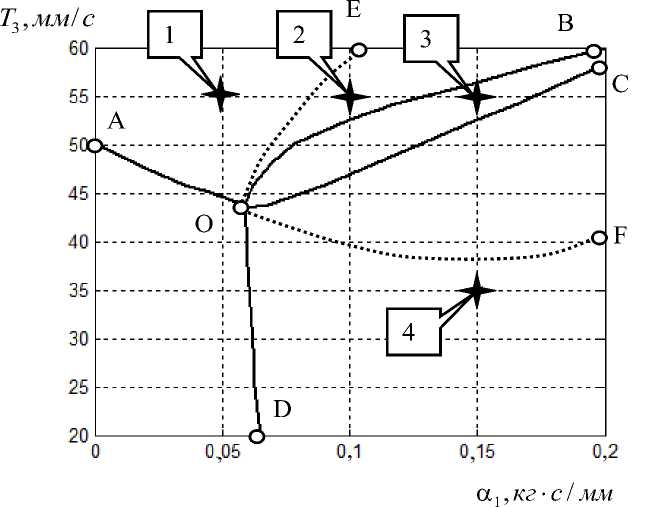
Рис. 2. Бифуркационная диаграмма в плоскости ( Т 3, а ):
Механика
A— O — D — область устойчивости равновесия; В — О — С — область формирования двумерного инвариантного тора; А — О — В — область формирования орбитально асимптотически устойчивого предельного цикла на низкой частоте; С — О — D — область формирования орбитально асимптотически устойчивого предельного цикла на высокой частоте
Как видно, границы областей D -разбиения не совпадают с границами бифуркаций инвариантных многообразий в параметрическом пространстве.
Для объяснения этого смещения границы D -разбиения и линии бифуркации перехода от предельного цикла к инвариантному тору дальше можно рассмотреть фазовые траектории, соответствующие точке 2 на рис. 2.
dx2/dt, мм/с dx2/dt, мм/с dx2/dt, мм/с dx2/dt, мм/с dx1/dt, мм/с dx1/dt, мм/с dx1/dt, мм/с dx1/dt, мм/с
в ) X 1 , мм
д ) X 1 , мм
ж )
X 1 , мм а )
X 2 , мм
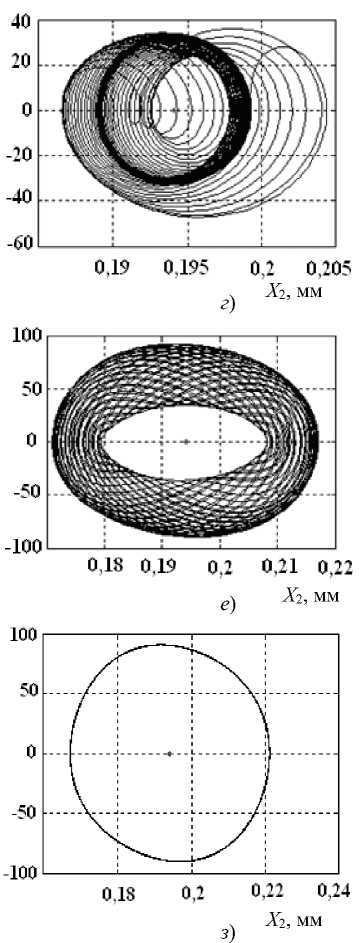
Рис. 3. Фазовые траектории системы, соответствующие четырем точкам на рис. 2: 1 ( а ), ( б ); 2 ( в ), ( г ); 3 ( д ), ( е ); 4 ( ж ), 5 ( з )
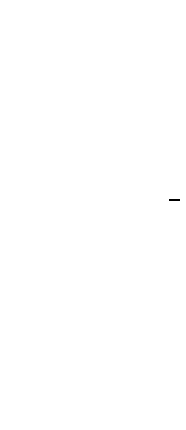
Временные диаграммы для данного случая приведены на рис. 4. Здесь хорошо видно, что двухчастотный процесс с течением времени преобразуется в одночастотный, то есть имеет место затягивание высокочастотных колебаний к низкочастотным. Аналогичная ситуация возникает и в области С — О — F. Однако здесь низкочастотный про- цесс стягивается к высокочастотному. Эти эффекты связаны с нелинейными диссипативными свойствами системы, которые учитываются в правой части системы (3).
X 1 , мм
t, c
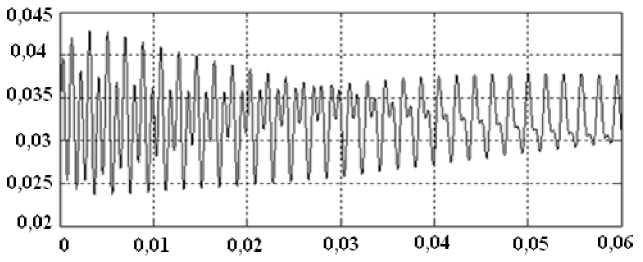
Рис. 4. Пример преобразования двухчастотного процесса в одночастотный, то есть в орбитально асимптотически устойчивый предельный цикл
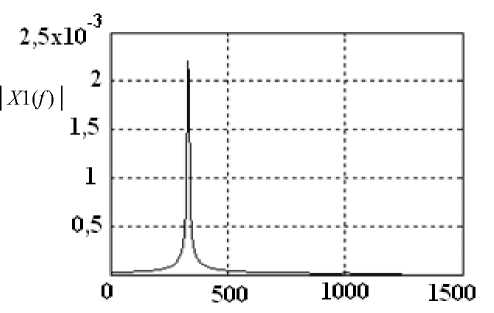
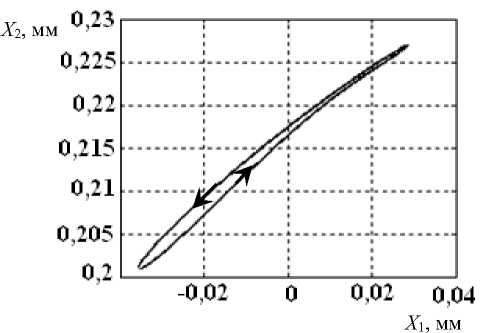
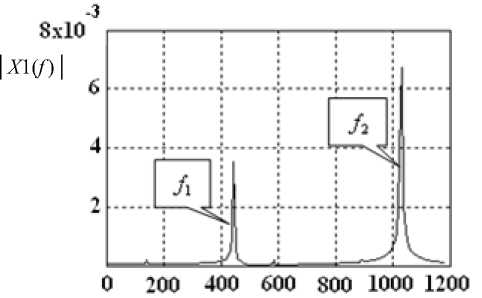
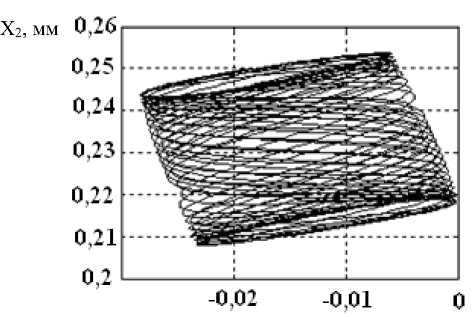
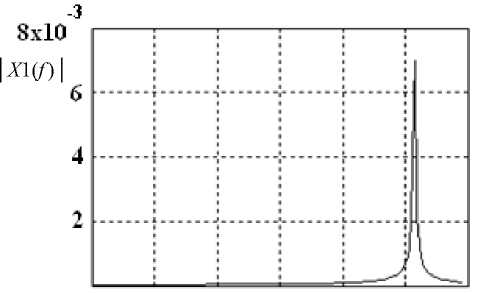
Приведем также спектральные характеристики колебаний (рис. 5, а , в , д ) для точек 2, 3, 4 на рис. 2.
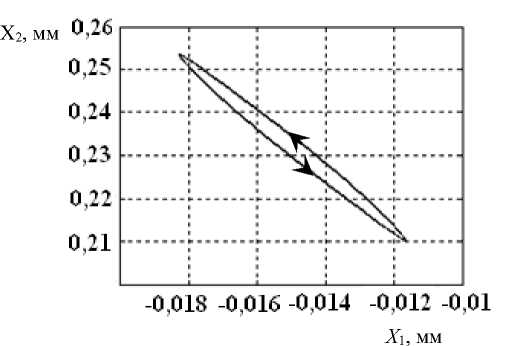
Важно подчеркнуть, что при этом меняется расположение ориентации колебаний в плоскости ( X - X ) и их размах в направлении X , в котором инструмент оставляет следы на обрабатываемой поверхности (см. рис. 5, б , г , е ). При переходе от низкочастотных автоколебаний к высокочастотным размах X соответственно уменьшается с 0,065 мм до 0,006 мм. При этом изменяется ориентация направления колебаний в плоскости ( X - X ).
Анализ влияния упруго-диссипативных параметров подсистемы инструмента на формируемые многообразия показывает, что качественно бифуркационная диаграмма остается соответствующей рис. 2. Варьирование параметров матрицы c приводит к смещениям корней характеристического полинома (6) в комплексной плоскости.
При этом корни могут сближаться. В таком случае область, в которой формируется двумерный инвариантный тор, вырождается. На формирование этой области оказывают существенное влияние недиагональные элементы матрицы жесткости. При увеличении прежде всего диагональных элементов матрицы h область устойчивости расширяется. Таким образом, при изменении параметров упругости и диссипации подсистемы инструмента происходят изменения многообразий, формируемых в окрестности равновесия системы.
Механика
Частота f , Гц
а )
б )
Частота f , Гц
X 1 , мм
в )
О 200 400 600 SOO 1000 1200
Частота f , Гц
г)
д )
е )
Рис. 5. Изменение спектров установившихся колебаний и их ориентация в плоскости ( X - X ) для точек 2 ( а ), ( б ), 3 ( в ), ( г ), 4 ( д ), ( е ) на рис. 2
Заключение. Динамическая система резания, формируемая на основе взаимодействия подсистемы инструмента с динамической связью процесса обработки, является принципиально нелинейной. В окрестности равновесия такой системы, как правило, формируются инвариантные многообразия типа предельного цикла или инвариантного тора. Параметры этих многообразий обусловлены свойствами формируемой динамической связи, зависящей от технологических режимов и от динамических свойств подсистемы инструмента. В свою очередь, известно [6, 29], что, например, стойкость инструмента обусловлена параметрами его автоколебаний. При этом в зависимости от частоты имеет место оптимальное значение автоколебаний, при которых стойкость максимальна. Кроме этого, в зависимости от ориентации параметров автоколебаний в пространстве они могут приводить к уменьшению величины шероховатости формируемой поверхности. Поэтому раскрытие механизмов образования и прогнозирование их параметров открывает путь улучшения процесса резания.
Список литературы Бифуркации стационарных многообразий, формируемых в окрестности равновесия в динамической системе резания
- Дроздов, Н. А. К вопросу о вибрациях станка при токарной обработке/Н. А. Дроздов//Станки и инструмент. -1937. -№ 12. -С. 12-17.
- Каширин, А. И. Исследование вибраций при резании металлов/А. И. Каширин. -Москва; Ленинград: АН СССР, 1944. -282 с.
- Соколовский, А. П. Вибрации при работе на металлорежущих станках/А. П. Соколовский//Исследование колебаний при резании металлов. -Москва: Машгиз, 1958. -С. 15-18.
- Мурашкин, Л. С. Прикладная нелинейная механика станков/Л. С. Мурашкин, С. Л. Мурашкин. -Ленинград: Машиностроение, 1977. -192 с.
- Альбрехт, П. Динамика процесса резания металла/П. Альбрехт//Конструирование и технология машиностроения: тр. Американского общества инженеров-механиков (ASME). -1965. -Т. 87, серия В, № 4.-С. 40-54.
- Жарков, И. Г. Вибрации при обработке лезвийным инструментом/И. Г. Жарков. -Ленинград: Машиностроение, 1987. -184 с.
- Тлустый, И. Автоколебания в металлорежущих станках/И. Тлустый. -Москва: Машгиз, 1956. -395 с.
- Кудинов, В. А. Динамика станков/В. А. Кудинов. -Москва: Машиностроение, 1967. -359 с.
- Эльясберг, М. Е. Автоколебания металлорежущих станков: теория и практика/М. Е. Эльясберг. -Санкт-Петербург: ОКБС, 1993. -182 с.
- Вейц, В. Л. Задачи динамики, моделирования и обеспечения качества при механической обработке маложестких заготовок/В. Л. Вейц, Д. В. Васильков//Станки, инструмент. -1999. -№ 6. -С. 9-13.
- Заковоротный, В. Л. Динамика процесса резания. Синергетический подход/В. Л. Заковоротный, М. Б. Флек//Ростов-на-Дону: Изд-во ДГТУ, 2006. -876 с.
- Заковоротный, В. Л. Математическое моделирование и параметрическая идентификация динамических свойств подсистемы инструмента и заготовки/В. Л. Заковоротный, Фам Динь Тунг, Нгуен Суан Тьем//Известия высших учебных заведений. Северо-Кавказский регион. -2011. -№ 2. -С. 38-46. -(Технические науки).
- Заковоротный, В. Л. Динамический мониторинг состояния процесса резания/В. Л. Заковоротный, Е. В. Бордачев, М. И. Алексейчик//Станки, инструмент. -1998. -№ 12. -С. 6-12.
- Заковоротный, В. Л. Моделирование деформационных смещений инструмента относительно заготовки при точении/В. Л. Заковоротный, Фам Динь Тунг, Нгуен Суан Тьем//Вестник Дон. гос. техн. ун-та. -2010. -Т. 10, № 7. -С. 1005-1015.
- Altintas, Y. Analytical prediction of stability lobes in milling/Y. Altintas, E. Budak//CIRP Annals. -1995. -Vol. 44. -P. 357-362.
- Balachandran, B. Non-linear dynamics of milling process/B. Balachandran//Philosophical Transactions of the Royal Society. -2001. -Vol. 359. -P. 793-820.
- Davies, M.-A. The stability of low immersion milling/M.-A. Davies, J.-R. Pratt//CIRP Annals. -2000.-Vol. 49. -P. 37-40.
- Stability prediction for low radial immersion milling/M.-A. Davies //The Journal of Manufacturing Science and Engineering. -2002. -Vol. 124. -P. 217-225.
- Prediction of regenerative chatter by modeling and analysis of high-speed milling/R.-P.-H. Faassen //The International Journal of Machine Tools and Manufacture. -2003. -Vol. 43. -P. 1437-1446.
- Corpus, W.-T. Added stability lobes in machining processes that exhibit periodic time variation. Part 1: An analytical solution/W.-T. Corpus, W.-J. Endres//The Journal of Manufacturing Science and Engineering. -2004. Vol. 126. -P. 467-474.
- Floquet, M.-G. Equations diff´erentielles lin´eaires a coefficients peridiques/M.-G. Floquet//Annales scientifiques de l'École normale supérieure. 1883. -Vol. 12 -P. 47-89.
- Заковоротный, В. Л. Параметрическое самовозбуждение динамической системы резания/В. Л. Заковоротный, Фам Тхы Хыонг//Вестник Дон. гос. техн. ун-та. -2013. -№ 5/6 (74/75). -С. 97-104.
- Nonlinear dynamics of a machining system with two interdependent delays/A. M. Gouskov //Communications in Nonlinear Science and Numerical Simulation. -2002. -Vol. 7. -P. 207-221.
- Impact of the cutting dynamics of small radial immersion milling operations on machined surface roughness/G. Peigne //The International Journal of Machine Tools and Manufacture. -2004. -Vol. 44. -P. 1133-1142.
- Szalai, R. Global dynamics of low immersion high-speed milling/R. Szalai, G. Stepan, S.-J. Hogan//Chaos: An Interdisciplinary Journal of Nonlinear Science. -2004. -Vol. 14. -P. 1069-1077.
- Меркин, Д. Р. Введение в теорию устойчивости движения/Д. Р. Меркин. -Москва: Наука, 1971.-С. 304.
- Лихаданов, В. М. О влиянии структуры сил на устойчивость движения/В. М. Лихаданов//Прикладная математика и механика. -1974. -Т. 38. -С. 246-253.
- Лихаданов, В. М. О стабилизации потенциальных систем/В. М. Лихаданов//Прикладная математика и механика. -1975. -Т. 39. -С. 53-58.
- Остафьев, В. А. Диагностика процесса металлообработки/В. А. Остафьев, В. С. Антонюк, Г. С. Тымчик//Киев: Тэхника, 1991. -С. 54-55.


