Бифуркационные переходы в динамических системах импульсных стабилизаторов напряжения

Слово «бифуркация» означает «раздвоение» и употребляется как название любого скачкообразного изменения, происходящего при плавном изменении параметров в любой системе, описываемой системой дифференциальных уравнений [1]. В данной работе изучаются бифуркации фазовых портретов систем дифференциальных уравнений на примере импульсного стабилизатора напряжения (ИСН).

• 1.    Математическая модель в ненасыщенном режиме

Запишем уравнения состояния для системы импульсного регулятора в течение двух интервалов включения: импульса DT и паузы D'T . В течение каждого интервала имеет место система линейных дифференциальных уравнений:

– в течение интервала DT _S (ключевой транзистор включен)

dx(t)/ х к—^ = A1 x (t)+B1 u;

• - в течение интервала D' T s (ключевой транзистор выключен)

dx(t)

K—^ = A 2 x (t) + B2 u, где D – коэффициент заполнения импульсов; D' = 1 -D; T - время одного периода ШИМ;

гу ) Гт л

* = x 1 = V L

V ² 7 V C 7

– вектор переменных состояния, являющийся то- ком в индуктивности и напряжением на емкости регулятора; u - входное воздействие; u = V (входное напряжение); Ai, A2 - квадратные матрицы переменных состояния силовой части регулятора, составленные на основании законов Кирхгофа:

	f- R l	) 0
A i =	L	i
	0	-
	V	rh c 7

- RL   -1 A.= L    L A 2      i        i —--

V C     rh c 7

B i , B 2 - прямоугольные матрицы коэффициентов внешнего источника (входного напряжения), составленные на основании законов Кирхгофа для его силовой части:

B i = B 2 =

' 1'

L о

V 7

Найдем решение системы (1) на интервале DT [2]

x< = A i x + B i u .

_Ф ( t ) = e A i¹

– фундаментальное решение системы (1).

t x (t ) = e ^^x 0 +J e 1^ Buds

– формула вариации произвольных постоянных, где значение матричного экспоненциала:

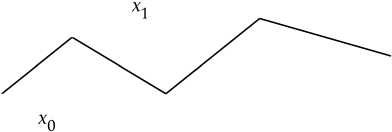
Рис. 1. График функции x n + 1

Fig. 1. Graph of the function x n _{+ 1}

x2                 X0

A² t ² A³ t ³

e A 1 ¹ « I + A₁ 1 + ^ + -^— +   .

¹        2!        3!

Рис. 2. Перенос точки покоя в начало координат

Fig. 2. Moving the rest point to the origin

Ввиду малости величины

t

V

f k

A

по абсо- )

лютной величине значение циала принимается равным

матричного экспонен-

e A 1 ¹ « I + A 1 1 или e A 1 ¹ - 1 « A i 1 ,

где I =

Желаемая точка покоя xn+1 = xn = x 0, Dn+1 = Dn = D0.                   (7)

На рис. 1 представлен график функции x n ₊ 1 . Функция x n ₊ 1 получается из функции x n (рис. 2). Подставляя значения (7) в уравнение (6) и решая его относительно x 0 , находим положение равновесия:

0 1

V

– единичная матрица.

e A ^{( 1 s} ) ® I + A 1 ( 1 - s ) .

Следовательно:

t x (1) = (I + Ai 1) xо + J[Biu + BiuAi (1 - s)] ds =

Bu A t ²

= ( I + A11) x 0 + B1 u1 + 1   1 , x (1) = (I + Ai 1) x о + Bi u1.

Решение системы (1) на интервале 0 <  1 <  DT s

^xn + 1 = ^xn = ^x 0 =

= [ I + T s ( D 0 ^A1 + D 0 ^A 2 ) ] x 0 +

+ T s ( D 0 B 1 + D 0 ^B 2 ) u ,                                 ⁽⁸⁾

x = ( D 0 B 1 + D 0 B 2 ) u

⁰      D 0 ^A 1 ⁺ D 0 ^A 2

Удобно для анализа перенести оси координат так, чтобы точка покоя (точка, в которой выходные величины регулятора являются номинальными), находилась в начале координат. Это возможно с помощью замены переменных:

примет вид x (1) = (I + Ai 1) x (0) + Bi u1.

Аналогично найдем решение системы (2) на интервале DT < 1 <  T s :

x ( 1 ) = ( I + A 1 ( 1 - DT S ) ) x ( DT S ) + B 1 u ( 1 - DT S ) .     (4)

Комбинируя уравнения (1), (2) в моменты времени 1 = DT s и D ‘ T соответственно, с учетом D ‘ T s = 1 - DT s , получаем:

x ( T s ) = [ I + T s ( DA 1 + D ' ^A 2 ) ] x ( 0 ) + + T s ( DB 1 + D ' B 2 ) u .

Перенося полученное соотношение на n + 1 интервал включения ключевого элемента, получим следующее итерационное выражение:

^x ( ( ^{n +} 1 ) T s ) = ^xn + i =

= [ I + T S ( D n^A1 + D n A 2 ) ] x n +                       (6)

+ T S ( D n B 1 + D n ^B 2 ) u .

Это уравнение является основным уравнением,

которое описывает переходный процесс системы;

это итерация значений x ( T s ) и x ( ( n + 1 ) T s ) .

^xn = ^x 0 ^{+ x}n ,    D n = D 0 ⁺ d n .                         ⁽⁹⁾

Подставляя выражения формулы (9) в уравнение (6), получим дискретное уравнение, которое описывает работу импульсного регулятора в нор-

мальном, ненасыщенном режиме:

D ‘ =1-D =l-D_n-d =Dk-d , n         n         0 n 0 n,

^x 0 ^{+ x}n + 1 =[ I ⁺ T s ⁽⁽ D 0 ⁺ d n ) ^A 1 ⁺⁽ D 0 d n ) ^A 2 ) ]^x

^x ( x 0 + x n ) + T s ( ( D 0 + d n ) B 1 + ( D 0 - d n ) ^B 2 ) u

xn + 1 =[ I + T s ( D 0 ^A 1 + D 0 A 2 ) ] x n +

⁺ T s [^{( A} 1 ^{- A} 2 ) ^x 0 ^{+( B} 1 ^{- B} 2 ) ^u ] d n ⁺

⁺ T s d n ^{( A} 1 ^- A 2 ) x n ,

где dn =- fTxn,

f ^T – матрица-строка коэффициента усиления цепи обратной связи; x n - матрица-столбец векторов состояния.

От дискретного уравнения (10) перейдем к дифференциальному уравнению с помощью аппроксимации разностного оператора дифференциальным (формула Эйлера).

dx (t) = xn+1 - xn dt        TS    ’ где TS – шаг.

В результате dx ( t )

_dt ^_( D O ^A 1 ⁺ D O A 2 ) ^{x (} t ^{) +}

⁺ [ ( A 1 ^- A ) X 0 + ( B 1 ^- B 2 ) u _] ^d ( t ) +

+ d(t)(A1 - A2 )X(t), где d (t) = -fTX (t).

Уравнение (13) – непрерывное уравнение, которое описывает работу импульсного регулятора в нормальном, ненасыщенном режиме [3].

Анализ уравнения (13) будет рассмотрен в дальнейшем.

Уравнение (13), описывающее динамику процесса в ненасыщенном режиме, может иметь положения равновесия («виртуальные»), расположенные в физически нереализуемой области или области насыщения.

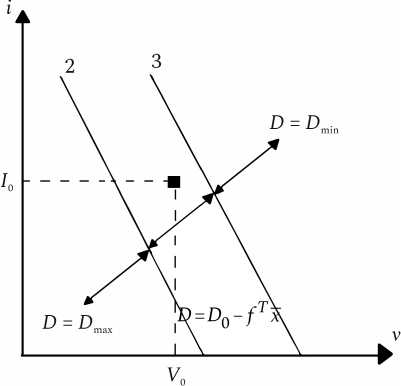
Рис. 3. Насыщенные и ненасыщенный участки ШИМ-регулятора на плоскости векторов состояния. I ₀ и V ₀ – номинальный ток (ток покоя) в индуктивности и номинальное напряжение (напряжение покоя) на конденсаторе

Рис. 3. Saturated and unsaturated sections of the PWM controller on the plane of the state vectors. I ₀ и V ₀ are the rated current (quiescent current) in the inductor, and the rated voltage (quiescent voltage) across the capacitor

2. Математическая модель в режиме насыщения

Рассмотрим выражение для коэффициента заполнения импульсов [4]

D ( t ) = D _o+ d ( t ) ,

⁰                                                   (14)

d (t ) = — fi Il — f2 Vc =— fTX, где

D sat = ^const (или D sat = D min ^или D sat = D max )* ⁽¹⁶⁾

Уравнение (15) – дискретное уравнение, которое было получено подстановкой замены (16) в уравнение (6).

От дискретного уравнения (15) перейдем к дифференциальному уравнению с помощью аппроксимации разностного оператора дифференциальным (формула Эйлера):

f^T - ( f i . f 2 ) ;

X =

ГХЛ x1

V ² 7

^ I, ^

V c

V ^C 7

;

D ₀ – коэффициент заполнения импульсов в номинальном режиме (точке покоя); f ₁ – коэффициент усиления цепи обратной связи по току; f ₂ – коэффициент усиления цепи обратной связи по на-

пряжению.

D min <  D ⁽ t ) <  D max ,

D min <  D O ^{- f X} <  D max *

Это иллюстрирует рис. 3.

X n + 1 =[ I + T s ( D sat A 1 + D sat A 2 ) ] ' n +

+ Ts ( DsatBl + DS atB2 ) », где

D S at = ¹ - D sat *

Уравнение (15) линейно, так как

dx (t)

-dt ² = [ D sat A 1 + D s at A 2 ] ^X ( t ) +

+ ( D sat B 1 + D s at B 2 ) u *

Подставим значения из формулы (7) в уравнение (15) и, решая его относительно x о , находим положение равновесия:

^x 0 =

( D sat B 1 + D sat B 2 ) u D sat A 1 + D s at A 2

3. Определение количественных соотношений

Выполним преобразования в уравнении (13):

dx^t) = (D0 A1 + D0 A2) x (t) + [(A1 - A2) x 0 + dt

+ (BA - B2 )u]d(t) + d(t)(A1 - A2)x(t), где d (x ) = -fTx = -f1 x1 - f2 x2; fT =( f1, f2) * Обозначения

.A = D 0 A ₁ + D 0 A 2 + ( A ₁ - A 2 ) x 0 f T + ( B _T - B ₂ ) uf T *

- ~г   0 A i =           ! 0-- V        R H C 7 f R L    1 ' L     L A 2 =    1       1		• ;
V C    R H - f I 0 1 x 0 = Vn ' V 0 7 f- R L A = D 0    L V 0    - R "f Rl          ^ - —   0 L — 0    - 1	C 0 1 H -	1 f -	, + D 0 R L L 1	f- R L L V C 1 1 — L 1	1 1 — L 1 R H C 7 (t V 0 о	— F1 , f 2 )
[V        R H C 7		V C    R H C 7

Тогда система примет вид dxt) = (K-1A + K1 dB) x (t), dt

	f- ( R L	+ V 0 f 1 )	( D 0 ‘+ V 0 f 2 ) 1
A =	*	L	L
	D 0	+ 1 0 f 1	I 0 f 2 R H - 1
	V	C	rh c   7
		f 1 1
B 1 =	B 2 =	L ;
		0 V 7

RL

где	f	( R l	^V 0 f 12	( D 0 + V 0 f 2 )
f L 0 1 K 1 A =			L	- L     =
0 C V 7		D 0	+ I 0 f 1	I 0 f 2 R H - 1
	V		C	R H C   7
- ( R L + V 0 f 1 )		- ( D 0	‘ + V 0 f 2 )
=       ‘ D 0 + I 0 f 1		I 0 f 2 R H - 1		;
V			H 7
	f		1 1
f L 0 1		0	L f 0	1 1
K 1 B =
0 C		1	n     -1	0
V 7		—	0 V	7
	V	C	7
Обозначим
R1 = R L + V 0 f 1 ;
N 1 = D 0 + V 0 f 2 ;
N 2 = D 0 + I 0 f 1 ;
_ I 0 f 2 R H - 1 R =             . 2      RH

B = A ₁ - A 2 =

L

0

0

-L

R H C 7

В результате получим следующую систему:

f x 1л V x 2 7	"	f- R1  - N 1' V N 2    R 2 7	+ (- f 1 x 1 - f 2 x 2 )	f 0 - 1 V	1 1" 01	x 1 V x 2 7	;
1 x 1 1 ^^2	- R 1 x 1 N 1 x 2 f 1 x 1 x 2 f 2 x 2 , = N 2 x 1 + R 2 x 2 + f 1 x 1 + f 2 x 1 x 2 .						(20)

	f R l      1 "
	LL
— -	1 1	^^^^^^
	V С   "R H C 7

(

—

I C

L

0

В результате обозначения получим систему сле-

дующего вида:

dx ( t )

-----= ( A + dB ) x ( t ).

dt

(19)

Введем нормированную матрицу K равенством:

K =

1

L

0

K ¹

0

V

_ ' L

= 0

1

C 7

;

о ^

C

;

Kdxt = ( a + dB ) x ( t ). dt

•w

Вычислим матрицу системы (20), линеаризованную в окрестности нулевой точки покоя:

	f d F 1	d F 1" 1
A =	d x 1	a x 2
	d F 2	d f 2
	Vd x 1	d x 2 7

x i = 0, x 2 = 0;

A =	- R1	- N 1'
	V N 2	R 2 7

Составим характеристическое уравнение ма-

трицы A:

| A -Xe| =

^- R i

-

X

^- N 1

N2

R2

-

X

= X ² + ( R ₁ - R ₂ ) X + N 1 N ₂ - R ₁ R ₂ = 0.

Или, что то же самое:

| A -X E | = X ² +

_r ( I f)R_H - 1

R L + V f 1 - — ^H I    ^RH

^{+ (} D 0 ⁺ V 0 ^f 2 ⁾⁽ D 0 ⁺ I 0 ^f 1 ) ^-

⁽ R L ⁺ V 0 ^f 1 ) ⁽ I 0 ^f 2 R H 1 ) R_H

x+

параметр) в системе имеет место бифуркация Андронова – Хопфа.

Введем числовые значения параметров для системы (20):

f = 0,1; R = R, + Vf = 5,75;

1          1 L 01

Найдем корни характеристического уравнения (21):

f = 1; N = D ‘ + V f = 37,9; R = 2; 2        1    0   02            L

3 75

D = b ² - 4 ac =

—

R L ⁺ V 0 ^f 1 ^-

I 0 ^f 2 R H  ¹

RH

—

N q = D ‘ + 1 f = 0,4 +-- ; V = 37,5;

2    0   01                0

RH

R = I 0 f 2 RH - 1 = 2      RH	36,5 "HT ;	D 0	= 0,6;
D 0 = 1 - D 0 = 0 4;	I 0 =	V 0 = RH	37,5 :----------------------------------------- RH

Система (20) примет следующий вид:

X 1 = - 5,75 X 1 - 37,9 x 2 - 0,1 X 1 x 2 - x 2 ,

—

;

J

RH

4 ⁽ ( D 0 + V « f 2 )( D 0 + 1 0 f 1 ) -

V

⁽ R L ⁺ V 0 ^f 1 ⁾⁽ I 0 ^f 2 R H ^- 1 ) ,

X! =- 1 1      2	Л R L <	+ V 0 f 1 -	( I 0 f 2 RH  1 ) + „ V    RH   J	) ^ J
X2 =- 1 2 2	( R L V	+ V 0 f 1 -	I 0 f 2 RH - 1 ) V    R h    J"'	) /D J

Xt2

0,4

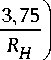
36,5

x^ +-- x ₂ + 0,1 x^ + x₁x ₂,

1 R_H 2      1   12

„ x e R , Rh e R, Rh - параметр.

Приведем достаточные условия, при выполнении которых имеет место бифуркация Андронова – Хопфа.

ц -параметр:

1) Х 1 ( ц ), X 2 ( ц ) - корни характеристического уравнения (21) оказываются чисто мнимыми при

ц = ц ₀;

• 2)    Re Х^ц ) = Re X 2 ( ц ) = 0, при Ц = Цо ;

d (Re X_t ( ц ))

• 3)    ---------- * 0 при ц = Ц о .

d ц

^ при ц = ц о система (20) обладает однопараметрическим семейством периодических решений.

Значение ц = ц о является точкой бифуркации для системы (20).

Будем считать все параметры системы фиксированными, кроме R h . Исследуем условия, при которых при изменении R_H (бифуркационный

Заключение

В результате качественного описания проблемы устойчивости и бифуркаций ИСН можно тем не менее сделать определенные выводы. Эволюция динамических систем сопровождается потерей устойчивости одними режимами функционирования и бифуркационными переходами их в новые. Эти «фазовые переходы» могут осуществляться плавно, мягко, а могут происходить скачкообразно, в виде катастроф. Строгий математический анализ устойчивости и бифуркаций позволяет сегодня практически рассматривать широкий спектр проблем, связанных с исследованиями бифуркационных переходов в динамических системах импульсных стабилизаторов напряжения. Но при этом необходимо опираться на строгие математические результаты и использовать обоснованные методы теоретического и качественного анализа.