Биомеханическая модель определения усилий мышц и связок в зубочелюстной системе человека

Изучение филогенеза, онтогенеза, анатомического строения и функций жевательного аппарата, многогранность и специфичность выполняемых им функций (захватывание, удержание пищи, ее механическая и физико-химическая обработка, © Тверье В.М., Няшин Ю.И., Никитин В.Н., 2013

Няшин Юрий Иванович, д.т.н., профессор, заведующий кафедрой теоретической механики, Пермь Никитин Владислав Николаевич, аспирант кафедры теоретической механики, Пермь образование пищевого комка, проведение его в глотку и пищевод, а также активное участие в голосо- и речеобразовании, дыхании, глотании, мимической и пластической выразительности лица) позволяют рассматривать жевательный аппарат как специализированную полимодальную многоблочную биомеханическую систему, сформировавшуюся в процессе многоэтапных преобразований и приспособлений животных организмов к условиям окружающей среды.

В жевательном аппарате четко прослеживаются клинические, анатомотопографические и морфологические признаки, отражающие влияние механической нагрузки на формирование как органных, так и тканевых структур. Это отчетливо выявляется по структуре, форме и расстановке зубов, строению периодонта, зубных рядов, височно-нижнечелюстных суставов. В зависимости от выполняемых функций четко дифференцируются форма коронок зубов (резцы, клыки, малые и большие коренные зубы), число, форма, размеры и геометрическое расположение корней зубов, форма и размеры зубных дуг (на нижней челюсти – парабола, на верхней – полуэллипс).

Силовая нагрузка, возникающая на всех этапах акта жевания, является фактором, стимулирующим и генерирующим рост, перестройку и функционирование органов и тканей жевательного аппарата. Она может быть определена по величине и направлению [8–10]. Эти данные могут быть использованы при постановке и решении задач биомеханического моделирования. Рассмотрим методы определения усилий мышц и связок.

Статически неопределенная задача определения усилий мышц и связок

Жевательный аппарат человека как специализированная биомеханическая система имеет очень сложное строение. Он состоит из малодеформируемых тел (кости черепа, в том числе верхняя челюсть и нижняя челюсть), имеющих подвижное соединение между собой (два височно-нижнечелюстных сустава); деформируемых тканей с сильно нелинейными свойствами (хрящи височно-нижнечелюстного сустава, связочный аппарат, суставная капсула); генераторов силы (жевательных мышц с сухожилиями).

Нижняя челюсть прикрепляется к черепу двумя синовиальными блоковидными височно-нижнечелюстными суставами, которые часто моделируются в виде идеальных сферических или цилиндрических шарниров; таким образом, движение челюсти в первом приближении принято считать вращательным. В действительности движения нижней челюсти являются поступательно-вращательными; нижняя челюсть и череп способны двигаться друг относительно друга. Комбинация вращения и поступательного движения позволяет делать сложные движения, что дает возможность говорить, глотать, жевать. В модели, предложенной в данной работе, височно-нижнечелюстные суставы считались идеальными сферическими шарнирами.

Взаимно независимые мышцы прилагают силы между нижней челюстью и черепом. Строение мышц не является однородным: любая мышца состоит из мышечных волокон – саркомеров. Каждое волокно имеет свою длину и угол наклона к продольной оси мышцы [11, 12]. Поэтому при моделировании скелетно-мышечной системы человека относительно внутреннего строения мышцы делается предположение об идентичности и однородности мышечных волокон, т.е. считается, что они имеют одинаковую длину (число последовательно расположенных саркомеров) и угол наклона к продольной оси мышцы. Также делается предположение об изометрическом сокращении исследуемых жевательных мышц.

Поскольку каждое волокно производит свою (хотя, в силу предположения об однородности мышцы, одинаковую по величине и направлению) элементарную силу, то принимается, что каждая мышца, изометрически сокращаясь, развивает отдельную силу по прямой линии, направленную по линии действия мышцы. Данная сила является результирующей элементарных сил, производимых мышечными волокнами. Хотя такое представление является не всегда адекватным [14], оно значительно упрощает процесс построения и исследования модели. Отметим существенную особенность: сокращение мышц и их последующее расслабление происходит под управлением центральной нервной системы.

Мышцы крепятся к костям при помощи сухожилий. Сухожилия состоят из фибрилл, которые, в свою очередь, включают в себя коллагеновые волокна. В матриксе сухожилий находятся клетки, нервные окончания и кровеносные сосуды. Нервные окончания направляют в центральную нервную систему информацию, позволяющую контролировать движения и предотвращать резкую перегрузку сухожилий.

Сухожилия с мышцами приводят в движение суставы, которые образованы двумя и более сочленяющимися костями. Что же удерживает эти суставные поверхности вместе? Связки – это структуры соединительной ткани, которые укрепляют сочленения костей, тормозят или направляют движения в суставах.

Строение связок на макроуровне не отличается от строения сухожилий [14]. Связки пронизаны нервными окончаниями, которые передают информацию о том, перегружены ли связки. В случае сильной перегрузки пучки микрофибрилл рвутся. Отличие строения сухожилий и связок проявляется на уровне коллагеновых волокон. В отличие от сухожилий, в которых коллагеновые волокна располагаются параллельно друг другу, волокна в связках имеют более хаотичные направления, хотя и здесь прослеживается предпочтительное направление волокон. Данное отличие в строении показывает, что сухожилия работают на растяжение-сжатие вдоль одного направления, проходящего через точки крепления к мышце и кости. Связки работают на растяжение-сжатие в разных направлениях в процессе функционирования суставов, которые выполняют различные виды движений. Связки и сухожилия являются пассивными элементами, не имеющими сократительных (саркомеров) элементов (как мышцы [1, 14]. Поведение связок и сухожилий можно описать законами механики. Процесс растяжения-сжатия связок и сухожилий при небольших удлинениях подчиняется закону Гука [1, 16, 17].

Для составления уравнений, описывающих статическое равновесие нижней челюсти, в качестве системы отсчета в данной работе была выбрана прямоугольная декартова система координат. Ось х направлена вперед в среднесагиттальной плоскости, перпендикулярно ей вправо направлена ось y . Ось z перпендикулярна осям х и y и направлена вертикально, т.е. перпендикулярно к окклюзионной плоскости верхних зубов. Окклюзионная плоскость определена как плоскость, проходящая через первый резец ( I 1) и первый моляр ( M l). Данная система отсчета наиболее часто употребляется при определении координат точек прикрепления мышц к черепу.

Мышечные силы ( F _i ), оканчивающиеся сухожилиями, и усилия в связках F _k ^l сбалансированы силами кусания ( F _b ) и суставными реакциями, которые возникают в правом и левом височно-нижнечелюстных суставах ( R _j ). В данной работе считаются априорно известными по величине, направлению и точке приложения статические нагрузки на нижнюю челюсть (силы кусания), т.е. здесь с силой кусания можно обращаться как с независимой величиной, варьируемой по перечисленным выше параметрам. Заданная сила кусания будет уравновешиваться мышечными силами и суставными реакциями. В качестве неизвестных переменных величин будут выступать мышечные силы и суставные реакции.

Таким образом, так как все силовые факторы в жевательной системе являются скомпенсированными, имеет место статическое равновесие нижней челюсти. Условия статического равновесия можно записать в виде уравнений (1) и (2):

N 2 N 1

Z F + Z R j + Z F k + F b = 0 . (1) i = 1 j = 1 k

N 2 N 1

Z M . + Z M j + Z M k + M b = 0 , (2) i = 1 j = 1 k = 1

где N – число рассматриваемых мышц; N ₁ – число рассматриваемых связок; R ₁ – реакция в правом височно-нижнечелюстном суставе; R ₂ – реакция в левом височнонижнечелюстном суставе. Необходимо отметить, что поскольку направление суставных реакций в височно-нижнечелюстных суставах заранее неизвестно, то реакция в каждом суставе представляется в виде трех взаимно перпендикулярных базисных компонентов. Также следует отметить, что анатомическая информация, использованная при составлении уравнений (1), (2), должна быть взята из соответствующей литературы [6].

Данная система уравнений имеет единственное решение, когда число неизвестных переменных равно шести. Шести уравнений статического равновесия нижней челюсти недостаточно, чтобы найти все неизвестные величины: мышечные силы, усилия в связках и сопутствующие им суставные реакции. Таким образом, усилия в жевательной системе человека не могут быть просто описаны уравнениями статического равновесия; получена статически неопределенная задача, для которой обычными алгебраическими методами нельзя получить однозначное решение. Соотношения между силой кусания и мышечными силами не являются единственными. Отсюда следует, что существует бесконечное число возможных комбинаций жевательных мышц, которые могут быть вовлечены для создания одной и той же силы кусания. Следовательно, необходимо сделать данную систему статически определимой. Для этого можно применять либо какие-нибудь методы снижения числа неизвестных до числа уравнений или определяющие соотношения, которые позволили бы повысить число уравнений до числа неизвестных системы, либо некоторые методы оптимизации для раскрытия статической неопределенности данной системы [14].

Мышцы являются активными органами и имеют элементы, сокращающиеся под действием нервного возбуждения. При изометрическом сокращении мышцы (длина мышцы не меняется) усилие в ней возрастает, а длина не изменяется, т.е. для описания связи усилия мышцы и изменения ее длины нельзя использовать только соотношения механики. В этом случае для построения моделей мышц используют соотношения биофизики на микро- и мезоуровнях [7, 18]. Значит, для разрешения статической неопределимости необходимо будет воспользоваться критерием оптимизации. Сухожилия и связки являются структурами, которые не обладают сократительными элементами, как мышцы, и не приводятся в возбуждение нервной системой. Их механическое поведение хорошо описывается законом Гука. Статически неопределенную упругую задачу можно решить различными методами раскрытия неопределенности теории упругости (соотношения совместности деформации, теоремы Кастильяно, Менабреа) [11], при этом потенциалы сил или перемещений являются положительно определенными квадратичными формами неизвестных усилий мышц, связок, реакций и внешних нагрузок [5]. Условия минимума в соответствующем принципе позволяют выразить усилия в связках в виде линейных функций оставшихся величин в уравнениях (1) и (2). Эти функции будут использованы в качестве дополнительных ограничений для дальнейшего решения задачи. Для нахождения оставшихся неизвестных рассмотрим другой подход.

Будем использовать путь раскрытия статической неопределимости системы уравнений для нахождения усилий в мышцах на основе оптимизации. Метод оптимизации позволяет получить единственное решение системы без выравнивания числа уравнений и неизвестных или каких-либо других видоизменений системы. Оптимизация – это математический метод для решения статически неопределимых систем уравнений, где используется критерий оптимизации – целевая функция, которая подвергается набору ограничений. Целевая функция является математическим выражением; она описывает некоторое оптимальное состояние рассматриваемой системы. Целевая функция подвергается минимизации или максимизации и подчиняется ряду ограничений в форме неравенств или равенств, которыми обычно являются уравнения статического равновесия системы.

Существует целый ряд целевых функций, с помощью которых производится решение статически избыточных систем уравнений. Одной из первых работ, в которой использовался метод оптимизации, была работа [12]. В данном исследовании находился минимум суммы модулей контактных сил в височно-нижнечелюстных суставах. Позже было показано, что данный критерий дает неудовлетворительные результаты в сравнении с экспериментальными данными [1]. В дальнейшем были сформулированы четыре физиологически обоснованных критерия оптимизации для поиска усилий мышц в нижних конечностях человека при ходьбе [17]. В первом критерии минимизировалась сумма усилий мышц, во втором – сумма квадратов усилий мышц. В качестве третьего критерия был использован критерий оптимизации, берущий за основу идею поиска минимального значения напряжения для мышцы с наибольшим напряжением, что приводит к наиболее равномерному возможному распределению усилий в группе мышц. Четвертый критерий был связан с предыдущим, но использовалось возведенное в квадрат минимальное значение напряжения для мышцы с наибольшим напряжением. Сравнение с данными электромиографического исследования показало, что при ходьбе наиболее достоверные результаты дает четвертый критерий. Для нахождения усилий мышц зубочелюстной системы в последнее время стали применять третий критерий. Применимость и работоспособность данного критерия была подтверждена в работах [13, 15, 16].

Идея данного критерия состоит в следующем. В случае, когда жевательная система развивает определенную по направлению (желаемую) силу кусания, количество возможных вариантов вовлечения жевательных мышц в процесс кусания ограничивается. Когда величина силы кусания увеличивается, область возможных вариантов вовлечения каждой мышцы в создание данной силы уменьшается. Уменьшение происходит из-за неспособности отдельных мышечных элементов производить силы, которые превышают максимальную мышечную силу данного элемента. Когда достигается максимальная сила кусания, ограниченная область мышечных вовлечений сокращается до единственного варианта.

Определим вектор значений мышечных сил X = {F1,F2,...,FN} и функции F f (X) = —г—, где г е[1, 2, .„, N ] и F(    - максимальная мышечная сила г-й

, i ,max мышцы, которая определяется как

F = КА..

• i ,    max           i ^,

где K – удельная мышечная сила, определенная экспериментально для того типа мышц, к которому относятся мышцы зубочелюстной системы, K = 37 Н - см^-2 [1]; A i - физиологическое поперечное сечение i -й мышцы.

Определим множество Q, образованное теми значениями X, при которых выполняются уравнения равновесия (1) и (2). Тогда требуется найти точку X* gQ (значения усилий мышц), для которой max f (X*) = min max f (X).                     (4)

;[1,2, . , N ] i ' X gQ i g [1,2, . , N ] i ^V '

Из вида целевой функции следует, что необходимо осуществлять поиск минимума среди континуума максимальных значений (задача на минимакс). Целевая функция для данной задачи является дискретной функцией номеров мышц. Но данная дискретная функция может быть преобразована в линейную целевую функцию (5) с N дополнительными линейными ограничениями (6) и (7).

Введем функцию p ( X ) = i max f ( X ) . Очевидно, значение максимума принадлежит ограниченной области 0 <  р < 1. Тогда будем решать следующую задачу.

Найти такой вектор усилий X*, при котором достигается min р (X),(5)

XgQ v 7

при ограничениях f (X )< р,(6)

0 < р <1,(7)

где i g [ 1, 2, .., N ].

Таким образом, от первоначальной дискретной задачи оптимизации с шестью ограничениями осуществляется переход к линейной задаче оптимизации, в которой целевая функция уравнения (5) должна быть минимизирована, удовлетворяя условиям N + 6 линейных ограничений уравнений (1), (2) и (6), (7) с двумя дополнительными условиями:

• 1.    Мышечная сила должна быть больше или равняться нулю. Данное ограничение обусловлено следующим обстоятельством: с точки зрения механики сухожильно-мышечные комплексы следует рассматривать как односторонние связи, так как они способны сопротивляться растяжению и, подобно гибким нитям, выключаются из работы при появлении в них сил осевого сжатия.

• 2.    Можно использовать экспериментальные данные работы [13] о том, что суставные реакции по оси x должны действовать в заднем направлении; суставные реакции по оси z должны действовать в нижнем направлении. Данное ограничение может быть использовано, потому что при кусании наибольшее число мышц действует вперед и вверх, таким образом, суставная реакция должна противодействовать мышечным силам, чтобы поддерживать статическое равновесие. Это ограничение не является обязательным.

Целевая функция (5) ограничена сверху, а ограничения (1), (2) и (6) линейны. Поскольку переменные задачи заданы на пересечении замкнутого отрезка, плоскости и полуплоскости (выпуклые множества), то ввиду линейности ограничений, а значит, их непрерывности, область, заданная ограничениями, является выпуклой и замкнутой [2]. Такая задача является классической задачей линейного программирования и имеет единственное решение [2]. Поэтому задача может быть решена симплекс-методом для линейного программирования.

Окончательно образом:

найти

решаемая

задача может быть сформулирована следующим

min ц ( X )

XeQ при ограничениях

N         2

Z F i x + Z R j x + Z F l . + F b . = 0.

i=1          j=1

N         2

Z F i y + Z R j y + Z F l y + ^Fb , = 0.

i=1          j=1

N         2

Z F i z + Z R j z + Z F l z + F b z = 0.

i=1          j=1

N          2

Z M i x ⁺ Z M j x ⁺ Z M k . ⁺ M b x = 0.

i=1            j=1

N          2

Z M i , + Z M j , + Z M k , + M b , = 0.

i=1            j=1

N          2

У Miz + У Miz + У Mllz + Mbz = o, iz               jzkzbz i=1            j=1

0 <  ц < 1,

F i ^ 0,

F i

< ц .

F.

i, max гДе Fi,max = KAi. i = 1. -. N •

В результате решения находятся мышечные усилия и реакции в суставах.

Необходимо отметить существующие различия между данной работой и работой [13]. В работе [13] была описана трехмерная модель жевательной системы человека, которая включала 18 неизвестных: 16 мышечных сил и 2 суставные реакции. Усилия связок не учитывались. Цель работы [13] заключалась в определении максимальной силы кусания и суставных реакций в данной точке кусания для различных положений этой точки. Усилия в мышцах в данной работе не определялись. Цель настоящей работы заключалась в определении мышечных сил и суставных реакций при априорно заданной силе кусания.

Рассмотрим пример, в котором происходит нагружение системы силой R , состоящей из трех мышц ОА , OB , OC , на концах которых находятся сухожилия, и трех связок OD , OE , OK (рис. 1).

Данная стержневая модель существует в организме человека в области голеностопа (рис. 2) [4]. Латеральная и медиальная головки икроножной, а также камбаловидная мышца вплетаются в ахиллово сухожилие, которое крепится к пяточной кости. Пяточная кость моделируется как точка О (см. рис. 1). От нее берут начало связки голеностопного сустава, которые перераспределяют усилие через ахиллово сухожилие другим костям сустава. Эти кости моделируются жесткой плитой, к которой приложена нагрузка R (см. рис. 1).

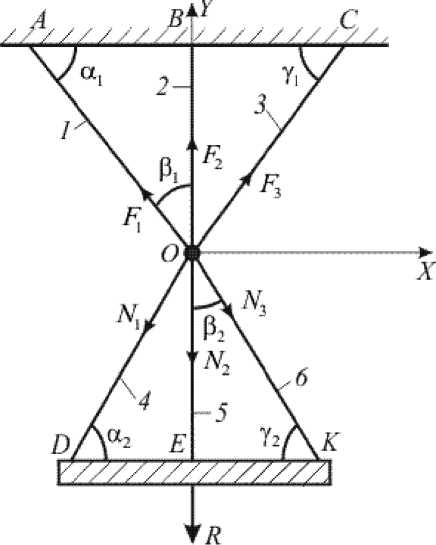
Рис. 1. Система стержней в общем виде: 1 – 3 – три стержня, моделирующие мышцы с сухожилиями на концах; 4 – 6 – связки, соединяющие точку О (кость) с другими костями

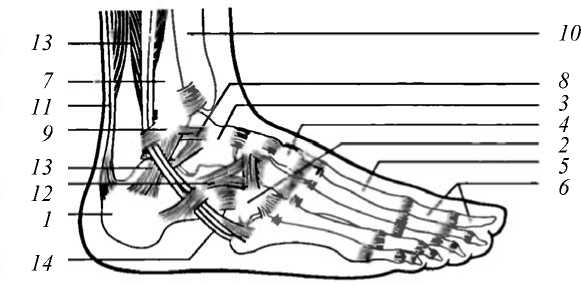
Рис. 2. Голеностопный сустав: 1 – пяточная кость; 2 – кубовидная кость; 3 – головка таранной кости; 4 – ладьевидная кость; 5 – первая плюсневая кость; 6 – кости большого пальца; 7 – малоберцовая кость; 8 – боковые связки голеностопного сустава; 9 – наружная лодыжка; 10 – большеберцовая кость; 11 – ахиллово сухожилие; 12 – раздвоенная связка; 13 – мышцы малоберцовой кости;

14 – сухожилие длинной малоберцовой мышцы [4]

Рассмотрим нижнюю часть системы стержней (рис. 3), отбросив верхнюю (см. рис. 1). В стержнях 4 – 6 появляются усилия N 1 , N 2 , N 3 . Данная система из трех стержней моделирует связки, линии действия усилий в которых сходятся в одной точке, т.е. система сил становится сходящейся. Для плоской системы сходящихся сил число уравнений равновесия уменьшается с трех до двух:

X : N 1 cos a 2 - N 3 cos у 2 = 0,

N 1 sin a ₂ + N 2 + N 3 sin у 2 - R = 0 .

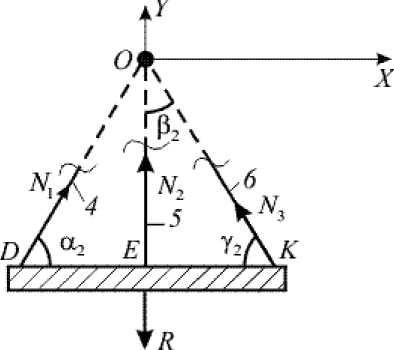
Рис. 3. Система стержней, моделирующая связки ( 4 – 6 ) на рис. 1

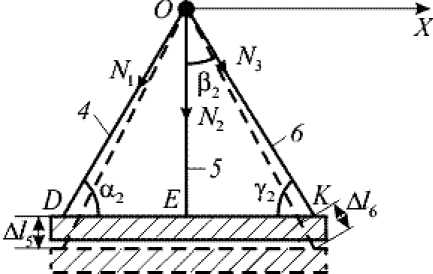
Рис. 4. Деформированная система стержней, моделирующая связки ( 4 – 6 )

Данная система уравнений (10)–(11) является статически неопределимой, поэтому необходимо добавить еще одно соотношение, которое позволит ее решить.

Для связок статически неопределимую задачу можно решить методом совместности деформаций, так как они являются пассивными элементами и не имеют сократительных элементов как мышцы, сокращающиеся под действием нервного возбуждения. Для этого запишем уравнение (12) с учетом малости деформаций (рис. 4)

A l 4 = A l 5 cos p ₂.                                   (12)

Возьмем стержни с одинаковой площадью поперечного сечения А = 3 см² из одного материала с модулем упругости Е и с пределом прочности [ с ] = 1600 H/см².

Углы а ₂ = в ₂ = у ₂ = 45 ° . Длины четвертого и шестого стержней l ₄ = l 6 = 1 м, а длина пятого стержня l ₅ = 0,707 м.

Зададим нагружающую силу R = 1000 H.

При учете определения деформации и закона Гука уравнение (12) приобретет следующий вид:

-"ЕаА ⁼ ~ЕА ^C0S ^ 2 или N ¹ 1 4 = N ² 1 5 cos в₂ •                     (13)

Система уравнений (10), (11) и (13) приобретет следующий вид:

N 1 cos 45 ° - N ₂ cos 45 ° = 0,

< N 1 sin45 ° + N ₂ + N ₃sin45 °- 1000 = 0,                    (14)

N 1 = 0,707 N ₂cos45 ° .

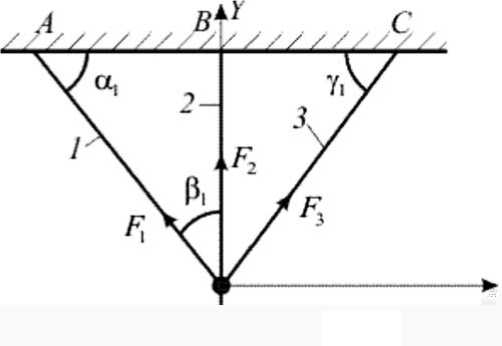
Рис. 5. Система стержней, моделирующая мышцы с сухожилиями ( 1 – 3 )

Решая данную систему, получим N 1 = N 3 = 235,5 Н и N ₂ = 668 H.

Рассмотрим верхнюю часть системы стержней (рис. 5), отбросив нижнюю (см. рис. 1). В стержнях 1 – 3 появляются усилия F 1 , F 2 , F 3 вследствие действия силы R 1 = R . Данная система из трех стержней моделирует мышцы с сухожилиями. В мышцах линии действия усилий сходятся в одной точке, т.е. система сил становится сходящейся. Для плоской системы сходящихся сил число уравнений равновесия уменьшается с трех до двух:

X : F 1 cos а 1 - F ₃ cos Y 1 = 0,

Y : F 1 sin а 1 + F 2 + F ₃ sin Y 1 - R 1 = 0 .

Рассмотрим несколько критериев оптимизации, позволяющих раскрыть статическую неопределимость для мышц [1].

Рассмотрим первый критерий оптимизации, который заключается в том, что сумма квадратов усилий мышц стремится к минимуму. Тогда получим систему уравнений

У F ² ^ min ,

V           F i , ‘ = 1,2,3

X : - F ₁cos a 1 + F 3 cos y ₃ = 0,                         (17)

• * Y : F 1 sin a 1 + F 2 + F ₃ sin Y 1 - R 1 = 0,

F i > 0, i = 1, 2, 3,

R 1 = 1000 Н.

Возьмем площадь поперечного сечения А , модуль упругости Е и предел прочности [ о ] такими же, как для связок. Углы a 1 = Y 1 = 30 ° , (3 1 = 60 ° . Длины первого и третьего стержней 1 1 = l ₃ = 1 м, а длина второго стержня l ₂ = 0,5 м.

Решая данную задачу, получаем, что F 1 = F 2 = 333,3 H, F ₃ = 666,7 H.

Рассмотрим второй критерий, который заключается в том, что сумма квадратов отношений усилий мышц к их максимуму, который они способны развить, стремится к минимуму ^

i

F i

F i ni a

^ min.

Запишем систему уравнений для данного критерия:

Е

i

F i F

V

^ min ,

F , i = 1,2,3

X : - F cos a , + F ₃ cos y 1 = 0,

F sin a , + F2 + F ₃ sin y 1 - R 1 = 0,

F >  0, г = 1, 2, 3,

R 1 = 1000 Н.

Решая данную задачу, получаем, что F 1 = F 2 = 333,3 H, F 3 = 666,7 Н. Данное решение совпадает с предыдущим, так как принято, что все мышцы способны развить одинаковые максимальные усилия.

Рассмотрим третий критерий, который заключается в том, что максимальное значение отношений усилий мышц к их максимуму, который они способны развить, стремится к минимуму (4). Тогда имеем задачу линейного программирования (8)–(9) при ограничениях

<

X : - F 1 cos a 1 + F ₃ cos у 1 = 0,

Y : F 1 sin a 1 + F 2 + F ₃ sin y 1 - R 1 = 0,

F > 0, г = 1, 2, 3,

R 1 = 1000 Н,

где F i max = kA i , i = 1,3; k - удельная мышечная сила, k = 37 Н/см²; A i - физиологическое поперечное сечение i -й мышцы.

Решая данную задачу, получаем, что F₁ = F 2 = F 3 = 500 Н.

Для решения первых двух задач применялся метод квадратичного программирования, использующий метод множителей Лагранжа для учета ограничений. Третья задача решалась симплекс-методом. Все решения были получены в пакете программ Mathematica 8 .

Выводы

Для всех критериев в ходе решения были получены близкие результаты значений усилий мышц. Для дальнейшего использования полученных результатов хочется остановиться на одном из критериев. Наиболее удачным и понятным с физиологической точки зрения является третий критерий, так как он подразумевает, что усилия в мышцах перераспределяются таким образом, чтобы они были равнонапряжены по отношению к максимальным усилиям в них. Организм пытается избежать случая, когда одна или несколько мышц будут сильно напряжены и усилия в них будут приближаться к максимальным значениям. Когда усилия приближаются к максимальным, мышцы быстро утомляются и могут порваться, растянуться; появятся болевые ощущения в этих областях. В работе [3] была подтверждена применимость данного критерия для нахождения мышечных усилий и реакций в височно-нижнечелюстном суставе.