Биомеханический анализ периодонтальной связки. Часть 2

Анализ структуры и свойств периодонтальной связки, например, в соответствии с [1–3], показывает, что для описания периодонтальной связки применима модель в виде тонкого слоя, адгезионно связанного с поверхностью зуба и альвеолярной костью. Учет пористости соединительной ткани и ориентированных волокон коллагена, обусловливающих неоднородность и анизотропию связки, позволяют, во-первых, получить ее более адекватное описание, во-вторых, обоснованно выбрать рецептуры и структурные схемы материала искусственного периодонта. Ниже рассматривается расчет перемещений корня зуба и напряженно-деформированного состояния периодонтальной связки с учетом неоднородности и анизотропии указанной биоткани.

Формулировка задачи

Рассмотрим волоконно-армированный пористый композит в виде тонкого слоя, адгезионно связанного с поверхностью зуба и альвеолярной костью. В предположении, что модуль упругости коллагеновых волокон значительно превосходит модуль упругости пористой матрицы и волокна направлены нормально к поверхности корня зуба, деформационные свойства данного однонаправленного композита можно охарактеризовать с помощью пяти независимых параметров – компонент тензора

модулей упругости Xmn (n, m = 1..6). Эти параметры определяются упругими константами Ламе и объемной долей содержания материала волокон Xf, цf, c, а также упругими характеристиками и пористостью материала матрицы Xf, цf , P, соответственно.

Используя статистический метод моментных функций [4], независимые компоненты тензора модулей упругости исследуемого материала можно определить следующим образом

,  _ , _п         ^{c (1 — c )( X}f ^{— X} 1 ^{)( X}f + ^цf ^{— X} i ^{— ц} 1 )

X13 = cX f +(1 — c )X1     77------7—7.---777-------7------, c (X1 + Ц1) + (1 — c )(Xf + ц f) + m

2 ^{( X} 11 ^{+ X} 12 ) = c ^{( X} f ^{+ Ц} f ) ^{+ (1 —} c ^{)( X} 1 ^{+ Ц} 1 )

^{c (1 — c )( X} f ^{+ ц} f ^{— X} 1 ^{— ц} 1 ^{) 2}

c ( X + ц 1 ) + (1 — c )( X f + ц f ) + m

X33 = c (Xf + 2 ц f ) + (1 — c )(X1 + 2Ц1) — c (1 — c )(Xf — X1)2

.            _л .      ^{c (1 — c )(} ц f ^— ц 1 ^{) 2}

X44 = cц f + (1 — c )ц1         7.----7

cц ₁ + (1 — c )ц f + m

c ^{(1 — c )(} ц f ^— ц 1 ⁾⁽ / + ^{3 m} )

X66 = cц f + (1 — c )ц.

^x             ( cц ₁ + (1 — c ) ц f )( l + 3 m ) + m ( l + m )

Здесь

,        (3 Xf + 2 ц f )(3X1 + 2 ц1)2

l = —г

3[c (3X1 + 2 ц1) + (1 — c )(3Xf + 2 ц f )]

ц1 ц f m =--------------, cЦ1 + (1 — c) ц f

№= Ц m (1 — P )² 1 — P

V

^3X m  ^{2 ц} ш

9 X m + 14 ц_т )

\ —1

,

X 1 = 2 X m

V

³ P ^{( X} m ^{+ 2 ц} т ^{)(3 X} m ^{2 ц} т ) ) (1 — p )² Г 2 — pl^ m 2 ^ m ) 9X m + 14 Ц m — P (3 X m — 2 Ц m ) /              2 Ц m J

Постоянные Ламе связаны с модулем упругости E и коэффициентом Пуассона ν известными соотношениями

(3 X + 2 ц ) ц        X

E = -------—, v =------- .

X + ц       2(X + ц )

Метод решения

Зная упругие характеристики материала периодонтальной связки, можно определить смещения зуба при силовом воздействии. Для этого необходимо решить задачу о равновесии зуба под действием внешних усилий Fi (i = 1..n) и адгезионных напряжений p(rS), возникающих на поверхности раздела «связка - корень зуба». Здесь rS - радиус-вектор рассматриваемой точки на поверхности корня зуба. Адгезионные напряжения зависят от смещений точек rS. Смещение любой точки твердого тела можно выразить через 6 независимых величин: смещение й некоторой точки O и углы поворота относительно осей координат ϕi . В случае малых углов поворота смещения можно представить следующим образом ux = uxO + zVy - yVz , uy = uyO + xVz - zVx , uz = uzO + y^x - x^y •

Тогда уравнения равновесия зуба можно записать в виде nn 7-

7/7  7   7\ JC1 , X Т7    А    I 1 7■    7V7■  7   7\     , X 7 Т7    А/

P(rS, uO, ф)dS + L Fi= 0,  JJ rS x P(rS’ uO, Ф) dS + L riX Fi= 0(4)

S                           i=1               Si

Здесь r i - радиус-вектор точки приложения силы F i . Интегрирование ведется по площади контакта корня зуба с периодонтальной связкой. Решение системы уравнений (4) позволяет определить u O , ф и, следовательно, смещения всех точек зуба. Реализация изложенной методики затрудняется тем, что для определения перемещений необходимо знать функцию влияния для ортотропного слоя сложной конфигурации, адгезионно связанным с жестким основанием. Определение указанной функции представляет значительные трудности даже в двумерной постановке [5, 6].

Можно показать, что решение задачи можно существенно упростить, если принять во внимание характерные размеры и условия нагружения периодонтальной связки.

Известно, что для тонких покрытий справедлива гипотеза Винклера [7]. Если характерные размеры области контакта L значительно превосходят толщину покрытия, последнее можно представить как совокупность несвязанных упругих элементов, и контактное давление определяется простым выражением

-/-    _1(г             г- p(rS ) = Дknun (rS ) + kTuT (rS ))•                               (5)

h

Здесь un, йт - нормальное и тангенциальное смещение точки поверхности покрытия; h - толщина покрытия; kn, kT - нормальная и тангенциальная жесткость покрытия, соответственно.

Правомерность гипотезы (5) для тонких ортотропных покрытий (в двумерной постановке) показана в работе [6], где соотношения давлений и перемещений выведены из общего решения контактной задачи для ортотропной полосы при L >>h . В [5] также показано, что для полосы, адгезионно связанной с жестким основанием, нормальная жесткость совпадает с компонентой Х ₃₃ = X_zz тензора модулей упругости

(ось z направлена нормально основанию), а тангенциальная - с модулем сдвига Gxz. Таким образом kn = Х33, кт = ^44.                                      (6)

Для подтверждения корректности данного подхода в трехмерной постановке рассмотрим равновесие квадратной пластины с длиной стороны L на ортотропном слое толщиной h (рис. 1).

Упругие характеристики материала слоя выбраны следующими:

E = E = 5 МПа ;           E_z = 50 МПа;           v_xv = 0,25;           v_xz = v_vz = 0,1;

x y                                z                                xy                           xz yz

Gxy = Ex/2(1 + vxy) = 2 МПа ; Gxz = Gyz = 10 МПа . Нормальная и тангенциальная жесткость слоя выражаются следующим образом

k

n

E z ²(1 - V xy )

E z ^{(1 - V} xy ) ^{- 2} E x ^V xz²

, к т = G xz •

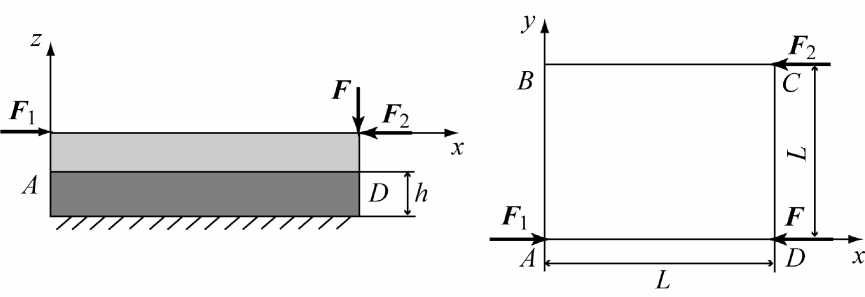
Рис. 1. Схема нагружения ортотропного слоя: а – вид сбоку, б – вид сверху

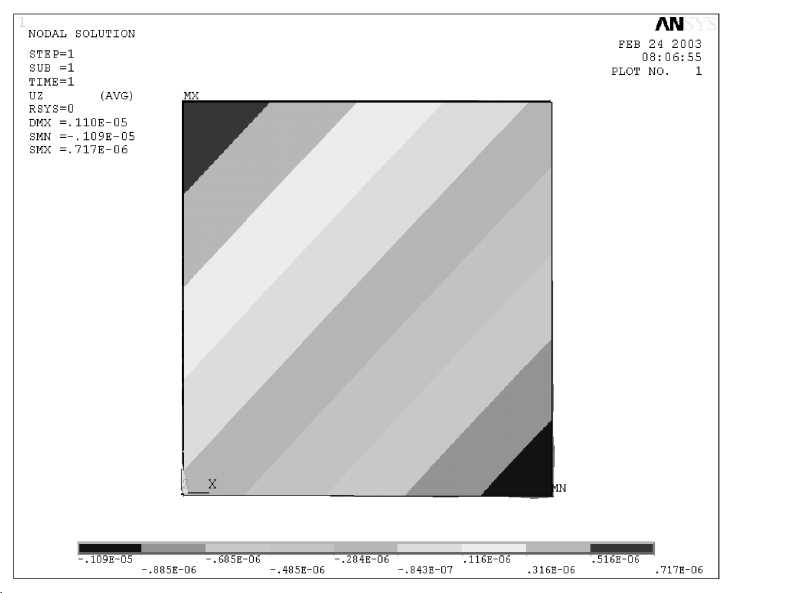
Рис. 2. Распределение осадки u_z точек жесткой пластины

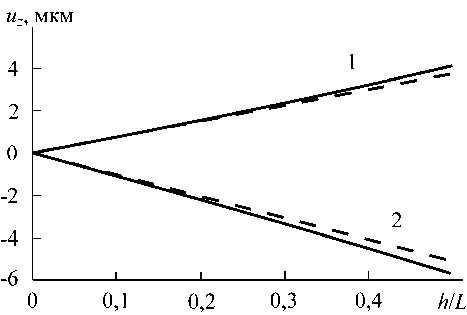
Рис. 3. Зависимость смещения точек B (кривая 1) и D (кривая 2) от отношения толщины покрытия h к длине стороны L

На рис. 2 представлено распределение смещений u_z точек пластины под действием сжимающего усилия F z =- 100 Н, приложенного к точке A (рис. 1), найденное численным методом конечных элементов (МКЭ). Используя соотношения (3-5), для смещений точек D и B получим

Рис. 4. Распределение перемещения u_x точек жесткой пластины

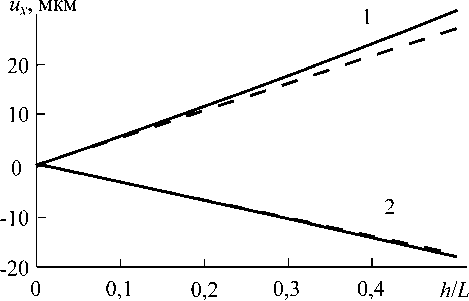
Рис. 5. Зависимость смещения точек A (кривая 1) и C (кривая 2) от отношения толщины покрытия h к длине стороны L

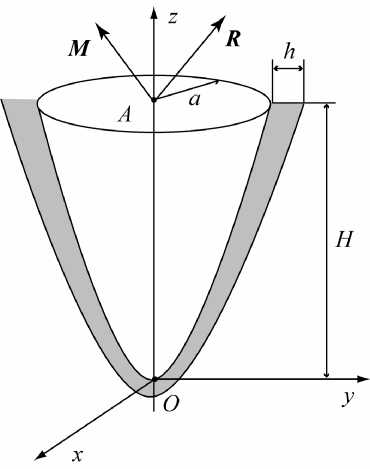
Рис. 6. Модель связочного соединения корня зуба с альвеолярной костью uB

5 Fh        7 Fh

k . L 2 ’ u D =

—

k n L ^{2 .}

Результаты использования полученных выражений, показанные пунктиром на рис. 3, сопоставлены с результатами расчета численным методом конечных элементов (сплошные линии).

Далее рассмотрим нагружение пластины силами F 1x = 200 Н и F 2x = 100 Н

(рис. 1). В соответствии с гипотезой (5) для смещений точек A и C запишем uA,C = u0 ± L (1 + sin Ф — cos Ф), где u 0 =

F 1

—

F 2

г

k_τL ²

h , ф = arcsin

V

6( F i + F 2 ) k_τL ³

)

h

)

Поле перемещений точек пластины, найденное методом конечных элементов, показано на рис. 4. На рис. 5 сопоставлены смещения точек A и C , определенные МКЭ (сплошные линии) и с использованием гипотезы Винклера (пунктирные линии). Анализ графиков на рис. 3 и 5 позволяет заключить, что при h <  0,2 L гипотеза Винклера (5)

дает возможность достаточно точно прогнозировать перемещения точек твердого тела на ортотропном слоистом основании.

Известно [2], что длина полуосей эллипсов верхнего поперечного сечения корня зуба более чем на порядок величины превышает толщину периодонтальной связки. Следовательно, гипотеза (5) может использоваться для описания смещений корня зуба при силовых воздействиях, и соотношения (3), (4) и (5) позволяют определить смещения корня зуба под действием внешних нагрузок. Коэффициенты жесткости k n и к _т определяются по формулам (1), (2) и (6).

Пример расчета

Используем изложенное решение для анализа равновесия тела, близкого по форме корню зуба. В качестве примера рассмотрим конус высотой H и радиусом верхнего поперечного сечения a (рис. 6). Поверхность контакта конуса с трансверсально-изотропной связкой толщиной h описывается следующим образом

z ( x , У ) = — V x ² + У ² .                               (8)

a

Зная форму поверхности контакта, можно определить нормальное и тангенциальное смещения точек поверхности un, uT. Подставляя un, uT в равенства (5) и (4), уравнения равновесия можно записать в виде uxo   , na , [(kn — k-)H2 + 2k, (a2 + —2)]+Ф, 1 naHia2 + H2 (k„ + k,) = Rx,

2V a ² + H ^{2                                 3}

u yo    , П^а у [ ( k n — k , ) H ² + 2 k , ( a ² + H ²) ] — ф x ¹ naHyla ² + H ² ( k „ + k , ) = R , ,

2V a ² + H ^{2                                3}

u zo -₁=n^a= ( k n a ² + k T H ²) = R z ,

V a ² + H²

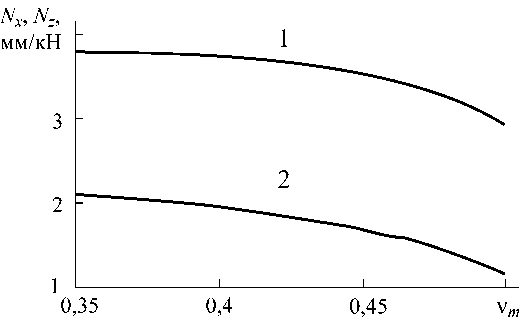
Рис. 7. Зависимость продольной (кривая 1) и поперечной (кривая 2) податливости периодонтальной связки от коэффициента Пуассона твердой фазы v _m при пористости P =0,1

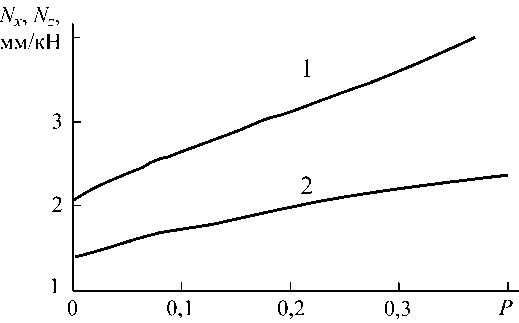
Рис. 8. Зависимость продольной (кривая 1) и поперечной (кривая 2) податливости периодонтальной связки от пористости P при v_m = 0,475

- u yO 1 naHa ² + H ² ( k n + k_T ) +ф_х 1 nA a ² + H ² [ k n ( a ² + H ²) + k_T H ² ] = M x - HR y , u_xO 1 naHa ² + H ² ( k n + k_T ) +ф_у 1 naA ² + H ² [ k n ( a ² + H ²) + k_TH ² ] = M y + HR x ,

ф_z k_Tna ³ V a ² + H ² = M_z •

Здесь R , M - главный вектор и главный момент внешних сил, приведенные к точке A (рис. 6). Если известны свойства компонент связки X f , ц f , c , X f , ц f и P , выражения (1), (2) и (6) позволяют определить величины k_n и k_τ . Для определения перемещений следует решить систему (9).

В качестве примера рассмотрим нагружение конуса ( a = 0,3 см , H = 1 см ) силой

——

——

R , приложенной в точке A и лежащей в плоскости xz (M = 0, R y = 0). Введем две дополнительные величины

N = u xA- , N = u zA ^x   R x      ^z R z

•

Величину N_x назовем поперечной, а N_z - продольной податливостью зуба. Податливости определяются формой корня зуба a , H , а также упругими характеристиками и пористостью композитной связки X f- , ц f , c , X f , ц f , P •

На рис. 7 и 8 представлены зависимости податливости связки от коэффициента Пуассона и пористости твердой фазы при E f = 10 МПа, E m = 1 МПа, Vf = 0,35 и c = 0,2 • При указанных параметрах продольная податливость более чем в 2 раза превышает поперечную. Если материал твердой фазы матрицы является несжимаемым

( v_m >  0,45), податливость связки заметно уменьшается с ростом v_m . Увеличение пористости матрицы приводит к увеличению податливости, причем скорость изменения продольной податливости с ростом P значительно превосходит скорость изменения поперечной податливости.

Заключение

Использование гипотезы Винклера позволяет упростить биомеханический анализ периодонтальной связки в виде пористого ортотропного слоя, адгезионно связанного с корнем зуба и альвеолярной костью. Полученные соотношения могут быть использованы для определения смещений зуба под действием жевательной или корректирующей нагрузки, а также при идентификации упругих характеристик армирующей и матричной компонент периодонтальной связки.

Благодарности

Работа выполнена при поддержке фонда БРФФИ–РФФИ (проект Т02Р–014).