Биомеханическое моделирование эффекта сближения фрагментов твердого неба при ортопедическом лечении

Врожденная расщелина верхней челюсти («волчья пасть», uranoschisis, labium leporium ) является наиболее часто встречающимся и серьезным заболеванием зубочелюстной системы. Оно нарушает анатомическое соотношение всех тканевых структур среднего отдела лица, изменяет физиологическое равновесие мышц приротовой полости, поражает жизненно важные функции, такие как сосание, глотание, дыхание, речь, а также производит выраженный косметический эффект. По данным Всемирной организации здравоохранения, в мире частота рождения детей с данной патологией составляет в среднем 0,5–1,5 на 1000 новорожденных. Ввиду ухудшения экологии наблюдается тенденция к увеличению количества детей с этим заболеванием [1].

Важную роль в устранении расщелины играет раннее ортопедическое лечение. Оно нацелено на сближение разобщенных фрагментов твердого неба без хирургического вмешательства. Чем успешнее будет проведено ортопедическое лечение, тем ближе будут низведены фрагменты и тем безопаснее будет проведение операции по их сшиванию. Поэтому использование биомеханического анализа позволит лучше понять процессы, происходящие при лечении, и предложить новые более эффективные ортопедические устройства.

Один из методов ортопедической коррекции разработан в Республиканском научно-практическом центре медико-социальной реабилитации детей и подростков с врожденной челюстно-лицевой патологией «Бонум» (г. Екатеринбург) и применяется с 1989 г.

Няшин Юрий Иванович, д.т.н., профессор, завкафедрой теоретической механики, Пермь

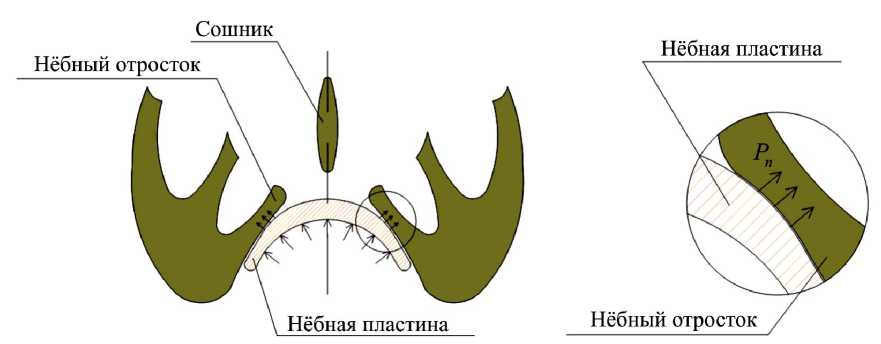
Рис. 1. Схема устройства нёбной пластины

Данный подход к лечению этой категории больных заключается в разработке метода ранней предоперационной реконструктивно-коррекционной терапии, для проведения которой используется индивидуально изготавливаемая ортопедическая аппаратура (ортопедическая пластина), создающая оптимальные условия для процессов роста и развития фрагментированных отделов верхней челюсти [11, 12].

Схема установки аппарата приведена на рис. 1.

Контактное давление P_n , возникающее между пластиной и фрагментом нёба, создается языком (на рисунке не показан), поскольку при кормлении он рефлекторно прижимается к нёбу. В результате формируется физиологический для данного пациента свод нёба, расщелина уменьшается, что приближает сроки проведения операции уранопластики [11].

С точки зрения механики, эффект сближения недоразвитых фрагментов твердого нёба кажется неясным: действие языка приводит, на первый взгляд, к изгибающему моменту во фрагментах, что, казалось бы, должно вызвать дальнейшее расхождение фрагментов. В данной статье приводится объяснение эффекта сближения, т.е. объяснение механизма управления ростом нёбных фрагментов на основании гипотезы о ростовых деформациях.

Биомеханическая модель роста

Одной из первых работ, посвященных моделированию роста с позиций биомеханики, была работа [10]. После этого более детально вопросы роста изучены в исследованиях [2–4, 6, 9, 14]. В работах [3, 9] предложена модель растущего тела как трехфазной среды, содержащей твердый матрикс, внутриклеточную жидкость и межклеточную жидкость (интерстиций). Рост происходит за счет массообмена между твердой фазой и внутриклеточной жидкостью. К сожалению, в данное время использование такой модели затруднительно, так как многие параметры, описывающие процессы транспорта и массопередачи, не определены.

Деформации роста, вообще говоря, конечны, особенно если речь идет о процессах роста целых органов (например, рост сердца цыпленка [14]), и необходимо рассматривать деформации скорости для полной, упругой и ростовой деформаций соответственно:

5=5 ^е +5 g . (1)

Однако для моделирования сближения фрагментов твердого нёба достаточно рассмотреть малые деформации, тогда тензор | e может быть вычислен через закон

Гука следующим образом:

Ie = d ( C-1 --G) , dt

где C ¹ - тензор упругой податливости.

По данным исследований, ростовые процессы существенно зависят от напряжений, действующих в ткани, и одним из простых вариантов модели для деформации скорости роста является модель Хсю [10]:

I g = А + В .-G ,                                    (3)

X

где А , В – тензоры, определяющие рост живой ткани.

X

Построение тензоров А и В требует глубокого теоретического и экспериментального исследования. Если принять гипотезу об изотропии материала и роста, то в этом случае тензоры должны быть изотропными, и компоненты тензоров не должны зависеть от поворота или отражения координатных осей, что позволит упростить соотношение (3).

Известно [5], что среди тензоров второго ранга существует только один линейно-независимый изотропный тензор

Aj = AS j , где 5j - символ Кронекера.

Среди тензоров четвертого ранга можно выделить три линейно-независимых изотропных тензора [5]

-5. 5Н,      = 5,5 , ±5,5 ,,                        (5)

ijkl ij kl ,        ijkl ik jl il jk , поэтому запишем тензор В в следующем виде:

В»I = X 5„5„ + Ц (5»5, + 5,5,) + ц (5а5, - 5,5,).                  (6)

ijkl           ij kl             ik jl il jk         1 ik jl il jk

Вычислим двойную свертку тензора (6) и тензора напряжений:

X

(В • -G)j = BjklGkl = X 5 jGkk + ц (G j + Gj ) + Ц1 (G j - Gji) ,

BijklGkl = ^5jGkk + 2цО/у , предполагая симметрию тензора напряжений и вводя обозначение gkk = G11 + g22 + G33 = 11 (су) - первый инвариант тензора напряжений.

В результате деформация скорости роста принимает вид

1 g = A5 j+^5 jG kk+ 2ЦС j.

В работе [11] сделана упрощающая гипотеза (коэффициент X положен равным нулю) и соотношение (8) записано в виде

I g = AI + B с .

Эта гипотеза позволила определить константы A и B экспериментально.

К вопросу об управлении ростовыми деформациями

Соотношение (9) показывает, как действующие напряжения могут повлиять на рост: растягивающие напряжения стимулируют рост, а сжимающие – замедляют (при B >  0 ).

Таким образом, задача о лечении врожденной расщелины твердого нёба может быть рассмотрена как задача об управлении ростом, т.е. задача о создании в теле заданной ростовой деформации. Подход к решению таких задач разработан в работах [7, 8, 13] и основан на теореме о декомпозиции собственной деформации на составляющую, свободную от напряжений, и составляющую, свободную от деформаций [13]. Кроме этого, разработан алгоритм независимого управления собственными деформациями, т.е. алгоритм управления, при котором ростовая деформация не будет вызывать макроскопических напряжений.

Под собственной деформацией понимается неупругая деформация любой природы, т.е. деформация 8 является суммой упругой 8 e и собственной 8 * деформаций:

8 = 8 e +8 * .                                       (10)

Предполагается, что собственные деформации 8 * можно найти отдельно, используя соответствующие определяющие соотношения. Например, для температурной деформации такое соотношение имеет вид 8 * = аA T ( а - тензор коэффициентов температурного расширения, A T - изменение температуры, отсчитываемое от состояния, в котором д = 0, 8 = 0, и = 0), для ростовой деформации необходимо использовать соотношение (9).

Применительно к данной задаче разработанный подход позволит найти давление P_n , действующее на фрагмент твердого нёба (рис. 1) и вызывающее рост живой ткани в заданном направлении. Этого можно достичь, решив следующую задачу:

Ф ( P , Н( 8 ⁰ -8 ( P , ) ) • < .. ( 8 ⁰ -8 ( P , ) ) dV ^ inf ( P , ) ,             (11)

V где 80 - деформация, обеспечивающая заданное сближение фрагментов, 8* (Pn) -ростовая деформация, вызванная давлением Pn .

Отметим, что после снятия ортопедической пластины в небных фрагментах останутся накопленные ростовые деформации. Важно, чтобы они не создавали остаточных напряжений и, как следствие, не вызывали других нежелательных процессов. Поэтому поиск решения задачи (11) ведется в классе собственных деформаций, свободных от напряжений, что позволит сохранить напряжения в растущих фрагментах.

Постановка задачи

В качестве примера рассмотрим собственно эффект сближения фрагментов за счет накопления ростовой деформации при действии давления со стороны ортопедической пластины.

Полная дифференциальная постановка задачи растущего упругого тела, занимающего область V в R³ с границей S , V = V и S , S = S v и S _д и S_p (угловая точка (0; 0) не входит в границы S v и S _о ), должна включать в себя:

определяющие соотношения (1–3);

уравнения равновесия

V-д = 0, V r е V , t >  0 ,                              (12)

ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 1 (55): 38–45                       41

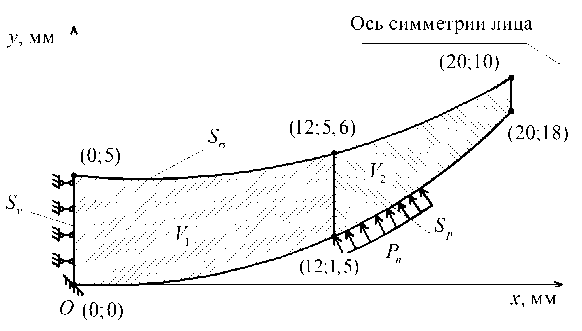
Рис. 2. Плоская модель небного отростка кинематические соотношения

| = 1 (VV + VV), Vr e V, t > 0,(13)

граничные условия

Vx = 0, тxy = 0, Vr e Sv, t > 0,(14)

V = 0 (x = y = 0), t > 0,(15)

V n-5 = 0, VV e S,, n-5 = Pn, Vr e Sp, t > 0,(16)

начальные условия

U = 0, t = 0, Vr e V .(17)

Однако для объяснения эффекта сближения фрагментов достаточно рассмотреть более простую задачу о вычислении напряжений в момент приложения ортопедической нагрузки P_n ( t = 0, в этот момент ростовые деформации равны нулю):

^*

7-5 = 0, VV e V, ст = C--к, Vr e V, s = 1 (VU + uV), Vr e V,                                    (18)

*

n -5 = 0, V r e S^ , n -5 = P_n , V V e S_p , 5                  n               p

V

U x = 0, T xy = 0, V r e S v , u = 0 ( x = y = 0).

Затем можно вычислить деформации скорости | g в формуле (9). Этот анализ позволит выявить зоны «ускоренного» и «замедленного» роста и объяснить эффект сближения фрагментов.

Геометрические параметры области находятся в физиологическом диапазоне, их величину можно оценить по координатам точек, которые приведены на рис. 2.

Свойства материала ткани ( E = 10⁴ МПа, ц = 0,3 ) фрагмента взяты из работы [11]. Известно, что фрагмент твердого нёба состоит из двух частей: податливой хрящевой ткани (область V ₂ ), соединенной с более жесткой костной структурой (область V ₁ ) [12].

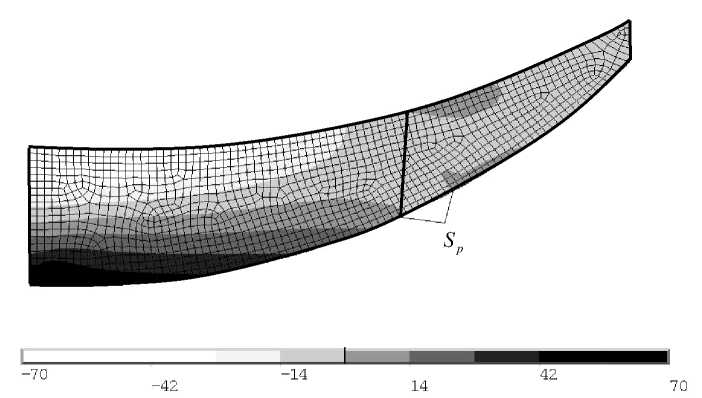
Рис. 3. Распределение напряжений о x (г / мм2) в расчетной области

Поэтому в определяющем соотношении для ростовой деформации в области V ₁ ,

~ ,_ ~ которое применяется в виде формулы ^ g = А + В --о , V r е V 1 , компонентами тензора В пренебрегаем. В области V ₂ , где напряжения вызывают заметную реакцию ткани, параметры ростовой деформации имеют следующие значения: А = 0,0025 (1/мес) , В = 0,002 (мм²/(г - мес)) [11].

Наличие ортопедической пластины моделируем граничными условиями (16). Давление, создаваемое ортопедической пластиной, мало и может повлиять лишь на податливую структуру, поэтому в расчете нагрузку P_n прикладываем только к области V 2 . Величина P n = 10 г /мм² выбрана исходя из условия невозникновения травм слизистой оболочки и костной ткани твердого неба. Длина границы S_p (длина области контакта) взята из работы [11].

Анализ решения

Скорость ростовой деформации, приводящей к сближению отростков, примет вид

^ = А + В о_п.                             (19)

Для объяснения эффекта сближения рассмотрим скорости ростовых деформаций (19), возникающих в области, представленной на рис. 2, от действия ортопедической пластины. В конечно-элементном пакете ANSYS разобьем указанную область плоскими элементами, средняя длина ребра которых равна 0,25 мм. Найдем распределение напряжений о x в области V , при нагружении ее границы S_p давлением P n = 10 г /мм² . Распределение напряжений о x приведено на рис. 3. Область приложения нагрузки (начало и конец границы S_p ) также показана на рисунке.

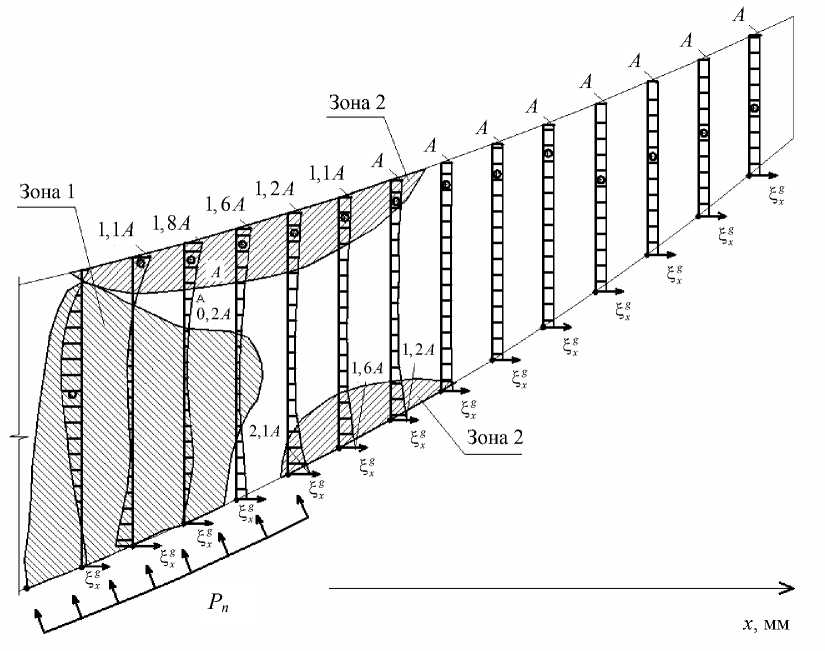
Обозначим вдоль нижней границы области V ₂ точки 1, 2… n с шагом 1 мм. Проведем из каждой указанной точки прямую к верхней границе области. На рис. 4 приведены эпюры скоростей ростовых деформаций ^ g фрагмента вдоль указанных линий для области V ₂ .

Для оценки полученных результатов обозначим на фрагменте «зоны роста»: «зону 1» , где ^ g <  0,2 A = 0,0005 (1 / мес) , и «зону 2», где ^ g >  A = 0,0025 (1 / мес) .

ISSN 1812-5123. Российский журнал биомеханики. 2012. Т. 16, № 1 (55): 38–45                       43

A

A

A

0,2 A

1,2 A

1,6 A

2,1A g x g x g x g x

g

x

g

x

g

x

A g x g x g x g x

A

g

x

Зона 2

A

P n

Зона 2

Зона 1

1,1 A ^A

1,2 A ,

1,6 A ,

A

A g x g x x, мм

Рис. 4. Эпюры скоростей ростовых деформаций ξ _x ^g , (1/ мес) в области V ₂

Оценим полученные результаты. В области контакта под действием ортопедической пластины возникают сжимающие напряжения (см. рис. 3), которые подавляют рост «нижних» волокон материала – рост в направлении оси Ох в этой области замедляется («зона 1»). В областях, где возникают растягивающие напряжения, наблюдается ускоренный рост волокон – «зоны 2». В области контакта рост «верхних» волокон опережает рост «нижних». Вследствие этого возникает изгиб фрагмента в направлении роста, что объясняет феномен сближения фрагментов с позиций теории ростовых деформаций.

Отметим, что давление P_n и область контакта (граница S_p ) должны подбираться индивидуально для каждого пациента. Расчеты показывают, например, что при увеличении зоны действия нагрузки P_n фрагменты будут расходиться [11]. Ключевую роль в поиске оптимального давления должен играть биомеханический анализ пациента, основанный на гипсовых контрольно-диагностических моделях или магнитно-резонансной томографии. В результате анализа должны быть даны рекомендации по выбору нужной формы ортопедической пластины.

Заключение

В данной статье показано, что благоприятное поле напряжений может вызывать рост живой ткани в заданном направлении. С точки зрения механики, задача об ортопедическом лечении видится как задача управления ростовыми деформациями. Теоретические основы решения таких задач разработаны авторами [7, 8, 13] и могут эффективно применяться для разработки оптимальной методики ортопедического лечения врожденной расщелины твердого нёба. Применение математического моделирования и компьютерной симуляции позволит предсказать исход ортопедического лечения и провести «виртуальное лечение». Это важно как для лечащего врача, так и для психологической поддержки родителей ребенка.

Благодарности

Работа поддержана Российским фондом фундаментальных исследований (проект № 11-01-00910).