Биомеханическое моделирование трабекулярной костной ткани в состоянии равновесия

Рассмотрим стационарную задачу о плоской деформации образца из трабекулярной костной ткани как задачу линейной теории упругости анизотропного тела, дополненную кинетическими уравнениями, описывающими перестройку костной ткани. Математическая постановка задачи состоит из 21 скалярного уравнения [3]:

Пермь

Няшин Юрий Иванович, д.т.н., профессор кафедры теоретической механики и биомеханики, Пермь уравнения равновесия:

• V- 6 = 0, x e V, t > 0,(1)

определяющего и геометрического соотношений:

<6 = (gi + g2e) (tr ё)1Ё + (gз + g4e)£ + g5 (ie - K + K - £) + g6 (tr (K - e)1E + (tr e)K),

~   1 —-  -^

£ = — (V u + u V ) , эволюционного уравнения, описывающего изменение ориентации трабекул в рассматриваемой области:

К = (h + he)(£-£0) + h tr(e-£0)K +

+ h ^ ( tr( K - (£ - £⁰ )) ) E - 3 ( K - (£ - £⁰ ) + (£ - £⁰) - K ) ) , эволюционного уравнения, описывающего изменение плотности губчатой костной ткани в рассматриваемой области:

e = (fi + f2 e) (tr £ - tr £0) + f3 (tr(K - (£ - £0)) ), граничных условий:

n - 6 = P(t), x = S^, t > 0, u - U(t), x = Su, t > 0, начальных условий:

IK = K0, e = e0, x e V, t = 0,(6)

P = P0, x e SCT, U = U0, x e Su, t = 0, где f -f, h -h - константы [3, 4], сут”1; gY -g - константы [8, 9], ГПа; К - девиатор тензора структуры (отвечает за направление трабекул); e – изменение доли твердого объема (отвечает за пористость).

Интересно посмотреть на поведение трабекулярной костной ткани под нагрузкой в момент времени, когда ее структура находится в состоянии равновесия. Для примера кость моделируется как прямоугольная пластина, нагруженная с одного торца растягивающей нагрузкой, а с другого конца пластина жестко закреплена (рис. 1).

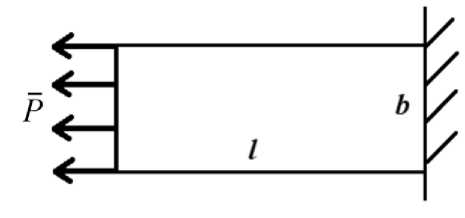
Рис. 1. Схематичное представление модели

В зависимости от того, какие данные заданы и какие нужно найти, можно выделить три типа задач:

• 1.    Даны K 0 , P ⁰, e ⁰, найти d⁰, E⁰ .

• 2.    Даны d⁰, E⁰ , найти K⁰, e⁰ .

• 3.    Даны K 0 = 0, i , j = i...3 (изотропия), d⁰, E⁰ , найти E , v .

Решение стационарных задач

Определение напряженно-деформированного состояния

Решение первой задачи является ответом на вопрос: какое напряженно-деформированное состояние реализуется в кости определенной микроструктуры под заданной нагрузкой?

Определяющее соотношение (2.1) представляет собой форму записи обобщенного

^

закона Гука су = C •• e , в котором тензор упругих констант является симметричным тензором четвертого ранга, зависящим от структуры материала следующим образом (используется нотация Фойгта):

C ii = ( g i + g 2 ^e) + ⁽ g 3 + g 4 ^e) + ² K _n ⁽ g 5 + g 6 ), C 12 = ⁽ g i + g 2 e ) + g ₆( K ii + K 22 ) , C = ( g i + g 2 e ) — g 6 K 22 , C 14 = K 23 g 6 , C 15 = K 13( g 5 + g б ), C i6 = K i2 ( g 5 + g 6 ),

^C 22 = ⁽ g i ⁺ g 2 e ) ^{+ (} g 3 ⁺ g 4 e ) ^{+ 2 K} 22 ⁽ g 5 ⁺ g 6 ), ^C 23 = ⁽ g i ⁺ g 2 e ) — g 6 ^K ii ,

^C 24 = ^K 23 ^{( g} 5 ^{+ g} 6 ), ^C 25 = ^K i3 ^g 6 , ^C 26 = ^K i2 ^{( g} 5 ^{+ g} 6 ),

^C33 = ⁽ g i ⁺ g 2 e ) ^{+ (} g 3 ⁺ g 4 e ) — ^{2( K} ii ^{+ K} 22⁾⁽ g 5 ⁺ g 6 ), ^C 34 = ^K 23 ⁽ g 5 ⁺ g 6 ) ,

^C 35 = ^K 23 ^{( g} 5 ^{+ g} 6 ), ^C 36 = ^K i2 ^g 6 , ^C 44 = 2 ^{(( g} 3 ^{+ g} 4 e ) - ^g 5 ^K ii ),

^C 44 = "2"^{(( g} 3 ^{+ g} 4 e ) ^{— g} 5 K ii ), ^C 45 = "2 ^K i2 ^g 5 , ^C 46 = 2 ^K i3 ^g 5 , ^C 46 = 2 ^K i3 ^g 5 , ^C 55 = 2^{(( g} 3 ^{+ g} 4 e ) - ^g 5 ^K 22 ), ^C 56 = "2 ^K 23 ^g 5 , ^C 66 = "2" ^{(( g} 3 ^{+ g} 4 e ) ^{+ g} 5^{( K} ii ^{+ K} 22 ^)).

В ANSYS уравнения (7) записываются в таблицу свойств материала командой TBDATA . Напряженно-деформированное состояние определяется в результате решения задачи методом конечных элементов с учетом внешних сил и ограничений на перемещения (рис. 2).

Для решения задачи в ANSYS используем конечный элемент Plane182 .

Аналитическое решение задачи требует индивидуального подхода к получению тензоров напряжений и деформации. Решение задачи на рис. 1 аналитическим методом можно получить, сделав следующие предположения.

Допустим,     что     реализуется     плоское     напряженное     состояние

( ^Gz ~ ^Txz ~ Tyz * 0; Yxz ~ Yjz ~ 0 ). Тогда благодаря принципу Сен-Венана можно заменить влияние заделки неким напряжением о_х , действующим на поперечное сечение A = b (см. рис 1). Из уравнения равновесия для оси x (о^ b - P = 0) находится g_x = P / b .

Так как касательные и нормальные напряжения, действующие на площадках, перпендикулярных оси у , отсутствуют, то о_у * 0, т_ху * 0.

/\ PRNSOL Command                                    X

File

NODE	SX	SY	SZ	SXY	SYZ	SXZ
7	0.10003E4J06	7.3651	0.0000	-2.4388	0.0000	0.0000
21	□ .100ОЗЕЧ106	7.3651	0.0000	2.4388	0.0000	0.0000
41	99996.	9.3095	0.0000	-3.3817	0.0000	0.0000
42	99983.	14.613	0.0000	0.16555E-007	0.0000	0.0000
43	99996.	9.3095	0.0000	3.3817	0.0000	0.0000

/\ PRNSOL Command                                     X

File

NODE	EPaX       EPELY       EPELZ       EPELXY	EPELVZ	EPELXZ	A
7	0.16108E-D03-0.27D29E-D04-0.27D43E-D04-0.91734E-D08	0.0000	0.0000
21	0.161D8E-D03-0.27D29E-004-0.27D43E-D04 0.91734E-DD8	0.0000	0.0000
41	D.161D3E-DD3-0.27D17E-D04-0.27035E-D04-0.1272DE-D07	0.0000	0.0000
42	0.16101E-003-0.27005E-D04-0.27033E-D04 0.16368E-015	0.0000	0.0000
43	0.16103E-003-0.27017E-004-0.27035E-004 0.12720E-007	0.0000	0.0000	V

Рис. 2. Компоненты тензора напряжений и деформации для сечения x ® l /2 в ANSYS

Оставшиеся 4 неизвестных ( ε , ε , ε , γ ) находятся из четырех уравнений закона

Гука

° x = C _n£ x + ^С 12^е y + C 13 & z , ° y = ^С 12^е x + ^C 22^е y + ^C 23^е z , 0 = C 13 ^ x + C 32 ^ y + C 33 ^ z ,

^T xy = ^C 66^е xy .

Тогда

ε _z

° x ( C 3 C 22 - C 13 C 2 C 23 )

3    2      22          ,

13  22 + ^ ^13  12  23   ^11  23  13   ^12  33  13 ⁺   11  33  13  22

С С

12  33

y

13  22

-

-

С СС

13  23

-------е , е —е zxy

C12C23

С

- —e_z, е = 0.

z     xy

C ₁₃

Тот же результат получается из четырех уравнений, записанных через матрицу податливости,

^е x   ° x ■ ^C 11   , ^е y ° y ■ ^C 21   ,   ° z ■ ^C 31   ,   ^T xy   0.

С учетом (1) и (2.1), а также зная, что компоненты тензора K равны нулю при P = 1 кН (°_х = 10 000 Па), получаются следующие значения:

е = 0,16104 - 10 ^{- 4}, е = е - 0,27034 - 10 - 5 , y = 0 . x             yz             xy

Аналитическое решение (11) совпадает с численным с точностью А = 10 ^{- 8}.

Связь компонент тензора малой формулами Коши:

деформации с перемещениями определяется

ди е = — е xx    дx ’ yy

д v        д а

—, е = — xx дy       дz

.

д

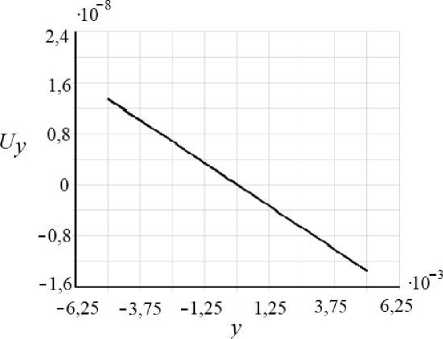
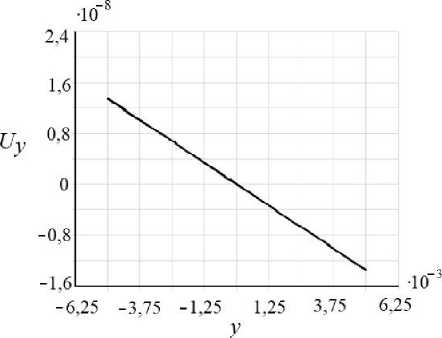
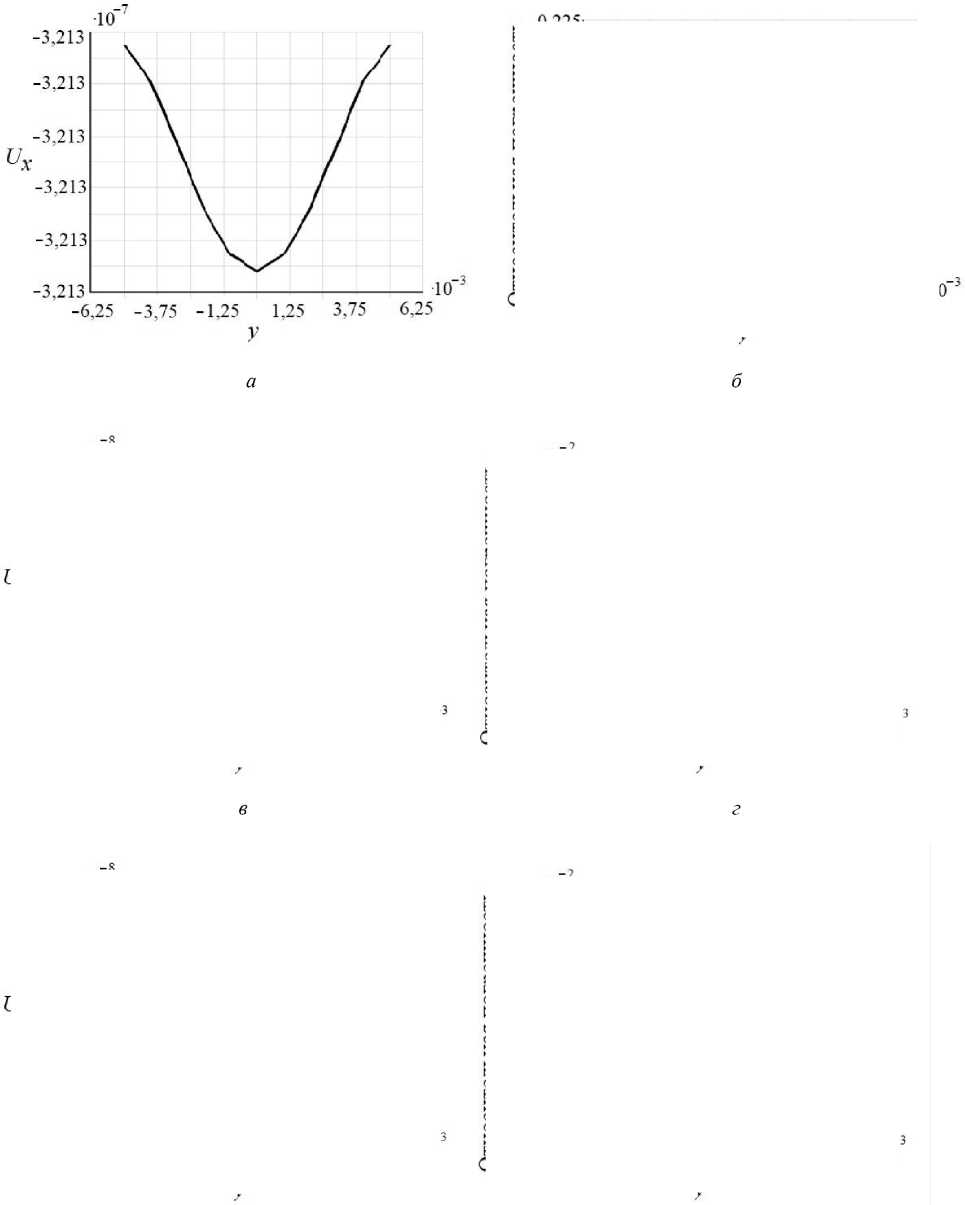
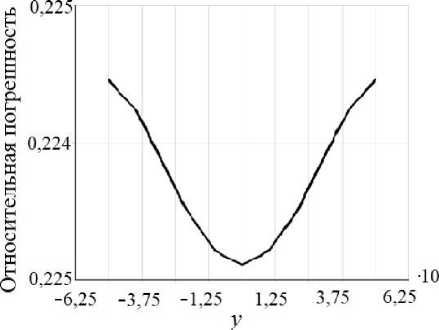
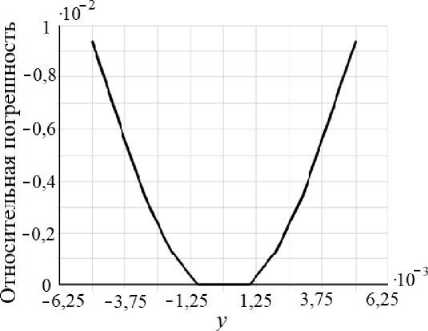
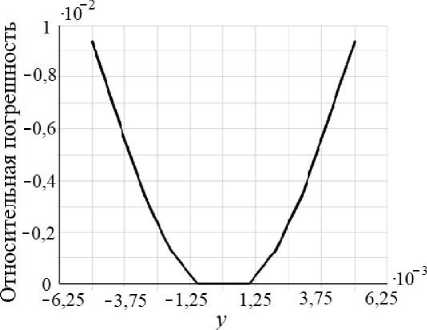
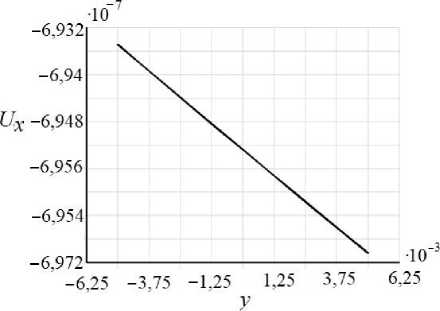
Рис. 3. Осевые перемещения ( а , в , д ) и относительная погрешность ( б , г , е ) численного решения в сечении x « l /2 (м), К_ц = 0, i , j = 1..3

е

Определяя перемещения путем интегрирования, получим

U = £xx + Cj, V = £y y + c2 ,     W = £zz + C3.(13)

Постоянные u ,v ,w определяются из условий закрепления u|x=0 = v|y=0 = wz=0 = 0 ^ cl, c2, C3 = 0 .(14)

Удовлетворяя им, получим u = £ Xx,   V = £ уУ, W = £ Zz.(15)

а

-.297E-05            -.209E-05             -.131E-05            -.522E-06

б

в

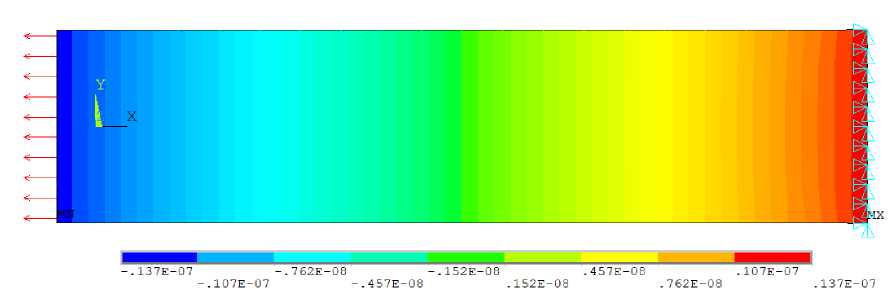
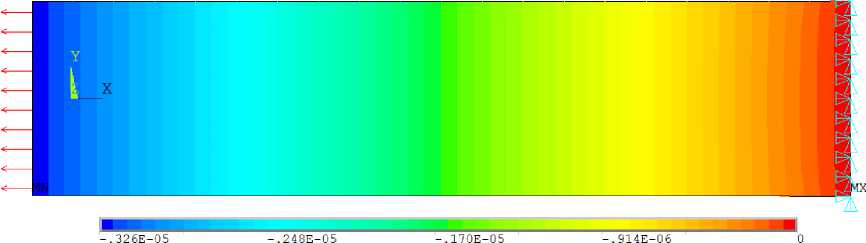
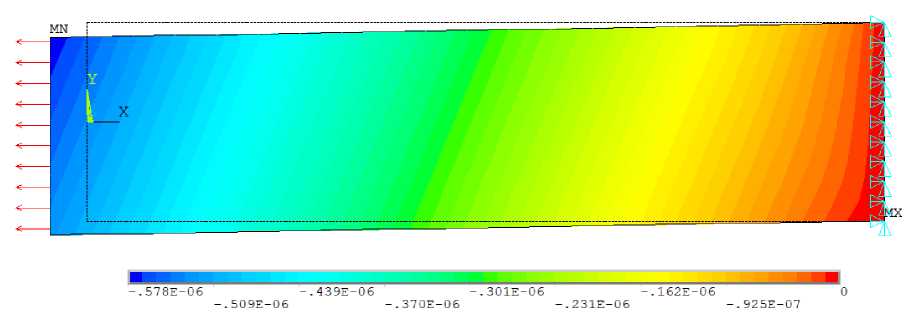
Рис. 4. Изолинии перемещений по оси x при: а - К_у = 0, i, j = 1...3;

б - K 11 = - 0,09, K 22 = - 0,05, K 33 = 0,14 ; в - K _u = - 0,09, K ₂₂ = - 0,05, K ₃₃ = 0,14, а = 64 °

Рассмотрим перемещения в поперечном сечении с координатой x = l /2 (рис. 3). На всех трех графиках относительная погрешность меньше 1%.

Несмотря на то что нагрузка равномерно распределена по краю, x = 0, перемещение балки вдоль этой оси происходит по параболе с максимальным отклонением от прямой линии, на три порядка отличающимся от величины самого перемещения (см. рис. 3, график U ), поэтому на рис. 4, а , б небольшое скругление сечений видно только вблизи заделки.

Рассмотрим контурные графики перемещений при задании различных компонент девиатора тензора структуры, в частности при его повороте на угол α (см. рис. 4, в ).

д

е

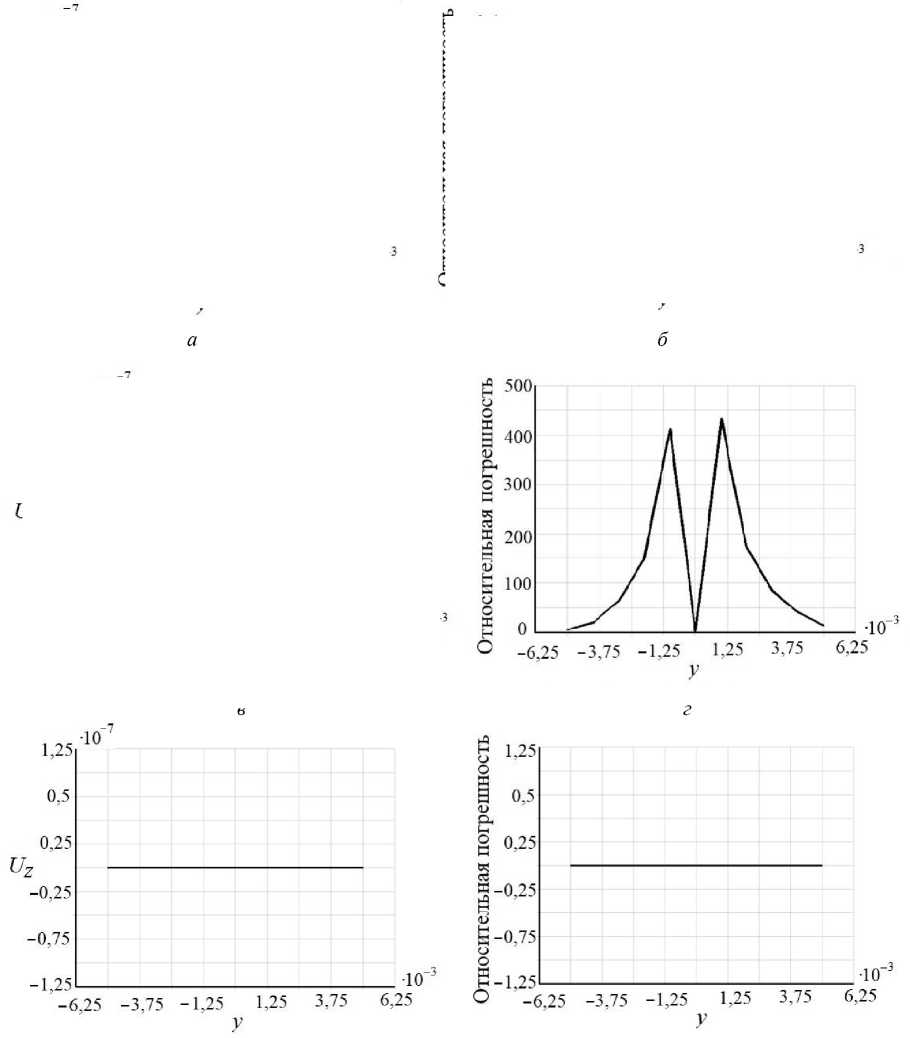
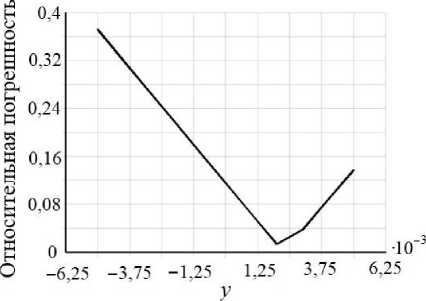
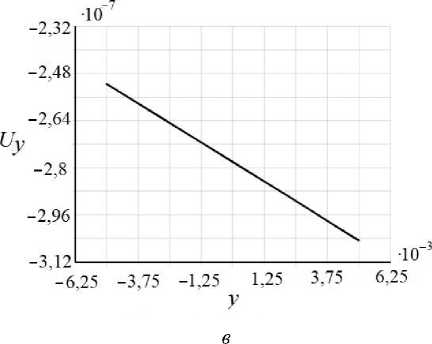
Р ис. 5. Осевые перемещения ( а , в , д ) и относительная погрешность ( б , г , е ) численного решения в сечении x * l /2 (м), K _n = - 0,09, K ₂₂ = - 0,05, K ₃₃ = 0,14

Аналитическое решение (15) говорит о том, что в общем случае анизотропии при растяжении стержень не только удлиняется в направлении силы и сокращается в поперечных направлениях, но еще и испытывает сдвиги во всех плоскостях, параллельных координатным [5]. Однако используемые в [5] формулы для деформации и перемещений в случае растяжения анизотропного стержня нельзя применять в данной задаче из-за сделанных изначально предположений (в частности, из-за предположения о плоском напряженном состоянии).

Рассмотрим поперечные сечения при анизотропии ( К_у ^ 0). В качестве аналитического решения используем соотношение (15).

Из графиков на рис. 5 видно, что перемещения U в значительной степени зависят от значений компонент тензора K , поэтому в случае анизотропии соотношение v = 8^ у применять неверно.

Отыскание параметров структуры

Решение второй задачи является ответом на вопрос: какой микроструктурой обладает кость, находящаяся в заданном напряженно-деформированным состоянии?

Исходные данные возьмем из решения предыдущей задачи, а именно значения компонент тензора напряжений и деформации. Требуется доказать, что К_у = 0 при i , j = 1...3 и e = - 0,0179. Для этого определяющее соотношение (2.1) преобразуется в систему

■                                                         л Т

111 г

⁸ x , ⁸ y ’ ⁸ z , 2 ⁸ yz ’ 2 ⁸ xz ’ 2 ⁸ xy f ,

Г                                               _t T X I

{ e , K 11 , K 22 , K 23 , K 13 , K 12 }   = A - у

	g 2 tr 8 + g 48 x	2( g 5 + g 6 )8 x + g 68 y	g 6 (8 y - 8 z )
	g 2 tr 8 + g 48 y	g 6 (8 x - 8 z )	2( g 5 + g 6 )8 y + g 68 x
где [ A ] = 6 - 6	g 2tr £ + g 48 z g 48 yz	- 2( g 5 + g 6 )8 z - g 68 y - g 58 yz	- 2( g 5 + g 6 )8 z - g 68 x 0
	g 48 xz	0	- g 58 xz
	.          g 48 xy	g 58 xy	g 58 xy          _

2 g 6 8 yz 2( g 5 + g 6 ) 8 yz 2( g 5 + g 6 ) 8 yz (8 y + 8 z )( g 5 + g 6 ) + g 6 8 x g 5 8 xy _             g 5 8 xz

2( g 5 + g 6 )8 xz               2( g 5 + g 6 )8 xy 2 g 6 8 xz                   2( g 5 + g 6 )8 xy 2( g 5 + g 6 )8 xz                   2 g 68 xy g 5 8 xz                            g 5 8 xy (8 x + 8 z )( g 5 + g 6 ) + g 5 8 xy               g 5 8 yz g 5 8 yz              (8 x + 8 y )( g 5 + g 6 ) + g 5 8 z _

Тогда e = - 0,0179; K_u = 0; K ₂₂ = - 1,3878 - 10 — ¹⁷; K ₁₃ = 0; K ₂₃ = - 1,3878 - 10 ^{- 17}; K ₁₂ = - 1,3878 - 10 ^{- 17}.

Точность решения А = 10 ^{- 16}.

Отыскание механических свойств материала

Задание K в определенном виде определяет тип упругой симметрии, реализуемый в материале. Когда К_у = 0, используя физическое соотношение для изотропного тела, можно найти технические константы E , v.

E (1 - v )             Ev              Ev                             (17)

--------------£   +-- £   +-- £   = G , (1 + v )(1 - 2 v ) ¹¹   (1 + v )(1 - 2 v ) yy (1 + v )(1 - 2 v ) ^zz xx

Ev           E (1 - v )             Ev

--------------£   +-- £   +-- £   = G , (1 + v )(1 - 2 v ) xx (1 + v )(1 - 2 v ) yy (1 + v )(1 - 2 v ) ^zz yy

E

-------£   = T . (1 + v ) xy xy

Тогда модуль Юнга и коэффициент Пуассона находятся по формулам

G„£- xx xyxx xy

, 2g_£  - T (£  + £  + £)

xx xy     xy xx      yy     zz

E = ^ x ^ ( 1 + v ) . ^ε xy

Заключение

Опираясь на кинетические уравнения феноменологической теории адаптивной упругости, предложенные S. Cowin для описания перестройки архитектуры трабекулярной костной ткани, вызванной выходом локальной деформации кости за пределы lazy zone (диапазон деформаций, внутри которого не происходит изменений в структуре), авторы предложили уравнения, позволяющие анализировать костную ткань (напряженно-деформированное состояние, структуру и пористость, упругие свойства материала) в гомеостазе. Сравнение аналитических решений с результатами расчета в ANSYS показало работоспособность математической модели.

Благодарности

Работа поддержана грантом Российского фонда фундаментальных исследований № 18-01-00589_а.