Бистабильное магнитомеханическое поведение ферромагнитных частиц в эластомерной матрице

Первыми технологически перспективными микрокомпозитами, структура и механические свойства которых обладают высокой чувствительностью к электромагнитным полям, были так называемые электрореологические (ER) жидкости [1, 2]. Хотя этот термин прочно закрепился в научно-техническом тезаурусе, трактовать его буквально и рассматривать указанные среды как однофазные жидкости

допустимо лишь относительно макроскопического масштаба. В действительности ER жидкости — это суспензии твёрдых частиц с характерным размером порядка единиц микрон в непроводящей жидкости. Компоненты суспензии подобраны таким образом, что диэлектрические проницаемости материала частиц и жидкой матрицы отличаются по величине. Под действием электрического поля в такой среде происходит обратимое агрегирование частиц, существенно изменяющее её макроскопическую гидродинамику и реологию.

Создание ER жидкостей и их быстрое продвижение в технологии явилось мощным стимулом для развития теории систем с дипольными и мультипольными взаимодействиями. В результате был разработан целый ряд аналитических и численных моделей для описания как равновесных структур, формируемых частицами в ER жидкостях под влиянием электрических и механических полей [3–5], так и отклика этих систем на переменные поля и нагрузки [6, 7].

Почти одновременно с возникновением ER жидкостей началась работа по изготовлению их магнитных аналогов — текучих сред, структуру и реологию которых можно контролировать с помощью магнитного поля. Так появились магнитореологические (MR) суспензии, где твёрдую фазу составляют микрочастицы ферромагнитных металлов или магнитодиэлектриков (ферритов) [8]. MR суспензии оказались более удобными в применении, в частности, потому, что медленноменяющееся магнитное поле не экранируется проводящими телами. Используя близкое формальное сходство уравнений магнито- и электростатики, теоретическая гидродинамика и реология MR сред позаимствовали многое из подходов, развитых для их ER аналогов.

Общий недостаток ER жидкостей и MR суспензий хорошо известен — это их склонность к расслоению/оседанию. В самом деле, для того чтобы обеспечить сильный отклик микродисперсной ER или MR системы на приложенное поле умеренной величины, частицы должны обладать значительными индуцированными моментами, то есть быть достаточно крупными: 1–10 мкм. Броуновское движение слабо влияет на такие частицы и, в частности, не предотвращает их гравитационное оседание (отрицательная плавучесть), обусловленное различием плотностей твёрдой фазы и жидкой матрицы. Расслоение ER и MR суспензий усиливается в неоднородных электрических и магнитных полях, поскольку влияние их градиентов на частицы аналогично действию дополнительной гравитационной силы.

Указанного недостатка лишены системы на основе полимерных гелей, когда частицы или химически «пришиты» к макромолекулярной сетке, или физически заключены в её ячейки. Именно так устроены композиты, называемые магнитореологическими полимерами и феррогелями. Внешнее поле поляризует частицы, и между их индуцированными магнитными моментами возникают магнитные (пондеромоторные) силы притяжения/отталкивания, стремящиеся организовать частицы в структуру, отвечающую минимуму магнитостатической энергии. Однако в MR полимере этой тенденции противодействуют упругие силы, которые возрастают по мере удаления частиц от их исходных положений внутри сетки. Таким образом, чтобы найти макроскопический (наблюдаемый) отклик MR полимера на приложенное поле, необходимо выяснить, как устанавливается баланс магнитных и упругих сил в этой системе на мезоскопическом уровне.

Расчёт взаимодействия частиц в MR композитах отличен от своего ER аналога. Дело в том, что связь между поляризацией и электрическим полем, действующим внутри частицы, в любых реальных условиях можно считать линейной: P = ( б p - 1 ) E /( 4 п ) . Здесь б p — диэлектрическая проницаемость материала частиц; она не зависит от величины поля и по порядку величины не превышает 10. При б p = const уравнение, описывающее распределение электростатического потенциала ф в системе диэлектрических частиц, погружённых в матрицу с диэлектрической проницаемостью б , принимает вид уравнения Лапласа ( Аф = 0), а его граничные условия оказываются линейными. В этом случае задача имеет точное, хотя и очень громоздкое, решение для системы из произвольного числа частиц [4].

Магнитным наполнителем MR систем служат микрочастицы ферромагнетика, чаще всего железа. В отсутствие магнитного поля такие частицы многодоменны, вследствие чего магнитный момент у них отсутствует. В относительно слабых полях главным механизмом намагничивания является рост «выгодных» доменов. В этом режиме намагничивание материала частицы можно, хотя и грубо, аппроксимировать линейным законом M = x p "H при значениях начальной магнитной восприимчивости х Р ⁰⁾ ~10 3 - 10 5 ед. СГСМ [9]. В полях умеренной напряжённости рост величины M = M ( H ) существенно замедляется, а затем происходит насыщение: M ^ M s = const( H ). В литературе для описания нелинейного намагничивания многодоменных образцов железа часто используется эмпирическое соотношение Фрёлиха–Коннелли [9–11], которое определяется двумя введёнными выше материальными параметрами х Р⁰⁾ и Ms :

M ( H ) =

x P M s H M s +X 0 H

x P⁰⁾H               при x P⁰⁾H <<  Ms ,

M s ( 1 ^- M s /( x P^0)H ) ) при x P⁰⁾ H » M s ;

здесь и далее намагничивание частиц предполагается изотропным. Очевидно, что закон намагничивания (1) эквивалентен введению нелинейных магнитных восприимчивости и проницаемости:

χ (0) M

χ p ( H ) = _M + ^p (0 ^s ) _H ,    µ p ( H ) = 1 + 4 πχ p ( H ).

_s +χ _p

В непроводящей среде магнитное поле является безвихревым (rot H = 0), что позволяет ввести магнитостатический потенциал согласно H = - ∇ ψ . Однако при нелинейном законе намагничивания подстановка магнитной индукции в условие соленоидальности div B = 0 приводит вместо уравнения Лапласа к нелинейному уравнению

∆ψ = -∇ψ ⋅∇lnµp (-∇ψ), (3)

конкретный вид которого обуславливается зависимостью магнитной проницаемости материала от напряжённости приложенного поля. Нелинейным характером обладают и условия, которым должен удовлетворять магнитостатический потенциал внутри ( i ) и снаружи ( e ) границы Γ каждой частицы:

_ψ ( i ) _{Γ =ψ} ( e ) _{Γ ,     µ p ( -∇ψ} ( i ) ₎ ∂ _∂ ψ _n ^{( i )}

∂ψ ^{( e )}

=µ Γ∂n

,

Γ

где µ — магнитная проницаемость среды (полимерной матрицы), а n — внешняя нормаль к поверхности.

Нелинейность намагничивания частиц (см. уравнения (3) и (4)) — принципиальная особенность MR полимеров. По этой причине точные (линейные) решения уравнения Лапласа, которыми исчерпывается случай ER композитов [4], могут быть полезны для MR систем только в области начального намагничивания ( х ^⁰’H ^ Ms ), где ферромагнетик можно уподобить парамагнетику.

2.    Магнитные поля в системе из двух частиц

Для мезоскопической механики MR полимеров задача, рассматривающая взаимодействие, которое возникает между двумя частицами из магнитомягкого ферромагнетика в постоянном внешнем поле H ₀ , имеет фундаментальное значение. Хорошо известно решение, полученное в парамагнитном приближении, когда намагниченность прямо пропорциональна напряжённости поля [3, 4, 7, 12–14]. Однако магнитный отклик феррочастиц, которыми наполнены реальные MR системы, можно считать линейным только в относительно слабых полях. С возрастанием величины поля приращения намагниченности уменьшаются, стремясь к нулю, когда ферромагнетик входит в режим насыщения. Поскольку энергия взаимодействия частиц U_mag пропорциональна квадрату их магнитных моментов, ясно, что для описания межчастичных сил — они определяются производными U_mag — в широком диапазоне полей необходимо построить выражение для парной энергии, учитывающее нелинейность намагничивания ферромагнетика.

В силу того, что типичным материалом микрочастиц, которыми наполняются MR эластомеры, служит железо, для закона нелинейного намагничивания естественно выбрать форму Фрёлиха–Коннелли (1). После введения безразмерных напряжённостей внутреннего ( H ) и внешнего ( H0 ) по отношению к частице полей h=H Ms,  h0=H0Ms уравнение (1) принимает вид:

χ(0) χp m = χph,   χp=1+χ(0)h, где m= M(H)Ms — безразмерная намагниченность, h = h . Магнитостатический потенциал задаётся в таком виде, что он измеряется в единицах Ms и включает в себя вклад однородного внешнего поля:

h = -∇ψ .

Введённая функция ψ ( r ) определена в бесконечном пространстве, окружающем частицы, и удовлетворяет граничным условиям (4) на поверхности каждой из них .

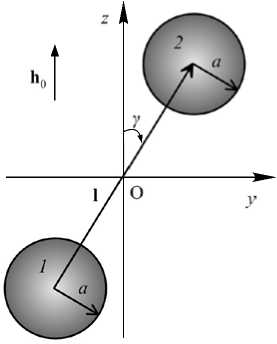
Рис. 1. Выбранная для решения задачи система координат

Пусть две одинаковые сферические частицы радиуса а погружены в немагнитную ( ц = 1) матрицу, а их центры отстоят друг от друга на расстояние l . Вектор l проведён от частицы 1 к частице 2 и составляет угол у с направлением поля h ₀. Вид системы координат представлен на рисунке 1, её центр совмещён с центром масс пары, ось O z направлена вдоль h ₀ , а плоскость O yz проходит через вектор l . При взятии a в качестве единицы длины межцентровое расстояние вычисляется как q = //а , так что значение q = 2 соответствует плотному контакту частиц.

Для численного решения уравнений (3), (4) применён итерационный алгоритм, представляющий нелинейную задачу в виде последовательности линейных задач. Магнитостатический потенциал рассчитывается в конечной кубической области пространства со стороной d = к(/ + 2а), где к »1 — числовой коэффициент. Вне расчётной области потенциал ^(r) задаётся как сумма потенциалов точечных диполей, магнитные моменты которых равняются магнитным моментам частиц, найденным на предыдущей итерации.

В начале расчёта функция х p ( r ) (она отлична от нуля только внутри частиц) полагается однородной и имеющей начальное значение х Р ⁰⁾• В этом приближении находится потенциал ^ ( r ), дифференцирование которого (см. (7)) даёт напряжённость поля h ( r ). По её распределению внутри частиц с помощью (6) строится следующее приближение функции х p ( r ) для нового шага цикла. Таким образом, каждая итерация представляет собой решение линейной задачи магнитостатики для системы с пространственнонеоднородной восприимчивостью. Вычисление х p ( r ) продолжается до тех пор, пока намагниченности частиц m ( r ) не перестают изменяться.

Компьютерный код, реализующий указанный алгоритм, написан на языке python с использованием библиотеки esys.escript, предназначенной для решения трёхмерных задач методом конечных элементов. Вычислительная сетка сгущается в областях, где предполагаются наибольшие градиенты потенциала. Так, размер ст 1 элемента на поверхностях частиц, обращённых друг к другу, берётся существенно меньшим по сравнению с размером ст ₂ элемента на «удалённых» поверхностях частиц. При этом ст ₂ ^ ст ₃, где ст ₃ — размер элемента сетки на границе расчётной области. Путём варьирования параметров ст i ( i = 1,2,3 ) и к подбиралось оптимальное соотношение между точностью решения и доступными вычислительными ресурсами. Расчёты проводились на суперкомпьютере «Уран» в ИММ УрО РАН (г. Екатеринбург).

3.    Магнитные силы взаимодействия

Магнитостатическая задача (3), (4) решалась в широком диапазоне как значений геометрических параметров пары / и у , так и приложенного поля h ₀ при начальной восприимчивости х Р ⁰⁾ = 10 3 - Из этого решения по формуле

^U _m a _g ( m ■ h  m ■ h o

M 2     ‘^    2      2

+

h

J m ■ dh I dV = J ---- o J           2

m ■ h,

х

p

—

—

|hi ^— ln ( х р ⁰⁾ I^h| ⁺ 1 ) v°)

^х p

)

■ dV ,

полученной из общего соотношения [15], рассчитана энергия взаимодействия пары частиц. Интегрирование в (8) ведётся по суммарному объёму частиц. Результатом является дискретный массив значений U_mag ( l , y ).

Силы магнитного (пондеромоторного) взаимодействия частиц могут быть выражены с помощью производных магнитной энергии:

f = f n + f ,

1 (  d U f = — 2 i--mag "       l2 I       dl

f =i 1 ^{1 x}l ^{1 x}

d U mag

d l

Как видно, вектор f _n параллелен вектору l и определяет силу притяжения/отталкивания частиц. Другая составляющая силы — f _τ , перпендикулярна l и лежит в плоскости, содержащей векторы h ₀ и l , а пара сил f _τ создаёт вращающий момент

М = l х fT = - l xd Umag (ЭХ ,    M = -d Umag pY, , стремящийся ориентировать межцентровой вектор l вдоль направления поля h0 .

Наиболее простая и часто употребляемая модель, описывающая силы магнитного взаимодействия частиц, — это приближение точечных диполей, которое справедливо в случае q = l/а » 1. Поэтому оно вполне оправдано для таких MR систем, где концентрация частиц мала, а их распределение однородно. В плотных MR полимерах большинство частиц сближено настолько, что расстояния между ними оказываются порядка их характерного размера: q >  2 . Для этой ситуации приближение точечных диполей непригодно, поскольку значительный вклад в межчастичные силы вносят неоднородности намагничивания частиц, обусловленные их взаимным влиянием. В случае линейной поляризации ( χ _p = const) указанная задача во всём интервале 0 ≤ q ≤∞ может быть решена точно в терминах мультипольного разложения [4].

Как и следовало ожидать, различия между предсказаниями линейных моделей — дипольной и мультипольной — увеличиваются по мере сближения частиц ( q → 2) , и при плотном контакте вычисляемые величины могут отличаться в десятки раз [5, 13, 16]. Однако общим свойством этих решений является квадратичный рост силы f _n , f _τ ∝ h ₀ ² независимо от порядка мультипольного приближения. Как указано выше, для реальных MR полимеров предположение о линейности намагничивания может быть использовано только в слабых полях и обязательно нарушается при h 0 >  1, когда зависимость х p ( h ) становится существенно нелинейной.

Насыщение намагниченности означает и насыщение межчастичных сил: они перестают зависеть от величины приложенного поля. Это поведение иллюстрируют рисунки 2 и 3, где представлены результаты расчёта межчастичных сил в зависимости от h ₀ , а параметром служит межцентровое безразмерное расстояние q . На этих графиках сплошными линиями показаны результаты выполненного численного расчёта с учётом насыщения намагниченности, а параболические кривые (пунктирные линии) соответствуют решениям в приближении линейного намагничивания при числе мультиполей около 100. Штриховые линии получены из упрощённой модели насыщения, где уравнение магнитного состояния имеет вид (6), но частицы считаются точечными диполями [17]. Это приближение, назовём его моделью нелинейных взаимодействующих диполей (НВД), — модификация аналогичных моделей взаимодействия, введённых для ансамблей парамагнитных частиц [12, 14].

мультипольное приближение при линейном намагничивании, штриховые – модель НВД

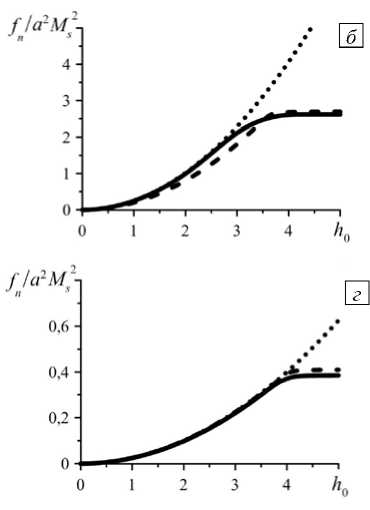
Рис. 2. Силы притяжения частиц в положении «голова–хвост» ( γ= 0 ° ) в зависимости от приложенного поля для межцентровых расстояний q : 2,05 ( а ); 2,5 ( б ); 3 ( в ); 4 ( г ); сплошные линии – численное решение, пунктирные –

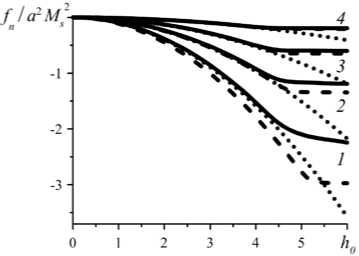
Рис. 3. Силы отталкивания частиц в положении «бок–о–бок» ( у = 90 ° ) в зависимости от приложенного поля для межцентровых расстояний q = 2,05 (кривая 1 ), 2,5 ( 2 ), 3 ( 3 ) и 4 ( 4 ); сплошные линии – численное решение, пунктирные линии – мультипольное приближение при линейном намагничивании, штриховые – модель НВД

Как видно из рисунка 2, в положении «голова-хвост» ( у = 0 ° ) насыщение намагниченности, связанное с взаимным влиянием частиц, может быть очень значительным. Например, при q = 2,05 линейное мультипольное приближение нарушается уже при h ₀ <  1 (Рис. 2 a, пунктирная линия). Из этого же рисунка видно, что на малых межчастичных расстояниях непригодна и модель НВД, которая учитывает насыщение намагниченности в предположении об однородности последней. Поскольку сила магнитного притяжения быстро уменьшается с ростом межчастичного расстояния, то масштабы графиков по вертикальным осям различны.

В случае, когда частицы расположены не слишком близко друг к другу (q > 3 ), все решения хорошо согласуются между собой вплоть до области

перехода намагниченности от возрастания к насыщению. При дальнейшем росте напряжённости поля модель НВД продолжает близко следовать за численным решением, в то время как приближение линейного намагничивания начинает завышать величину межцентровой силы. Однако, как показывает рисунок 3, для сил отталкивания ( у = 90 ° ) модель НВД вполне приемлема уже при q >  2,5 .

Сравнение рисунков 2 и 3 показывает, что силы взаимодействия частиц в положениях «голова-хвост» и «бок-о-бок» насыщаются при различных значениях поля. Так, например, для q = 2,5 сила притяжения достигает наибольшего значения при h0 ~ 3,5 (Рис. 2), но при этом сила отталкивания составляет лишь около половины максимально возможной (Рис. 3). Подобное поведение сил имеет простое объяснение: в положении «голова-хвост» взаимное влияние частиц усиливает поля внутри них и тем самым приближает намагниченность к насыщению; в положении «бок–о–бок» магнитное взаимодействие частиц уменьшает внутренние поля, снижая тем самым намагниченность.

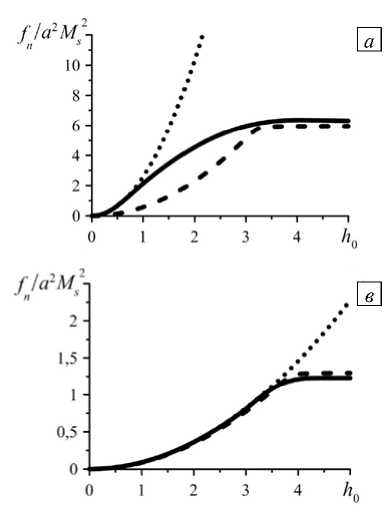
Вследствие нелинейности задачи сила межчастичного взаимодействия при промежуточных значениях у не является точной суперпозицией указанных выше предельных случаев и для любого угла должна рассчитываться отдельно. Рисунок 4 иллюстрирует один такой случай: у = 45 ° . Как видно, для частиц, находящихся друг от друга на расстоянии q >  3, модель НВД очень хорошо аппроксимирует численное

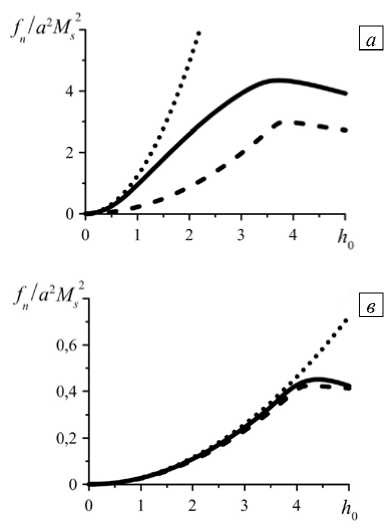
Рис. 4. Силы притяжения частиц в положении у = 45 ° в зависимости от приложенного поля для различных межцентровых расстояний q : 2,05 ( а ); 2,5 ( б ); 3 ( в ) и 4 ( г ); сплошные линии – численное решение, пунктирные линии – мультипольное приближение при линейном намагничивании, штриховые линии – модель НВД

решение (см. Рис. 4 в и 4 г ). Это означает, что неоднородности намагниченности, вызванные взаимным влиянием частиц, весьма малы. Если же частицы находятся в достаточно близком соседстве, между численным решением и моделью НВД в области умеренных полей прослеживается лишь качественное сходство (см. Рис. 4 а и 4 б ). Соответственные кривые (сплошная и штриховая) асимптотически сближаются только в сильных полях, где частицы намагничены однородно и, таким образом, неотличимы от точечных диполей. Рисунок 4 указывает также на немонотонность функции f_n ( h ₀): сила притяжения достигает максимума при конечном значении поля, а затем убывает. Эта особенность, которую обнаруживают как численный расчёт, так и модель НВД, есть результат конкуренции двух противоположных эффектов: увеличения магнитного момента каждой из частиц и их взаимного размагничивания; более детальное объяснение дано в работе [17].

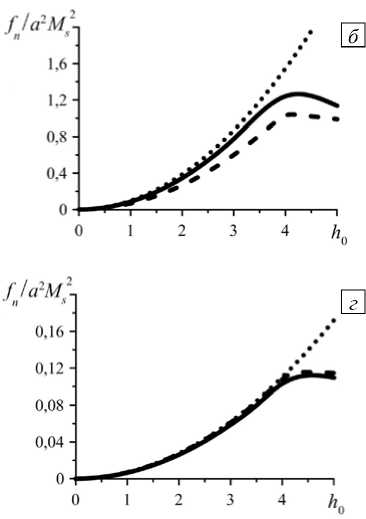
расстояния в поле h ₀ :

Рис. 5. Силы притяжения частиц в положении «голова–хвост» в зависимости от межцентрового

1 ( а ); 2 ( б ); 3 ( в ); 4 ( г ); сплошные линии – численное решение, пунктирные – мультипольное приближение при линейном намагничивании, штриховые – модель НВД

Рисунок 5 содержит кривые парных сил в конфигурации «голова–хвост» как зависимости от межчастичного расстояния. Графики показывают, что при учёте насыщения применимость той или иной аппроксимации обуславливается величиной приложенного поля h ₀ . Так в поле, далёком от насыщения,

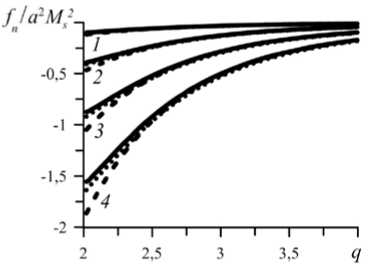
Рис. 6. Силы отталкивания частиц в положении «бок – о – бок» в зависимости от межцентрового расстояния в магнитном поле с h ₀ : 1 (кривая 1 ), 2 ( 2 ), 3 ( 3 ), 4 ( 4 ); сплошные линии – численное решение, пунктирные – мультипольное приближение при линейном намагничивании, штриховые – модель НВД

сближение частиц влечёт за собой рост локального поля h и, как следствие, заметный рост намагниченности. По этой причине модель линейно намагничивающихся частиц (пунктирные линии) неплохо описывает точное решение (см. Рис. 5 а ). В сильном внешнем поле, которое само по себе насыщает намагниченность, — ситуация, показанная на рисунках 5 в и 5 г — хорошим приближением для точного расчёта становится модель НВД (штриховые линии).

В положении «бок–о–бок» (см. Рис. 6) даже, казалось бы, сильное внешнее поле внутри частиц ослабляется настолько, что переход к насыщению намагниченности заметно «откладывается». В результате во всём изученном интервале полей модель, предполагающая линейное намагничивание частиц (пунктирные линии), неплохо описывает точное решение.

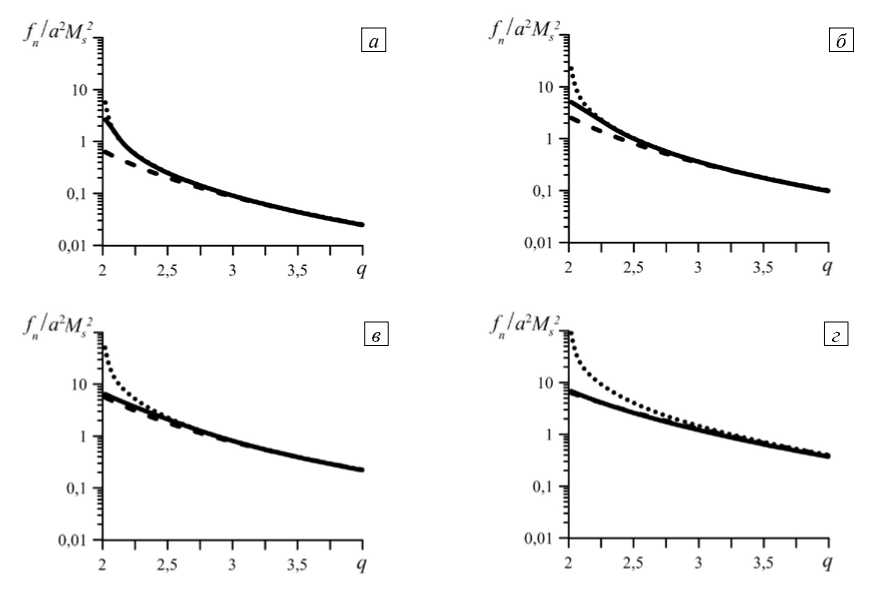
а

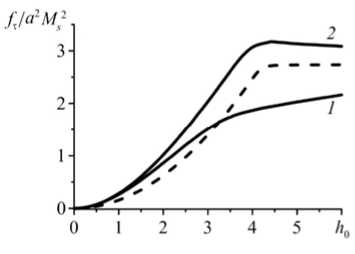
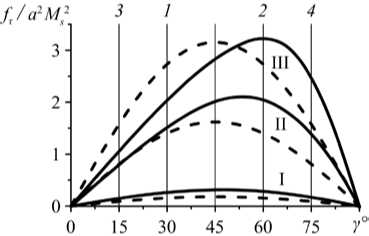
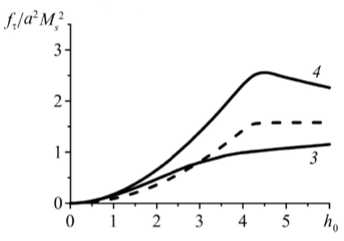
Рис. 7. Результаты численного расчёта касательной силы f . при q = 2,02 ; угловая зависимость для полей h ₀ : 1 (кривая I); 3 (II); 5 (III) ( a ); зависимость от величины внешнего поля: сплошные линии – численное решение для углов 30 ° (линия 1 ) и 60 ° ( 2 ), штриховая линия – результат по модели НД для f . (45 ° + 15 ° ) ( б) при углах у = 15 ° (линия 3 ) и 75 ° ( 4 ); штриховая линия – результат согласно модели НД для f _: (45 ° + 30 ° ) ( в)

в

Насыщение намагниченности нетривиально влияет на касательную компоненту f . межчастичной силы. Как известно, в случае линейного намагничивания частиц угловая зависимость парной энергии магнитного взаимодействия подчиняется закону cos ² у [7, 13], то есть остаётся той же, что для пары нелинейных диполей (НД) [17] или пары частиц с постоянными магнитными моментами. Таким образом, для всех указанных моделей функция f . ( у ) к sin2 y достигает максимума при у = 45 ° и является чётной относительно этого значения. Однако в частицах, намагничивающихся с насыщением, указанная симметрия отсутствует. Рисунок 7 а представляет угловую зависимость f . при различных значениях поля. Из него отчётливо видно, что максимум f . располагается вблизи у = 45 ° только в слабом поле; с ростом последнего максимум кривой монотонно смещается в сторону бóльших углов (см. кривые II и III на Рис. 7 а ).

Чтобы пояснить причину нарушения угловой симметрии, рассмотрим значения f . для углов, равноотстоящих от у = 45 ° , например, ( 15 ° ,75 ° ) и ( 30 ° ,60 ° ) . На рисунке 7 а эти углы отмечены вертикальными линиями, а соответствующие им зависимости f . от величины поля представлены на рисунке 7 б (для у = 15 ° ,75 ° ) и 7 в (для у = 30 ° ,60 ° ). В слабом поле ( h 0 <  1) частицы мало влияют друг на друга, и значения f . (45 °± Д у ) практически совпадают. При повышении поля в парах частиц, имеющих ориентацию у <  45 ° , взаимное намагничивание ускоряет переход к насыщению, а в парах с у >  45 ° замедляет его. Это видно из того, что на рисунках 7 б и 7 в параболические участки кривых для ориентаций у >  45 ° заметно протяжённее, чем их «аналоги» из интервала у <  45 ° .

Для сравнения на рисунках 7 б и 7 в штриховыми кривыми изображены зависимости f . (45 °± Д у ), рассчитанные по модели НД, которая не учитывает изменение магнитных моментов, вызванное их взаимовлиянием. К такой схеме обсуждаемая задача сводится в пределе сильного поля, когда намагниченность каждой из частиц полностью насыщается и магнитный момент становится постоянным по величине: ц = M s V . Как видно, угловая асимметрия функции f . ( у ) отсутствует во всём диапазоне полей при h ₀ >  4 л/ 3. Примечательно, что угловая симметрия f . ( у ) сохраняется не только в простой модели НД (частицы считаются точками), но и в модели с неоднородным распределением намагниченности, если только частицы парамагнитны (магнитная восприимчивость % постоянна) [13].

Сопоставление этих фактов с результатами численного расчёта, представленными на рисунках 7 б и 7 в , приводит к выводу, что нарушение симметрии f . ( у ) (расхождение сплошных кривых) есть следствие специфических неоднородностей намагничивания, которые возникают вследствие «неполного» насыщения намагниченности внутри частиц. Конкретно речь идёт о ситуациях, когда под действием неоднородного внутреннего поля некоторая доля объёма частицы уже насыщена (то есть намагничена однородно), в то время как для остального объёма насыщение ещё не наступило (очевидно, что в парамагнитных частицах такие состояния невозможны.) В случае, представленном на рисунке 7, частицы расположены очень близко, и их взаимное влияние значительно. Поэтому асимметрия f . ( у ), приводящая к расхождению линий на рисунках 7 б и 7 в , проявляется уже в относительно слабых внешних полях.

4.    Взаимодействие частиц через упругую матрицу

В разделе 3 рассмотрены силы, возникающие между частицами изотропного ферромагнетика при намагничивании. В MR эластомере, наполнителем которого являются такие частицы, в результате их смещений под действием магнитных сил эластомерная матрица деформируется, в ней возникают упругие напряжения, которые порождают силу противодействия (возвращающую силу), приложенную к частице. В системе двух частиц поля напряжений, созданные каждой из них, взаимодействуют (в общем случае нелинейно), так что возвращающая сила, приложенная к одной частице, содержит вклад, обусловленный другой из них. В этих условиях удобно ввести эффективный парный потенциал упругого взаимодействия частиц, параметры которого определяются через характеристики материала матрицы.

Пусть две сферические частицы радиуса a помещены в эластомерный цилиндр, ось которого совпадает с вектором l пары; в отсутствие поля расстояние между центрами частиц составляет l ₀ . Цилиндрическая система координат ( О рф z ) выбрана таким образом, что её ось O z направлена по оси модельного «двухчастичного» MR эластомера. В этой системе перемещение частицы 1 задаётся вектором u 1 = (0,0, - v_p ), а частицы 2 — вектором u ₂ = (0,0, v_p ), так что накапливаемая упругая энергия U_d зависит только от величины смещения v_p .

В качестве модели эластомерной матрицы, в которую заключены частицы, взята среда Муни–Ривлина — хорошо известное приближение, успешно справляющееся с описанием конечных деформаций в механике эластомеров [18]. В предположении несжимаемости среды упругий потенциал Муни–Ривлина можно представить в виде:

W ( C ) = W ( C )/ c = [ I 1 ( C ) - 3 ] + c [ 1 2 ( C ) - 3 ] , (10)

где c 1 и c₂ = c 2 / с 1 = 0,2 — материальные константы; 1 1 , 1 2 — инварианты тензора деформации Коши-Грина C , выражаемого через поле перемещений u с помощью градиента в отсчётной конфигурации: C = ( I +V u ) - ( l + V u T ) , здесь I — единичный тензор, Т — символ операции транспонирования.

Для расчёта упругой энергии, накапливающейся в «двухчастичном» MR эластомере при смещении частиц внутри него, была написана программа на языке python с включением библиотеки fenics, реализующей метод конечных элементов [19]. Вариационная задача деформирования образца из упругого несжимаемого материала была сформулирована в отсчётной конфигурации:

Js[W - P (J -1)] dV = 0,

« 0

где Q₀ — начальный объём образца, W — упругий потенциал, P — среднее давление, J = ^ I ₃ ( C ) .

Симметрия инверсии образца относительно оси O z (см. Рис. 1) даёт возможность решать задачу только в половине образца ( z >0) и рассматривать, таким образом, лишь одну частицу — сферу радиуса a с поверхностью Г и граничными условиями для поля перемещений:

u р 1 р =0 = 0, u z I z =0 = 0,    ^u | Г = ^u 1 = ⁽⁰,0, ^- v p );

последнее из условий обеспечивает смещение частицы как абсолютно твёрдого тела.

Величина перемещения v _p изменялась дискретно от нуля до v m“ = ( 12 ) 1 ₀ - a , то есть до плотного контакта частиц. На каждом шаге по v _p задача нелинейной упругости решалась методом Ньютона, начальным приближением служило решение, найденное на предыдущем шаге. Результатами расчёта были поле перемещений, в том числе величина v — смещение торцов вмещающего частицы цилиндра вдоль O z , и среднее давление. По этим данным вычислялись мера деформации Коши–Грина и, при подстановке её инвариантов в (10), — объёмная плотность энергии W . В итоге формировался дискретный массив U l ( q , q о ) , определяющий зависимость упругой энергии образца U_e1 = J WdV от безразмерных значений начального ( q ₀ = 1 ₀/ а ) и конечного ( q = 1/а ) расстояний между центрами частиц. Полученные результаты использовались далее для построения и верификации интерполяционной формулы, позволяющей рассчитывать функцию U_el при любых значениях q ₀ и q , что существенно облегчило все дальнейшие расчёты.

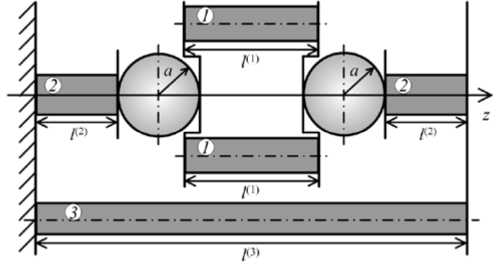
Рис. 8. Стержневая модель для интерполяции упругой энергии

Указанная интерполяция основана на эвристической схеме, представленной на рисунке 8. Моделью «двухчастичного» MR образца служит механическая ячейка, содержащая две твёрдые сферические частицы и набор упругих стержней из несжимаемого полимера Муни– Ривлина. Ячейка имеет размер l(3) , задаваемый положением внешних стенок, неподвижной — слева, и подвижной — справа. Каждая частица заключена между двумя абсолютно жёсткими пластинами (одна из них обладает ступенчатой формой), к которым прикреплены стержни. В зазоре между частицами расположены   два одинаковых цилиндрических стержня радиусами r1 и длинами I01) >(q0 - 2) a ; и пластины обеспечивают однородное сжатие/растяжение внутренних стержней при деформировании по оси Oz . Частицы соединены с внешними стенками ячейки стержнями радиуса r2 и длинами l0(2) . Параллельно цепочке частиц между стенками ячейки вложен ещё один стержень радиуса r3 и длины 103) = 2a + q0a + 2102) . При сближении частиц «внутренние» стержни (стержни 1) будут сжиматься, а «периферийные» (стержни 2) — растягиваться; при этом ячейка в целом будет сжиматься. Относительные удлинения стержней простым образом выражаются через заданное смещение частиц vp и удлинение всей системы v = 103) -1(3):

₌ ¹ 01) ^{- 2} V p ₌ ,4   .   ₌ 1 0²⁾ —А 1 ^{(2)    1} 02) ⁺ ( v ^- v p )      v - v p         1 0³⁾ - 2 v _2 v

' 1           ,(1)            ¹      ,(1) , ^X 2            ,(2)                      ,(2)                ¹        ,(2)     ,     ^X 3          ,(3)          ¹     ,(3) .

0     0      0      0      0      00

Уравнения связи (11) позволяют вычислить инварианты меры деформации Коши – Грина согласно формулам:

11(Ck) = 2/Xk + X2 ,   12(Ck) = 1/X2 + 2Xk (k = 1, 2, 3), а затем по формуле (10) — упругий потенциал каждого стержня. Общая упругая энергия системы будет иметь вид:

UjC 1 = ; V (2 -8 k ^ ( C k ) r k 1 0 k ) ,                              (12)

k = 1

где r_k и l ₀ ^{( k )} — радиусы и начальные длины стержней соответственно.

Расчёты выполнялись для значений межцентровых расстояний частиц из интервала 2,1 <  q 0 <  6 при фиксированной полной начальной длине образца 1 0³⁾ / а = 12. Радиусы всех стержней и длина «внутренних» из них — l ₀ ⁽¹⁾ , рассматривались как подгоночные параметры и подбирались по критерию наилучшего согласия между модельной функцией (12) и массивом данных об упругой энергии, полученным численным расчётом. Значения интерполяционных коэффициентов, соответствующие некоторым значениям начального межцентрового расстояния, представлены в таблице. При их использовании аппроксимация (12) воспроизводит результаты вычислений U_el ( q , q 0 ) в области q 0 >  2,1 c погрешностью не более 1%. С учётом этого факта формула (12) была применена также для экстраполяции функции U_e1 ( q , q 0 ) в область 2,02 <  q 0 <  2,1, где прямой численный расчёт теряет устойчивость.

Таблица. Числовые параметры интерполяции

q 0	r 1 a	r 2 a	r 3 a	l 0 (1)   a
2,5	4,974	0, 4779	8, 442	0, 701
3	4,198	0,5086	7, 219	1,362
3,5	3,950	0, 4683	6, 656	1,926
4	3,801	0, 4763	5,929	2,534

5.    Магнитомеханический гистерезис пары частиц

Объединение магнитного (8) и упругого (12) вкладов даёт выражение энергии пары намагничивающихся частиц, находящихся в эластомере в конфигурации «голова-хвост» (относительно поля Н ₀), вида:

U ( h 0 , q , q о ) = U mag ( h 0 , q )| + Ue,(q , q 0 ), (13)

где h ₀ = H _o I Ms . Поскольку материал частиц намагничивается нелинейно, то функция U_mag зависит от параметров х р" и M s (см. формулу (1)). Минимизация энергии U по q при заданных значениях внешнего поля h ₀ и начального межцентрового расстояния q ₀ обуславливает равновесный размер пары в намагниченном состоянии, а появление более чем одного минимума означает мультистабильность системы.

В работе [13] анализировались функции U ( h ₀, q , q ₀) для пары частиц из линейно намагничивающегося, то есть парамагнитного материала. Показано, что в определённом интервале полей такая система проявляет бистабильность: для энергии свойственны два минимума, локализованных при различных значениях q , одно из которых соответствует близкому соседству частиц ( q - 2). При усилении поля до некоторой величины h 0¹⁾ бистабильность исчезает, и состояние равновесия при q - 2 становится единственным. Это означает, что выше порога h ⁽¹⁾ происходит образование двухчастичного кластера. Эффект имеет гистерезисный характер: кластер, возникший в поле h 01) , при снижении величины поля до значения h 0²⁾ <  h 0¹ распадается, то есть в системе наблюдается переход первого рода. Для парамагнитных частиц ширина области магнитомеханического гистерезиса h 0¹ - h 0²⁾ неограниченно растёт с увеличением q ₀.

Функция (13) даёт возможность впервые изучить вопрос о магнитомеханическом гистерезисе в паре ферромагнитных, а не парамагнитных, частиц и тем самым сделать важный шаг на пути к построению мезоскопической теории реальных MR систем.

Перед обсуждением количественных результатов полезно качественно проанализировать магнитомеханический отклик пары ферромагнитных частиц. Пусть частицы находятся в плотном контакте, то есть q * - 2. Поскольку в режиме насыщения энергия U_mag достигает максимума и перестаёт зависеть от приложенного поля, то при любом начальном размере пары q ₀ выигрыш магнитной энергии не может превышать конечную величину A U_mag = | U_mag ( да , q *)| , где формально положено h ₀ = да . Вместе с тем приращение упругой энергии A U el = U el ( q * , q ₀) не зависит от поля и неограниченно растёт с увеличением q ₀ . Отсюда следует, что для ферромагнитных частиц (в отличие от парамагнитных) интервал значений q ₀ , где магнитная и упругая энергии могут конкурировать между собой, создавая бистабильность, ограничен сверху некоторой величиной q Up . Последняя тем больше, чем выше намагниченность насыщения ферромагнетика M_s и ниже упругость материала, характеризуемая параметром с 1 потенциала Муни-Ривлина.

Следует заметить, что интервал значений q ₀, допускающий бистабильность, должен также иметь и конечную нижнюю границу. Действительно, в модели Муни-Ривлина эластомер становится тем жёстче, чем сильнее он деформирован. Для близко расположенных частиц ( q ₀ >  2) даже малое абсолютное смещение означает заметную относительную деформацию и, следовательно, высокую энергию упругого отталкивания. Иными словами, если частицы находятся по соседству уже в исходном состоянии, то бистабильность не возникает из-за того, что паре «некуда» коллапсировать. Это и доказывает наличие конечной нижней границы q dn интервала начальных расстояний q ₀, внутри которого система проявляет бистабильность. В противоположность q ₀ ^up величина q ₀ ^dn должна убывать с ростом намагниченности насыщения ферромагнетика M_s и увеличением мягкости матрицы.

Уникальная особенность системы с насыщением намагниченности заключается в том, что при определённых условиях возникшая в ней бистабильность не приводит к образованию кластера. Пусть при некотором значении h ₀ вследствие изменения U_mag профиль энергии U ( h ₀, q , q ₀) превратился из одноямного в двухъямный, то есть появилась бистабильность. Если при этом значении h ₀

намагниченность близка к насыщению, то дальнейшее увеличение поля уже не влияет на U_mag , и значит, полная энергия U — см. (13) — становится независимой от величины поля. В такой ситуации бистабильность системы, обусловленная двухъямным профилем функции U ( q ), оказывается «латентной»: хотя её минимум энергии при q - 2 допускает переход в состояние кластера, однако осуществление его за счёт намагничивания системы невозможно.

Пример численного расчёта энергии U ( h ₀, q ) при заданном начальном размере пары приведён на рисунке 9; количественной характеристикой относительного влияния магнитных и упругих сил служит параметр

в = MS А- (14)

Рисунок 9 а показывает поведение пары в «мягком» материале ( в = 46). Как видно, в слабом поле имеется только один минимум энергии, соответствующий незначительному изменению исходного размера (кривая 1 ). С ростом величины поля возникает состояние с двумя минимумами (кривые 2 и 3 ), но затем первый минимум исчезает (кривая 4 ), и единственным устойчивым состоянием оказывается состояние кластера. Положение минимума и профиль энергии перестают меняться после того, как намагниченность частицы насыщается (кривые 4 и 5 ).

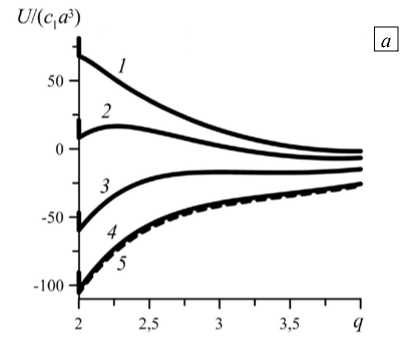
Рис. 9. Изменение профилей энергии взаимодействия частиц при q о = 4 для матриц разной жёсткости в : 46 ( а ) и 26 ( б ), и величине приложенного поля h ₀ : 1 (кривая 1 ), 2 ( 2 ), 3 ( 3 ), 4 ( 4 ) и 5 ( 5 ) (для различения кривых 4 и 5 последняя показана штрихами)

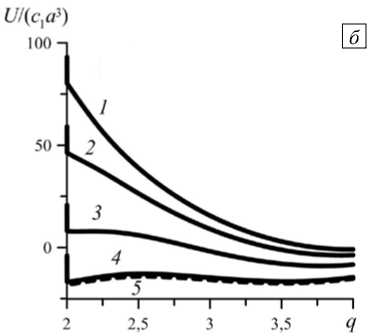
Иначе обстоит дело в системе с большей «жёсткостью» ( в = 26, Рис. 9 б ). В этом случае появившаяся бистабильность (кривая 3 ) сохраняется до значений поля, близких к отвечающим насыщению (кривая 4 ). В результате потенциал U ( q ) обладает двухъямным профилем в поле сколь угодно большой напряжённости (см. кривые 4 и 5 ). По этой причине магнитомеханический гистерезис оказывается «латентным»: состояние кластера возможно, но не реализуется. Если всё-таки в сильном поле кластер будет каким-либо образом создан, то при понижении величины поля он обязательно распадётся, и частицы разойдутся на исходное расстояние.

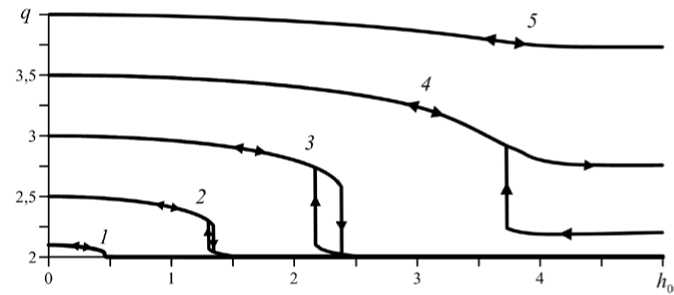
Рис. 10. Смещение частиц в зависимости от начального размера пары q ₀ : 2,1 (кривая 1 ); 2,5 ( 2 ); 3 ( 3 ); 3,5 ( 4 ); 4 ( 5 );

параметр в = 18

На рисунке 10 представлены деформационные отклики пар частиц в системе с фиксированным значением магнитомеханического параметра в . Для наглядности удобно полагать, что речь идёт о композиции полимер/ферромагнетик одного и того же состава, при этом пары частиц отличаются только своим начальным размером q ₀ . Проведённый выше качественный анализ позволяет легко разобраться в изображённых кривых. Так, кривая 1 показывает, что при очень близком расположении частиц альтернативные минимумы энергии почти совмещены, вследствие чего уплотнение пары до состояния кластера мало сказывается на её размере и происходит плавно. Магнитомеханический гистерезис существует явно в интервале 2,5 <  q 0 <  3,5 . На кривых 2 и 3 хорошо видны области бистабильности, ограниченные «ступеньками» (по q ), которые соответствуют: справа — входу в состояние кластера при увеличении поля; слева — выходу из этого состояния при снижении напряжённости поля.

Для пары частиц с начальным размером q 0 = 3,5 магнитомеханический гистерезис является «латентным» (кривая 4 ). Действительно, при любом увеличении / уменьшении величины поля размер пары меняется плавно, реализуется только верхняя ветвь кривой 4 . Наличие бистабильности (область двузначности кривой 4 ) означает, однако, что если двухчастичный кластер создастся посредством стороннего (немагнитного) воздействия, то система придёт к балансу магнитных и упругих сил, и этот объект станет устойчив во всей области, где существует нижняя ветвь кривой 4 . Для пар большого размера гистерезис невозможен (см. кривую 5 ), поскольку даже в состоянии насыщения магнитные силы много слабее упругих.

6.    Обсуждение результатов

Изучен механический отклик на приложенное однородное магнитное поле пары частиц изотропного ферромагнетика, заключённых в нелинейно-упругий эластомер. Главное внимание уделено случаю, когда межчастичные расстояния соизмеримы с размерами частиц. На этом масштабе в полной мере проявляются как особенности, связанные с неоднородностями локального поля, обусловленными взаимной магнитной индукцией частиц, так и нелинейность упругости полимера.

Рассмотренная задача важна для развития теории важного класса MR систем — мягких магнитных эластомеров (ММЭ). Из них наибольшую технологическую перспективу имеют ММЭ с высоким содержанием ферромагнитного наполнителя, то есть такие, где частицы находятся в близком (на расстояниях порядка их размера) соседстве. Именно указанная ситуация, хотя и в простейшем виде (для пары частиц), впервые изучена в настоящей работе. К тому же сближение двух частиц — это наиболее часто встречающийся тип концентрационной неоднородности в любых ММЭ. При этом пары близких частиц, как показывают модельные расчёты [20], имеют решающее влияние на магнитомеханику даже слабо концентрированных ММЭ.

Новизна представленного подхода состоит в том, что для расчёта магнитного взаимодействия частиц на малых расстояниях использован не парамагнитный (линейный), а реалистический (нелинейный) закон намагничивания ферромагнетика, учитывающий насыщение в сильном поле. Показано, что в этом случае задача аналитически не разрешима. В частности, межчастичная магнитная энергия не масштабируется в соответствии с величиной приложенного поля, в то время как для парамагнетиков существует универсальная зависимость « H 2 . Наблюдается также и значительная количественная разница с парамагнитным случаем обусловленная тем, что начальная магнитная восприимчивость ферромагнетика (железа) составляет 10 ³ - 10 ⁵ ед. СГСМ, в то время как у реальных (супер)парамагнетиков она на порядки ниже. Например, согласно [14], восприимчивость материала микросфер Dynabead равняется ~0,9б/ ( 4 п ) - 0,08 ед. СГСМ.

Разработанное описание силового взаимодействия ферромагнитных частиц использовано для изучения магнитомеханического гистерезиса пары частиц в полимерной матрице. Этот эффект был предсказан и исследован в работе [13] для парамагнитного случая. Как оказалось, для ферромагнетиков он также возможен, однако не всегда, а лишь в ограниченном диапазоне значений q ₀ — начального расстояния между частицами. Действительно, для ферромагнитных частиц абсолютным верхним пределом выигрыша по парной энергии магнитного взаимодействия является величина (4 л ² /9) M S a ³, которая соответствует плотному контакту частиц, построенных в конфигурацию «голова–хвост» и намагниченных до насыщения. В то же время упругая энергия при изменении межчастичного расстояния может расти фактически неограниченно.

Области существования магнитомеханического гистерезиса в модельном «двухчастичном» ММЭ (см. Рис. 8) представлены на рисунке 11 в координатах q ₀ и Р = M S Сс, , где параметр в определён формулой (14). Сплошная линия — это граница, выше которой гистерезисный переход в состояние кластера можно вызвать приложением внешнего поля. Между сплошной и штриховой линиями располагается область латентного гистерезиса, где для формирования кластера требуется сочетание

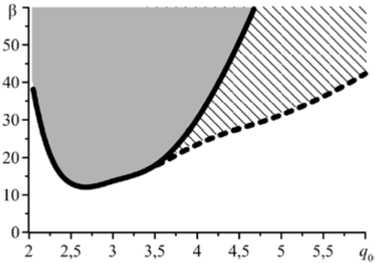
Рис. 11. Области существования магнитомеханического гистерезиса пары частиц ферромагнетика, заключённых в упругую матрицу и намагничиваемых в конфигурации «голова–хвост»; затемнённая область соответствует реализующемуся магнитомеханическому гистерезису, заштрихованная – латентному

намагничивания и некоторой сторонней (немагнитной) силы.

На рисунке 11 самая нижняя точка границы имеет координаты в - 11, q0 - 2,7. Ветви сплошной и штриховой границ, уходящие от неё направо вверх указывают, что чем выше намагниченность насыщения ферромагнетика (при заданной упругости матрицы), тем более удалённые частицы могут объединяться в кластер. Это может происходить либо за счёт магнитной силы как таковой (область над сплошной линией), либо при добавлении к магнитному притяжению некоторой сторонней, например, механической силы (область между сплошной и штриховой линиями). Следует отметить, что для линейно намагничивающихся частиц, рассмотренных в работе [13], величину Ms формально следует положить бесконечной. Таким образом, на рисунке 11 случаю линейного намагничивания соответствует бесконечно удалённая область в = ю; то есть для идеально парамагнитных частиц магнитный гистерезис существует всегда, при любых q0. Подъём границы в(qо) слева от точки минимума обусловлен нелинейностью модели Муни–Ривлина: с ростом относительной деформации жёсткость полимера увеличивается. По этой причине, чем ближе располагаются частицы в исходном состоянии, тем бóльшая магнитная сила требуется для того, чтобы они объединились в кластер.

Очевидно, что обсуждаемая двухчастичная модель не может претендовать на достоверное описание реального материала. Однако оценки, полученные с её помощью, интересны, поскольку дают представление о порядках величин, при которых следует ожидать мезоскопического гистерезисного отклика ММЭ. Это тем более важно, что макроскопическими следствиями кластерообразования должны быть, в частности, наблюдаемые в эксперименте рост модуля упругости и возникновение индуцированной пластичности.

Характерное значение параметра в в нижней точке диаграммы на рисунке 11 составляет в* ~ MSccx ~10. Подстановка в это выражение значения Ms2 ~ 3 х106 ед.СГСМ2 (для железа) и учёт того, что коэффициенты c1,2 потенциала Муни–Ривлина (10) связаны с начальным модулем Юнга E матрицы соотношением E = 6c 1 (1 + c2) [18], дают E. ~2х106дин/см2 = 200 кПа . Как вытекает из определения в , оценка E. есть максимальное значение модуля, при котором возможен магнитомеханический гистерезис.

У типичных ММЭ модуль Юнга E _exp , найденный экспериментально, лежит в диапазоне 30-100 кПа [21, 22], то есть для таких эластомеров выполняется соотношение E exp <  E , . Кроме того, следует учесть, что рассматриваемый магнитомеханический гистерезис — это результат решения мезоскопической задачи, так что величина E (или с 1 ), входящая в выражение для в , имеет смысл модуля Юнга самой полимерной матрицы, а не модуля композита в целом. Чтобы произвести оценку E , соответствующего заданному E _exp , можно обратиться к резиноподобному эластомеру, наполненному химически инертными твёрдыми сферическими микрочастицами. При объёмной концентрации частиц около 25–30% соотношение между макроскопическим модулем E _exp такой системы и модулем Юнга матрицы составляет E exp ~ 3 E [23]. Отсюда следует, что для указанных выше значений E exp величина E находится в интервале 10-30 кПа, то есть условие E <  E . ~ 200 кПа оказывается выполненным с большим запасом. Таким образом, по крайней мере, согласно критерию, следующему из модели парного взаимодействия частиц, в реальном композите выполняются все необходимые условия для реализации магнитомеханического гистерезиса.

Опираясь на результаты вычислений, можно предложить следующую качественную картину намагничивания образца ММЭ. Наложение внешнего однородного магнитного поля вызывает массовое объединение двух- (а, возможно, и многочастичных) кластеров из частиц, которые по статистическим причинам оказались наиболее близко отстоящими друг от друга. Такие агрегаты принимают на себя роль «магнитных скрепок» [24, 25]: они создают и поддерживают внутренние напряжения в композите до тех пор, пока поле не будет выключено. Именно образованием таких «скрепок» и вызван рост упругого модуля и переход ММЭ к пластичности [21]. Свой вклад в структурирование вносит и «латентный» гистерезис. Как показано выше, этот механизм агрегирования не может проявиться, если образец свободен от внешних нагрузок. Однако любой эксперимент по измерению механических свойств подразумевает деформацию образца. Нагрузки, сопровождающие деформацию, способны превратить потенциальный (латентный) гистерезис в реальный, то есть вызвать формирование добавочных кластеров. Согласно рисунку 11, учёт латентного гистерезиса значительно расширяет диапазон материальных параметров, в котором возможна кластеризация. Все эти соображения дают основание полагать, что магнитомеханический гистерезис является одним из главных, а возможно, и единственным путём кластеризации реальных ММЭ, произведённых на основе микрочастиц железа.

7.    Выводы

Изучено магнитостатическое (пондеромоторное) взаимодействие, возникающее между двумя частицами изотропного ферромагнетика, помещёнными во внешнее поле. Показано, к каким отличиям в межчастичных силах — по сравнению со случаем (супер)парамагнетика — приводит эффект насыщения намагниченности.

Установлено, что для пары ферромагнитных частиц, помещённых в эластомерную матрицу, как и для (супер)парамагнитных частиц в тех же условиях, возможно образование кластера по сценарию магнитомеханического гистерезиса. Однако из-за насыщения намагниченности эффект существенно отличается от парамагнитного случая. Во-первых, бистабильность системы и её гистерезис наблюдаются только в ограниченной области значений материальных параметров системы. Во-вторых, наряду с гистерезисом, возникающим только под воздействием поля, осуществим также и «латентный» гистерезис, для реализации которого требуется дополнительный фактор, например, приложение извне механических напряжений и/или деформаций.

Полученное решение задачи взаимодействия двух ферромагнитных частиц использовано для оценки возможностей кластерообразования в ансамблях микрочастиц железа, которыми наполнены реальные магнитореологические эластомеры. Обоснована важная роль гистерезисного механизма в изменении структуры этих композиционных материалов.

Работа выполнена при финансовой поддержке Комплексной программы Президиума УрО РАН (проект № 15-10-1-18), РФФИ (проект № 13-01-96056) и Министерства образования и науки Пермского края (соглашение № С-26/617).