Бистабильный осциллятор Дюффинга в дискретном времени

Осциллятор Дюффинга, наряду с осциллятором ван дер Поля, является, пожалуй, наиболее известной моделью теории нелинейных колебаний. Он введен в рассмотрение при исследованиях колебаний механических систем с кубически-нелинейной жесткостью пружины [1; 2]. В безразмерных переменных осциллятор представляет уравнение Дюффинга d ² x    dx

—- + 5— + х + х ³ = E cos( to _c t ),                     (1)

dt2 dt                     s где 5 - константа линейной диссипации; E и tos - амплитуда и частота внешнего воздействия. Уравнение (1) широко используется также при описании явления нелинейного резонанса в радиотехнике [3] и других физических приложениях [4].

Линейная жесткость в (1) положительна. В отличие от этого, в работе [5] (см. также [6; 7]) рассмотрена бистабильная магнитоупругая система (упругая балка в поле двух постоянных магнитов) с отрицательной линейной жесткостью, в которой колебания моделируются уравнением Дюффинга вида x-+- + 5—-х + х3 = E cos(to_ t).                     (2)

dt ^{2 dt                      s}

В отсутствие внешнего воздействия система (2) релаксирует к одному из двух состояний равновесия: X± = ±1. Результаты численного интегрирования уравнения (2) демонстрируют наличие в системе режимов вынужденных колебаний с хао- тическими переходами между окрестностями X±. Таким образом, «мягкий» осциллятор Дюффинга в форме (2) представляет интерес для численных экспериментов с бистабильными системами, в том числе для исследований индуцированных шумом переходов [8] и стохастического резонанса [9]. При этом такие исследования имеет смысл проводить с использованием образов осциллятора в дискретном времени – дискретных отображений осциллятора.

В статье [10] дискретное отображение осциллятора Дюффинга с положительной жесткостью (1) получено на основе принципа сохранения в процессе временной дискретизации импульсного отклика линейной системы-прототипа. В настоящем сообщении такой подход применен для построения дискретного отображения осциллятора с отрицательной жесткостью («мягкого» осциллятора).

1.    Физически обоснованная дискретизация времени

В качестве порождающего движения рассмотрим собственные осцилляции системы (2) в окрестностях состояний равновесия X± . Они описываются однородным линеаризованным уравнением d2 x + dt2

to, dx о

-r+to O - = 0, Q dt

где tog = 7ЗX2 -1 и Q = tog / 5 - частота и доброт- ность осцилляций.

Уравнение (2) с учетом (3) преобразуем к виду

d ² x    to dx 2            x                 X

+ 0 -— + to Q x = to Q G ( x ) + to Q E cos( to st ).            (4)

d_t ²    Q dt

Здесь нелинейная функция

G( x ) = 2

x ,

а для амплитуды внешнего воздействия оставлено прежнее обозначение. Предполагая в дальнейшем переход к дискретному времени с интервалом дискретизации А, введем в уравнение (4) безразмерную временную переменную т = t / А и запишем его в виде

б

d ² x _о О₀ dx --+ 2п ⁰—

+ 4 n ² o Q x =

d т ² Q d т

= 4 n ² o Q G ( x ) + 4 л ² П 2 E cos ( 2 nQ s т ) .

Здесь Q _q = ® ₀ / to d - собственная частота, измеряемая в единицах частоты дискретизации to d = 2 п / А , а = exp( -nO g / Q ) - параметр линейной диссипации.

Теперь уравнение движения (6) имеет вид, стандартный для осциллятора с нелинейной реактивностью, и метод статьи [10], основанный на использовании функции Грина уравнения (3), при-

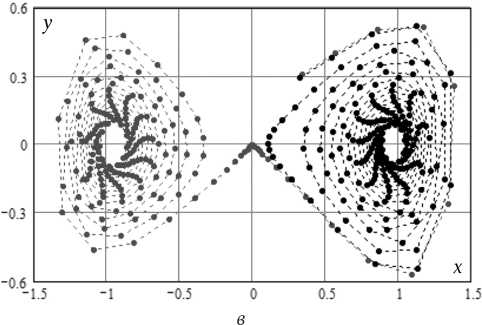
Рис. 1. Фазовые плоскости ДОД

Fig. 1. Phase planes of discrete Duffing oscillator

водит к разностному уравнению для дискретных отсчетов xn = x(тn) осцилляций xn - 2а cos (2nQ0 ) xn-1 +а2xn-2 =

= 1 G(xn-1) +1E cos cos (2nQs (n -1)), где параметр 1 = 2nQgа sin (2nQg).

Динамическую систему, функционирующую в дискретном времени в соответствии с уравнением движения (7), в дальнейшем будем обозначать как дискретный осциллятор Дюффинга (ДОД), указывая при необходимости на отрицательную жесткость прототипа в непрерывном времени. Пользуясь терминологией нелинейной динамики, можно говорить также о дискретном отображении осциллятора Дюффинга.

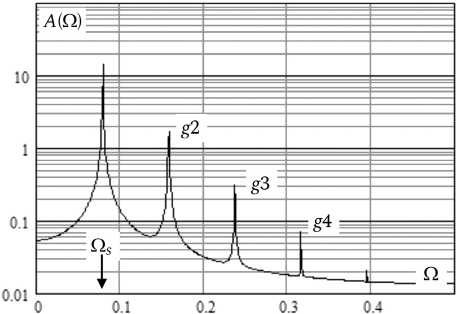
Рис. 2. Амплитудный спектр колебаний типа 1

Fig. 2. The amplitude spectrum of the oscillations of type 1

2.    Регулярная динамика ДОД

Нетрудно показать, что в автономном режиме уравнение (7), помимо неустойчивого X q = 0, допускает два устойчивых стационарных решения (для них сохранены прежние обозначения):

X _± = ± ^3 - 2 1^{- 1} ( 1 - 2 а cos(2 nQ _g) + а ² ) .           (8)

Они незначительно отличаются от значений

X ± = ± 1, наблюдаемых в осцилляторе (2). Напри-

б

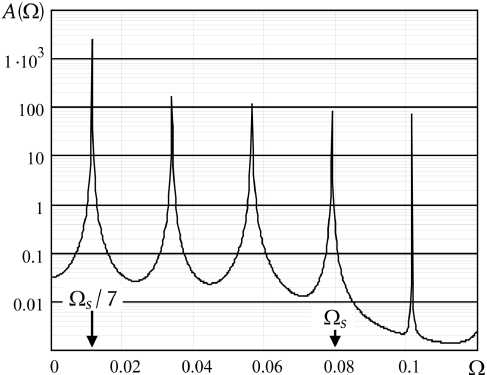
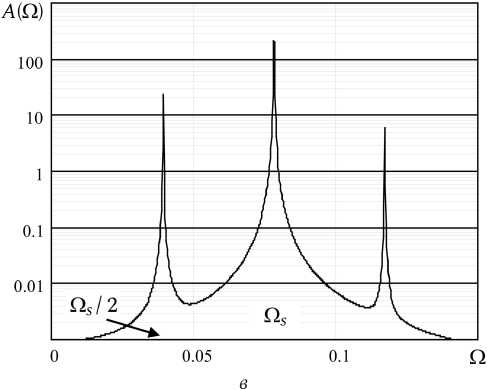
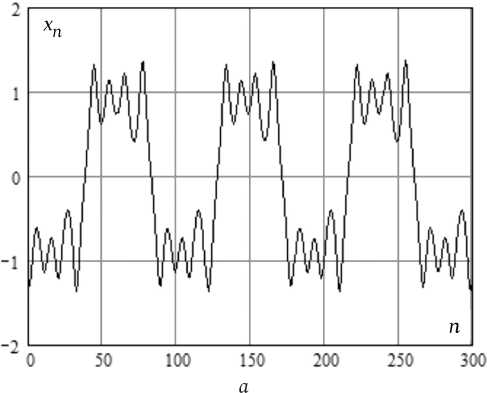
Рис. 4. Реализация ( а ), траектория ( б ) и амплитудный спектр ( в ) колебаний с удвоением периода

Fig. 4. Realization ( a ), trajectory ( b ) and amplitude spectrum ( c ) of oscillations with doubling the period

в

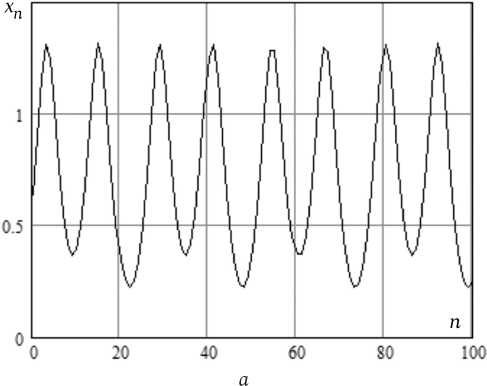
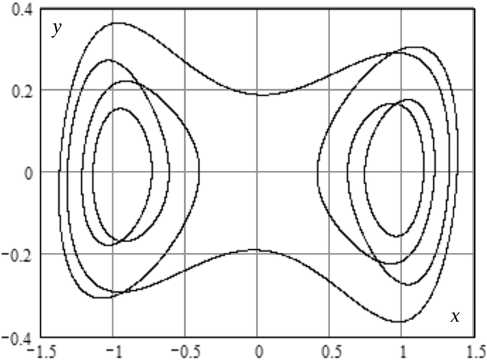
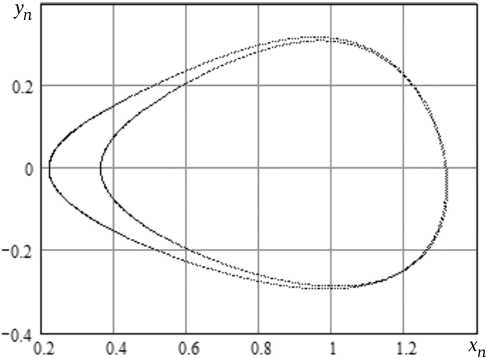
Рис. 3. Реализация ( а ), траектория ( б ) и амплитудный спектр ( в ) колебаний типа 2

Fig. 3. Realization (a), trajectory (b) and amplitude spectrum (c) of type 2 oscillations мер, при Q0 = 0,1 и Q = 30 X±=±0,965. При переходе к непрерывному времени, т. е. при Qo ^ 0, X± ^±1. Таким образом, в рамках предложенного способа дискретизации времени стационарные состояния осциллятора испытывают лишь слабые возмущения.

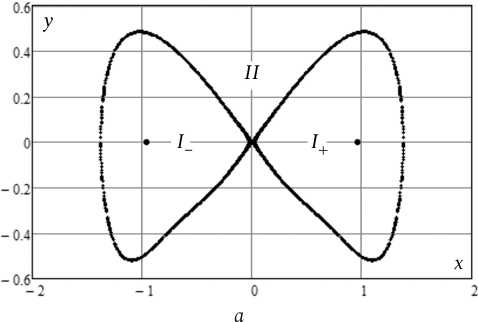
На рис. 1, а на фазовой плоскости ДОД показаны состояния X _± = ± 0, 965 и гомоклиническая орбита состояния X о = 0. Гомоклиническая орбита делит

а

в

Рис. 5. Характеристики хаотических колебаний

Fig. 5. Characteristics of chaotic oscillations фазовую плоскость на области I -, I + и II. Траектории консервативного осциллятора (Q ^ го) на рис. 1, б в зависимости от начальных условий либо локализованы в областях I - или I + (локальные осцилляции 1 в окрестностях стационарных состояний), либо принадлежат области II (глобальные осцилляции 2 между состояниями X±).

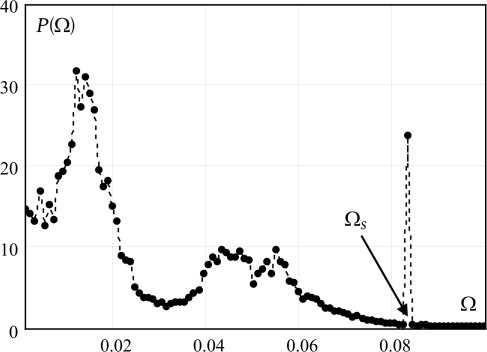
Рис. 6. Спектр мощности хаотических колебаний

Fig. 6. Power spectrum of chaotic oscillations

Наличие диссипации приводит систему в одно из устойчивых состояний (рис. 1, в ).

В режиме внешнего воздействия ДОД (7) демонстрирует различные варианты ангармонических колебаний. В частности, траектории области 1 – это простейшие нелинейные осцилляции со спектром, обогащенным гармониками, как это следует из рис. 2, на котором представлен амплитудный спектр A( Q ) вынужденных колебаний ДОД с параметрами Q _o = 0,1, Q = 30, Q _s = 0,079, E = 0,05.

При увеличении амплитуды внешнего воздействия до значения E = 0,07 в осцилляторе наблюдаются вынужденные колебания, имеющие траекторию в области 2, показанную на рис. 3, б . Отрезок их реализации изображен на рис. 3, а . Амплитудный спектр на рис. 3, в указывает на то, что основным типом движения здесь являются субгармонические колебания с частотой Q _s /7, составляющей одну седьмую часть частоты внешнего воздействия. В окрестностях потенциальных ям они сопровождаются более высокочастотными колебаниями с траекториями области 1 с частотой, близкой к частоте Q o .

Переход к траекториям в области 2 в ряде случаев сопровождается бифуркациями удвоения периода траекторий в области 1. Рис. 4 иллюстрирует этот эффект для системы с параметрами Q o = 0,1, Q = 30, Q _s = 0,078, 0,07. С ростом амплитуды внешнего воздействия Е серия повторных бифуркаций приводит к переходу от периодического движения к хаотическому.

3.    Хаотическая динамика ДОД

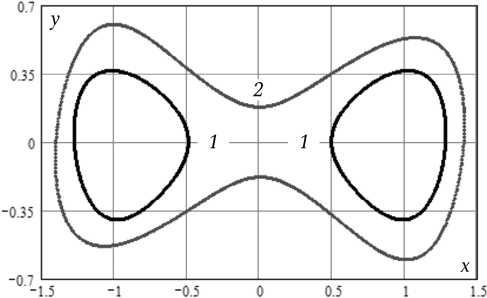
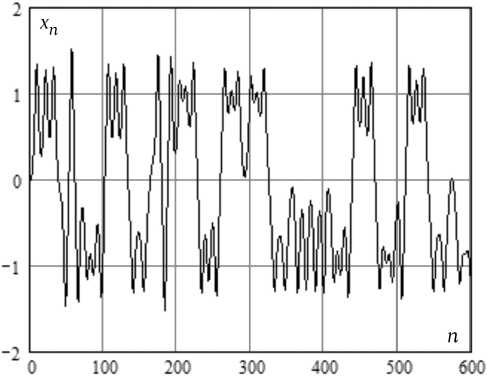
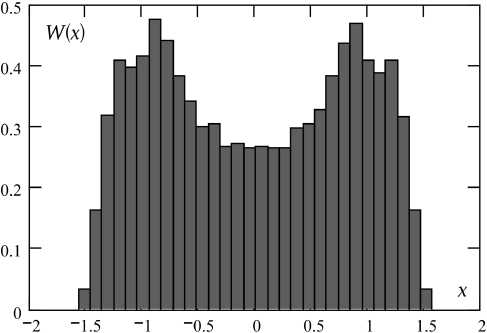
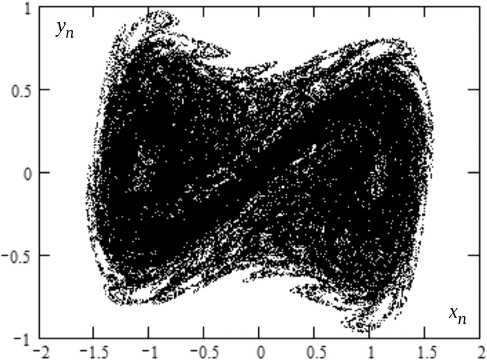
Пример типичной реализации хаотических колебаний дан на рис. 5, а для осциллятора с параметрами Qo = 0,1, Q = 30, Qs = 0,0833, E = 0,11. Гистограммная оценка плотности вероятности процесса xn приведена на рис. 5, б, и фазовый портрет колебаний – на рис. 5, в.

Визуально реализация процесса указывает на его нерегулярность: осцилляции в окрестностях состояний X ± сопровождаются хаотическими переходами между ними. Фрактальная структура хаотического аттрактора на рис. 5, в характеризуется значением корреляционного показателя v = 1,88 ± 0,01.

На рис. 6 приведена периодограммная оценка спектра мощности процесса x_n . Как видно из графика, спектр содержит дискретную линию на частоте внешнего воздействия Q _s = 0,08333 и сплошную компоненту. Наличие сплошной части спектра является еще одним эвристическим критерием динамического хаоса [11].

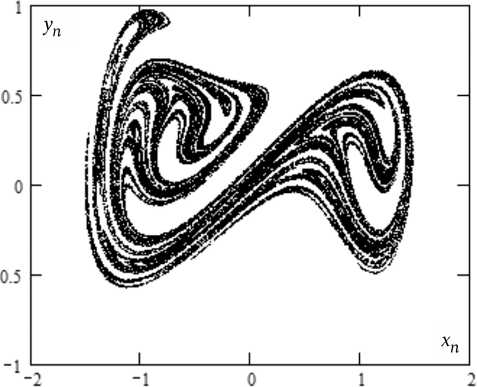
Рис. 7. Отображение Пуанкаре ДОД

Fig. 7. Poincare mapping of discrete Duffing oscillator

4.    Отображение Пуанкаре хаотических колебаний ДОД

Для режима хаотических колебаний, помимо аттрактора на рис. 5, в, приведем также отображение Пуанкаре осцилляций. Введя фазовую переменную 0n, ДОД (7) представим в виде автономной системы xn - 2а cos (2nQ0) xn-1 + а2 xn-2 = = X G( xn-1) + X E cos( 0 n-1), 4nQ0Уп = 3xn - 4xn-1 + xn-1, 0n =0n-1 + 2nQ$ .

Отображения Пуанкаре формируются в сечениях трехмерного пространства (x, y, о) динамической системы (9) плоскостями 0n : mod(2n) = const. На рис. 7 представлено сечение Пуанкаре ДОД с параметрами Q0 = 0,1, Q = 30, Q s = 0,0833,

E = 0,11, плоскостью 0 n : mod(2 n ) = 2 n / 3. Корреляционный показатель для этого отображения имеет значение v = 1,72 ± 0,01.

Визуально и по значению корреляционного показателя представленное здесь отображение Пуанкаре соответствует приведенным в [6].

Заключение

Введенный в рассмотрение вариант осциллятора Дюффинга с мягкой восстанавливающей силой, функционирующий в дискретном времени, - «мягкий» дискретный осциллятор Дюффинга - предлагается использовать для исследования физических явлений в бистабильных колебательных системах, находящихся под действием детерминированных и случайных сигналов. В режиме генерации динамического хаоса бистабильный ДОД может служить источником псевдослучайных сигналов.