Блочно-ориентированные модели

Введение . Автоматизация и развитие производства, на сегодняшний день, немыслимы без использования многообразия методов построения адекватных математических моделей объектов для целей управления. Современные системы управления разрабатываются, в наибольшей степени, для сложных многоэлементных производств, при описании которых, получаются довольно сложные модели. Если, не брать во внимание внутреннюю структуру исследуемого объекта, а моделировать связь между его входным и выходным процессами, мы получим значительное упрощение модели. Идентификация – формирование математической модели динамической системы на основе результатов обработки, регистрируемых входных и выходных сигналов [1].

Наиболее широко разрабатываемым подходом в области идентификации нелинейных объектов является описание предметов при помощи блочно-ориентированных моделей [2, 3]. Данные модели используются при моделировании непростых экономических предметов [4], в области энергетики [5], нефтегазовой промышленности [6] и на прочих непростых технических предметах.

Объектом проведения исследования есть нелинейный управляемый одномерный динамический предмет с вымеряемыми в дискретные моменты времени выходом y(t) и входом u(t) (рисунок 1).

Рисунок 1 – Структура объекта идентификации

Свойства нелинейности и динамики подобных пред- метов в ряде случаев нельзя отчетливо поделить. И чтобы упростить задачу изучаемый нелинейный динамический предмет выставляют в облике отдельной комбинации линейных динамических блоков и безынерционных нелинейных блоков [7]. Данный подход к моделям даёт возможность связать входные и выводные переменные предметов с разнообразным строением и уровнем нелинейности. К подобным системам относят системы типа Гаммерштей-на [8], Винера, Винера-Гаммерштейна [9, 10], фильтра Заде [11, 12], обобщенной модели Винера.

Идентификация систем основывается в основном на линейных стационарных моделях, которые широко применяются для производственных процессов. В то же время большинство реальных систем являются нелинейными и обладают, с точки зрения организации процесса управления, многими "неудобными" свойствами. Представление таких систем линейными стационарными моделями не дает приемлемых для практики результатов. Рассмотрим наиболее подробно классы моделей и входных сигналов.

Определение строения модели реализовывается из надлежащего класса непрерывных блочно-ориентированных моделей [13]:

L={si│i=1,2,3,…,10} где s1 – нелинейная статическая модель, s2 и s3 – легкая и обобщенная модели Гаммерштейна, s4 и s5 – легкая и обобщенная модели Винера, s6 – легкая каскадная модель Винера-Гаммерштейна, s7 – расширенная модель Винера, s8 и s9 – легкая и обобщенная каскадные модели Винера-Гаммерштейна, s10 – модель фильтра Заде.

Обозначим u(t) и y(t) – выходная и входная переменные, соответствующе. Нелинейные статистические элементы, входящие в состав моделей, очерчиваются полиномиаль- ными функциями второй степени:

f₁ [ x(t) ] =c₀+c₁ x(t)+c₂ x²(t)

f₂ [ x(t) ] =d₀+d₁ x(t)+d₂ x²(t)

c_i, d_i (i=0,1,2) – постоянные коэффициенты, W(p), W_i(p) (i=1,2,3,4) – передаточные функции линейных динамических систем в оперативной форме, т.е. p означает инерцию дифференцирования: p≡d/dt .

Подразумевается, что линейные динамические звенья, входящие в состав класса блочно-ориентированных моделей, устойчивы, т.е. корни их характеристических уравнений расположены в левой полуплоскости плоскости корней.

Рассмотрим наиболее подробно основные модели L и их уравнения. Одной из них является простая модель Гаммерштейна. Она применяется в случае, когда постоянная составляющая выходного периодического сигнала не зависит от изменения частоты входного воздействия (рисунок 2).

y(t)=c0 W(0)+c1W(p)u(t)+c2W(p)u2(t)

В ситуации, когда разность между постоянной составляющей и амплитудой второй гармоники зависит от частоты, применяется простая каскадная модель Винера-Гаммер-штейна (рисунок 6).

y(t)=c0W(0)+c1W1(p)W2(p)u(t)+c2W2(p)[W1(p)u(t)]2

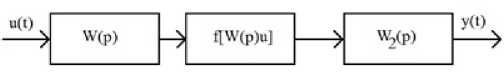
Рисунок 6 – Простая каскадная модель Винера-Гаммерштейна

Когда все перечисленные выше величины зависят от частоты, однако постоянная составляющая и отношение разности постоянных составляющих при разных амплитудах входного воздействия к амплитуде второй гармоники, представляют собой тригонометрические функции от частоты, применяется расширенная модель Винера (рисунок 7).

y(t)=c₀+c₁W₁(p)u(t)+ [ W₂(p)u(t) ][ W₃(p)u(t) ]

u(t)

^ f(u)

} W(p)

y(D

Рисунок 2 – Простая модель Гаммерштейна

В случае, когда постоянная составляющая выходного сигнала не имеет зависимость от изменения частоты входного воздействия, применяется обобщенная модель Гаммерштейна. Она имеет различие от простой модели Гаммерштейна по структурным особенностям модели (рисунок 3).

y(t)=c0+W1(p)u(t)+W2(p)u2(t)

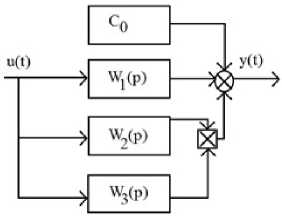
Рисунок 7 – Расширенная модель Винера

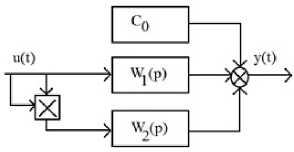
Рисунок 3 – Обобщенная модель Гаммерштейна

В ситуации, когда постоянная составляющая и отношение разности постоянных составляющих при разных амплитудах входного воздействия к амплитуде второй гармоники, зависят от частоты, однако эти зависимости не являются тригонометрическими функциями от частоты, применяется Обобщенная каскадная модель Винера-Гаммерштейна (рисунок 8).

y(t)=c₀+c₁W₁(p)u(t)+W₃(p) [ W₂(p)u(t) ] ²

В ситуации, когда постоянная составляющая выходного периодического сигнала зависит от изменения частоты входного воздействия, применяется простая модель Винера. Отношение амплитуды первой гармоники к амплитуде второй гармоники и разность между постоянной составляющей и амплитудой второй гармоники не зависят от частоты (рисунок 4).

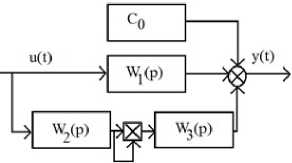
Рисунок 8 – Обобщенная каскадная модель Винера-Гаммерштейна

y(t)=c₀+c₁W(p)u(t)+c₂ [ W(p)u(t) ] ²

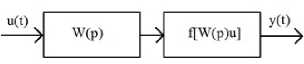
Рисунок 4 – Простая модель Винера

В случае, когда разность между постоянной составляющей и амплитудой второй гармоники не зависит от частоты, а отношение квадрата амплитуды первой гармоники к амплитуде второй гармоники зависит от частоты, применяется обобщенная модель Винера (рисунок 5).

В случае, когда постоянная составляющая представляет собой тригонометрическую функцию от частоты, однако отношение разности постоянных составляющих при разных амплитудах входного воздействия к амплитуде второй гармоники зависит от частоты, однако эта зависимость не является тригонометрической функцией от частоты, применяется Расширенная каскадная модель Винера-Гаммерштейна (рисунок 9).

y(t)=c₀+c₁W₁(p)u(t)+W₄(p) {[ W₂(p)u(t) ][ W₃(p)u(t) ]}

y(t)=c₀+c₁ W₁(p)u(t)+c₂ [ W₂(p)u(t) ] ²

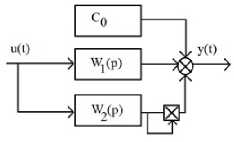
Рисунок 5 – Обобщенная модель Винера

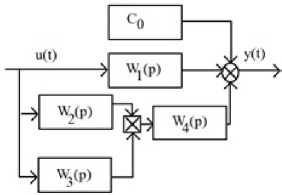
Рисунок 9 – Расширенная каскадная модель Винера-Гаммерштейна

В ситуации, когда выходной периодический сигнал содержит третью и четвертую гармонику применяется Простая каскадная модель Гаммерштейна-Винера (рисунок 10).

y(t)=d0+c0d1W(0)+c02d2W2(0)

+ [ c₁d₁W(p)+2c₀c₁d₂W(0)W(p) ] u(t)

+ [ c₂d₁W(p)+c₁²d₂W²(p)+2c₀c₂d₂W(0)W(p) ] u²(t)

+2c1c2d2W2(p)u3(t)+c22d2W2(p)u4(t)

Рисунок 10 – Простая каскадная модель Гаммерштейна-Винера

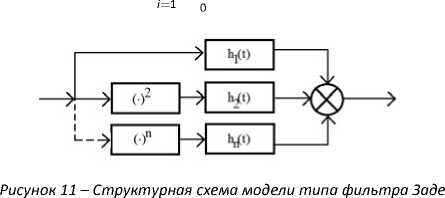
В случае, когда постоянная составляющая выходного периодического сигнала не зависит от степени нелинейного преобразования, применяется Модель фильтра Заде (рисунок 11).

y (t ) = y о + £ a i J h ( q ) x¹ ( t - q ) d q + g (t )

Таким образом, по фазовому сдвигу выходных вынужденных колебаний системы относительно входного сигнала и по зависимости постоянной составляющей этих колебаний, которую можно определить с помощью численного гармонического анализа, от периода входного сигнала, структуру модели исследуемой системы можно отнести к определенному подмножеству множества моделей.

Идентификация систем связана с решением разных задач в зависимости от априорной информации о системе. Построение оптимальной модели системы во многом определяется решением задачи структурной идентификации. Рассмотрим наиболее подробно программное обеспечение идентификации для класса блочно-ориентированных моделей.

Задача идентификации нелинейных динамических моделей в классе блочно-ориентированных моделей является принципиально более сложной и объемной задачей в данной научной области. Решение данного класса задач требует использования специализированных программных средств.

На сегодняшний день в связи с быстрым развитием информационных технологий IT рынок предлагает пользователям обширный список программных продуктов для работы с математическими моделями [14]. Самой функциональной программной системой для решения задач как технических вычислений, так компьютерного моделирования является MATLAB.

Для реализации компьютерного моделирования в MATLAB используется дополнительно ПО Simulink, который требуется для любого проектирования и моделирования в среде MATLAB и тесно интегрируется в нее, не являясь самостоятельным ПО. Является расширяемым программным обеспечением за счет использования библиотек готовых блоков. Позволяет работать с различными видами линейных и нелинейных объектов. Библиотека источников сигнала реализует генерацию сигнала, подаваемого на вход модели, а средствами самой MATLAB возможна статистическая обработка результатов моделирования.

Для решения задач идентификации в состав среды MATLAB входит пакет System Identification Toolbox [15]. Пакет System Identification Toolbox в своем составе содержит средства для создания математических моделей нелинейных динамических объектов, на основе наблюдаемых вход-ных/выходных данных. Он поддерживает работу со следующими нелинейными моделями:

— ARX

Рисунок 12 – Структурная схема нелинейной ARM модели

— Гаммерштейна-Винера (простая модель Гаммерштей-на, простая модель Винера, простая каскадная модель Гам-мерштейна-Винера)

Рисунок 13 – Структурная схема модели Гаммерштейна-Винера

Получив модели с найденными параметрами, их можно импортировать в MATLAB/Simulink для построения схем более сложных моделей. На рисунках 14-16 приведены схемы Simulink-модели для нелинейных моделей Винера и Гам-мерштейна [16].

Рисунок 14 – Simulink-схема нелинейной модели Винера

Рисунок 15 – Simulink-схема нелинейной модели Гаммерштейна

Рисунок 16 – Simulink-схема нелинейной модифицированной модели Гаммерштейна

Заключение . Блочно-ориентированные модели широко используются при решении задач по идентификации динамических объектов. Данные модели не ограничиваются какой-то лишь одной сферой применения, они присутствуют во всех сферах деятельности человека. Применение таких моделей, для примера, начинается на этапах разработки сложных аппаратов, ракет, кораблей и может заканчиваться информационными сетями.

В работе критерий определения структуры модели разработан на основе использования численного гармонического анализа. Класс входных периодических сигналов, имеющих равномерно и абсолютно сходящие ряды Фурье, включает в себя такие сигналы, как симметричный треугольный импульс, симметричный трапецеидальный импульс, полусинусоидальный импульс и др. Численный гармонический анализ полученных на выходе вынужденных колебаний, позволяет выделить определенные подмножества множества моделей для представления структуры модели исследуемой нелинейных систем. Определение структуры модели входных синусоидальных воздействиях.