Блуждания зеркально отражающего погруженного диска в подогреваемом падающим излучением конвективном слое

С момента зарождения науки о низкоразмерном хаосе популярными в этой области объектами исследований являются конвективные системы [1, 2] . На первых порах внимание в основном привлекали конвективные течения при слабой надкритичности, когда возбуждается лишь несколько мод, то постепенно стало ясно, что низкоразмерный хаос может возникать и на фоне развитой конвективной турбулентности [3, 4] . При наличии в потоке крупномасштабных свободно плавающих тел, влияющих на тепло- и массообмен в жидкости и переносимых этой жидкостью, поведение системы в целом еще больше усложняется. В основном системы такого рода рассматриваются в контексте гео- и астрофизических приложений, например, в задачах о плавающих континентах [5] , облачных кластерах [6] , активных областях в звездных конвективных оболочках [7] .

Поведение подобных сложных систем, помимо традиционных для конвекции управляющих параметров, зависит от геометрии полости и формы плавающего тела, соотношения теплофизических свойств жидкости и тела, граничных условий на стенках полости и на самом теле. Необходимы простые, пусть и академические, задачи, позволяющие выявить основные закономерности в их динамике. Первой задачей такого рода стало изучение одномерных движений теплоизолирующей пластины, свободно плавающей на поверхности жидкости в ячейке Рэлея–Бенара, предпринятое в контексте моделирования динамики тектонической плиты, подверженной влиянию конвекции в мантии [8] . Серия экспериментальных и численных исследований показала, что движение плиты характеризуется сложной динамикой, которая зависит от размера пластины и числа Рэлея [9, 10] .

Задача с погруженным теплоизолирующим телом впервые рассмотрена в работе [11] , в которой экспериментально изучалась динамика круглого диска, плавающего на заданной глубине в вытянутой прямоугольной кювете с твердыми горизонтальными теплообменниками, фиксирующими температуру на нижней и верхней границах слоя. Было показано, что для выбранной ячейки шириной чуть больше диаметра диска и длиной около двух диаметров поведение диска определяется двумя управляющими параметрами: числом Рэлея, которое отвечает за интенсивность конвекции в слое, и относительной глубиной погружения диска. На плоскости этих параметров была построена карта режимов, включающая область покоя диска, область его регулярного периодического движения из одного крайнего положения в другое и область хаотических одномерных движений. Лабораторные и вычислительные эксперименты, выполненные для разных геометрий ячейки и глубин погружения диска, показали, что периодические режимы возникают, если диск плавает вблизи теплового пограничного слоя, причем эти режимы возможны в ограниченном диапазоне значений как чисел Рэлея, так и аспектного отношения, определяющего длину полости в единицах диаметра диска [12] .

Двумерные блуждания диска в протяженном, квадратном в плане, подогреваемом снизу слое жидкости со свободной верхней поверхностью исследовались экспериментально в работе [13] . Было продемонстрировано, что динамика диска в основном определяется крупномасштабными модами: тороидальным вихрем с нисходящей жидкостью в центре и крупномасштабными вихрями вдоль каждой из координат, существующими на фоне интенсивных, но относительно короткоживущих мелкомасштабных конвективных ячеек. Над блуждающим

Статья опубликована в открытом доступе по лицензии CC BY 4.0

диском образуется холодное пятно, которое влияет на крупномасштабную циркуляцию, но слабо сказывается на конвективных ячейках масштаба толщины слоя, которые обеспечивают основной перенос тепла и доминируют в верхней части слоя. Несмотря на существенно трехмерную структуру течения, которая принципиально отличается от конвективного течения в вытянутом резервуаре с одномерными движениями диска, перемещения по каждой координате выглядят аналогично одномерным движениям.

В контексте задач о движении облачных кластеров интересным становится радиационный нагрев подстилающей поверхности с учетом оптических свойств плавающего тела. Эксперимент с одномерными движениями диска в радиационно подогреваемом слое показал, что зеркально отражающий диск может совершать периодические движения, в то время как поглощающий или отражающий свет диск прижимается к боковой стенке и остается там [14] . Этот факт подтвержден численным моделированием в работе [15] , где также исследованы перемещения диска и тепломассопернос в конвективном слое при наличии в нем диска с частично отражающей и частично пропускающей свет поверхностью.

В данной работе рассматриваются двумерные блуждания диска в протяженном слое жидкости, подогреваемом падающим сверху потоком излучения. Основной упор сделан на вычислительные эксперименты, которые позволили не только проследить за движениями диска, но и показать полную трехмерную структуру конвективного течения, а также выяснить роль степени однородности распределения радиационного нагрева по подстилающей поверхности. Выполнены верификационные лабораторные эксперименты, подтвердившие адекватность численных расчетов и прояснившие роль оптических свойств плавающего тела.

2. Постановка задачи

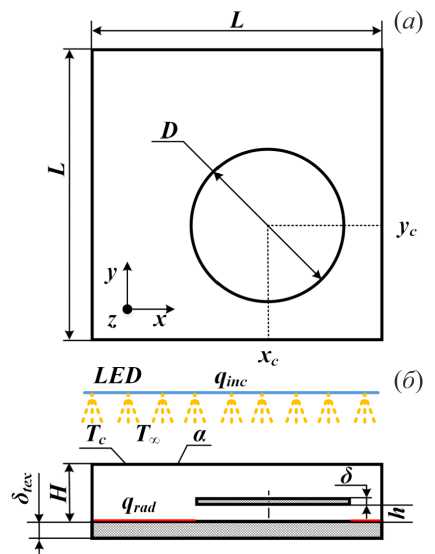
Рис. 1. Схема к постановке задачи: вид кюветы сверху ( а ) и спереди ( б )

Рассматриваются движения свободно плавающего, но погруженного на фиксированную глубину, твердого тела (диска) в слое жидкости над нагреваемой излучением поверхностью (Рис. 1) . Рабочей жидкостью служит вода, налитая в кювету квадратного сечения, над которой расположен источник света такой же площади в виде набора светодиодных лент (LED). Дно кюветы представляет собой текстолитовую пластину, покрытую светопоглощающей краской. Верхняя граница кюветы открыта. В воде на расстоянии h от дна помещен способный свободно плавать в горизонтальной плоскости диск с зеркальной верхней поверхностью. Источник LED излучает свет в видимом диапазоне, для которого вода является прозрачной средой, под диском же образуется тень, вне которой закрашенное дно кюветы нагревается. Конвективные потоки, которые формируются в кювете, передвигают диск вместе с теневой областью. Установка имеет следующие размеры: сторона кюветы L = 258 мм, уровень воды H = 30 мм, толщина пластины из текстолита δ _tex = 10 мм, толщина диска δ = 2 мм, расстояние нижней стороны диска от поверхности текстолита h = 3 мм. Диаметр диска D = 123 мм.

Задача решается методами вычислительной гидродинамики на основе системы уравнений свободной конвекции несжимаемой жидкости в приближении Обербека–Буссинеска, уравнения движения диска и уравнения

теплопроводности для пластины из текстолита и диска:

— + ( u -V ) u —--- + ^v V 2 u - g ^e (T ^- T o ),

∂t               ρ ₀

ρ 0 C p

+ ( u ^V ) T — V{WT ) ,

V- u — 0 ,

где u — вектор скорости, ρ 0 — плотность жидкости при температуре T 0 , ν — кинематическая вязкость, g — вектор силы тяжести, направленный против оси z, β — коэффициент теплового расширения воды, T — температура, p —- давление, λ — коэффициент теплопроводности, C _p — теплоемкость.

Уравнение для температуры решается во всей расчетной области, включающей жидкость, диск и текстолитовую пластину. Твердые тела (диск и пластина из текстолита) моделируются методом погруженных границ [16, 17] . Динамика диска определяется уравнением Ньютона:

d V _— f p + f v dt m

где V — вектор скорости диска (согласно постановке задачи вертикальная компонента скорости задается равной нулю: V z = 0 ), m — масса диска, f p и f _v — силы давления и вязкие силы, действующие на диск со стороны жидкости. Эти силы рассчитываются путем интегрирования по всей поверхности диска, как горизонтальной, так и

вертикальной:

f p = ^P n dS, Γ b

f V = -У T w dS, Γ b

где τ w — вязкое напряжение на твердой поверхности , n — единичный вектор, перпендикулярный поверхности диска, dS — элемент поверхности, Γ _b — полная поверхность диска. Взаимодействие диска со стенками кюветы моделируется как неупругое столкновение. Диск не вращается вокруг своей оси.

В качестве граничных условий для скорости на всех границах расчетной области используются условия прилипания. Это значит, что скорость жидкости на границе с твердым телом равна скорости твердого тела:

uk =^{0 ,}

^{и |} Г ь = V ,

где Γ s — все границы расчетной области. На верхней границе расчетной области для температуры задаются условия третьего рода, остальные границы считаются адиабатическимиы:

∂T ∂n

= a(T - T ^ ), z=H

∂T ∂n

= 0 .

z=H

Здесь a — коэффициент теплоотдачи, Тж — температура окружающей среды. На верхней границе пластины из текстолита, сопряженной с жидкостью, ставится граничное условие на температуру с учетом падающего радиационного потока:

q \ z=S tex

∂T λ tex

∂n

- q rad ,

где q —- плотность теплового потока на границе между текстолитом и водой, λtex —- коэффициент теплопроводности текстолита, qrad —- поглощенный текстолитовой пластиной радиационный поток.

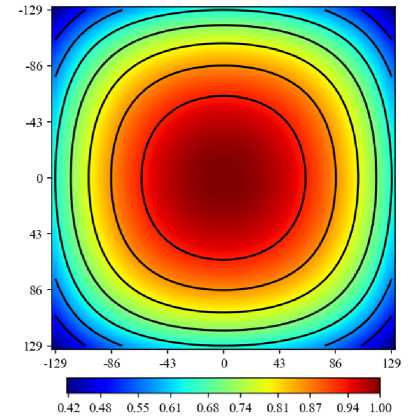
Рис. 2. Распределение падающего на поверхность текстолита излучения от ограниченного источника света при отсутствии диска

Распределение падающего на текстолит в отсутствие диска радиационного потока q _inc (x, у) рассчитывалось заранее на основе метода конечных объемов [18] с учетом как угла рассеивания светового потока лабораторными светодиодами (120 ° ), так и отражения от стенок кюветы. Результат расчета представлен на рисунке 2. Рассмотрен также и однородный нагрев — q _inc (x,y) =const .

Во всех случаях qrad qinc(x,y) 'П(x,y),                 (9)

при этом функция П(x,y) определяет, находится ли точка с координатами ( x,y ) в тени диска или за ее пределами:

П ( x,y ) =

1 ,

0 ,

| r ( x,y ) - r ( x c ,У с ) 1 >R, | r ( x,y ) - r ( x c ,У с ) | < R,

где r — радиус-вектор, x c и y c –– координаты центра диска, R — радиус диска.

Для численного моделирования применяется программный комплекс вычислительной гидродинамики «SigmaFlow» [19]. Расчетный алгоритм базируется на методе конечных объемов для неструктурированных сеток. Аппроксимация конвективных и диффузионных членов уравнения движения (1) выполняется на основе центральных разностных схем 2-го порядка. Взаимосвязь между полями скорости и давления реализуется с помощью процедуры расщепления типа SIMPLE. Для интегрирования по времени используется неявный метод Кранка–Николсон 2-го порядка точности. Конвективные члены уравнения переноса температуры аппроксимируются противопоточной TVD схемой 2-го порядка, нестационарный член уравнения температуры (2) — с помощью трехслойной схемы 2-го порядка.

Свойства воды соответствуют нормальным условиям, плотность диска р = 1300 кг/м ³ , теплоемкость и коэффициент теплопроводности диска и пластины из текстолита одинаковы: C p = 1300 Вт/(кг · К) и ^ tex = 0,38 Вт/(м - К). Окружающая среда имеет температуру Т _ж = 20 ° C и коэффициент теплоотдачи a = 50 Вт/(м ² • К), начальное значение температуры во всей расчетной области равняется 28 ° C. Средняя плотность радиационного потока составляет q inc = 150 Вт/м ² . В начальный момент времени пластина находится в центре кюветы (x c = 0 и y c = 0 ), скорость течения жидкости в кювете равна нулю.

В вычислительных экспериментах используется разделенная на две области неструктурированная ортогональная сетка, состоящая из шестигранных ячеек. В области движения диска и в верхней части текстолитовой пластины шаг сетки составляет 0.5 мм, а в остальной части кюветы — 1 мм. Сетка состоит из 7.3 млн ячеек и в процессе расчета не изменяется. Шаг по времени постоянный и равен 0.1 с. Максимальное значение числа Куранта в расчетной области не превышает 0.5. Время счета каждого варианта составляет 15000 с физического времени. Расчеты турбулентной конвекции проведены при помощи прямого численного моделирования с шагом сетки, меньшим колмогоровского масштаба и достаточным для разрешения всего спектра турбулентных пульсаций. Используемая для расчетов сетка позволяет получить сеточно-независимое решение.

• 3.    Результаты

Выполенны четыре варианта расчета конвекции: слой жидкости без диска с однородно нагреваемым дном (КО); слой без диска при неоднородном нагреве дна (КН); слой с плавающим диском и однородно нагреваемым дном (ДО); при неоднородном нагреве и плавающем диске слой с плавающим диском и неоднородно нагреваемым дном (ДН). Полагается, что однородный нагрев имитирует солнечное излучение, а неоднородный, который формируется вследсвие конечного размера источника света, — лабораторную установку. В таблице представлены все расчетные варианты и их основные интегральные характеристики: AT — разнность средней температуры верхней поверхности пластины из текстолита и свободной поверхности жидкости, число Рэлея Ra = двН 3 AT/vx и число Нуссельта Nu = (q H H ) / ( A A T ) , здесь x — температуропроводность, q H — осредненный тепловой поток с со свободной поверхности.

Таблица. Интегральные значения характеристик конвекции

Вариант	Описание	∆ T	Ra · 10 -6	Nu
КО	однородный нагрев без диска	1.19	5.67	9.98
КН	неоднородный нагрев без диска	1.19	5.63	9.64
ДО	однородный нагрев, плавающий диск	0.87	4.11	7.46
ДН	неоднородный нагрев, плавающий диск	0.85	4.05	7.37

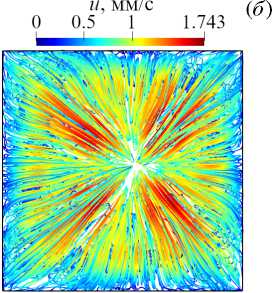
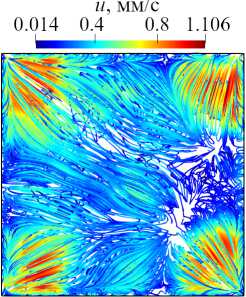
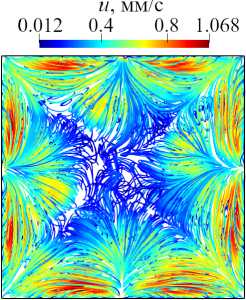
Структуру конвективных течений в слое для четырех расчетных вариантов иллюстрирует рисунок 3, на котором показаны линии тока, построенные для осредненных по всему времени расчета течений (вид сверху). При сравнении вариантов без диска (КО и КН, Рис. 3а , б ) видно, что при однородном распределении радиационного потока в кювете возникают ячеистые структуры, характерные для течения Рэлея–Бенара. При неоднородном нагреве образуется единый тороидальный вихрь с подъемным горячим течением в центре кюветы и опускным холодным течением по краям. Менее устойчивое и сложное по структуре течение в случае однородного нагрева приводит к тому, что помещенный в кювету диск достаточно часто оказывается в углах кюветы и задерживается там на время, необходимое для перестройки течения. Как следствие, на осредненной картине течения варианта ДО (Рис. 3в ) выделяются четыре области подъемных течений, расположенные в углах кюветы. При неоднородном нагреве устойчивое торообразное течение постоянно подтягивает диск к центру и препятствует его остановке. В результате осредненное течение в варианте ДН (Рис. 3г ) также наиболее интенсивно по краям кюветы, однако структура течения по периметру совсем иная: вдоль каждой стороны наблюдается по две области подъема жидкости, смещенные от углов примерно на одну четверть длины стороны кюветы. Стоит отметить, что независимо от распределения радиационного потока, который влияет и на структуру течения (см. Рис. 3) и, как следствие, на траекторию движения диска (Рис. 4) , осредненные по времени интегральные показатели близки (см.Таблицу).

Характер движений диска при однородном и неоднородном освещении иллюстрирует рисунок 4, на котором для вариантов ДО и ДН приведены траектории перемещения центра диска и осредненное по времени положение тени от диска. При этом осреднение в варианте ДО производится с момента начала движения диска, а в варианте

( а )

( в )

( г )

Рис. 3. Линии тока осредненных течений в отсутствие диска – варианты КО ( а ) и КН ( б ), и с плавающим диском – варианты ДО ( в ) и ДН ( г )

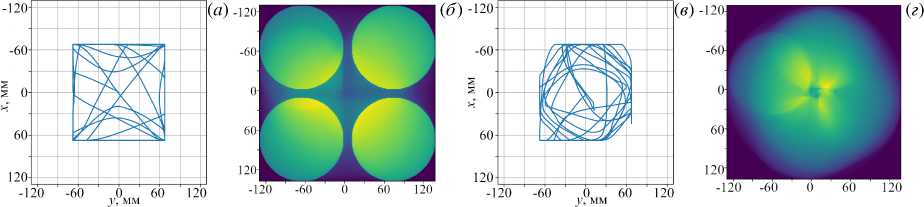
Рис. 4. Перемещения диска в слое при однородном ( а ), ( б ) и неоднородном ( в ), ( г ) освещении: траектории движения центра диска ( а ), ( в ); осредненное по времени положение тени от диска ( б ), ( г )

ДН только c 10000 c, когда диск выходит на устойчивый режим (см. Рис. 5) . Траектория движения центра диска для варианта ДО представлена на рисунке 4а . Видно, что диск в основном находится в углах кюветы и лишь изредка пробегает через центральную часть. На рисунке 4б показано осредненное по времени положение тени диска. Четкие края изображения диска в углах кюветы говорят о том, что диск в этом положении пребывает длительные интервалы времени и сохраняет неподвижность. Если же посмотреть на аналогичные изображения для ДН (Рис. 4в , г ), то видно, что в этом случае диск практически не заходит в углы кюветы, а движется от центра одной стенки кюветы к центру другой. В этом варианте поле осредненного положения диска (Рис. 4г ) характеризуется отсутствием четких границ и наибольшей вероятностью его нахождения в центре кюветы.

Исследования двумерных блужданий диска в слое с изотермической нижней границей показали, что, несмотря на хаотичность пространственных траекторий, движение вдоль каждой координаты относительно упорядочено и похоже на движения диска в узкой кювете, в которой у него имеется только одна степень свободы [13]. Этот факт побудил проследить за движением диска по каждой координате и радиационном нагреве. Изменения во времени координат центра диска xc и yc показаны на рисунке 5. Видно, что при однородном нагреве (Рис. 5а) перемещение диска по каждой координате выглядит как квазипериодическое движение, хотя общая картина перемещений такого впечатления не создает (Рис. 4а). При неоднородном нагреве существенно сокращается время остановок у стенок (Рис. 4б). При визуальном наблюдении сверху за движениями диска при однородном нагреве они выглядят как случайные перемещения вдоль периметра с остановками в углах, а при неоднородном — скорее как перемещения по ромбообразной траектории, причем на второй половине расчета доминируют движения против часовой стрелки. Такую картину подтверждают показанные на рисунке 5в, г зависимости угловой скорости движения диска относительно центра кюветы. Угловая скорость определяется как r x V и =----,

r • r здесь r = r (xc ,yc) — радиус-вектор центра диска относительно цента кюветы. Этот параметр позволяет установить направление вращения диска вокруг центра кюветы. Для варианта ДО (Рис. 5в) график угловой скорости выглядит как последовательность импульсов с примерно постоянной скважностью и случайным знаком. В варианте ДН (Рис. 5г) скважность заметно изменяется со временем, а примерно к 10000 с диск выходит на некоторый

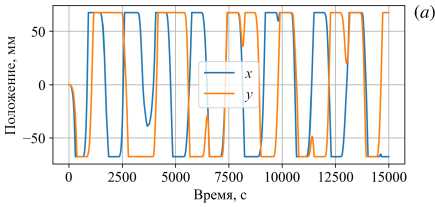
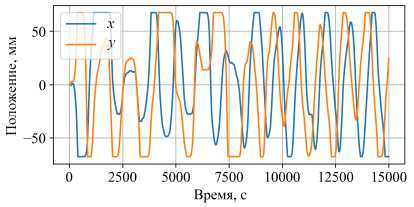
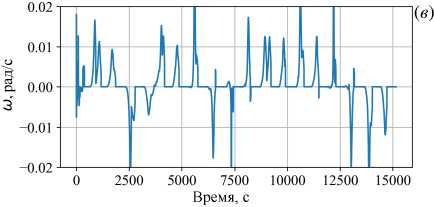
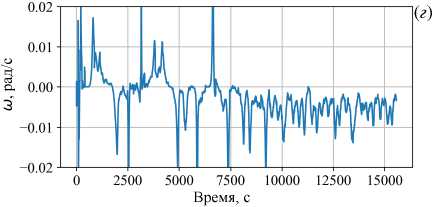
Рис. 5. Движение диска в проекциях на оси x ( а ) и y ( б ); угловая скорость диска относительно центра кюветы при однородном (ДО) ( в ) и неоднородном (ДН) ( г ) нагреве

квазистационарный режим движения, характеризуемый вращением вокруг центра кюветы в одном направлении. Надо отметить, что на временных зависимостях перемещений диска (Рис. 4б ) и его угловой скорости при варианте ДН хорошо видна смена режима: на начальном интервале (примерно до 7500 с) его характеристики похожи на отвечающие варианту ДО, однако затем характер движений принципиально меняется.

Следует напомнить, что в слое имеет место достаточно развитый конвективный режим (Ra ≈ 5 · 10 ⁶ ), обеспечивающий интенсивный перенос тепла за счет мелкомасштабных конвективных структур. Поле температуры в горизонтальном сечении между диском и текстолитовым дном кюветы (z = 1 . 5 мм) показано на рисунке 6 в разные моменты времени для варианта ДО. На всех рисунках разброс температуры в сечении составляет примерно 1.5 ^o C. Вне диска видны характерные для конвекции ячеистые структуры, размеры которых меньше в нагретой области и больше в холодных областях. Под диском ячеек нет, что говорит о преобладании диффузионного переноса тепла. За время, пока диск стоит в углу, температура воды под ним снижается, так как он перекрывает радиационный поток. После отплытия диска некоторое время еще сохраняется пониженная температура, что свидетельствует о влиянии тепловой инерции дна.

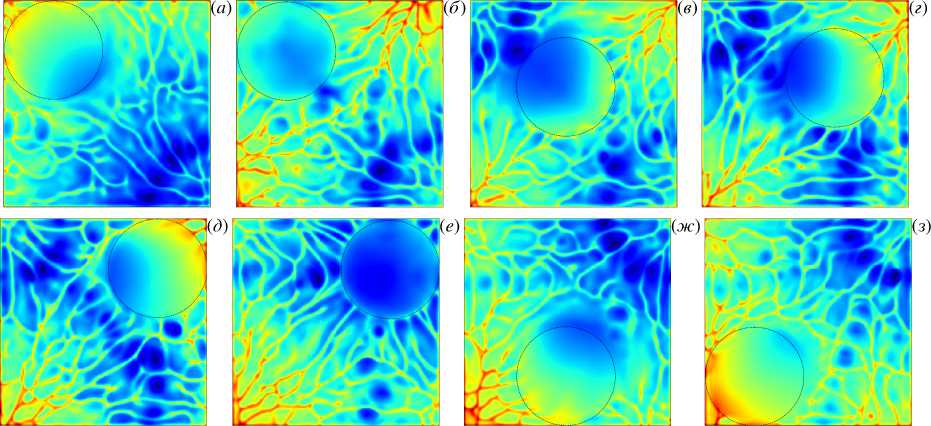
Рис. 6. Поле температуры в горизонтальном сечении z = 1 . 5 мм для варианта ДО в различные моменты времени после начала расчета t , c: 12300 ( а ), 12786( б ), 13002 ( в ), 13009 ( г ), 13179 ( д ), 13716 ( е ), 13941 ( ж )и 14031 ( з ); положение диска обозначено пунктиром; разброс температуры на всех рисунках составляет примерно 1 . 5 ° C

Интересно рассмотреть отдельные стадии движения диска. На рисунке 6а диск находится в верхнем левом углу (момент прибытия). Спустя 486 с течение в кювете перестраивается, диск отрывается, движется к центру кюветы (Рис. 6в ), но затем меняет направление, устремляется в горячий верхний правый угол (Рис. 6г ) и достигает его (Рис. 6д ). При этом сохраняется выраженная холодная диагональ. Спустя 537 с диск отрывается от верхнего правого угла. Стоит отметить, что в этом углу диск стоит дольше, чем в предыдущем, и вода под ним охлаждается сильнее (Рис. 6e ). Далее диск смещается в сторону самой горячей части кюветы — нижнего левого угла, но ненапрямую, а сначала к центру нижней грани (Рис. 6е ) и только после этого попадет в нижний левый угол (Рис. 6ж ). В целом можно сделать вывод, что при движении в сторону более нагретой области кюветы диск чаще всего попадает в угол, после чего требуется значительное время на перестройку и формирование течения, достаточно интенсивного, чтобы вытащить диск из застойной угловой зоны.

В варианте ДН (Рис. 7) структура поля температуры иная. В выбранном горизонтальном сечении формируется ромбовидная структура более горячей воды между центрами граней кюветы. Диск двигается по этой «горячей

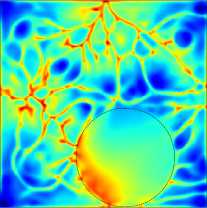
( a )

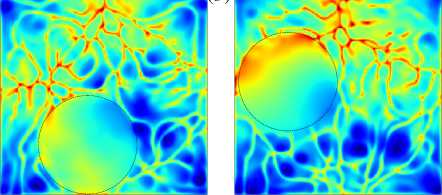
Рис. 7. Поле температуры в горизонтальном сечении z = 1 . 5 мм для варианта ДН, в различные моменты времени после начала расчета t , c: 12303 ( а ), 12480 ( б ), 12669 ( в ), 12897 ( г ). Положение диска обозначено пунктиром. Разброс температуры на рисунках составляет 1 ^° C

( г )

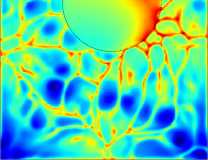
дорожке и сглаживает ее, но после его прохода дорожка восстанавливается. Плавающий диск может скользить по грани (Рис. 7а , б ), не доплывать до грани и поворачивать (Рис. 7в ), а может и отскакивать при соприкосновении, что показано на рисунке 7г . При этом разброс температуры по сечению в варианте ДН чуть меньше, чем в варианте ДО — около 1 ^о C . Это связанно с тем, что диск практически не останавливается и препятствует формированию нагретых и охлажденных областей.

• 4.    Лабораторный эксперимент

Лабораторная модель выполнена в соответствии с рисунком 1. Нижняя граница (основание) изготовлена из стеклотекстолита толщиной 10 мм и нагревается падающим от светодиодной панели радиационным потоком. Для лучшего поглощения света поверхность основания, контактирующая с водой, окрашена в матовый черный цвет. Распределение теплового потока на нижней границе напрямую связано с освещенностью, которая определяется с помощью люксметра. Измерения показывают, что освещенность максимальна в центре кюветы и уменьшается по направлению к периферии, отличие достигает 15%. В основании имеется девять отверстий, в которых установлены медь-константановые термопары. Спаи термопар располагаются на границе жидкость–основание и измеряют температуру жидкости вблизи дна. Верхняя граница является свободной, и отвод тепла с нее осуществляется за счет теплообмена между жидкостью и воздухом. Для оценки перепада температуры между двумя горизонтальными границами и, соответственно, числа Рэлея, вблизи свободной границы устанавливаются две термопары, которые не мешают движению диска. Спаи термопар погружены на глубину 1 мм.

Геометрические размеры кюветы и диска, расстояние между основанием и диском, параметры рабочей жидкости в эксперименте и в численном моделировании одинаковы. Диск удерживается на необходимой высоте за счет поплавка, закрепленного на оси диска (конструкция описана в работе [13] ). Кроме диска с зеркальной поверхностью, эксперименты проведены и с дисками, пропускающими часть падающего света. Под коэффициентом пропускания K понимается отношение проходящего потока излучения к падающему.

На рисунке 8 представлены траектории перемещения центра диска в экспериментах с зеркально отражающим диском и с дисками, имеющими разный коэффициент пропускания. Характер перемещений соответствует скорее рисунку 4а , чем рисунку 4в , то есть однородному падающему радиационному потоку, хотя интенсивность потока на периферии на 15% ниже. Если диск пропускает четверть падающего на него светового потока, то характер его движения становится менее устойчивым (Рис. 8 б ), апри коэффициенте пропускания K =0 . 4 диск прибивается к одной из стенок и «топчется» вблизи нее.

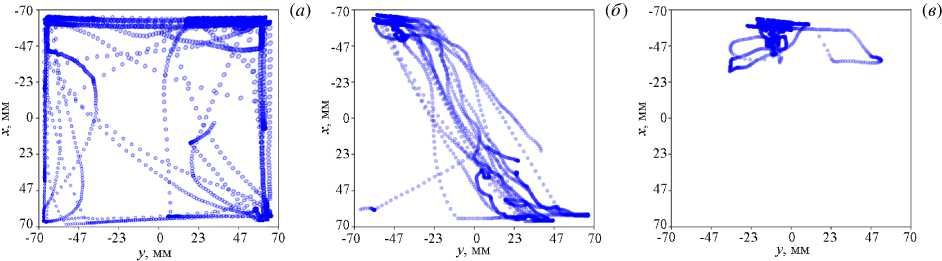
Рис. 8. Траектории движения центра зеркально отражающего диска ( а ) и дисков с конечным коэффициентом пропускания K : 0.25 ( б ) и0.4 ( в )

По результатам эксперимента с зеркальным диском на рисунке 9 построены перемещения по каждой из координат (в таком же представлении, как и на рисунке 5а , б ). Хотя двумерный график перемещений напоминает скорее движения в однородно нагреваемом слое, одномерные проекции сочетают в себе характерные особенности вариантов ДО и ДН. Это можно объяснить тем, что при численном моделировании неоднородность нагрева заметно больше, достигает 50%, в то время как в эксперименте она не превышает 15%. Как следствие, в эксперименте диск совершает движения в основном вблизи стенок, однако время приостановок сильно варьируется.

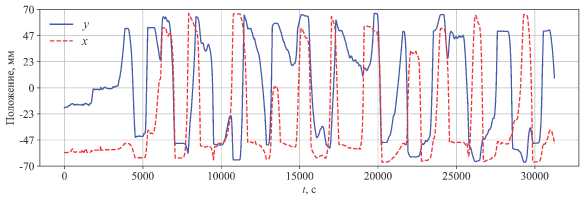
Рис. 9. Изменения положения диска по координатам x и y (эксперимент с зеркальным диском)

Для количественного сравнения результатов численного расчета и эксперимента используются две характеристики: средняя скорость перемещения диска в «активной фазе» и среднее время полного цикла его движения от одной грани кюветы до противоположной. Среднее время полного цикла для вариантов ДО и ДН составляет, соответственно, примерно 400 и 580 с, а для эксперимента — около 500 с. Средние скорости перемещения диска равны 0.73 мм/с для ДО, 0.47 мм/с для ДН и 0.8 мм/с в эксперименте. Приведенные данные показывают, что экспериментальные величины в целом неплохо согласуются с данными расчетов. Скорость перемещения в эксперименте ближе к скорости при варианте ДО, а среднее время полного цикла имеет промежуточное между случаями ДО и ДН значение.

• 5.    Заключение и дискуссия

Проведено численное моделирование двумерных движений диска с зеркальной верхней поверхностью, свободно плавающего в протяженном слое жидкости. Дно заполненной жидкостью кюветы квадратного сечения нагревается падающим сверху радиационным излучением. Показано, что в режиме турбулентной конвекции крупный диск (диаметром чуть меньше половины стороны квадрата) совершает в слое хаотические перемещения, перестраивая как локальную, так и интегральную структуру конвективного потока, но слабо меняя интегральные показатели тепломассопереноса. Помимо основных управляющих параметров, таких как числа Рэлея и Прандтля, относительные размеры и форма диска, сильное влияние на динамику тела оказывают его оптические свойства и пространственное распределение нагрева, которым в проведенном исследовании уделено основное внимание.

Результаты расчетов выявили чувствительность системы к степени однородности падающего излучения. Изменение его распределения приводит к трансформации структуры осреднненной крупномасштабной циркуляции. При однородном распределении формируется тороидальный вал с опусканием жидкости в центральной части, а при неоднородном распределении с максимумом нагрева в центре, наоборот, образуется вал с подъемом жидкости в центре. Так как движение плавающего тела определяется крупномасштабными течениями жидкости, их перестройка приводит к качественным изменениям в пространственных и временных характеристиках перемещения диска. При однородном распределении излучения тороидальный вал сносит расположенный в нижней части слоя диск к боковым стенкам, и основную часть времени он движется вдоль них с остановками в углах кюветы. Неоднородное распределение излучения способствует возникновению тороидального вала с противоположным вращением, который, наоборот, старается сместить диск к центру. В результате диск хаотически блуждает в центральной области.

Лабораторный эксперимент при близких характеристиках нагрева подтвердил случайный характер блужданий диска и дал близкие значения для средней скорости движения диска и характерного интервала времени для перемещения диска от одной стенки к другой.

Эксперименты с дисками, имеющими разный коэффициент пропускания излучения K , показали, что при значении K ⩾ 0 . 4 блуждания диска прекращаются. Этот результат подтверждает выводы, полученные в экспериментах с одномерными передвижениями диска в вытянутой кювете, в которых устойчивые блуждания возникали только при зеркальной поверхности диска [14] , и при численном моделировании одномерных блужданий диска с переменным коэффициентом пропускания [15] . Таким образом, зависимость динамики диска от коэффициента пропускания сохраняется и при наличии двух степеней свободы. Надо отметить, что данный эффект обусловлен граничными условиями второго рода на нижней границе (постоянный поток тепла). В случае задания постоянной температуры при рассматриваемом аспектном отношении и близких значениях числа Рэлея остановка диска не наблюдалась [13] . Принципиально различное поведение диска при однородных граничных условиях первого и второго рода обусловлено тем, что в одном случае поток тепла с нижней границы зафиксирован (ГУ второго рода), а в другом (ГУ первого рода), рассмотренном в [13] , теплопоток с нижней границы под диском существенно снижается.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 22-61-00098),