Большие деформации изгиба неоднородного бруса

Цель настоящей работы состоит в исследовании влияния неоднородности свойств материала бруса на его равновесие и устойчивость при чистом изгибе при учете больших деформаций. Чистый изгиб, как известно, — одна из базовых деформаций, которая активно используется для экспериментального определения и уточнения параметров моделей как чисто упругого, так и нелинейно-упругого поведения сред. Появление новых высокоэластических конструкционных материалов, а также существенный рост внимания к задачам моделирования биологических субстанций и их искусственных заменителей, способных, в частности, выдерживать большие деформации, вызывает новую волну интереса к теоретическим задачам и экспериментальным методикам, позволяющим строить корректные и верифицируемые математические модели сплошных сред. Еще одной из причин, заставляющих обращаться к классическим задачам, является интенсивное изучение, моделирование и расчет процессов создания, проверки работоспособности композиционных материалов, представляющих собой матрицу с относительно жесткими волокнами, обладающими предопределенными свойствами [1]. Так, в работе [2] показано, что расчет на прочность таких микро-конструкций настоятельно требует учета вероятности разрушения композита вследствие потери устойчивости.

Подробный анализ различных аспектов равновесия однородного нелинейно-упругого бруса дан в работе [3], где показано, что в большинстве общеупотребительных моделей нелинейно-упругих

материалов на диаграмме нагружения имеется точка максимума, что свидетельствует о возможной потере устойчивости при изгибе. В работах [4-8] с использованием бифуркационного анализа для однородного бруса решен ряд конкретных задач устойчивости при больших деформациях изгиба. В настоящей работе аналогичный подход применяется при более сложной модели: ее материальные параметры являются функциями вертикальной координаты — положения точки по толщине бруса. Изучается зависимость между положениями на диаграмме изгиба точки максимума и точки потери устойчивости, а также влияние на эту зависимость неоднородности материала двух типов.

2.    Полуобратное представление изгиба бруса

Рассмотрим для сплошной среды следующее полуобратное преобразование:

R = P ( x ), Ф = By , Z = z .                                    (1)

Здесь: x , y , z — декартовы координаты в отсчетной конфигурации упругого тела; R , Ф , Z — цилиндрические координаты в его деформированной (текущей) конфигурации; B — положительная постоянная. Выражения (1) описывают деформацию изгиба бруса прямоугольного поперечного сечения шириной h и толщиной a , нагруженного торцевыми моментами. В результате деформации сечение бруса приобретает форму кругового сектора с углом раствора у . При этом функция P ( x ) представляет собой радиус точки бруса в деформированном состоянии, параметр B = у/ h пропорционален углу у , а Ф является углом отклонения радиуса точки от направления координатной оси x (Рис. 1).

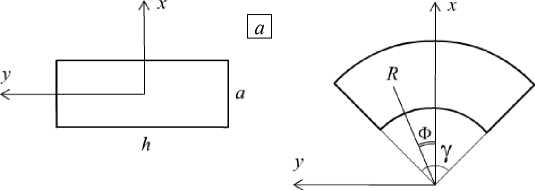
Рис. 1. Изгиб бруса: состояние до ( а ) и после ( б ) деформации

Геометрические характеристики деформации — ее градиент C , левый тензор искажений U , тензор поворота A , мера деформации Коши-Грина G и ее главные инварианты I_k , соответствующие преобразованию (1), определяются следующими выражениями:

C = P' i x e R + ^{BP i} y e Ф + i z e Z ,

U = ( C ■ C ^T ) ¹² = P' i x i x + BP i y i y + i z i z ,

A = i x e R ⁺ i y e Ф + i z e Z ,

G = U ² = P '² i_xi_x + B ² P ² i_yi_y + i_zi_z , xx       yy zz

• 1 1    = tr G = P ‘ ² + B ² P ² + 1,

• 1 ₂    =1 ( tr G ² + tr² G ) = P '² B² P² P '² + B² P ²,

• 1 ₃    = det G = B ² P ‘ ² P ².

В (2) { i x , i _y , i _z } и { e _R , e _Ф, e _Z } — ортонормированные базисы декартовых координат в отсчетной конфигурации и цилиндрических координат в текущей конфигурации соответственно; штрихом обозначено дифференцирование по переменной x .

Определяющее соотношение для сжимаемого упругого материала имеет вид dW dC ’

где D — тензор напряжений Пиола, W — функция удельной потенциальной энергии деформации. Соотношение (3) может быть уточнено в зависимости от выбранного аргумента функции удельной потенциальной энергии. Так, в изотропном случае эта функция зависит либо от главных инвариантов левого тензора искажений, либо от главных инвариантов меры деформации Коши:

d W d W

D =-- A = 2-- C .

dU dG

Краевая задача изгиба бруса, состоящая из уравнений равновесия и граничных условий, выражающих отсутствие напряжений на верхней и нижней гранях, имеет следующий вид:

div D =0,

i x ■ D I x =± a! 2 .

С учетом (1), (2), (4) и конкретизации модели материала, то есть после выбора функции удельной потенциальной энергии W , система (5) сводится к нелинейной, вообще говоря, краевой задаче для дифференциального уравнения второго порядка. В результате его решения определим функцию P ( x ) .

Основной характеристикой данной задачи является диаграмма изгиба — график зависимости изгибающего момента от угла изгиба сечения бруса у или, что эквивалентно, от параметра B . Изгибающий момент вычислим по формуле

R ₁

M = f^ PdR ,                               (6)

R ₀

в которой с_фф = e _ф- T ■ e _ф — диагональная компонента тензора напряжений Коши T = ( det C ) C T ■ D ; R ₀ , R ₁ — внутренний и внешний радиусы деформированного сечения бруса; Т — символ операции транспонирования.

Следует отметить, что как процесс вывода обыкновенных дифференциальных уравнений краевой задачи (5), так и их численный анализ является весьма трудоемким, особенно для сложного многопараметрического выражения функции W . Быстрое и надежное решение таких задач осуществимо с с помощью компьютерной системы автоматизации полуобратного метода нелинейной теории упругости, представленной в [9].

• 3.    Исследование изгиба бруса из сжимаемого материала

  • 3.1.    Использованные модели материалов

При рассмотрении равновесия и устойчивости бруса будем базироваться на численно-аналитической схеме [3, 4]. Для описания нелинейно-упругого поведения материала бруса выберем распространенные модели полулинейного (гармонического) материала и материала Блейтца и Ко, выражения для функций удельной потенциальной энергии которых, соответственно, записываются в виде [10]:

Wharmonic = Ца1 1 U - E )+ Ц 11 [(U - E У ] ,

Wbk = Ц 2 (1 -в)

1213-1 + 1 (13a-1)- 3 + Ц1 в 11 + 1 (13-a- I)- 3 av ’         2 av ’

В (7), (8) приняты обозначения: a , в , Ц — параметры материала; E — единичный тензор. При малых деформациях ц имеет смысл модуля сдвига, параметр a связан с коэффициентом Пуассона v соотношением a = v/ (1 - 2 v ), а в является чисто нелинейным и характеризует жесткость материала в области сверхвысоких деформаций.

Подставляя последовательно (7) и (8) в (4), получим для этих моделей определяющие соотношения, записанные в терминах тензора напряжений Пиола:

D e monic = 2 ц [( « 1 1 U - E ) - 1 ) A + C ] ,

D _BK = ц [ (1 - в ) 1 ₃ ^{- 1} ( l 1 E - G + ( 1 ₃ ^{a+ 1} - 1 ₂) G ^{- 1} ) + в ( E - 1 Г G - 1 ) ] ■ C .

В случае полулинейного материала краевая задача для определения функции P ( x ) (5) является линейной. Задачи же для материала Блейтца и Ко нелинейны. Подробная схема их численно-аналитического исследования представлена в [3]. Заметим, что явное аналитическое решение линейной задачи для гармонического материала необходимо, во-первых, для верификации численных методов, которые применяются в других моделях материала, а во-вторых, оно служит начальным приближением при итерационных схемах нелинейного анализа.

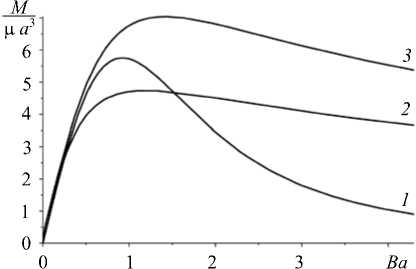
Рис. 2. Зависимость изгибающего момента от угла изгиба         Некоторые выводы о потере устойчивости процесса нагружения можно сделать на основе рисунка 2, на котором приведены зависимости изгибающего момента (6) от угла изгиба сечения для бруса с соотношением размеров к/a = 2,5 и значением параметра а = 0,5. Для всех кривых характерен

«падающий участок», который можно рассматривать как один из признаков потери устойчивости при нагружении. Кривая 1 соответствует модели полулинейного материала (7), кривые 2 и 3 отражают поведение бруса в случае модели материала Блейтца и Ко (8) при в = 0 и в = 1 соответственно.

• 3.2.    Равновесие неоднородного бруса

Для того чтобы изложенная выше схема полуобратного метода осталась применимой без существенных изменений к неоднородному брусу, ограничимся случаем, когда материал бруса неоднороден только по толщине, то есть по координате x (см. Рис. 3). При этом будем считать, что изменяется только один из материальных параметров, а именно модуль сдвига ц . Данное допущение не является принципиальным, но позволяет сравнивать результаты с представленными в работах [3, 4], где в расчетах при всех моделях использовалось одно и то же значение коэффициента Пуассона, равное 1/4, что соответствует параметру а = 1/2 .

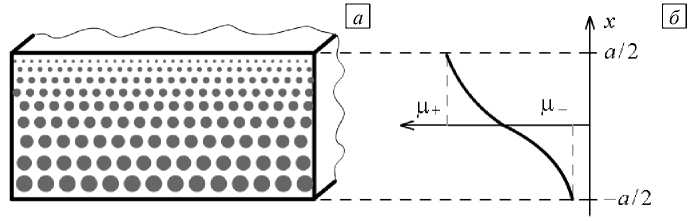
Рис. 3. Неоднородность свойств по толщине бруса ( а ); характер изменения модуля сдвига ц ( б )

В работе представлены результаты для двух типов сдвиговой неоднородности:

• -    линейная ц ( x ) = ц ₀ ( ( 3/ a ) x + 1 + 5/2 ) ;

• -    экспоненциальная ц ( x ) = ц ₀ exp ( (5/ a )( x + a /2) ) ,

но в обоих случаях ц _ ^ц ( - a /2) = ц ₀, а ц₊ ^ ц ₀ 5 и ц₊ ^ ц ₀ exp( 5 ) для линейной и экспоненциальной зависимостей соответственно.

В качестве примера решим нелинейную краевую задачу изгиба неоднородного бруса из упрощенного материала Блейтца и Ко ( в = 0):

P 4x) = -

1 BP ( x ) f ' ( x ) P ' ( x )⁴

3        f ( x )         3

P ' ( x )³ BP ( x ) - 1 = 0,

1 f ' ( x ) P ' ( x ) 1 P ‘ ( x ) +------

, 4

f (x)     3 B2P(x)3 ’ x = ± a] 2.

В (9) использовано выражение f ( x ) = ц ( x )/ ц ₀, а штрихом обозначено дифференцирование по переменной x .

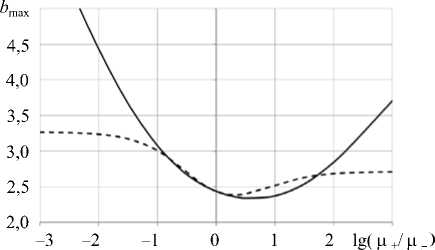
Рис. 4. Точки максимума на диаграмме нагружения: пунктирная линия - линейная неоднородность, сплошная линия - экспоненциальная неоднородность

Некоторые результаты численного исследования этой краевой задачи представлены на рисунке 4. Проследим влияние неоднородности на упомянутую выше характеристику диаграммы нагружения — ее точку максимума; безразмерный параметр b введен соотношением b = Ba, в котором величина B пропорциональна углу у . Видно, что для бруса с более мягкой нижней гранью (ц_ < ц+) точка максимума всегда смещается в область больших углов изгиба. Влияние неоднородности в случае более жесткого нижнего слоя неоднозначно: при неоднородностях уровня ц+/ц_<10

наблюдается небольшое смещение точки максимума вниз, в область меньших деформаций, однако при увеличении неоднородности максимум начинает увеличиваться. Такое качественное поведение характерно для обоих рассмотренных типов неоднородности.

• 3.3.    Устойчивость неоднородного бруса

Устойчивость неоднородного бруса при изгибе рассмотрим в рамках бифуркационного подхода на основе метода наложения малой деформации на конечную [10]. Для этого в полуобратное преобразование (1) добавим возмущения, пропорциональные малому параметру £ :

R = P ( x ) + £ U ( x , y ),    Ф = B ( y + £ V ( x , y )),    Z = z .

По представлению (10) генерируется краевая задача (5), в которой удерживаются слагаемые с параметром £ только первого порядка. Наличие нетривиальных решений этой задачи, то есть возмущений, существующих в окрестности основного решения, и считается критерием потери устойчивости. Математический процесс такого анализа изложим ниже.

На первом этапе исследования к линеаризованной краевой задаче применим метод разделения переменных по схеме:

U ( x , y ) = u ( x )cos(2 n ny/h ),     V ( x , y ) = v ( x )sin(2 n ny/h ).

Такое представление, во-первых, сводит систему уравнений в частных производных к краевой задаче для системы обыкновенных дифференциальных уравнений, а во-вторых, позволяет автоматически выполнить на боковых гранях бруса граничные условия, означающие скользящую заделку: отсутствие как касательных напряжений и их возмущений, так и угловых смещений на этих поверхностях ( V ( x , ± hl 2 ) = 0 ). Краевые условия в (5) линеаризуются и означают теперь, что на верхней и нижней гранях бруса нет добавочных напряжений.

Таким образом, приходим к однородной краевой задаче, состоящей:

• - из уравнений равновесия

u" = D 11 ( x , p ) u ' + D ₁₂ ( x , p ) v' + D ₁₃ ( x , p ) u + D ₁₄ ( x , p ) v , v" = D ₂₁ ( x , p ) u ' + D ₂₂ ( x , p ) v' + D ₂₃ ( x , p ) u + D ₂₄ ( x , p ) v ,

- краевых условий u' = A11( x, p) u + A12( x, p) v, v' = A21( x, p) u + A22( x, p) v в точках x = - a/2 и x = a/2. Через p в (12) обозначен набор параметров (номер моды n, геометрические характеристики, угол изгиба).

Исследование существования нетривиальных решений задачи (11), (12) реализуем по следующей схеме. Рассмотрим последовательно две задачи Коши для системы (11). Решение первой из них обозначим через ( u ₁ , v ₁ ) , начальные условия выберем в виде:

U1(- a/2) = 1,            V1(- a/ 2) = 0,(13)

u'(- a/2) = ^ii(- al 2),    v'(- a] 2) = A21(-a/2).(14)

Начальные условия для второй задачи зададим как u 2(- a/2) = 0,           v 2(- a/2) = 1,(15)

u 2(- a/ 2) = A12(- a/ 2),   v 2(- a/2) = A22(- a/ 2).(16)

Легко увидеть, что в силу (13), (15) эти решения будут линейно независимыми, а в силу (14), (16) оба они будут удовлетворять краевому условию (12) в точке x = - a /2 . Следовательно, общее решение системы (11), при котором выполняется краевое условие (12) при x = - a /2 , может быть записано в виде:

u = Cmum , v = Cmvm   ( m = I,2), где Cm — произвольные постоянные. С учетом представления (17) для определения констант Cm получаем линейную систему уравнений, которая имеет нетривиальные решения, если ее определитель

A =

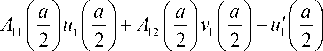
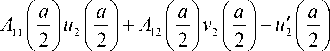
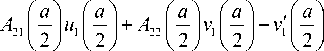
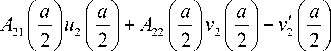
обращается в нуль. В силу изложенного этот определитель является функцией вектора p параметров системы. Поиск точек бифуркации состоит теперь в поиске нулей этого определителя как функции параметра нагружения (изгибающего момента или угла изгиба) в зависимости от геометрических размеров и номера моды.

В качестве примера ниже приведены выражения для коэффициентов линеаризованной краевой задачи (11), (12) в случае линейной неоднородности. Введены безразмерные величины £ = x/a , p = P]a , L = h/a , при этом штрих означает дифференцирование по безразмерной координате ^ :

D11 = 51 L2(8p'3p5b35- 2p4b25 + 8p'3p5^ + 4p'3p5- 8p'3p),D12 = 51 L (4р'р4л b 25 n ^ + 2p'3p2n5 n + 4p'3p2n n),

D ₁₃ = 5 ( L ²p' ⁴ 5 (2 p ⁴ b ³ - 6 ^ - 6) - 4 p‘ ² p ² п ² 5 n ² (2 ^ + 1) - 8 p' ² p V n ² - 3 L ²p' ⁴ 5 ),

D ₁₄ = 4 5 1 L ( p' ⁴ p ⁵ v n b ³ 5 n - 2 p' ⁴ p v n5 n ^ - p' ⁴ p v n5 n - p' ⁴ p v n n ),

D ₂₁ = 5L ( p ⁵ n b ⁴ n ( - 6 5^ - 5 - 6) - p' ² p ³ n b ² n (6 ^5 + 3 5 + 6)),

D ₂₂ = 5 ₂ L ² (2 p' ⁴ p ⁶ b 5 5 - p'p ⁵ b 4 5 + p V b ² (2 5^ + 5 + 1)),

D ₂₃ = 5 ₂ n L ( -p' ⁵ 5 n (2 p ⁴ b ³ + 2 ^ + 1) - p^{, 3} p ² b 2 5 n (6 ^ - 3 5 + 6) - 4 p^{, 2} p ³ b 2 5 n - 2 p' ⁵ ( 5 + 1)),

D ₂₄ = 18 5 ₂ p' ³ p V b ² n ( - 2 5 - 1 - 32 p' ³ p ³ n ² b ² n ),

A 11 = -p' ⁴ b / 3,    A 12 = - 2 p' ⁴ pn bn I (3 L ),

A21 = -2nn (b3p3p'3 - b2p2 -p'2)/(Lp'p2b2),    A22 = 0 , где S1    3L2p4b2(25^ + 5 + 2),

5, =

²    3 L ²p'p ⁵ b ⁴ (2 5^+ 5 + 2)

.

Из приведенных формул видно, что коэффициенты линеаризованных уравнений зависят от функции P ( r ) , описывающей основное решение, устойчивость которого является предметом исследования.

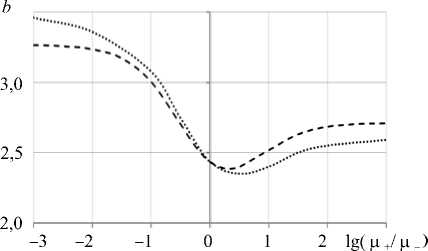
Рис. 5. Критические углы изгиба (точечная кривая) в сравнении с точками максимума диаграмм нагружения (пунктирная кривая)

В тех случаях, когда краевые задачи, рассматривающие равновесие изгибаемой панели, не имели аналитического решения, они реализовывались численно. Для каждого значения параметра нагружения или параметра деформации (например параметра B, пропорционального углу изгиба) численно решалась нелинейная краевая задача относительно функции P ( r ) , что позволяло численно задать коэффициенты уравнений линейной задачи.

Рисунок 5 демонстрирует расположение критических точек, ближайших к точке максимума диаграммы нагружения, для случая линейной неоднородности. Видно, что у бруса с более мягкой нижней гранью точки бифуркации появляются раньше точек максимума, следовательно, такой брус теряет устойчивость на возрастающем участке диаграммы изгиба. Однородный брус и брус с более жесткой нижней гранью теряют устойчивость в окрестности точки максимума, но после того, как минуют ее. Экспоненциальная модель неоднородности приводит к качественно аналогичным результатам.

4.    Заключение

В работе представлено приложение полуобратного метода нелинейной теории упругости к задаче исследования влияния неоднородности свойств материала бруса на его равновесие и устойчивость при чистом изгибе с учетом больших деформаций. Двумерная задача равновесия сведена к нелинейной краевой задаче для обыкновенного дифференциального уравнения второго порядка. Показана применимость данного подхода при различных типах поперечной неоднородности, причем степень этой неоднородности может быть высокой, вплоть до трех порядков по величине. Рассмотрено влияние неоднородности на обнаруженную в предыдущих работах особенность диаграммы изгиба нелинейно-упругих материалов — наличие точки максимума, за которой следует падающий участок. Установлено, что если степень неоднородности материала велика, то есть значения упругих модулей на верхнем и нижнем слоях отличаются более чем в десять раз, влияние неоднородности состоит в смещении точки максимума в область больших деформаций.

Для исследования устойчивости изгибаемого бруса использован бифуркационный анализ. Изучено влияние неоднородности материала бруса на зависимость между положениями на диаграмме изгиба точки максимума и точки потери устойчивости. Установлено, в частности, что для бруса с более мягкой нижней гранью точки бифуркации расположены левее точек максимума, то есть брус теряет устойчивость на возрастающем участке диаграммы.

Представляется, что полученные результаты могут быть полезны при разработке и развитии новых экспериментальных методов идентификации параметров математических моделей, описывающих механические свойства материалов и конструкций, испытывающих большие деформации.

Работа выполнена в рамках проекта «Моделирование деформирования функционально-градиентных композитов и многофазных сред» Программы фундаментальных исследований Президиума РАН по стратегическим направлениям развития науки.