Брэгговская СВЧ-структура в коаксиальном волноводе как датчик контроля диэлектрических параметров жидких сред

Периодические структуры с эффектом возникновения запрещенных зон, обусловленных брэгговским отражением, встречаются во многих областях науки и техники, но наибольшее распространение получили в оптическом диапазоне. Именно в оптике впервые создаются измерительные преобразователи на основе волоконной решетки Брэгга и фотонных кристаллов [1]. Переложение уже нашедших отражение в ряде прикладных задач принципов анализа и синтеза оптических резонансных сенсоров в область радиочастот может раскрыть новые стороны и области применения известных и хорошо изученных функциональных элементов.

Рядом авторов была проведена аналогия с широко известными оптическими периодическими структурами, такими как волоконно-оптические решетки Брэгга и фотонные кристаллы с целью выявления в радиочастотном аналоге новых, ранее не используемых на практике свойств [2–4]. Одним из таких направлений является измерительная техника. Так, например, в оптическом диапазоне периодические структуры применяются в качестве чувствительных элементов для измерения температуры, давления, состава вещества и т. д. В настоящей статье рассматривается подход к измерительному контролю комплексной диэлектрической проницаемости жидкостей на основе применения брэгговских структур в СВЧ коаксиальном волноводе.

Для полной информации о диэлектрических свойствах жидкости необходимо знать ее комплексную относительную диэлектрическую проницаемость: б = е'- j&" , включающую вещественную часть ε′ , характеризующую процессы поляризации в веществе, и мнимую – ε′′ , ответственную за потери. Иногда для характеристики потерь вводят тангенс угла диэлектрических потерь tg δ= ε′′ / ε′ .

Измерительный преобразователь в виде брэгговских СВЧ-структур в коаксиальном волноводе (БСВЧСвКВ) предполагает косвенное определение диэлектрических параметров материала по измеренному первичному информационному сигналу, который в данном случае может собой представлять частотную характеристику коэффициента отражения (КО) или передачи (КП) волновода с неоднородностями. Достижение требуемой чувствительности приводит к необходимости заполнения волновода или его части исследуемой средой. В зависимости от ε′ и tg δ исследуемого диэлектрика, ориентировочные значения или диапазон изменения которых считаем известным, можно выделить три класса БСВЧСвКВ:

• I.    Структуры, представляющие собой воздушную коаксиальную линию с периодическими нерегулярностями во внешнем и/или внутреннем проводнике, а также элементами во внешнем проводнике, позволяющим проникать исследуемой среде в чувствительную область датчика. Примером мо

  © Фархутдинов Р.В. и др., 2019

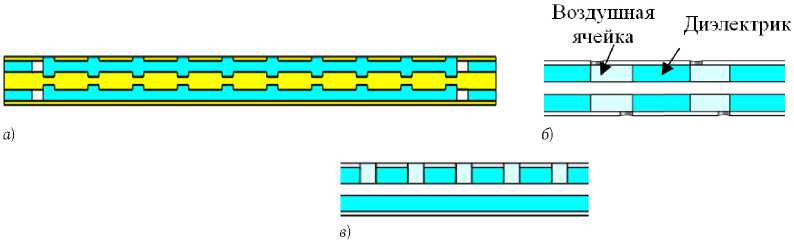
Рис. 1. Конфигурации коаксиальных брэгговских СВЧ-структур в коаксиальном волноводе

жет служить структура с нерегулярностями в виде ступенчатого изменения диаметра внутреннего проводника и отверстиями определенной формы во внешнем проводнике (рис. 1, а ).

• II.    Структуры, реализованные в волноводе с диэлектриком и характеризующиеся введением исследуемой среды в периодически расположенные воздушные ячейки, которые представляют собой отрезки волновода без диэлектрика и включающие элементы во внешнем проводнике для введения и выведения среды (рис. 1, б ).

• III.    Структуры , отличающиеся от предыдущих тем, что измерительная ячейка заполняет только определенную область в поперечном сечении волновода. Примером может служить отверстия цилиндрической формы, образованные полостью во внутреннем диэлектрике волновода и внешнем проводнике и представляющие собой периодические неоднородности в волноводе (рис. 1, в ).

В структурах, отнесенных ко второму и третьему классам, также могут присутствовать нерегулярности проводников. БСВЧСвКВ, отнесенные к первому классу обладает высокой чувствительностью в силу полного заполнения области волновода, но не пригодна для измерения жидкостей с большим значением tg 5 (более 0,1). Второй и третий класс, наоборот, способны измерять s' и s" сильно поглощающих сред, но обладает меньшей чувствительностью.

Типичная частотная характеристика КО периодической СВЧ-структуры представлена на рис. 2, там же указаны названия основных характерных элементов. Периодичность в расположении частотных полос заграждения приводит к появлению понятий вторая, третья полосы заграждения и т. д.

При разработке преобразовательных элементов на основе БСВЧСвКВ необходимо рассмотреть вопросы построения модели измерения и теоретического анализа неопределенностей (погрешностей) измерения диэлектрических параметров

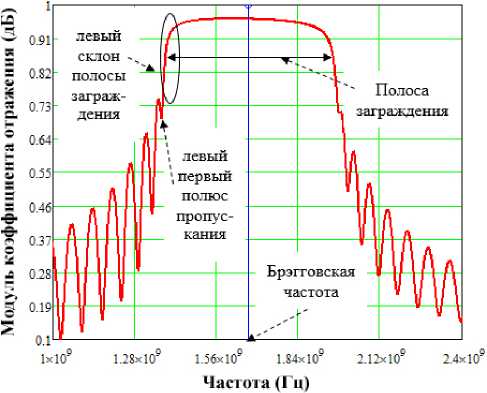
Рис. 2. Типичная частотная характеристика периодической СВЧ-структуры

жидких сред. Под моделью измерений понимается правило или функциональная зависимость между вектором измеряемых величин У и вектором входных величин X , от которых зависит У . С математической точки зрения модель измерений в общем виде можно охарактеризовать выражением:

y ( y , х ) = 0

В качестве выходных (измеряемых) величин примем s' и s'' . Входными величинами, исходя из схемы, будут выступать:

• •    значения модуля |г( f i )| и фазы arg( Г ( f )) КО и модуля | к ( f i )| и фазы arg( K ( f i )) КП на заданных частотах f i , i = 1... M , где М - количество частотных точек;

• •    электрические и геометрические параметры чувствительного элемента A j , j = 1... N , где N -количество параметров;

• •    результаты измерений вспомогательных средств измерений A j , j = 1 ^ K , где K - количество средств измерений.

Составление выражения (1) для измерения s' и s'' жидкости в явной форме является сложной задачей, решение которой даже если и возможно,

в )

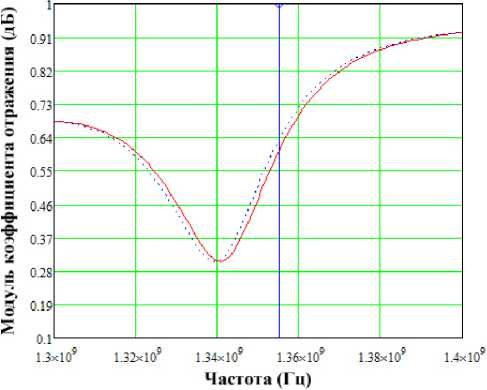
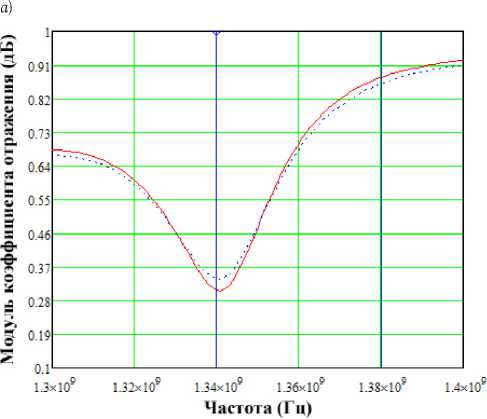
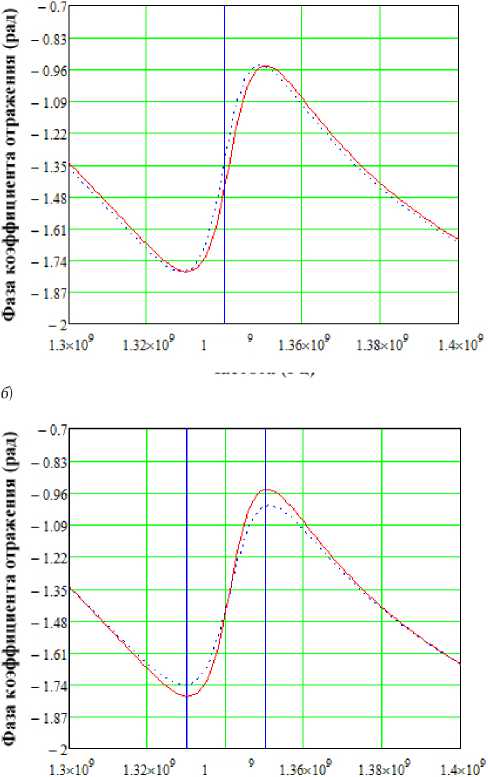
Рис. 3. К анализу чувствительности определения ε′ по отношению к модулю ( а ) и фазе ( б ) КО и ε′ _r ′ по отношению к модулю ( в ) и фазе ( г ) коэффициента отражения

1.34x10

Частота (Гц)

г )

134x10г

Частот» (Гц)

может характеризоваться степенью приближения, не допускающей точность представления результата, необходимой в конкретной измерительной задаче. Поэтому целесообразнее представить выражение (1) как уравнение, результатом решения которого будут значения величин ε′ и ε′′ . Анализ схожих по свойствам измерительных задач СВЧ-диэлектрометрии показывает, что данные уравнения принадлежат классу нелинейных трансцендентных уравнений или системе таких уравнений. В основе их лежат функциональные зависимости комплексных коэффициентов рассеяния СВЧ-четырехполюсников от нескольких переменных, включая и диэлектрические параметры ε′ и ε′′ . Отсюда следует, что основной задачей построения модели измерений является нахождение адекватных данной измерительной задаче выражений для нахождения Γ , K , arg( Γ ) и arg( K ). Такое выражение в дальнейшем будем называть математической моделью БСВЧСвКВ.

Математическая модель БСВЧСвКВ помимо использования в модели измерений диэлектрических параметров, также позволяет оценить особенности влияния параметров БСВЧСвКВ на метрологические характеристики средства измерения на ее основе. В статье предложено использование приложения классических матриц передачи к анализу характеристик БСВЧСвКВ в силу определенных особенностей данного метода, отличающих их от волновых матриц передачи. К ним в первую очередь следует отнести простоту учета в модели эквивалентных схем для неоднородностей. Классическая матрица передачи или ABCD-матрица связывает полные токи и полные напряжения на выводах четырехполюсника (которые в случае ТЕМ-волны в коаксиальном волноводе являются физически существующие, а не фиктивные), что облегчает преобразования матриц сопротивления Z и проводимости Y в ABCD-матрицу и обратно. Прямая связь с матрицами Z и Y по- зволяет вводить в каскадное соединение элементы, представленные своими эквивалентными цепями сопротивления или проводимости. Общая ABCD-матрица БСВЧСвКВ будет определяться каскадным перемножением матриц регулярных участков и неоднородностей.

Обладая функциональной зависимостью КО БСВЧСвКВ от ε′ и ε′′ можно оценить метрологические характеристики средств измерительного контроля. Основная цель вычислительного эксперимента состояла в определении чувствительности измерения ε′ и ε′′ и оценке погрешности измерения по априорным данным неопределенностей измерения комплексного КО, задаваемых как зависимости от уровня измеряемого КО. Проведенный анализ показал, что максимальная чувствительность при измерении ε′ исходя из модуля КО, проявляется на частоте, соответствующей середине левого склона полосы заграждения, исходя из фазы – на частоте первого полюса пропускания. Сказанное подтверждается графиками на рис. 3, а и рис. 3, б , где показаны частотные зависимости модуля и фазы КО для случая двух близких значений ε′ и с помощью вертикальных линий указаны частоты с максимальной чувствительностью.

Из графиков также можно наблюдать, что для частоты на середине склона характерна низкая чувствительность по фазе КО, а для частоты полюса пропускания – по модулю КО. Отсюда следует, что целесообразнее производить измерения на обеих частотах, их близость означает незначительную разницу диэлектрической проницаемости, поэтому можно принять ее равной для обеих частот.

Аналогичные результаты были получены и для ε′′, которые показали максимальную чувствительность по отношению к модулю КО на частоте первого полюса пропускания и начала левого склона (рис. 3, в), а по отношению к фазе КО – на середине левого склона полосы заграждения и середине правого склона первой побочной полосы заграждения (рис. 3, г). Такая ситуация прямо противоположна вышеописанному случаю измерения ε′, следовательно, измерение необходимо проводить в перечисленных четырех частотах: середина правого склона первой побочной полосы заграждения, полюс пропускания, середина левого склона полосы заграждения и начало левого склона полосы заграждения.

На следующем этапе рассматривались теоретические оценки погрешностей измерения ε′ и ε′′ на основе априорной информации о неопределенности измерения модуля и фазы коэффициента отражения БСВЧСвКВ и ранее сделанных предположений о наиболее чувствительных участках частотной характеристики. Были рассмотрены погрешности при использовании БСВЧвКВ на воздушной коаксиальной линии и БСВЧСвКВ с диэлектрическими слоями. Для БСВЧСвКВ на воздушной коаксиальной линии в табл. 1 представлены абсолютные погрешности Δε′ и Δε′′ для различных ε′ и одного значения tg δ= 0,01 и параметров структуры: r ₁ = 1,5 мм, r ₂ = 2,5 мм, L ₁ = L ₂ = 5 мм, R ₁ = R ₂ = 5 мм, количество элементарных ячеек – 10.

При увеличении тангенса угла потерь измеряемого образца для улучшения метрологических характеристик следует применять структуры с частичным заполнением внутреннего пространства волновода. Был проведен анализ погрешности для структуры, изображенной на рис. 1, б , с диэлектрическими слоями в виде фторопласта, результат которого показан в табл. 2.

На следующем этапе была рассмотрена конфигурация с добавлением к предыдущей ступенчатых нерегулярностей внутреннего проводника при r ₁ = 1,5 мм и исследовано ее поведение при различных значениях r ₂ для жидкости с ε′ = 5 и ε′′ =0,5. Результаты сведены в табл. 3.

Анализируя данные в табл. 3 и сравнивая с данными из табл. 2. можно сделать вывод, что введение проводящих нерегулярностей позволяет уменьшить погрешности почти в 10 раз.

Проведено экспериментальное моделирование БСВЧСвКВ как чувствительных элементов для исследования диэлектрических свойств жидкостей на примере автомобильных топлив различных марок. По причине слабого поглощения

Таблица 1

Абсолютные погрешности измерения ε′ и ε′′ для БСВЧвКВ на воздушной коаксиальной линии

tg δ= 0,01	ε′
	5	20	50
Δε′	0,0022	0,012	0,05
Δε′′	0,0017	0,007	0,024

Таблица 2

Абсолютные погрешности измерения ε′ и ε′′ для БСВЧСвКВ с диэлектрическими слоями

tg δ= 0,1	ε′
	5	20	50
Δε′	0,5	0,8	2,5
Δε′′	0,18	0,4	2,3

Таблица 3

Абсолютные погрешности измерения ε′ _r и ε′ _r ′ для БСВЧСвКВ с диэлектрическими и проводящими нерегулярностями

r 2 (мм)	0,5	2,5	3	4,5
Δε′	0,5	0,047	0,065	0,08
Δε′′	0,04	0,021	0,038	0,065

а )

б )

Рис. 4. Внешний вид чувствительного элемента ( а ) и измерительной установки ( б ) для определения диэлектрических параметров автомобильных топлив

Частота (Гц)                                                        Частота (Гц)

а )                                                                                            б )

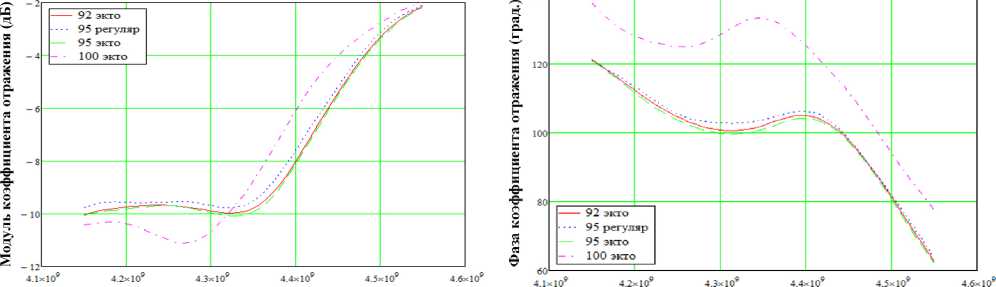
Рис. 5. Результаты измерений автомобильных топлив: модуль коэффициента отражения ( а ), фаза коэффициента отражения ( б )

данными жидкостями электромагнитных волн СВЧ-диапазона, то есть обладающими низким значением tg δ , был выбран вариант чувствительного элемента в виде воздушной коаксиальной линии с периодическим ступенчатым возмущением внутреннего проводника. Внешний вид сенсора показаны на рис. 4, а . В качестве измеряемых образцов выступали бензины марок «92 экто», «95 регуляр», бензин «95 экто», бензин «100 экто». На рис. 5 показаны измеренные частотные характеристики КО БСВЧСвКВ для всех вариантов образцов.

Как можно наблюдать из графиков наиболее близки друг к другу результаты для бензинов «92экто» и «95экто», что говорит о большем влиянии на диэлектрические свойства присадок.

Таблица 4

Результаты измерения значений ε′ и ε′′ для различных марок бензина

Марки бензина	ε′	ε′′
92 экто	2,146	0,023
95 экто	2,158	0,022
95 регуляр	2,197	0,029
100 экто	2,283	0,017

Заключение

Основным результатом является создание возможности применения брэгговских СВЧ-структур в коаксиальных волноведущих системах в задачах измерительного контроля комплексной диэлектрической проницаемости жидких сред.

В частности, при использовании различных конфигураций брэгговских СВЧ-структур в коаксиальном волноводе в качестве измерительных преобразователей можно достигнуть значений неопределенности измерения Δε′ жидких диэлектриков при значениях ε′ от 1 до 10 и при tg δ от 0 до 0,01 равной ± 0,1 %, при tg δ от 0,01 до 0,1 равной ± 1 %.

Работа выполнена при поддержке Министерства ственных заданий КНИТУ-КАИ № 8.6872.2017/8.9 и науки и высшего образования РФ в рамках государ- № 2.1724.2017/4.6.