Брэгговское согласование при мультиплексировании объемных голограмм

Бюллетень науки и практики / Bulletin of Science and Practice

При записи информации с Брэгговским согласованием происходит восстановление только той страницы записанной информации, волна от которой удовлетворяет условию этого согласования. Важно, что при этом другие голограммы не восстанавливаются, учитывая, что их восстановление не удовлетворяет условию Брэгга. Но необходимо помнить, что согласование по Брэггу можно рассматривать только применительно к толстослойным средам, т. е. толстослойным голограммам [1–3].

В основе методов записи мультиплексированных голограмм лежат угловое и по длине волны изменение характеристик процесса записи голограмм, а также кодирование фазы. Перечисленные требования являются обязательными для методов мультиплицирования голограмм на основе Брэгговского сдвига.

При мультиплексировании голограмм необходимо помнить, что при записи голограмм на одной и той же области записывающей среды возможность отличить одну голограмму от другой возникает в следствии того, что каждая отдельная голограмма представляет собой запись интерферометрической картины, полученной как результат сложения двух волн — предметной и опорной, причем запись проводится с обязательно при одной экспозиции [4-6].

Для того, чтобы на приемном устройстве типа ПЗС (прибор с зарядовой связью) не происходило наложение изображений, восстановленных с разных голограмм, очень важно, чтобы выполнялись два требования, или, хотя бы, одно из них:

• -    при восстановлении мультиплицированной голограммы опорный пучок перекрывает обычно несколько голограмм, однако, на ПЗС должно попадать только одно восстановленное изображение, то, которое мы хотим считать с нужной нам голограммы;

• -    опорный пучок падает на участок, на котором записаны несколько голограмм, однако, восстанавливается только одна нужная нам голограмма, т. е. схема восстановления построена

так, что опорный луч как бы обладает способностью отсеивать ненужные изображения. Такая способность к выборке задается с помощью изменения характеристик восстанавливающей волны по отношению к характеристикам записывающей опорной волны. К ним относятся изменения угла падения, фазовых характеристик волны, длины волны и др. Восстановление при других характеристиках приводит к резкому снижению дифракционной эффективности голограммы до пренебрежимо малых значений [7-9].

Целью данной работы является анализ влияния записывающей световой волны на толстослойные среды при мультиплексировании голограмм с использованием согласования по Брэггу.

Согласование по Брэггу при мультиплексировании на толстослойных записывающих средах

Дифракции на плоских решетках и объемных средах сильно отличаются. В случае дифракции на двумерных решетках накладываемые условия менее жесткие на формирование дифракционных максимумов, чем в случае трехмерных, объемных сред. В случае трехмерных решеток условием возникновения дифракционных максимумов является равенство углов падения и дифракции, которые образуют волны с плоскостью объемной решетки. Указанный угол j должен удовлетворять Брэгговскому условию

2 d sin j = l .

Небольшое изменение j или l , при фиксированном значении периода решетки d, что приводит к отклонению от условия Брэгга для дифракционных максимумов, интенсивность света, подвергшегося дифракции, и, как следствие этого, резко падает до пренебрежимо малых значений, часто практически до нулевых величин. Именно данный эффект, определяемый отклонениями от условия Брэгга, и позволяет эффективно осуществлять выборку с помощью изменения угла освещения или изменения длина падающего излучения [10-11].

Наиболее эффективной была бы записывающая среда, представляющая собой объемную решетку, показатель преломления которой меняется скачком только в определенных плоскостях, а в остальных областях решетки оставался бы неизменным. Подобная объемная решетка вела бы себе, по сути, как плоская решетка штрихового типа. Однако, в реальной ситуации на распределение показателя преломления в объемной среде влияет пересечение двух волн плоского типа, а это задает соответствующее распределение показателя преломления в виде синусоиды (Рисунок 1).

Далее рассмотрим более подробно связь между изменением характеристик объемной решетки и падающей световой волны с изменением дифракционной эффективности этой решетки на примере объемных фазовых пропускающих сред.

Рассмотрим две волны плоского типа, имеющие амплитуду равной единице и падающих под углами g ₁ и g ₂ к поверхности среды, на которой ведется запись голограммы, и имеющий исходный показатель преломления равный n. В среде углы распространения волн изменятся и станут равными F 1 и F 2 относительно нормали к поверхности записывающей среды.

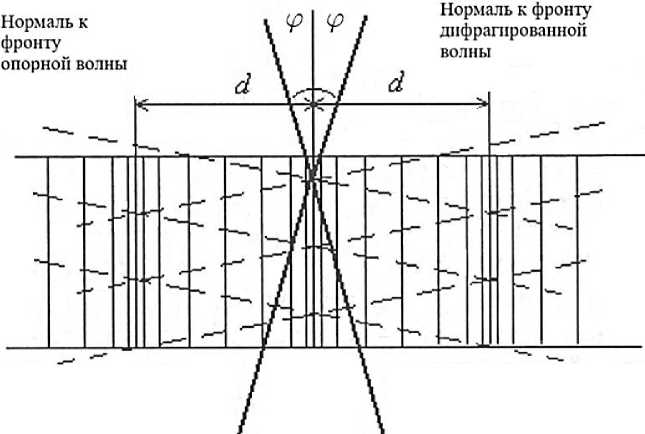
Рисунок 1. Картина, показывающая, как распределяется показатель преломления в объемной среде при сложении двух волн плоского типа

Будем рассматривать взаимодействие указанных двух волн в плоскости yz, причем ось z нормальна к поверхности записывающей среды, а ось y направлена параллельно поверхности среды. В этом случае результирующая амплитуда, в общем случае комплексного вида, имеет следующий вид:

• c(y, z) = exp[- i2p(X1 y + c 1z)] + exp[- i2p(x2y + c 2z)],                               (2)где X = sin Fi /1, a x2 = sin F 2 /l.

Соответственно c_x = cosFj/ l = (1- sin ² F J¹ / ² / 1 , c ₂ = cosF₂/ 1 .

Картина распределения интенсивности в возникающей интерференционной картине рассчитывается в виде произведения двух комплексно-сопряженных величин- в нашем случае амплитуд волны.

• I :    bb* = 2 + 2cos2 p [( x - x ₂) y + ( c_l - c ₂) z ].                                      ⁽³⁾

Учитывая ранее поставленные условия, можно понять, что второе слагаемое в аргументе косинуса представляет собой постоянную величину, которой можно пренебречь. В конечном виде частота интерференционной картины в направлении оси y имеет вид:

h_y = 1/ d cos q = x - x ₂ = (sinF,- sinF₂)/ 1 ,                                    ⁽⁴⁾

где d — расстояние между соседними интерференционными максимумами в распределении интенсивности в интерференционной картине. Из Рисунке 1 видно, что q = (F i + F₂)/2. Это соотношение определяет связь между d, l , которое представляет собой длину волны в рассматриваемой среде, и задает направление волн в среде.

Случай, когда F 1 = - F ₂ и q = 0 представлен на Рисунке 1. При условии, что F 1 = 0 , следует, что h = 1/ d = 2sin j / 1 и 2 d sin j = l .

Объемная решетка, которую мы рассматриваем, формируется за счет суперпозиции двух плоских волн, т. е. голограмма имеет синусоидальное распределение интенсивности.

Рассмотрение именно такого типа решетки оправдано, так как решетку любого другого, несинусоидального типа можно свести к сумме синусоидальных решеток. Иными словами, волну с фронтом любой сложности можно выразить через суммарное действие волновых фронтов простых плоских волн.

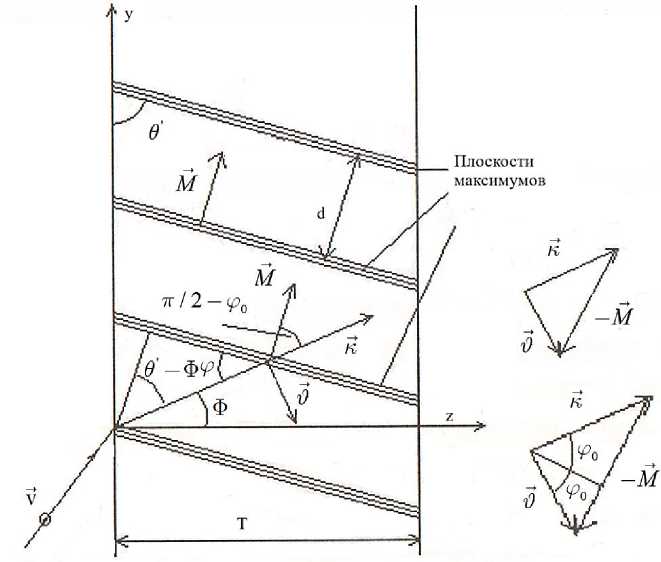
Голограмму, получившуюся при записи на объемной среде, т. е. после экспонирования и проявления, можно описать с. помощью вектора объемной решетки M = | М | = 2 p / d , которая получается при суперпозиции предметной и опорной волн с волновыми векторами k и J (Рисунок 2).

/-о                              Z=T

Рисунок 2. Распределение волновых векторов в объемной среде при суперпозиции двух плоских волн

Распределение показателя преломления, сформированного в записывающей среде, подчиняется синусоидальному закону в направлении вектора решетки M = |М| , который лежит в плоскости yz и направлен по нормали к плоскостям постоянной фазы. Волна света, в данном случае плоская и монохроматическая, падающая на голограмму при ее восстановлении, внутри голограммы распространяется в направлении, задаваемым волновым вектором k , направленный под углом F к оси z. Направление распространения волны после дифракции задается значением вектора J. Для случая, когда F 1 = F 2 = j вектор M направлен параллельно поверхности голограммы, а k = |k| = a,kz / a = Jz I a = cosj 0 . Оценка дифракционной эффективности фазовых голограмм пропускающего типа может быть оценена введением параметров t и e , которые связаны с величинами d , представляющим собой отличие угла распространения восстанавливающей волны от брэгговского угла, параметром a , толщиной слоя l и nl , представляющим собой приращение показателя преломления, l в = nl - длиной волны света, падающего на рассматриваемый слой среды, j 0 -брэгговским углом.

t = Ja l sinj0

e = p nl /1 Ocosj 0

Для оценки дифракционной эффективности z для начала будем считать, что свет падает на поверхность среды под брэгговским углом, т. е. J = 0 и t = 01 В этом случае z = 1, при условии, что e = 1, т. е. e = pnl /10 cosj 0 = p /2 или nl / cos = 10 /2.

Левая сторона соотношения (7) представляет собой приращение оптической длины пути падающей на среду световой волны, которое наблюдалось бы в случае, если бы среднее значение изменения показателя преломления было равно n 1 [12]. Можно сделать вывод, что, если в формировании голограммы участвует только изменение показателя преломления среды, то даже пренебрежительно малые изменения показателя преломления приводят к тому, что дифракционная эффективность z достигает величины 1, но, при условии, что l достаточно велико, чтобы выполнялось соотношение (7).

Если среднее изменение показателя преломления равно n = 10 ³, то значение толщины среды равно l = 0,2 - 0,4 мм, а при n = 10 2 толщина среды достигает нескольких мкм для того, чтобы достичь дифракционной эффективности равной 100%.

Выводы

Выполнен анализ влияния согласования по Брэггу на запись и восстановление мультиплицированных голограмм на толстых средах. Показано, что для того, чтобы на приемном устройстве типа ПЗС (прибор с зарядовой связью) не происходило наложение изображений, восстановленных с разных голограмм, очень важно, чтобы выполнялись два требования, или, хотя бы, одно из них:

• -    при восстановлении мультиплицированной голограммы опорный пучок перекрывает обычно несколько голограмм, однако, на ПЗС должно попадать только одно восстановленное изображение, то, которое мы хотим считать с нужной нам голограммы;

• -    опорный пучок падает на участок, на котором записаны несколько голограмм, однако, восстанавливается только одна нужная нам голограмма, т. е. схема восстановления построена так, что опорный луч как бы обладает способностью отсеивать ненужные изображения. Такая способность к выборке задается с помощью изменения характеристик восстанавливающей волны по отношению к характеристикам записывающей опорной волны. К ним относятся изменения угла падения, фазовых характеристик волны, длины волны и др. Восстановление при других характеристиках приводит к резкому снижению дифракционной эффективности голограммы до пренебрежимо малых значений.