Быстрая обработка аэрокосмических изображений, использующая минимальные кубатурные формулы

Рассмотрим плоское изображение f ( x , y ), где f –яр-кость, 0 <  x , y <  1, f ( x , y ) e L ². Это может быть высок о качественная фотография земной поверхности, полученная с борта авиационных или космических носителей. Считаем, что f ( x , у ) – периодическая функция двух переменных с периодом 1 по каждой ичто f ( x , у ) можетбыть разложена в абсолютно сходящийся ряд Фурье:

Коэффициенты a _{m , n} образуют двумерный спектр Фурье функции f ( x , у ).

При двумерном дискретном преобразовании Фурье устанавливается взаимно однозначное соответствие между значениями функцииfx, у)в узлах Xj, yl, 0 < j, l < N -1 и множеством чисел Am,n, 0 < m, n < N -1, так что тригонометрический полином f (x.y)-3 am, ne '•■'"-* '-',3 am.1 <",(1)

m,n am.n = J J f (x,' ) e-2”(xm*'n)dxd'•(2)

N - 1

T(x,y)- 3 Amne '('-■ *""'(3)

• m, n - 0

восстанавливает функцию f ( x , у ) в узлах, т. е. T ( x j , ' i ) - f ( x j , ' i ) , 0 <  j , l <  N - 1. при этом число

A _{m , n} ,0 ≤ m , n ≤ N - 1, есть кубатурная сумма в кубатур-ной формуле

N - 1

Q ( m , n ) = 1 2 ∑ f ( x j , y l ) e ^{- 2 π i ( xjm + yln )}= A m , n ,(4) N j , l = 0

• т. е. приближенное значение коэффициента Фурье a_{m, n} ряда Фурье (1) отфункции f ( x , y ) с заданной тригонометрической степенью d ≥ 1 . Последнее означает, что формула (4) точна для всех функций вида f ( z , w ) = z ^α w ^β ,где α , β ∈ Z , I α I + I β ≤ d и не точна хотя бы для одной такой функции с I α+ I β I = d + 1 [1].

Важной проблемой теории кубатурных формул высокой тригонометрической точности является построение минимальных кубатурных формул, т. е. таких, у которых число узлов при данном d было бы минимальным [1].

Фотографическое изображение может быть отсканировано с помощью некоторого устройства, например, настольного сканера, который считывает значения яркости f ( х , у ) в узлах прямоугольной решетки x = x_j , y= y_l , 0 ≤ j ≤ N ₁ - 1,0 ≤ l ≤ N ₂ - 1, N ₁ и N ₂– количество отсчетов по х ипо у . В этом случае f ( х , у ) = f ( x_j , y_l ) = f ( j , l ). Классическим методом (КМ) вычисления спектра двумерной дискретной функции является применение двумерного дискретного преобразования Фурье (ДДПФ) по квадратной решетке N ₁ = N ₂ = N [2]:

1 ^{N - 1}2 π ijn 1 ^{N - 1} 2 π ilm

A n , m = _N ∑ _{j = 0} [exp( _N ) _N ∑ _{l = 0} f ( j , l )exp( _N )] . (4)

При КМ вначале выполняется одномерное преобразование Фурье по столбцам, а затем результат подвергается одномерному преобразованию по строкам (или наоборот, вначале по строкам, а затем по столбцам). Общее число операций сложения и умножения составляет N ⁴ . Вычисление приближенных значений коэффициентов Фурье по формуле (4) в КМ проводится на основе декартова произведения двух одномерных квадратурных формул с N узлами, кубатурная формула имеет N ² узлов, её тригонометрическая степень d = N - 1 (рис. 1). Квадратная решетка показана на рис. 1, а . Существуют кубатур-ные формулы такой же степени d , но имеющие значительно меньшее число узлов [3].

Для ускорения вычислений при КМ применяются быстрые алгоритмы, чаще всего алгоритм Кули–Тьюки [2]. Его особенностью является выбор числа отсчетов из условия N= 2 ^M , М – натуральное число. Преимущество такого выбора состоит в том, что значения тригонометрических функций достаточно вычислять 2 М раз, поскольку они периодически повторяются. Кроме того, вычисления можно проводить по рекуррентным формулам. Число операций сложения и умножения при нахождении коэффициентов Фурье одной строки или столбца изображения размерностью N × N пикселов с применением алгоритма Кули–Тьюки равно N ⋅ log₂ N . Проводя преобразование по каждой из N строк изображения и повторяя этот процесс по каждому из столбцов, получаем в итоге 2 N ² ⋅ log₂ N операций.

Важное применение классического метода ДДПФ – глобальная фильтрация изображений. Пусть, например, изображение искажено (расфокусировано) некоторой линейной системой (например, фотографическим объективом) сфункциейрассеянияточкиh(x, y). Возьмемзна-чения h(x, y) в тех же узлах квадратной решетки: x = xj, y =yl, j,l=0,N-1,что и для изображения f(x, y), т. е. будем рассматривать функцию h(xj, yl) =h(j, l). ДДПФ от h(j, l) является частотным коэффициентом передачи линейной системы:

1 ^{N - 1}2 π ijn 1 ^{N - 1}             2 π ilm

B n , m = _N ∑ _{j = 0} [exp( _N ) _N ∑ _{l = 0} h ( j , l )exp( _N )].

Спектр искаженного изображения равен C_{m , n} = A_{m , n} B_{m , n} . Для восстановления изображения выполним инверсную фильтрацию и найдем оценку A _m ^* _{, n} = C _{m , n} / B _{m , n} . Здесь предполагается, что обратная задача является корректной, в противном случае следует использовать регуляризацию решения. Далее выполняется обратное ДДПФ:

^{N - 1}       - 2 π ijm ^{N - 1}          - 2 π iln

f ^*( i , l ) = ∑ [exp(         ) ∑ A m ^* , n exp( )].

m = 0 N n = 0 N

Минимальные кубатурные формулы, точно интегрирующие тригонометрические многочлены степени не большей, чем d , могутиметь различный вид. Имея в виду, что ниже будет использован алгоритм быстрого преобразования Фурье по Кули–Тьюки, положим число узлов минимальной кубатурной формулы равным 2 ^М . При этом d должно быть нечетным; пусть d = 2 k + 1, минимальное число узлов составляет N ^* = 2 ( k + 1 ) ² . Сравним число узлов такой минимальной кубатурной формулы и КМ одинаковой тригонометрической степени d . Для КМ имеем d = N – 1. Таким образом, при КМ число узлов N ² = 4( k + 1)², т. е. в два раза больше.

Всоответствиис[4] при d= 2 k+ 1 выберем в качестве узлов минимальной кубатурной формулы точки с координатами

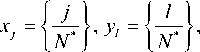
N ^* = 2( k + 1)², l = (2 k + 1) j , 0 ≤ j ≤ N ^* - 1, (5) фигурные скобки {} означаютдробную часть числа. Таким образом, координаты узлов зависят от одного индек-са j . Решетка, соответствующая (5) (рис. 1, б ), содержит узлы, расположенные вдоль параллельных прямых и достаточно равномерно покрывает изображение. Узлы отмечены черными точками. Параллельные линии, проходящие через узлы решетки (на рис. 1, б показана одна из них), представляют собой некоторые отрезки прямой. Так как f ( x , у ) – периодическая функция двух переменных с периодом 1 по каждой, то отрезки можно выстроить вдоль одной прямой, на которую укладываются все узлы, т. е. сформировать вектор f ( j ). При работе с этим вектором можно применять алгоритм одномерного дискретного преобразования Фурье. Используя одномерное преобразование Фурье, мы обходим каждый узел один раз, а при КМ– два раза. Совокупность узлов, соответствующую формуле (5), далее будем называть наклонной решеткой . Для ввода фотоизображений в компьютер по наклонной решетке понадобится специальный сканер.

Прямое и обратное преобразование Фурье отнаклон-ной решетки вычисляются по обычным формулами одномерного преобразования. Вместо коэффициента А_n,m получаем А_n :

• 1         /2 п j

A ■ ' Г j =0 f ( j ^)exp( - '^

обратное преобразование дает значение яркости в j- м узле:

• ¹     г^{- 2} ™ j

f ⁽ j ) = L A n ^ex p ⁽ _v» ).

n = 0           '

При построении изображения f ( j , l ) по вектору f ( j ) координата узла l задается как l = j (2 k + 1).

Определим погрешности вычисления коэффициентов А_n,m по КМ (расстановка узлов по квадратной решетке) и коэффициентов А_n по наклонной решетке в сравнении с точными коэффициентами а_n,m , вычисляемыми по формуле (2). Используется преобразование Фурье без убыстряющих алгоритмов, число узлов подбирается таким, чтобы для КМ и наклонной решетки оно было приблизительно одинаковым.

Рассмотрим тестовое изображение «шахматное поле», содержащее 5 белыхи4 черных квадрата, размер стороны квадрата равен 1/3 размера стороны всего поля (рис. 1, в ). Белому полю присваивается значение 0, черному 1. В первом столбце таблицы приведено число узлов N ² квадратной решетки, во втором – значения среднеквадратичного отклонения S коэффициентов Фурье для КМ отточных значений, в третьем столбце – число узлов N ^* для наклонной решетки и в четвертом – значения среднеквадратичного отклонения S коэффициентов Фурье для наклонной решетки.

Анализ данных таблицы показывает, что значения среднеквадратичного отклонения коэффициентов Фурье для наклонной решетки приблизительно такие же, как для квадратной решетки; тенденция к уменьшению погрешности с ростом числа узлов более стабильна, чем при КМ.

Наклонная решетка была использована при восстановлении расфокусированного изображения путем инверсной фильтрации (рис. 2). Вычислялся спектр исходного изображения A_n , коэффициентпередачи линейной системы B_n задавался в виде

Bn = —1^. 1 + an²

Спектр расфокусированного изображения имеетвид C n = A n ■ B n , оценка восстановленного спектра при инверсной фильтрации равна A n = C n / B n . На рис. 2, а приведено исходное изображение, полученное при дистанционном зондировании Земли с космического носителя, на рис. 2, б – расфокусированное изображение. На рис. 3 показаны действительная часть одномерного спектра исходного изображения ( а ), мнимая часть ( б ) и коэффи-циентпередачи линейной системы ( в ). Число узлов при обработке составило 32 768, что соответствует k = 127 и d = 255. Если использовать классический метод с квадратной решеткой, то число узлов составило бы 65 576. При обработке изображений (см. рис. 2) использовался одномерный алгоритм Кули–Тьюки, число операций сложения и умножения 491 520. Если использовать КМ и дву-

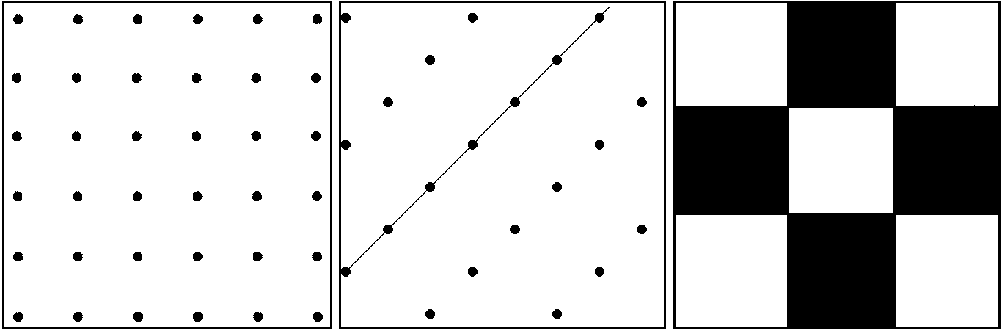
аб   в

Рис. 1. Квадратная решетка ( а ); наклонная решетка при k = 1 ( б ); тестовое изображение ( в )

Погрешность при вычислении коэффициентов Фурье

Классический метод Наклонная решетка N2 S N* S 441 0,010 412 450 0,005 406 529 0,003 485 512 0,005 285 625 0,003 345 648 0,004 123 729 0,007 225 722 0,004 055 841 0,002 487 882 0,003 278 961 0,002 407 968 0,003 236 1089 0,005 387 1058 0,003 032 1225 0,001 888 1250 0,002 660 1369 0,001 837 1352 0,002 511 1521 0,004 214 1568 0,002 236 1681 0,001 496 1682 0,002 124 мерный алгоритм Кули–Тьки, то число операций составило бы 1 048 576.

В этом примере изображение восстановилось с точностью до машинной погрешности.