Calculating lateral deflection of plates subjected to heterogeneous forces of inertia using a variation-difference method
Автор: Sabirov R.A.
Журнал: Сибирский аэрокосмический журнал @vestnik-sibsau
Рубрика: Математика, механика, информатика
Статья в выпуске: 2 т.17, 2016 года.
Бесплатный доступ
The deformation of plates is reduced to the generalized problem of eigenvalues based on the stability criterion, which establishes equilibrium in the mechanical system. A method for calculating stability for thin plates under inertia loads exerting force on the basal plane is proposed. Having a differential formulation of the problem, the matrices are formed. The first is a stiffness matrix: it is based on Marie-Sophie Germain’s biharmonic equation. The second matrix represents the change of internal stresses or internal forces in the plate. The stiffness matrix is always symmetric and positive definite for the fixed plate. The matrix of the internal forces in the approximation of derivatives of functions under central differences, from the action of inertial forces can be asymmetric with respect to the main diagonal, can also degenerate and rows of this matrix is the feature of inertia loads. The finite difference method allows us to form a system of large dimensional equations. However, difficulties may arise at the free edges and corners of the plate, which complicates the calculation procedure. Therefore, a transition from the differential formulation of the problem to an integral formulation discretization with variational-difference method is performed. In this case a second row of nodes is not formed during the formation of the stiffness matrix at the free edge. The matrix of the internal forces is always symmetric; it can be ill-conditioned, however, this factor does not affect the problem of determining eigenvalues. Scientific literature provides many theoretical studies and solutions to practical tasks of calculating the stability of structures, including the calculation of longitudinal-transverse bending of thin plates. However, this is a task that has positively certain operators. We have conducted a research of the application of the variational-difference method for calculating the stability of structures. The differential formulation of the boundary value problem is transformed into a variational formulation; the stability criterion is solved; the issue of approximating differential operators for discrete problems with a finite number of variables is addressed in the paper. The paper also describes a developed set of algorithms for the Maple mathematical system and a compilation of calculating programs. Examples of the calculation are considered. We have studied a plate that is rigidly secured at one side while the other three sides are left unfixed. Values of the critical accelerations have been obtained. Problems are assigned to the generalized problem of eigenvalues in which the acceleration parameter, such as the parameter of load, is the only unknown property. Paper objective: the development of a method for calculating inertia loads on plates.
Calculating load of plates, stability, variation and differential method
Короткий адрес: https://sciup.org/148177569
IDR: 148177569 | УДК: 539.3
Текст научной статьи Calculating lateral deflection of plates subjected to heterogeneous forces of inertia using a variation-difference method
Introduction . Thin plate elements used in naval and aeronautical structures are subjected to normal and shear forces acting in the plane of the plates [1]. The problem of stability is paramount for the design of vehicles subjected to stress during high speeds and acceleration such as missiles, supersonic aircraft [2]. Among the possible application of the calculation methods is the design of industrial products (high speed multifunctional centrifuges, catapults, jet sledges, banners, thin-walled structures in the form of vertical cantilever plates, stressed by their own weight, etc.). Therefore, we can speak about the relevance of the considered problem. In relation to the calculation of stability of structure plates to the action of acceleration let us consider the classical differential formulation for longitudinal-transverse bending of an isotropic plate in the Cartesian coordinate system [3–7]. Differential formulation is represented by a homogeneous linearized equation of sustainability
Гб 4 w б 4 w б 4 w
D А 4 + 2 А 2?! 2 + А 4
^ б x б x б у б у
—
qz
б 2 w б 2 w _ „ б2w
= N, —у + Nv —у + 2 S™--- x бx2 у бу 2 xy бx бу
in which: D = Eh3/12(1 — ц2) is cylindrical stiffness; E is Young’s Modulus; ц is Poisson’s Ratio; h is the thickness of the plate; w = w(x, у) is the deflection function; qz (x, у) = 0 is a load normal to the surface of the plate. In this paper, equation (1) membrane forces N , N , S arise from the action of inertial loads: x y xy qx (x, у) = hX, qy (x,у) = hY, where volume forces are equal X = pax , Y = pay . These forces depend on material density p and acceleration ax, ay in the directions of the coordinate axes Ox respectively. Thus, exerting external loads on the plate must be uniform, i. e Nx = Nx (x, у) , Ny = Ny (x, у), and Sxy = Sxy (x, у) to vary in proportion to the acceleration.
With finite difference approximations of the differential equation (1) and considering only free loose sides and corners of the plate there arises a algorithmic challenges associated with the exception of the second number of edge nodes. Another feature is that the central approximation by finite differences for the second derivatives of the functions of the deflections in the right part of (1) gives an asymmetric matrix of the internal forces, which complicates the solution of eigenvalues of the discrete boundary value problem. This fact was revealed by the formation of the corresponding matrices of longitudinal-transverse bending of rods [8]. It is therefore advisable to apply a variational-difference method based on total energy principles for the calculation of plates at stability from the action of inertial forces on the action of non-uniform loads.
Problem formulation . The theorems of Lagrange– Dirichlet and Lyapunov covered in the fundamentals of theoretical mechanics [9] formulate the conditions of equilibrium of a mechanical system and explain the criteria of equilibrium positions. For deformable structures these criteria lead to the equations modeling the problem of eigenvalues [1–5; 10–17].
Let эл = эл (w1, w1, ..., w)— (2)
a Lagrange functional of a finite number of variables w 1, w 1, ..., wn , boundary value problem.
The increment of the total potential energy of the deformation variations for the retention w 1 +5 w 1 , w 2 +5 w 2, ..., w n +5 w n of members no higher than the second order is
АЭЛ = Эл(wi +5wi,w2 +5w2, ...,wn +5wn)-
- Э л ( W 1 , w 2 , ..., W n ) = 5 Э л +5 2 Э л /2.
Here the first and second variations of (2) are respectively equal to:
5Эл = (aЭл / a Wk )5 Wk,(4)
52эл = (а 2Эл / a wk awl )5 wk 5 wl,(5)
with summation over repeated indices: k = 1, 2, ..., n , l = 1, 2, ..., n .
For any state of equilibrium 5 Эл = 0 [10]. In problems of sustainability the nature of equilibrium is judged by the sign of the second variation of the functional: the equilibrium is stable if 5 2 Эл > 0, for all admissible virtual displacements; the equilibrium is unstable if at least one admissible virtual displacement 5 2 Эл < 0 . But first the upper critical load corresponds to the transition from stable equilibrium to unstable configurations. Hence, for this value of the load should be
5 2 Эл = 0 . (6)
We introduce in (5) operators of variation 5 1 and 5 2 . We write (6)
5 2 Э л =5 2 ( 5 1 Э л ( w^w 2 ,..., w n ; 5 1 w ^5 1 w 2 ,..., 5 1 w n ;
5 2 w 1 , 5 2 w 2 ,..., 5 2 w n )) = 0. (7)
The condition (6) with (7) is equivalent to the following equation
{ 5 2 w 1 5 2 w 1 ... 5 2 w 1 } x
functions of the internal forces, dependent in the considered work from option acceleration. The parameter acceleration is the load parameter, which is the only unknown of the characteristic determinant (9); and its value, converting the determinant to zero will correspond to the critical values of the load. The roots of the system of equations (9) determine the eigenvalues, i. e. all critical loads, including the smallest of them.
Solution procedure. Let’s get the coefficients for (9) based on integral formulations. For this purpose the differential equation (1) can be converted to an integral equation [15]. We use the equilibrium equations obtained by a deformation scheme [3]:
a Q x a Q a 2 w a 2 w
"л- ' + Nx(x,y)тт + Ny(x,y)тт + ax ay ax2 ay
Г n z z a2 w . . „
+ [ S xy ( x , y ) + S yx ( x , y )] 7T-T- + q z ( x , y ) = 0, a x a y
_ a M x a H yx -aM^ H
Qx + , Qy z-x + z-x ax ay ay ax
.
On the basis of equations (10) we will formulate the “principle of possible displacements”
JJ
S
a2mx a2Hyx a2Hxy a2My a2 w x^ ++++ N + ax2 axay axay ay2 ax 2
a 2 w a y'
( S xy + S yx ) a-w 5 w ( x , y ) dS = 0,
a x a y
|
X |
a 2 эл a 2 эл a 2 эл a w 1 a w 1 a w 1 a w 2 a w 1 a wn a 2 Э л a 2 Э л a w 1 a w 2 a w 2 a w 2 ... ... ... ... a 2 эл a 2 эл a 2 эл a wn a w 1 a wn a w 2 a wn a wn |
5 1 w 1 5 1 w 1 , (8) 1 I = 0, ... _ 5 1 w 1 _ |
where: M x = D ( ж x + цж y ) , M y = D ( ж y + ц ж x ) , Н х У = = Hyx = ( 1 -ц ) D x xy - bending and twisting moments;
ж
x
a2 w ax2’
ж y
a 2 w a y ,
X xy
a2 w axay ’
эх = a w / a x ,
x
9 y = a w / a y - curvature curve and the angles of rotation;
5 w ( x , y ) - potential movement of the surface of the plate;
differential square dS = dxdy .
To decrease the order of derivatives of the moment
functions in (11), let’s perform the internal conversion of
where the matrix contains the coefficients of the variations of the displacements of equation (7). This system will have a solution different from zero only if the determinant composed of coefficients is equal to zero [12]. The grouping of the coefficients of the independent variations of the displacements gives a zero determinant
components like such
rr a2 m rra Hxy
JJ--- 2 x 5 wdxdy , j j a ^ 5 wdxdy ,
a 2 w_ , , , .
Nx ——5 wdxdy by partial integration. This gives the a x 2
- J (Rx5w - Mx59x ) dy y=0
following variational equation x = a y = b
5 Э л = J J D [ ж x 5 ж x +ц ж x 5 ж y + ж y 5 ж x ) + x =0 y =0
x = a y = b
+ ж y 5 ж y + 2 ( i -ц ) х xy 5x xy ] dxd y - J J q z 5 wdxd y - x =0 y = o
- J ( R y 5 w - M y 59 y ) dx
+ y=0
The coefficients in (9) are functions of the parameters of structural rigidity, the ratio of its size; they also are
x = a
+ ( Hx y+ Hv J5 w yb + (12)
\ xy yx / |x =0 |y =0 v 7
x - a У - b
+ J J ( N x ( x , y ) 9 x 59 x + N y ( x , y ) 9 y 59 y + x -0 y -0
Here, 5 i , i - 1,2 is the operators of variation;
§ i $ x
5 2 5 i w 5 x 2
5 i $ y
5 2 5 i w l y^
5 2 5 iw.
5 i X xy - о о ;
5 x 5 y
x 5 wdy
+ S xy ( x , y )( 9 y 59 x +9 x 59 y ) ) dxdy -
y = b
- J ( N x ( x , У ) 9 x + S xy ( x , У ) 9 y ) x:
y -0
x -0
- f(Syx (x’ y)9x + Ny (x, У)9y )5wdx x-0 y-0
- 0.
Here, R x - Q x + 5 В , 1 5 y , R y - Q y + 5 H yx 1 5 x is the generalized reaction; the symbol 5 is the operator variation. From (12) followed by a Lagrange functional
Э Л - 1 = I J D [ $ 2 + 2 9 $ x $ y + $ 2 +
2 x -0 y -0
x - a y - b
+ 2 (1 -9)x2y ] dxdy - J J qzwdxdy - x-0 y - o
У - b
- J ( R x W - M x 9 x ) dy
У -0
- J ( R y W - M y 9 y ) dx
+
x -0
У -0
5:9Т-55, w / 5 x , 5,-9 =55, w / 5 y is the variation of ix i iy i
curvature and variation of angles of rotation.
Let’s analyze the coefficients for the determinant (9). On the basis of (6) expression (14) we will equate to zero, which will lead to the discrete formulation of the stability problem. Let xv - ( w 1 , w 2, ..., w p ) is the displacement
vector for the p variables, 5 1 iw - ( 5 1 w 1 , 5 1 w 2, ..., 5 1 w p )
and 5 2 iw - ( 5 2 w 1 , 5 2 w 2, ..., 5 2 wp ) are variations of the displacement vector. The coefficients for (9) are calculated by the group members at varying deflections:
r - V 5 I 5 Э л ( iw , 5 1 w , 5 2 w )
C ij - ^ я- I ^
k -1 5 w k ( l -1
5 iwi
5 1 wz 5 2 w k - 0, (15)
, . I x - a i y - b
+ ( Hxy + H yx ) w l x - 0 l y - 0 +
I 1, when k - i , 5— , ,
2 w k - 1
[ 0, when k * i ,
Г1, when l - j , 5— , J , 1 w l - 1
[ 0, when l * j ,
i - 1, 2, ..., p ; j - 1, 2, ..., p .
Here, each coefficient C ij - B j - sA ij according to
(14) contains the characteristics of stiffness Aij and internal efforts Bij ; s is the solution of the identity (9). Multiplying found from (15) the coefficients Cij on the
vector wj , get
+ 1 J у J ( N x ( x , y ) 9 2 + N y ( x , y ) 9 y +
2 x -0 y -0
+ 2 S xy ( x , y ) 9 y 9 x ) dxdy -
C j w j - 0,
this is the wording of the generalized eigenvalues problem
[ B ] { w } - s [ A ] { w } ,
-J [ Syx (x, У )9 x + N (x, y) y 9 y ] wdy-
У11
x = a
- J [Syx (x, У)9x + N(x, У)y 9y ]wdx x0
and its second variation
5 2 Эл - J У J d [5 2 $ x 5 1 $ x + 9 ( 5 2 $ x 5 1 $ y +5 2 $ y 5 1 $ x ) + x -0 y -0
+ 5 2 $ y 5 1 $ y + 2 ( 1 -9 ) 5 2 X xy 5 1 % xy ] dxdy +
+ J У J [Nx (x, y)529x519x + Ny (x, y)529y519y + x-0 y-0
+ S xy ( x , У )( 5 2 9 y 5 1 9 x +5 2 9 x 5 1 9 y )] dxdy . (14)
where [ A ] is the stiffness matrix; let’s call [ B ] the matrix of the internal forces or inertia matrix, { w } - ( w 1 , w 2, ..., wp ) is the private vector for p
variables; s is the eigenvalues of the matrix.
For calculating the internal forces located in the right part of the functional (13), it is necessary to apply the same integral formulation. Internal force in (1) are expressed in terms of displacement u - u ( x , y ), v - v ( x , y ), base layer on the basis of Hooke’s law [6]:
N x -
Eh 5 u 5 v
---т--+ 9 — 1 -Ц 2 L5 x 5 y
Sxy
Eh
2(1 + 9 )
N y -
Eh 5 v 5 u
------r"--+ 9---
1 -9 2 L5 У 5 x
15 u 5 v )
I + I . (5 y 5 x J
The displacement function for (18) can be computed using the equilibrium equations of Saint-Venant equations [7] for plane problems of the elasticity theory:
5 15 u 5 v ) 1 -91 5 2 u 5 2 u I1| ++
5 x (5 x 5 y J 1 + 9(5 x 2 5 y 2
2(1 -9 ) Eh
q x , (19)
8 (8 и 8 v ) 1 -ц( 8 2 v 8 2 v — I 1 I н —г н г 8 у (8 x 8 у ) 1 + ц (8 x 2 8 у2
2(1 -ц ) Eh
q y . (20)
Here we see the unknown functions of displacements u ( x , y ), v ( x , y ). On the basis of (19) and (20) with (18) let’s build an equation with possible external and internal forces. The integration in this equation of internal products of parts for a rectangular area 5 : 0 < x < a and 0 < у < b gives:
the system of resolving equations let’s discuss the application of formulas (22) and (23). Let H = ( и 1 , и 2, ..., ир ) be the displacement vector for the p variables, 5 1 и = ( 5 1 и 1 , 5 1 и 2, ..., 5 1 ир ) and 5 2 и = ( 5 2 и 1 , 5 2 и 2, ..., 5 2 ир ) be the variations of the displacement vector. Then to compute the coefficients of the vector of the right part bi of the system of resolving equations, we will write (22) in the form
– a Lagrange functional
Ф л ( u , v )
E
2(1 -Ц 2 )
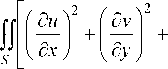
U У -s^-y p^ 8ФЛ ( и , 51 и L. b = 5 1 Ф л ( и , 5 1 и ) = Z — 5----- 5 1 и1 ;
, =1 8 и.
S
+ 2 ц
8 и 8 v 1 -ц (8 и 8 v ^ —— + ^Я — + — I 8 x 8 у 2 (8 у 8 x )
i = 1, 2,
dxdy +
1 1, when l = i , .., p ; 5 1 и , = <
[ 0, when l ^ i .
у = b
Y v) dx dy + J (aXu + Txvv у=0
In order to form the stiffness ai , j of this system of equations, we will form the second variation as a variation of the first, implementing (23) for the discrete tasks:
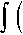
**
a y v + T yxU
– the first variation of the functional
5Ф л
= 5 1 Ф л =
E
(1 -ц 2 )
JJ
S
8 и 85 1 и
8 x 8 x
+
8 v 85 1 v (8 и 85 1 v 8 v 85 1 и )
• H----h Ц |---1---| +
8 у 8 у ( 8 x 8 у 8 у 8 x )
1 -ц( 8 и 8 v V 85, и 85, v
+ —-I —+ — II + I
2 (8 у 8 x )( 8 у 8 x )
+ JJ ( X 5 и + Y 5 v ) dxdy +
S
у = b
+ J (ax5и + Txy5v)dy у=0
h
dxdy +
у = b
=a
J (ау5v + T*,x5и)dx;
=0
– the second variation of the functional
5 2 ф л -б 2 ( 5 , Э л ) -- -E y- JJ (1 -Ц ) 5 _
857 и 85, и
--2--L_ +
8 x 8 x
a ij
8 и ,
p 8Ф л ( - , 5 1 Й , 5 2 Й )
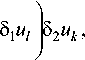
I 1, when k = i , 5 2 ик = 1 , ’
1 0, when к ^ i ,
I 1, when l = j , 5 1 ■ J ~
1 и, = 1
[ 0, when l ^ j ,
i = 1, 2, ..., p ; j = 1, 2, ..., p .
857 v 85, v
■ +---2--L_
8 у 8 у
( 85 7 и 85, v 85, и 857 v ]
+ ц| —2--— + —1--— | +
( 8 x 8 у 8 x 8 у )
1 -ц( 85 2 и 85 2 v V 85 1 и 85 1 v ^
2 (8 у 8 x )( 8 у 8 x )
dxdy . (23)
It is essential to add to (21)–(23) the main boundary conditions: и = и * , v = v * , 5 iu = 5 iu * , 5 i v = 5 i v * , i = 1,2 (known values are marked with (*)). In (21)-(23) a x , т x y , a *, , T * x is specified tension. Thus, to solve the plane problem of the elasticity theory by a variational-difference method we use
5Ф л = 5 1 Ф л = 0 or Ф л ( и , v ) ^ min .
To calculate the displacement и = и ( x , у ), v = v ( x , у ) of the boundary value problem for the purpose of forming
The solution to this system of equations ai j й j = b i produces a displacement vector и j , components of which are calculated the values of the internal efforts Nx ( x , y ), Ny ( x , y ), Sxy ( x , y ); using formulas (18) we assemble the matrix of inertia of the stability problem.
Based on the integral formulation – in fact the problem of the plate buckling and the problem of computing for non-uniform internal forces are resolved by a single scheme – we are able to use the single calculation algorithms.
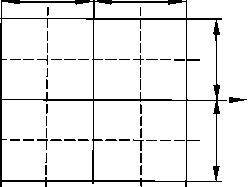
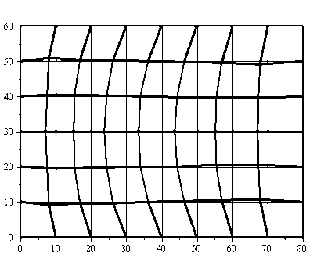
Let’s consider discretization equations (22), (23), (14). Selecting the area of the plate is a rectangular uniform mesh ю.. = { ( x i = i X x , P j = j X y ), i = 0, 1,..., m, j = 0, 1,..., n } on segments [0, lx ] и [0, 1у ]. Here: x = x i and у = y j are the grid nodes; X x = lx / m and X у = 1у / n is the grid step, lx and ly are the dimensions of the plate in the directions of the coordinate axes x and y . Let’s call this grid (fig. 1) the main grid to nodes i , j . Let’s introduce additional grid nodes ^ , p : Ю п = { ( x ^ = X x /2+ i X x , уу = = X y /2 + j X y ), i = 0, 1, ..., m -1, j = 0, 1, ..., n -1 } . Integrals over a region in (22) and (23) and the second integral on the internal forces in (14), are replaced by numerical m -1 n -1
integration JJ ( ) dxdy = ZZ( ) 5 -p (here 5. ■ is the area of integration equal to X x X у nodes in the inner region of the plate) and replace differential operators with finite-difference analogues [18]:
( 55 k u ^ 8 k u i + 1, j + i +8 k u i + i, j -8 k u i , j + i -8 k u i , j
I 5% Xn " 2 X%’
( 58 kv ^ 8 k v i + 1,j +i +8 k v i , j +i -8 k v i +1, j -8 k v i , j
I 5y J, 2Xv
S,n
Г 58 ku + 58 kv ^ _ 8 k u i +1, j +1 +8 k u i , j +1 -8 k u i +1, j -8 k u i , j +
5y 5% L2X
S,n
8kvi+1,j+1 +8kvi+1,j -8kvi,j+1 -8kvi,j 2x%
Further, in the first integral (14) integrating for members containing variations of curvature 8 k ж % and 8k жy replace the summation over the nodes of the main mn draw |J( )dxdy _^^( )Sy and apply the Central
S i _1 j _1
differences
Г5 2 8 kw ) = 8 k w i +1, j - 2 8 k w i,j +8 k w i -1, j
2 _ a,
5%X i,j
Г 5 2 8 kw ) = 8 k w i , j +1 - 2 8 k w i , j +8 k w i , j -1
2 _ л 2
5УX i,j
Here the site of integration S ij is equal to: X % X y - in the internal nodes the area of the plate; X % X y /2 are the nodes located at the contour; X % X y /4 are the nodes located in the corners of the plate.
The curvature of the torsion 8 k % % y is computed for nodes type ^ , j
Г 5 2 8 kw ) 8 k w i +1, j +1 - 8 k u i , j +1 + 8 k u i , j -1 - 8 k u i +1, j
_ .
I 5% 5y J . 2 X % X y
b, j
In node type i , n
Г 5 2 8 kw ) _ 8 k w i +1, j +1 -8 k u i -1, j +1 +8 k u i -1, j -8 k u i +1, j
I 5%5y I " 2XX .
v / i,n % y here, k _ 1, 2 .
Note the peculiarity of the application of the variational-difference approach. At the free edges of the plate during forming the matrices of stiffness and inertias of matrices to calculate the internal forces discrete equilibrium equations at internal nodes of the finite-difference mesh, and the nodes on the path were recorded.
The dimension of the formed matrices and stiffness matrices of inertia do not coincide. For more about the equation equal to zero the bending moments and generalized reactions on the contour reduced the dimension of the stiffness matrix to the dimension of the matrix of inertia. These additional procedures of adding the corresponding rows and columns between matrices were automated for meshes with different density.
y
X %
X %
X y
x
X y
j + 1
n
j n-l
j -1
i - 1 ^- 1 i ^ i + 1
Fig. 1. Finite-difference grid: solid lines show main lines of a grid; dashed lines show the supplementary grid
Numerical analysis. For the calculation of longitudinal-transverse bending of thin plates the mathematical package Maple [19] has been applied allowing calculations of the matrices eigenvalues and eigenvalues. Here there are two examples of calculating the stability from the forces of inertia.
Example 1 . Plate rigidly clamped along the contour; the volume force is equal X _ p a % _ 1 and Y _ p ay _ 0 . The dimensions in terms of l % _ 0,8 m; ly _ 0,6 m; h _ 0,01 m - the thickness. Of the Material of the plate has the features of stiffness: E _ 10 10 Па and p_ 0,45. Material density p _ 3000 kg/m3.
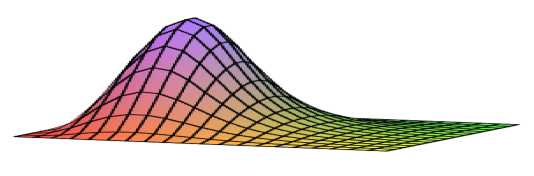
The first stage of the calculation involves the computation of the inner membrane of effort, the stress diagram of which is shown in fig. 2. Distribution of the basal surface is inhomogeneous. The warped view of the detected movements of the surface plates (fig. 3) can be seen in fig. 3. The solution of the generalized eigenvalues problem is the first form of transverse bending (fig. 3, b ).
The first eigenvalue is equal to 304 N/m3. The acceleration (N/m3)/ 3000(kg/m3) = 0.1 m/sec2.
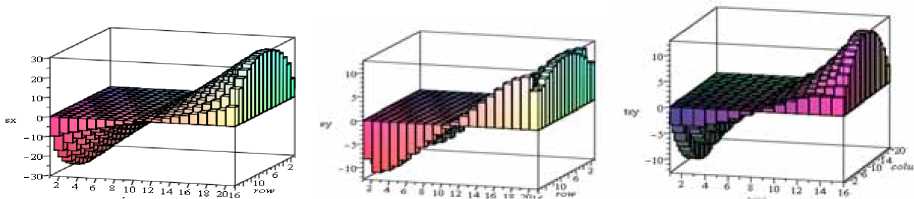
a b c
Fig. 2. Stress diagrams of the internal forces:
a – longitudinal Nx ; b – longitudinal Ny ; c – shift Sxy (the dimension of the internal forces N/m)
Example 2 . Let’s consider a plate fixed only at one end when the other three edges are free and not fixed. The plane is affected by constant acceleration. A similar calculation of longitudinal-transverse bending was presented in [2], where the effect of vertical cantilever plate of constant acceleration had been studied. To solve the problem the Ritz method is utilized.
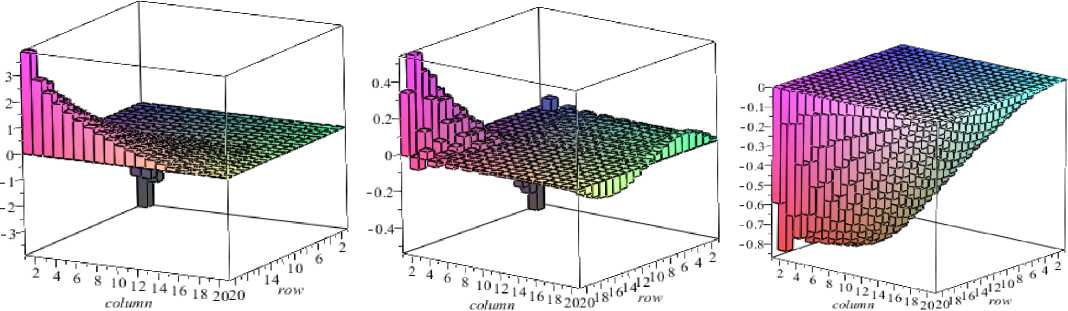
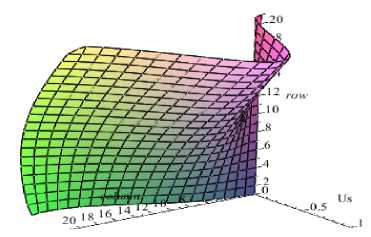
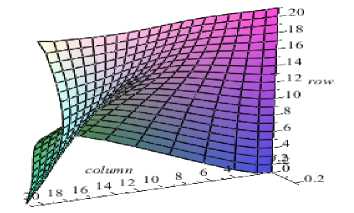
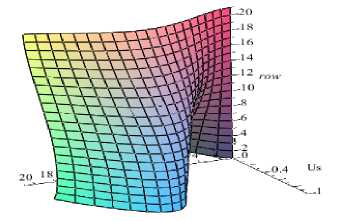
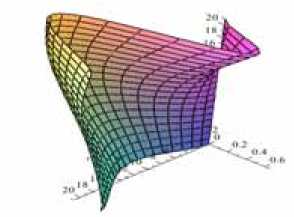
The plate has dimensions of 0,6×0,8 m, its thickness is 0,1·10–3m; Young’s Modulus of the material is equal to 2 •1011Pa; Poisson’s ratio is equal to 0,25; the density is 7800 kg/m3 (specific weight 76440 N/m3). The acceleration ay (for this option) is directed along the x-axis. It is necessary to determine the critical acceleration. Fig. 4 shows a deformed view obtained at the first stage the solution of the problem before the occurrence of critical acceleration. In fig. 5 we can see a view of the functions of internal heterogeneous membrane of efforts leading to the loss of stability. In fig. 6 we can see the resulting buckling of the plate; it also indicates the first four critical accelerations, corresponding to these forms. Note that Maple has chosen a negative value for the first and fourth eigenvalues corresponding form (fig. 6, a, d) in the opposite direction. At first glance, the negative value of the eigenvalues is contrary to the criterion of loss of stability, if the minimum eigenvalue is positive, then the design is stable. Here we considered a generalized problem [ A ]{w} = s* [B ]{w}, s* = 1/ s . If we always have [ A]> 0, then s* [B]> 0 should be greater than zero, not its own value s* .
b

a b
c
Fig. 5. Spatial view of stress diagrams for internal forces: а - N x ; b - N y ; c - S xy
b
d
Fig. 6. Forms of stability loss during acceleration: a – 2.9 m/s2; b – 3.0 m/s2; c – 4.0 m/s2; d – 4.3 m/s2
Conclusions. Thus, the approach to the calculation of plates can be used to calculate the critical values of the acceleration during acceleration or braking for the selection and analysis of geometric parameters and stiffness parameters of panels used in aerospace engineering. It is possible to identify a set of critical acceleration, which cannot be allowed in the operation of the thin panels.
The stiffness matrix and the matrix of the internal forces was formed by using an application program interpreter of Maple that have limited the thickening of the finite-difference grid for solving large-scale problems and consistently investigate the convergence of the results. Therefore, further research should apply for the program based on algorithmic languages of a higher level.
Needless to say, to search the entire spectrum of eigenvalues and forms the program Maple was spent by two orders of magnitude longer compared to the time of formation of the matrices. Thus, a subroutine for calculating eigenvalues using the method of scalar products has been developed for calculating the maximum eigenvalue. However, this requires the computation of the inverse stiffness matrix. Internal force matrices didn’t have inverse matrices.
Список литературы Calculating lateral deflection of plates subjected to heterogeneous forces of inertia using a variation-difference method
- Szilard R. Theories and Applications of Plate Analysis: Classical, Numerical and Engineering Methods. John Wiley & Sons, Inc., 2004. 1039 p.
- Xiang Y., Kitipornchai S., Wang C. Y. Buckling and spanning capacity of cantilevered vertical plates under body forces//The IES Journal. Part A: Civil & Structural Engineering. 2008. P. 116-122.
- Тимошенко С. П. Устойчивость упругих систем. М.; Л.: ОГИЗ-ГОСТЕХИЗДАТ, 1946. 532 с.
- Балабух Л. И., Алфутов Н. А., Усюкин В. И. Строительная механика ракет. М.: Высш. шк., 1984. 391 с.
- Строительная механика летательных аппаратов: учебник для авиационных специальностей вузов/И. Ф. Образцов . М.: Машиностроение, 1986. 536 с.
- Филоненко-Бородич М. М. Теория упругости. М.; Л.: ОГИЗ, 1947. 300 с.
- Тимошенко С. П., Гудьер Дж. Теория упругости. М.: Наука, 1975. 576 с.
- Сабиров Р. А. Особенности дифференциальной и вариационно-разностной формулировок задачи продольно-поперечного изгиба стержня от сил инерции//Вестник СибГАУ. 2014. № 3(55). С. 131-138.
- Яблонский А. А., Норейко С. С. Курс теории колебаний. М.: Высш. шк., 1966. 255 с.
- Васидзу К. Вариационные методы в теории упругости и пластичности: пер. с англ. М.: Мир, 1987. 542 с.
- Ван Цзи-де. Прикладная теория упругости. М.: Физматгиз, 1959. 400 с.
- Вольмир А. С. Устойчивость упругих систем. М.: Физматгиз, 1963. 880 с.
- Лейбензон Л. С. Курс теории упругости. М.; Л.: ОГИЗ, 1947. 465 с.
- Lopatin A. V., Morozov E. V. Approximate buckling analysis of the CCFF orthotropic plates subjected to in-plane bending//International Journal of Mechanical Sciences. 2014. № 85. P. 38-44.
- Ланцош К. Вариационные принципы механики: пер. с англ. М.: Мир, 1965. 408 с.
- Новожилов В. В. Основы нелинейной теории упругости. М.; Л.: ОГИЗ-ГОСТЕХИЗДАТ, 1948. 112 с.
- Михлин С. Г. Вариационные методы в математической физике. М.: Наука, 1970. 512 с.
- Самарский А. А. Теория разностных схем. М.: Наука, 1977. 656 с.
- Матросов А. В. Maple 6. Решение задач высшей математики и механики. СПб.: БХВ-Петербург, 2001, 528 с.


