Cамодействие скалярного заряда в заряженной экстремальной анти-дилатонной кротовой норе

Кротовые норы — это топологические ручки в пространстве-времени, связывающие различные вселенные или удаленные части одной и той же вселенной. Интерес к таким конфигурациям восходит к работе Флама [1], написаннной еще в 1916 году. Впоследствии, оживление интереса к этой теме связано с работой Эйнштейна и Розена [2] и более поздней серией работ Уилера [3]. Современный интерес к кротовым норам был порожден работами Морриса, Торна и Юртсеве-ра [4,5]. Хорошо известно, что в рамках классической общей теории относительности проходимые кротовые норы могут порождаться только экзотическим веществом, нарушающим нулевое энергетическое условие 〃" и^и" >  0, г де 〃“ — тензор энергии-импульса вещества, искривляющего пространство-время, а и* — произвольный световой вектор. Решения, описывающие кротовые поры, были получены в рамках различных моделей, таких как теории со скалярными полями [6, 7];

• ¹    E-mail: alsucuk@gmail.com

• ²    E-mail: apopov@kpfu.ru

теории Эйнштейна-Гаусса-Бонне [8, 9]; в рамках полуклассической теории гравитации [12-14]; в модифицированных теориях гравитации [15-19] и т.п. Описание геометрии кротовых нор, а также обзор по рассматриваемой теме могут быть найдены в книге Виссера [22].

Для удалённого наблюдателя статические сферически симметричные кротовые норы выглядят как черные дыры. Эффект самодействия заряда на себя является одним из эффектов, позволяющих различить эти два пространства-времени. Такой эффект для зарядов различных типов в искривленном пространстве-времени изучался в ряде работ. Обзор этих работ можно найти в [23-26]. Эффект самодействия заряда на себя связан с нелокальной структурой поля, источником которого является заряд, и определяется геометрией всего пространства-времени и его топологией. В плоском пространстве-времени этот эффект определяется третьими производными по времени от координат заряда. Сила самодействия для электрически заряженных частиц в плоском пространстве-времени дается формулой Абрахама-Лоренца-Дирака [27, 28].

В статическом искривленном пространстве-времени и пространстве-времени с нетривиальной топологией сила самодействия может отличаться от нуля даже для заряда, находящегося в состоянии покоя (здесь и дальше слова «в состоянии покоя» означают, что скорость заряда коллинеарна времениподобному вектору Киллинга, который всегда существует в статическом пространстве-времени). Такого типа результаты были получены для статических зарядов в плоских пространствах-временах с топологическими дефектами [29-35]. Формальное выражение для силы самодействия электрического заряда в произвольном искривленном пространстве-времени было впервые получено ДеВиттом и Бремом [36], а некоторые исправления были позднее сделаны Хоббсом [37]. Мино, Сасаки и Танака [38] и независимо от них Куинн и Вальд [39] получили аналогичное выражение для силы гравитационного самодействия точечной массы. Сила самодействия заряда, взаимодействующего с безмассовым минимально связанным с кривизной скалярным полем, источником которого является этот заряд, рассматривалась Куинном [40]. Недавний интерес к эффекту гравитационного самодействия был порожден попытками промоделировать излучение гравитационных волн двойными системами [41-43]. Этот интерес был вызван подготовкой детекторов гравитационных волн, излучаемых при падении компактного объекта на сверхмассивную черную дыру. Для черной дыры Шварцшильда сила самодействия статического заряда q была вычислена в работах [44,45] / 〜 q²/r³, г де г — шварцшильдова радиальная координата заряда.

Значительные усилия были предприняты для расчета силы самодействия на фоне различных типов черных дыр [46-68]. Сила самодействия для покоящегося заряда в пространстве-времени статической сферически симметричной кротовой норы определяется профилем горловины кротовой норы и константой связи скалярного поля с кривизной пространства-времени [69-77]. В работах [72,76] было показано, что существует бесконечный набор значений константы связи скалярного поля с кривизной, для которого сила самодействия на статический скалярный заряд расходится. Природа этого расхождения не совсем ясна. Целью настоящей статьи является анализ эффекта самодействия для статического скалярного заряда в экстремальной заряженной анти-дилатонной кротовой норе, описанной в [78,79]. Эта проблема имеет математические трудности. Поле заряда в рассматриваемой задаче определяется функцией Грина некоторого обыкновенного неоднородного дифференциального уравнения второго порядка (см. уравнение (7) ниже). Эта функция Грина может быть выражена в виде произведения независимых решений соответствующего однородного уравнения. Как правило, вронскианы таких решений совпадают, с точностью до константы нормировки, с коэффициентом перед дельта-функцией в уравнении на функцию Грина. В рассматриваемом случае это не так. Чтобы решить эту проблему, мы использовали свойства дельта-функции (см. ⑼)， что позволило свести задачу к стандартному случаю. Статья организована следующим образом. В разделе II мы описываем геометрию пространства-времени экстремальной заряженной анти-дилатонной кротовой норы и получаем неперенормированное выражение для потенциала самодействия статического скалярного заряда на рассматриваемом гравитационном фоне. В разделе III описывается процедура перенормировки потенциала самодействия и результат.

В статье мы используем единицы с = G = 1.

1.    Потенциал самодействия статического скалярного заряда

Метрика пространства-времени экстремальной заряженной анти-дилатонной кротовой норы может быть записана в следующем виде [78,79]

ds2 = -е-2”，)^2 + е2М，)[dr2 + (г2 + Q2)(d92 + sin2 %屮2)],                ⑴ где -а < r < 0。е [0,7т],д е [0, 2тт],

2a(r)

7Т²                  Г 、

丁^{- arctan} 丿,

⑵

a Q — электрический заряд кротовой поры, М — масса кротовой поры и Q 。一 дилатоішый заряд кротовой норы связаны следующими соотношениями

八         ТТ²…

⑶

^Qф = ^М = у l^Ql-

Рассмотрим скалярное поле 0, создаваемое источником j. Соответствующее уравнение поля имеет вид

嘅 =^-4?r^j

-4тгд / S ( ⁴⁾ (t “ ,3 “ (t ))         ,

⑷

где g ( ⁴⁾ — определитель метрического теігзора д^ 、 q — скалярный заряд 口丁一 его собственное время. Функции 5H( 丁 ) определяют мировую линию заряда. Для неподвижной частицы в статическом пространстве-времени (1) уравнение поля (4) можно переписать следующим образом

卜一 ² 。

' д²

▽ +

2rd     1    / д²     д

(r² + Q²) d + (r² + Q²) 〈福 ^{+cot Ө}дӨ

1    d² 、

+ sin² (Ө) dg² 丿

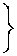
0(r, Ө, g; г,Ө, 冋 =-

47rqb ( r, r ) b ( 0, 0 ) b ( g, 冋 e³“(r² + Q²) sin Ө

⑸

где принято во внимание, что для статического заряда d 丁/必 = ，一 д^ = е^-"" ) . В силу сферической симметрии рассматриваемой задачи потенциал может быть представлен в виде

∞

0 = 4vrq £ 匕/О)匕幫(C)a(r,r) = q £ (2/ + 1) Pi (cos))g((r,r),              ⑹ l,m                               i=0

где Yi_m(O) — с ( 1 ) ерііческпе ( 1 ) уііктпш аргумента О = (Ө, g). cos 7 三 cos Ө cos Ө + sin Ө sin Ө cos(g - 冋 . Радиальная часть потенциала gi, удовлетворяет уравнению

d2 gi(r,r) + dr2	2r     dgi(r,r)     /(/ +1) (r2 + Q2)   dr      (r2 + Q2)gi(r ， r)=	b(r, r)	⑺
		e@ (，) (r2 + Q2).
Вводя новую функцию	Gi (r, r) = ea(r)gi (r, r)		⑻

и учитывая

8(r,r) 8(r,r) е@(,)      еМ，) , можно получить следующее уравнение для Gi (r, r)

d2Gi(r,r)        2r dGi(r, r)     /(/ +1)                   b(r,r)

—豆— ⁺ (r² + Q²) —dr     (r² + Q²) ¹ss = - (r² + Q²).

Обозначим два независимых решения соответствующего однородного уравнения d2 田 +   2r   dW - - +1)平=0

dr2    (r2 + Q2) dr    (r2 + Q2)

⑼

Wi(r) и W?(r) . Wi(r) выберем так, чтобы при r т +^ это решение стремилось к нулю, а при r т —а расход ил ось. W?(r) выберем так, чтобы при r т +^ это решение расходилось, а при r т —а стремилось к нулю, т.е.

lim W

■ Т + 8

lim W

■ Т — 8

0, lim W2 = а, ■ Т + 8

а, lim Ф2 = 0.

■ Т — 8

Тогда решение уравнения (10) можно представить в следующем виде

Gl = Ө(r - 亍 )w1 ( e)w2 ( 亍 )+ 9( 『 -r)w1 ( 6)w2 ( ? ) .

Нормировка W достигается путем интегрирования (10) по r от (r — е) до (r + е) и взятия предела е т 0. Это приводит к условию на вронскиан

,       、        dW2       dWi        1

爪 ^(W1 , ^W2) = ^W1 而 - ^W2 而 = 戸—.

Рассмотрим уравнение (11) в областях r > 0 и r < 0. Мы можем построить независимые решения этого уравнения для этих двух областей

0+(r)

Pi

0-(r)

Pi

/ 1r 、

(南丿,

G -ir\

Q 丿^,

。 +(r) = Qi

。 -(r) = Qi

/ ir 、

(目丿,

G -ir 、

Q 丿^,

r > 0,

r < 0,

где Pi and Qi многочлены Лежандра первого ВИД

и второго рода. Асимптотики этих решений имеют

.

Вронскиан 0±, 0± легко вычисляется (см. [80])

%(。 ± ，。 ± )=黒. / ⁺ Q

Решения (11) во всём пространстве можно записать следующим образом

Wi

W2

[叶 0 + + / + 。 +	r > 0,
{ а—0— +/—0—	r < 0,
[ a + 0 + + 户 + 0 +	r > 0,
{ а—0— + /—0—	r < 0,

где а±² ,/3±² являются константами. Подставляя граничные условия (12) в (18) и используя (16) получим

旺 =^0,

а— = 0.

Тогда выражения (18) сводятся к следующему виду

W1		/+0+ aL0 — + 死 02	r > 0, r < 0,
W2	{	a+0+ + /+0+ /—02	r > 0, r < 0.

Подставляя эти выражения в вронскиан и принимая во внимание (17), получим

爪 (Wl , W2)

ад

(r2 + Q2), i|Q|

r > 0,

r < 0.

Сравнивая это выражение с (14), получим следующие соотношения между коэффициентами:

»+/+ = Q—/—

—17

~：---Г = г.

7IQIIQI

Выпишем условия сшивки решений Ф1 (r) и W?(r)

при r = 0

lim Фі(г) = lim Фі(г),

■т+о        ■т —о

lim

■т+о

lim w2 什) =lim w2 什),

■т+о        ■т —о

lim

■т+о

d%(r) dr d^2(r) dr

lim

■т —о

lim

■т —о

d%(r)

dr ， dW2(r)

dr

.

Используя эти условия и выражения (20), можно

получить следующие соотношения

/+Ф+ (0) = q — Ф—(0) + /—Ф—(0),

。 + 。 +(0) + / + ф + (0) = /—Ф—(0),

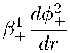
₁ d 。 — Q—— ； —

о

dr

о

i d 。 ^{2 +/1} 夫,

о

吸

d ( ^+

dr

Эти выражения можно разрешить относительно

Q—, /— , Q ：

+ о 4 ， /

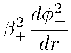
о

d 。 — dr

о

.

Q—= /+ …

Принимая во внимание (15)

4(0)

Qi (0)

,/1 = /+ о

%(0-,0+)

%(0-,0-)0,

▽ (0+,0-)

爪 (Ф*/)

爪 （Ф+ ， Ф+ ） о,

爪 (Ф+ ， Ф+ ) о .

и используя свойства функций Pi (z) и Qi (z) (см.Ref. [80]), получим

г( 2 -1)г(1 + 2)

,К(0)

^г( 2 +1^)г(-1) ，

—2 2 ( i+i ) ^г( 2 + 2)

Это позволяет вычислить вронскианы

г(1 + 2) ， в (26)

c "n 、   行—多 i^{г(1 +} )

Qi (0) = Е 2 йй!)

爪 (Ф+ ， Ф-)|о

N-1)i

IQI ，

爪 (Ф-,Ф+)|о

7 ： Н

Е^(-1) ,  爪 (О—^,Ф—)|о

|Q|

IQI ，

爪(ф+,ф+)|о = IQI ,爪(ф+，Ф—)|о = ■ и переписать выражения (26) следующим образом

7(-1)ⁱ IQI

Q1 = — 7 开 ( 一 1)' / + ， q + = 7 开 ( 一 1) /—,

Используя эти соотношения и выражения (13, 15, 20, 22), получим для r > r > 0

Gi (r, Г)

向

7 叩 (Ф+ ， Ф—) |Q| 口 (Ф+ ， Ф—)

Ф + (г)Ф + (г), о

7                                1

^ф + ^{( г ) ф} + ^{( г )} +       ^ф + ^{( г ) ф} + ^{( г )}

l^Ql                      万 l^Ql

， -—-    1 .

|Q| Qi(z)Pi(z) + ^|Q |Qi (z)Qi(z),

-        2質 〜     2質 где z = IQI …可 r > r > 0- Ө =。口夕=

Подставив это выражение в (8), а затем в (6), можно получить (для случая

冋

Ф(г, r)

q

£ ^—a ⑺

IQI

∞

£(2/ + 1)

і =о

7Н (Z)Qi (z) + ^Qi (Z)Qi (z) 穴

卜

Для вычисления первого члена рассматриваемой суммы можно воспользоваться формулой Гейне

(Heine) [80]

∞

£ (2/ +1)n( ； ?)Q ， (z)

(=0

г 一 г

При вычислении второго члена суммы воспользуемся интегральным представлением функции Ле жандра второго рода [80]

Q ( (z)

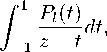
что позволяет получить следующее выражение

∞

e(2 ， +1)Q ((球) Q( (话

(=0

arctan 力 一 arctan т

/ 一 т

〜

Поэтому для г> 亍 > 0, Ө = 9ид = 0 получим

0(г, г)  = qe^-a(r^

r 一 Г

arctan

г

一 arctan

_7r (г 一 г)

г

2.    Перенормировка и результат

Процедура определения силы самодействия требует перенормировки скалярного потенциала 0(т; т), который расходится в пределе т т т (см., например, работы [81,82]). Такая перенормировка может быть достигнута путём вычитания коитрчлеиа деВитта-Швиигера %s (т; т) из 0(т; т) и взатия предела т т т

Фгеп(т) = lim (0(т; т) ― 0Ds (т; т)) .(36)

ŽT4

Коіітрчлен ДеВитта-Швиигера 。口 _s(т ; т ) для покоящегося скалярного заряда в статическом искривленном пространстве-времени имеет следующий вид [83]

ф0式心刃=q (£ + 册? 4gt；〜靑), где [84,85]

7 = 一 ( т^г 一 т^г ) 一 ； Г ； % (/ — т ) )( т* 一 т* )

— 6 (^ Г}_тГ^ +         (〃 一 #)( т* 一 т* )( т⁽ 一 т⁽ ) + О ( (т 一 т)⁴ ) ,

。=噌"丸

Г；* — символы Кристоффеля втор ого рода, вычисленные в точке т. Коитрчлеи ДеВитта-Швиигера 0ds(т; т) в переделе Ө = Ө, 0 = 0 легко вычисляется в пространстве-времени ⑴ qe-Mr)

фг>S (г, г)=-———.(39)

| г 一 г |

Используя выражение (35) для ф(г, г) получим переиормированное выражение для ф в области г > 0

фгеп(г) = lim [ф(г, г) — фоs (г, г)]= 一 蛆|：     .(4

r_r                         7(г2 + 包 2)

В области г < 0, фгеп совпадает с этим выражением из-за симметрии г 一 一г задачи. Асимптотика потенциала фгеп (г) пр и г т ^ имеет следующий вид фгеп(г) ~ 一处У .(41)

7rг2

Единственной ненулевой компонентой силы самодействия является

F『(г)

<7 ,, дфгеп(г)

2 g

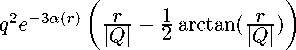
7tQ ² (1 + r²/Q²)²

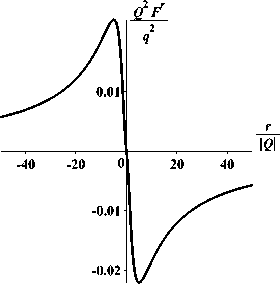
Таким образом, вычислено аналитическое выражение (55) для силы самодействия статического скалярного заряда в пространстве-времени экстремальной заряженной кротовой норы (1).

Работа выполнена за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров.