Cascaded Factor Analysis and Wavelet Transform Method for Tumor Classification Using Gene Expression Data

Published Online August 2012 in MECS

Microarray has emerged as advanced biological laboratory technology accrued a huge amount of gene expression profiles of tissue samples at relatively low cost and facilitates the scientists and researchers to characterize complex biological problems. Microarray technology has been used as a basis to unravel the interrelationships among genes such as clustering of genes, temporal pattern of expressions, understanding the mechanism of disease at molecular level and defining of drug targets [1]. Among the above types diseases classification and analysis has gained a special interest. Especially tumor classification through the gene expression profiles has center of attraction in many research communities as it is important for subsequent diagnosis and treatment. Gene’s expressions are stained at different conditions or different cellular stages to reveal the functions of genes as well as their regulatory interactions. Gene expression of disease tissues may be use to gain a better understanding of many diseases, such as different types of cancers.

Empirical microarray data produce large datasets having expression levels of thousands of genes with a very few numbers (upto hundreds) of samples which leads to a problem of “curse of dimensionality”. Due to this high dimension the accuracy of the classifier decreases as it attains the risk of overfitting. As the microarray data contains thousands of genes, hence a large number of genes are not informative for classification because they are either irrelevant or redundant. Hence to derive a subset of informative or discriminative genes from the entire gene set is necessary and a challenging task in microarray data analysis. The purpose of gene selection or dimension reduction is to simplify the classifier by retaining small set of relevant genes and to improve the accuracy of the classifier. For this purpose, researchers have applied a number of test statistics or discriminant criteria to find genes that are differentially expressed between the investigated classes.

Various methods and techniques have been developed in recent past to perform the gene selection to reduce the dimensionality problem. The filter method basically use a criterion relating to factors and select key genes for classification such as Pearson correlation coefficient method [1], t-statistics method [2], signal-to-noise ratio method [3], the partial least square method, independent component analysis [4], linear discriminant analysis and principal component analysis [5].All the methods transform the original gene space to another domain providing reduced uncorrelated discriminant components. These methods do not detect the localized features of microarray data. Hence Liu [6, 7] proposed a wavelet basis function to perform the multi resolution analysis of the microarray data at different levels. The relevant genes of the microarray data can be measured by wavelet basis based on compactness and finite energy characteristic of the wavelet function. It does not depend on the training samples for the dimension reduction of the microarray data set. It also does not require a large matrix computation like the LDA, PCA and ICA, so simpler to implement. Due to these characteristics of wavelet, in this paper we have used the wavelet based feature extraction to reduce the feature space. Still some redundant genes are also present in the reduced gene set which may mislead the accuracy. Thus in this paper we introduced a promising ranking method known as F-score statistics to use in conjunction with the wavelet transform to get the optimal relevant and discriminative genes for classification.

Several Machine learning and statistical techniques have been applied to classify the microarray data. Tan and Gilbert [8] used the three supervised learning methods such as C4.5 decision tree, bagged and boosted decision tree to predict the class label of the microarray data. Dettling [9] have proposed an ensemble method of bag boosting approach for the same purpose. Many authors have used successfully the support vector machine (SVM) for the classification of microarray data [10]. Khan et al. [11] used the neural networks to classify the subcategories of small round blue-cell tumors. Also O’Neill and song [12] used the neural networks to analyze the lymphoma data and showed very good accuracy. B Liu et al. [13] proposed an ensemble neural network with combination of different feature selection methods to classify the microarray data efficiently. But the conventional neural networks require a lot of computation and consume more time to train. In this paper we have introduced a new promising low complexity neural network known as radial basis function neural network (RBFNN) to efficiently classify the microarray data.

The remainder of this paper is organized as follows: Section 2 presents the details of the dataset used for the study in the paper. Section 3 presents the proposed methods for tumor classification using gene expression data and Section 4 presents the Simulation of the experiment and result analysis of the proposed methods. Section 5 draws the conclusions of this paper.

• II.    Dataset

• 2.1    ALL/AML Leukemia Dataset

  The dataset consists of two distinctive acute leukemias, namely AML and ALL bone marrow samples with 7129 probes from 6817 human genes. The training dataset consists of 38 samples (27 ALL and 11 AML) and the test dataset consists of 34 samples (20 ALL and 14 AML).

• 2.2    SRBCT Dataset

  The dataset consists of four categories of small round blue cell tumors (SRBCT) with 83 samples from 2308 genes. The tumors are Burkitt lymphoma (BL), the Ewing family of tumors (EWS), neuroblastoma (NB) and rhabdomyosarcoma (RMS). There are 63 samples for training and 20 samples for testing. The training set consists of 8, 23, 12 and 20 samples of BL, EWS, NB and RMS respectively. The testing set consists of 3, 6, 6 and 5 samples of BL, EWS, NB and RMS respectively.

• 2.3    MLL Leukemia Dataset

  The dataset consists of three types of leukemias namely ALL, MLL and AML with 72 samples from 12582 genes. The training dataset consists of 57 samples (20 ALL, 17 MLL and 20 AML) and the test data set consists of 15 samples (4 ALL, 3 MLL and 8 AML).

• 2.4    Colon Dataset

  The dataset consists of 62 samples from 2000 genes. The training dataset consists of 42 samples where (30 class1, 12 class2) and the test data set consists of 20 samples (10 class1, 10 class2).

In this section, the cancer gene expression data sets used for the study are described. These datasets are also summarized below.

• III.    Proposed Methods3.1    Factor analysis

It is a statistical method used to describe variability among observed, correlated variables in terms of a potentially lower number of unobserved variables called factors. It is possible, that variations in three or four observed variables mainly reflect the variations in fewer such unobserved variables. Factor analysis searches for such joint variations in response to unobserved latent variables. The observed variables are modeled as linear combinations of the potential factors, plus "error" terms.

The information gained about the interdependencies between observed variables can be used later to reduce the set of variables in a dataset.

Given a set of variables, the underlying dimensions account for the patterns of co-linearity among the variables. It is a data reduction tool that removes redundancy or duplication from a set of correlated variables and retains some smaller set of derived variables.

There are two types of variables, such as factors and observed variables. Select and measure a set of variables, Extract the principal factors analyzes covariance (but not unique variance and error variance) produces "factors", a linear combination of all factors, approximates, but does not duplicate, the observed correlation matrix. Its purpose is to reproduce the correlation matrix (with a few orthogonal factors).Factors is formed that are relatively independent of one another.

Determine the number of factors to retain

• 1)    Eigen values: retain all factors with EV > 1

• 2)    Scree plot: retain all factors "before the elbow"

When more than one factor is retained, unrotated factors cannot be interpreted in most cases. Rotation does not affect the mathematical fit of the solution.

Orthogonal rotation: The factors are uncorrelated (= orthogonal).

Oblique rotation: The factors may (or may not) be correlated.

If rotation is orthogonal, the data are interpreted from the "loading matrix" (SPSS: "rotated factor matrix"). The values in this matrix are bivariate correlations between the variables and the factors. If rotation is oblique, the data are interpreted from the "pattern matrix". The values in this matrix are partial correlations between the variables and the factors. In both cases, the values are called "factor loadings". If rotation is oblique, the "structure matrix" contains the bivariate correlations between variables and factors (to be ignored).

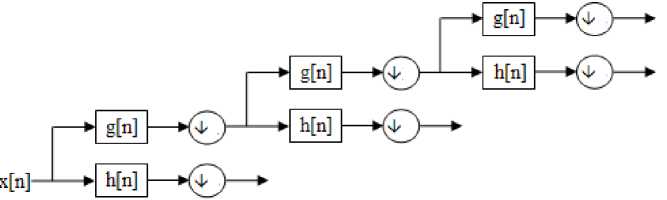
Fig.1: Wavelet decomposition

The wavelets can be realized by iteration of filters with rescaling which was developed by Mallat [15] through wavelet filter banks. The resolution of the signal, which is a measure of the amount of detail information in the signal, is determined by the filtering

We now postulate that there are q factor variables, and each observation is a linear combination of factor scores F ir plus noise:

Χ =ϵ +∑ F W (1)

The weights w rj are called the factor loadings of the observable features; how much feature j changes, on average, in response to a one-unit change in factor score r. Notice that we are allowing each feature to go along with more than one factor (for a given j, w_r j can be nonzero for multiple r). This would correspond to our measurements running together what are really distinct variables.

• 3.2    Wavelet based feature extraction method

Wavelet transform proposed by Grossman and

Morlet   [14]   is an efficient time-frequency representation method which transforms a signal in time domain to a time-frequency domain. The basic idea is that any signal can be decomposed into a series of dilations and compressions of a mother wavelet

V ^(t)

.

Hence the continuous wavelet transform of a signal is defined as:

CWT ( a , b ) = -1= Г x ( t ) ^ ( t—b d    ⁽²⁾

V a -”     к a )

where ^_a (tt ) =     V f t—b ), a e R ⁺ , b e R

^,       V a  к a )

The resolution of the signal depends on the scaling parameter ‘ a ’ and the translation parameter ‘ b ’ determines the localization of the wavelet in time. The CWT can be realized in discrete form through the discrete wavelet transform (DWT).The DWT is capable of extracting the local features by separating the components of the signal in both time and scale. In the microarray data the gene expression profile is considered as a signal which can be represented as a sum of wavelets at different time shifts and scales using the DWT as shown in figure 1.

operations, and the scale is determined by up sampling and down sampling operations. The approximation coefficients obtained by the decomposition at a particular level is used as the features for further study.

• 3.3    Radial basis function neural network classifier

For function approximation and pattern classification problems we are using the radial basis function neural network (RBFNN) which is a neural structure because of their simple topological structure and their ability to learn in an explicit manner. In the classical RBF network, there is an input layer, a hidden layer consisting of nonlinear node function, an output layer and a set of weights to connect the hidden layer and output layer. Due to its simple structure it reduces the computational task as compared to conventional multi layer perception (MLP) network. In RBFNN, the basis functions are usually chosen as Gaussian and the number of hidden units are fixed apriori using some properties of input data. The structure of a RBF network is shown in Fig. 2.

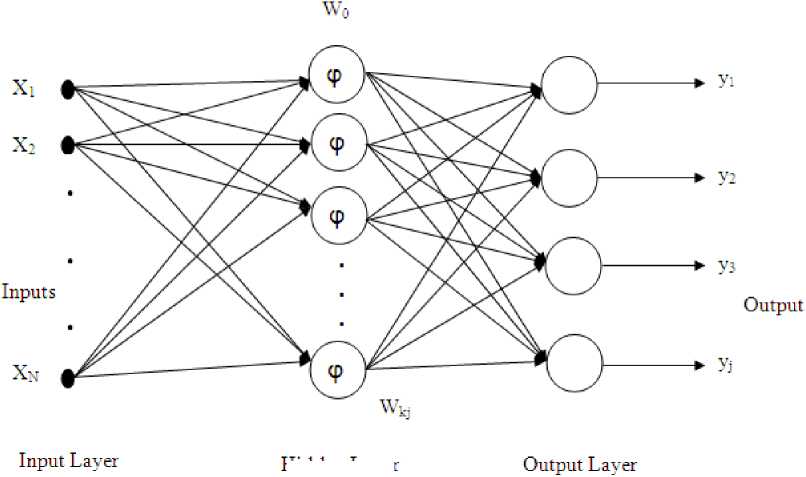
Hidden Layer

Fig. 2: The RBFNN based classifier

For an input feature vector x, the output of the jth output node is given as.

NN -II x(n) - C_k 1

y j = ∑ w kj ϕ k = ∑ w kj e    ^{2 σ k}     (3)

k = 1              k = 1

The error occurs in the learning process is reduced by updating the three parameters, the positions of centers (C k ), the width of the Gaussian function (σ k ) and the connecting weights (w) of RBFNN by a stochastic gradient approach as defined below:

w(n + 1) = w(n) -µ _w   J(n)

∂w

C k (n + 1) = C k (n) -µ c ^∂ J(n)

∂Ck

∂

σ _k(n + 1) =σ _k(n) -µ_σ

∂σk where J(n) = e(n) , e (n) =d (n) - y (n) is the error, d (k) is the target output and y (k) is the predicted output. µ µ And µ are the learning parameters of the RBF network. The complete process of the proposed feature extraction based classification process is presented in Fig. 2.

• IV.    Experiment and Analysis

In order to compare the efficiency of the proposed method in predicting the class of the cancer microarray data we have used three standard datasets such as Leukemia, SRBCT and MLL Leukemia. All the datasets categorized into two groups: binary class and multi class to assess the performance of the proposed method. The Leukemia dataset is binary class and both SRBCT and MLL Leukemia are Multi class datasets. The feature selection process proposed in this paper has two steps. First the microarray data is decomposed by factor analysis optimally choose the discriminate feature set then using Discrete wavelet transform into level 4 using db7 wavelet to get the approximation coefficients as the extracted feature set. The performance of the proposed feature extraction method is analyzed with the well studied neural network classifiers such as MLP and RBFNN. The leave one out cross validation (LOOCV) test is conducted by combining all the training and test samples for both the classifiers with all the three datasets and the results are listed in Table 1. For binary class the performance of RBFNN is comparable to MLP, but in case of multi class it outperforms the MLP.

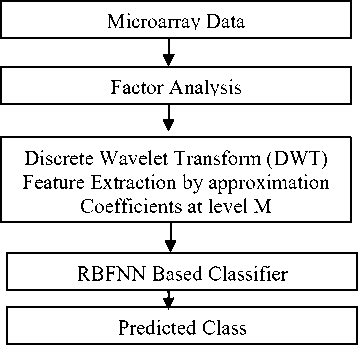
Fig.3: Flow graph of the proposed feature extraction based classification method

Table 3 Comparison study of accuracy of SRBCT dataset

Methods	Classification accuracy
SLDA	100 %
BWNN	96.83 %
C4.5	91.18%
Bagboost	95.24 %
SVM	93.65 %
TPCR	100 %
Gradient LDA	100 %
Factor Analysis + Wavelet + RBFNN	97.59 %

Table 1 Comparison study of classification accuracy of MLP and RBFNN classifiers

Dataset	Method	Classification Accuracy
Leukemia	MLP	98.61 %
	RBFNN	100 %
SRBCT	MLP	90.36%
	RBFNN	98.59%
MLL Leukemia	MLP	87.50%
	RBFNN	98.83%
Colon	MLP	93.54%
	RBFNN	96.33%

Table 2 Comparison study of accuracy of Leukemia dataset

Methods	Classification accuracy
Bayesian Variable	97.1 %
PCA disjoint models	82.3 %
Between-group analysis	88.2 %
C4.5	91.18%
Bagging C4.5	91.18 %
Adaboost C4.5	91.18 %
SFFS+PCA+SVM	58.82 %
SFFS+ICA+SVM	91.18 %
Combined feature selection + ensemble neural network	100 %
Wavelet + GA	100 %
Factor Analysis + Wavelet + RBFNN	100%

Table 4 Comparison study of accuracy of MLL Leukemia dataset

Methods	Classification accuracy
C4.5	73 %
Bagging C4.5	86.67 %
Adaboost C4.5	91.18 %
Wavelet +GA	100 %
Li’s rule based method	100 %
Combined feature selection + ensemble neural network	100 %
Factor Analysis + Wavelet + RBFNN	96.87%

The performance of the proposed method is also compared with those obtained by the recently reported methods and the results are listed in Table 2-4. The existing methods also used the cross validation test on the datasets. From Tables 2-4 it reveals that our method is equivalent to the counterparts with the advantage of reduced computational load. Table 5 shows the decomposition stages upto 4th level by using db7 in discrete wavelet transform.

Table 5 Reduction details of the dataset

Dataset	Original Dimension	Factor Analysis	DWT (Dubecies7) Level 4
Colon	62х 2000	62х 700	62х 184
SRBCT	83х 2308	83х 700	83х 184
Leukemia	72 х 7129	72х 700	72х 184
MLL Leukemia	72х 12582	72х 700	72х 184

• V.    Conclusion

In this paper we have presented a hybrid feature extraction method using the Factor analysis in

Cascaded Factor Analysis and Wavelet Transform Method for

Tumor Classification Using Gene Expression Data conjunction with wavelet transform to effectively select the discriminative genes on microarray data. A simple RBFNN based classifier has also been introduced to classify the microarray samples efficiently. The comparison results elucidated that the proposed approach is an efficient method which performs better than the existing methods. Besides it has reduced computational complexity.