Целевая функция из критериев оптимизации с весовыми коэффициентами

В качестве примера применения целевой функции рассмотрена оптимизация малошумного многоступенчатого герметичного насоса с тремя критериями оптимизации: отклонение от заданных значений напора, кавитационные качества и пульсации давления, вызывающие гидродинамический шум.

Наряду с вышеуказанными критериями оптимизации в данном случае использовался критерий, характеризующий интенсивность пульсаций давления на входе в направляющий аппарат (Рисунок 1):

/ Ai \

Р‘=2(М^Ы где A – амплитуда пульсаций давления заданной частоты на входе в направляющий аппарат.

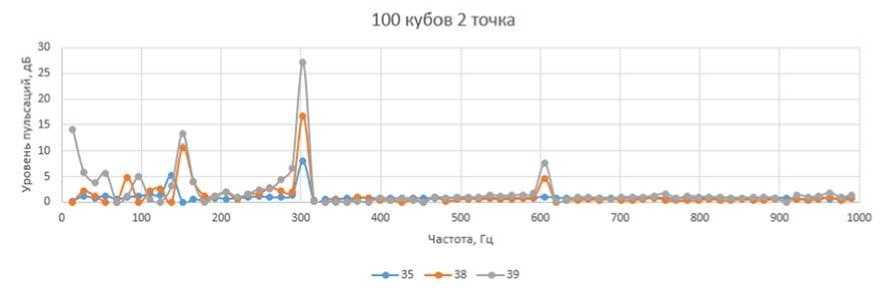
Рисунок 1. Разложение в спектр сигнала пульсаций давления

В результате расчета 32 моделей по ЛП-тау алгоритму оптимизации получается следующая таблица результатов (все критерии приведены к безразмерному виду) (Таблица 1).

Таблиц а 1. Результаты оптимизации насоса по четырем критериям

№ модели	K 1H ,%	K 2H , %	С кав , %	P, %
0	4,46	309	4,14	12,1
1	4,65	114	22,1	14,8
…
31	16,5	15,8	21,5	6,37

При небольшом количестве рассчитанных моделей есть возможность выбрать наилучший вариант, проанализировав таблицу результатов.

Другим вариантом является введение целевой функции с весовыми коэффициентами для каждого критерия:

L=L H K 1H +L H K 2H +L кав C кав +L P P

Для различных значений коэффициентов в зависимости от конкретных требований к насосу можно выбрать различные проточные части (Таблица 2).

Таблица 2. Выбор различных проточный частей в зависимости от значений весовых коэффициентов

Значение весовых коэффициентов			Номер модели с мин. ЦФ	Значение ЦФ	Значение критериев оптимизации
L	L кав	L		L	K	K	C кав	P
1	0,1	0,1	22	15,0	1,86	11,52	2,21	14,1
0.1	1	0.1	22	4,96	1,86	11,52	2,21	14,1
0.1	0.1	1	31	11,7	16,55	15,826	21,40	6,34

Выбор критериев оптимизации также определяет используемую математическую модель в процессе расчета проточных частей. Во многих случаях нет необходимости использовать требующую существенных вычислительных ресурсов нестационарную модель.

Таблиц а 3. Выбор используемой математической модели в зависимости от выбранных критериев оптимизации

Стационарный расчет	Нестационарный расчет
Гидравлический КПД вблизи оптимума	Виброакустические свойства
Статические нагрузки в оптимальном режиме	Нестационарные нагрузки
Напор вблизи оптимума	Напор, КПД, нагрузки в режимах

Критерий кавитации

вдали от оптимального

После выбора критериев оптимизации необходимо определиться с параметрами. Как уже говорилось, сложность состоит в том, что проточная часть насоса имеет очень много варьируемых геометрических параметров, и в процедуру оптимизации необходимо вовлекать только те из них, которые оказывают наибольшее влияние на выбранные критерии.

Возможно использование двух способов выбора параметров оптимизации:

• 1.    экспертная оценка на основе опыта проектирования и расчета первоначальной проточной части;

• 2.    оценка влияния параметров на критерии оптимизации расчетным путем.

Каждый из этих методов имеет свои преимущества и недостатки.

При постановке задачи оптимизации лучше всего комбинировать два этих подхода. При использовании второго подхода необходимо рассчитать некоторое количество проточных частей, изменяя только один параметр и так для каждого потенциального параметра оптимизации.

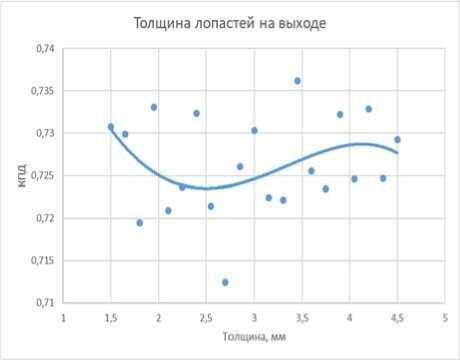
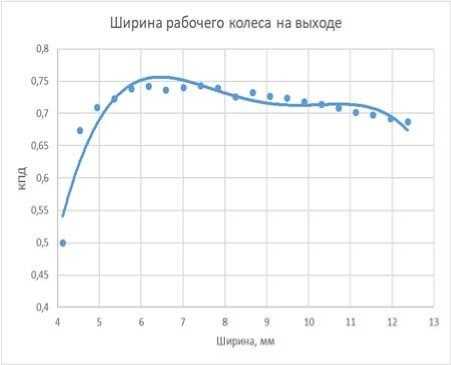
Ниже приведены два графика полученные для насоса низкой быстроходности иллюстрирующие такой подход (Рисунок 2).

Видно, что влияние ширины колеса гораздо существенней, поэтому она выбрана в качестве одного из критериев оптимизации.

Существенную сложность в процессе оптимизации проточной части методом численного моделирования представляет создание 3D-моделей проточной части.

При отсутствии программных кодов для построения элементов проточной части (как в случае отводящего устройства с разделительным ребром) возникает необходимость создания собственных средств для получения исходных для моделирования моделей.

а                                     б

Рисунок 2. Влияние толщины лопасти на выходе из рабочего колеса (а) и ширины на выходе из канала рабочего колеса (б) на гидравлический КПД