Chaotic Genetic Algorithm based on Lorenz Chaotic System for Optimization Problems

Published Online April 2013 in MECS

• I.    Introduction1.1    Review

N owadays, nonlinear optimization problems are one of the most important problems in computational theory. Because many of applications in the real world need to be optimize. There are many techniques to solve optimization problems and they also have been tried to improve their important measures such as time complexity. On the other hand there are many evaluation functions and benchmarks to evaluate optimization techniques and researchers are using them to evaluate their techniques and methods, the most famous of these functions are Schaffer, Clonalg, Bohachevsky, Rosenbrock, TSP (Travelling Salesman Problem), etc. Hyper-heuristic techniques and Evolutionary algorithms are two solutions for nonlinear optimization problems. The Genetic Algorithm is an evolutionary algorithm that can solve these problems. Evolutionary algorithms have many benefits in solving problems but they have a few disadvantages, one of the disadvantages is 'premature convergence' that is for

Random reason. Some evolutionary algorithms are GA, PSO, SA, ACO, etc. Many researchers introduced new improved methods based on the above techniques; Tsoulos [1] introduced a heuristic modified method based on the Genetic Algorithm. In that paper he modified genetic operators that preserve the feasibility of the trial solution encoded in the chromosomes. Also, there are hybrid algorithms to solve optimization problems; most of them trying to improve other important parameters such as time complexity, adaptability, stability, etc. Wei Juan [2] and his coauthor optimized the Fuzzy Rule Base with combination of the Genetic Algorithm and Ant Colony; their results show that the hybrid method can be more useful than the basic Genetic Algorithm. In another study, Sun Feng-jie [3] and his coauthor proposed an efficient hybrid method for image classification with PSO and GA; they used features of fast convergence of particle swarm optimization and diversity of genetic algorithm to improve their method.

• 1.2    Motivation for Using Chaotic Systems

Evaluation of Genetic Algorithms in optimization problems in previous studies have shown that premature convergence is a disadvantage to solve these problems; this is for randomness reason that use in Initial Population, Crossover and Mutation processes. Our experience says, deterministic pseudo-random data can be useful for diversity of Chromosomes and finally in the results. In fact pseudo-randomness and deterministic are two features of chaotic systems that are interesting in this paper. Since our research was shown that the Lorenz chaotic systems outperforms these other systems, we use it in the present research.

• 1.3    The-State-of-the-Art

Recently, use of the Chaos Theory and chaotic values has increased significantly, many of applications in different fields of nonlinear science and also computer science have employed Chaos Theory and achieved its benefits, such as Encryption algorithms that use a chaotic map to create secure images in image encryption techniques [4, 5, 6 and 7], using chaotic systems in Time Series Predictions [8 and 9] and Communication systems [10], for Clustering that Chang and Huang [11] proposed a chaos clustering approach based on Genetic Algorithm in their contribution and achieved both enhance to diversity and extract clustering rules for achieving a potential moving track of evolution to improve the convergence performance. Also in Optimization Problems [12 and 13] where Gandomi and his coauthors in [12] proposed a Chaotic Accelerated PSO that can outperform standard APSO with appropriate performance in comparison with other algorithms and in application to a complex problem. Most of the optimization methods which use chaotic systems instead of random processes trying to generate deterministic data with random values. The Genetic Algorithm, Particle Swarm Optimization and other Evolutionary Algorithms are some of the methods recently use chaotic systems.

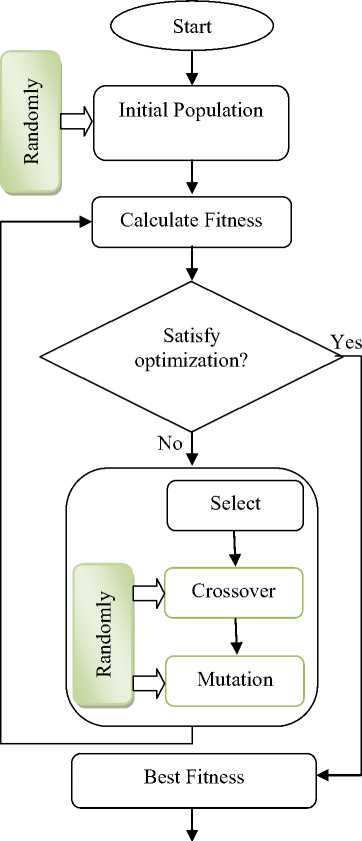
Fig. 1: Basic Genetic Algorithm flowchart

• II.    Basic Genetic Algorithm

  The Genetic Algorithm was introduced by Professor John Holland in the 1970s who took advantage of some phenomenon in natural evolution; he introduced his idea based on Darwin’s Biological Evaluation as an optimization algorithm. The main idea in this technique is derived from natural evolution so there are some biological operators such as Crossover, Mutation and Selection [14]. There are three part of this process which are randomly generated, namely the Initial Population, the Crossover and the Mutation. In the first step of the process, the Initial Population in the Genetic Algorithm generates some random solutions. In the second step, the random value of Crossover aid to make new offspring and in the third step, with random value of Mutation let to change a few of gens [15]. Figure 1 shows a flowchart of the basic Genetic Algorithm idea. Where there are some important sections such as Initial Population, Fitness evaluation, Crossover and Mutation. In general, the Genetic Algorithm strictly depends on Crossover and Mutation operators; this means that the Random function is very important in the Genetic Algorithm. The Genetic Algorithm has desirable time complexity, but it can still be improved further.

• III.    Chaotic Systems

The idea of using chaotic systems instead of a random process has been noticed in optimization problems. Chaos is a common non-linear phenomenon in nature, which fully reflects the complexity of the system. Chaos is random and has a clutter performance like a random variable [16]; in fact the rule of randomness can be played by chaotic dynamics instead of a random process [17]. Chaotic systems include features that can be important in optimization problems, such as:

• •    The sensitive dependence on initial conditions;

• •    The quasi-stochastic property;

• •    Ergodicity.

• 3.1    Lorenz Chaotic Systems

Implementation and Analysis of optimization based on chaotic systems in this paper show that the above features are important and they can improve the efficiency of the Genetic Algorithm in solving computational problems.

x = 10( y - x )

y = 28 x - xz + y                       (1)

z = xy — J z

The Lorenz system is one of the famous chaotic systems that it was introduced by Edward Lorenz. Lorenz system equations were introduced in equation

(1); the Lorenz system is a 3 dimensional system and its lyapunov exponents have been shown in figure 2, where three exponents are λ = 1.06 ، λ ₂ = 0 and λ = - 12.7 [18, 19].

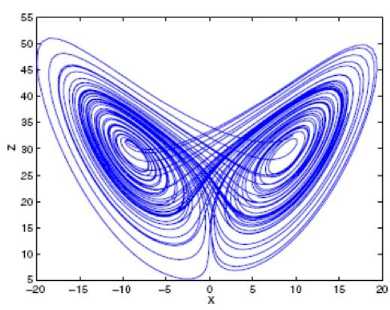
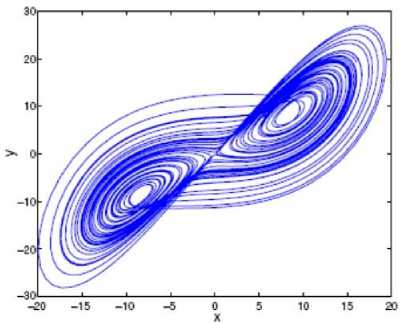
Fig. 2: Lorenz system's lyapunov exponents

According to the Lorenz chaotic system in equation (1), its output has been generated and compared with random values. Figure 3 shows the comparison between random values and Lorenz chaotic output values. As we generated 10,000 random and chaos numbers between 1 and 10; it is obvious the count of each numbers must be 1000 ± α , which the diversity of values in Genetic Algorithm mechanism will be better than if α → 0 . On the other hand, the local convergence that is a disadvantage of traditional the Genetic Algorithm will happen if the value of α is growth.

• IV.    Chaotic Genetic Algorithm

Genetic Algorithm uses random processes in Initial population, Crossover and Mutation process that they can be replaced with chaotic systems such as Lorenz or other chaotic systems such as Hennon map, Logistic map, etc. Pseudo-randomness and ergodicity are two dynamic characteristic of chaotic structures and they are the reason of using chaos systems in Genetic Algorithm instead random processes because they will avoid local convergence. The flowchart of proposed Chaotic Genetic Algorithm has been shown in figure 4; in proposed method we replace random processes in Initial population, Crossover and Mutation with Lorenz chaotic output.

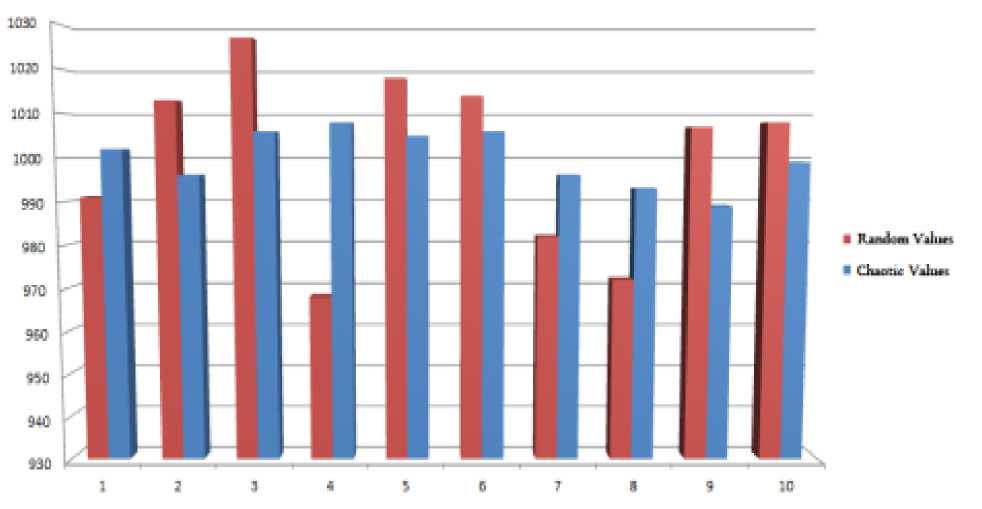
Fig. 3: The frequency charts of 10,000 generated Random and Chaotic numbers

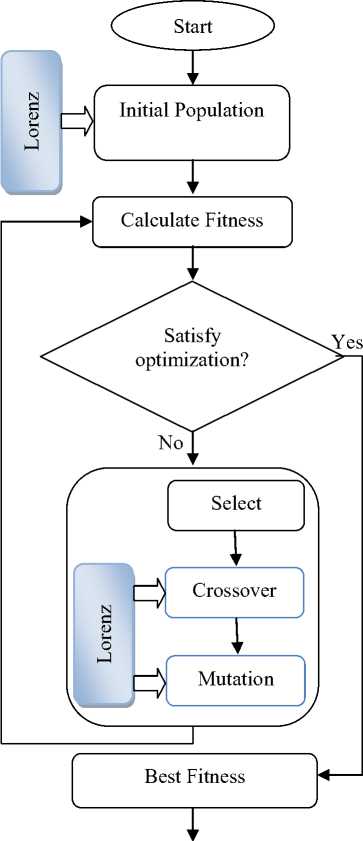
Fig. 4: Chaotic Genetic Algorithm flowchart

• V.    Chaotic Genetic algorithm and Benchmarks

We implement the Chaos Genetic Algorithm based on the Lorenz chaotic system in MATLAB and test on some famous benchmarks such as Schaffer and Clonalg functions. Schaffer is introduced in equation (2) and also we introduce Clonalg in equation (3). These two functions have many good features for optimization problems such as kind of acceptable optimums. These functions have been shown in figure 5.

f ( x , y ) = 0.5

sin ² 7 x ² + y² - 0.5 (1 + 0.001( x ² + y 2 )) 2

x , y e [ - 100,100]

f ( x , y ) = x sin(4 nx ) - y sin(4 ^y + n ) + 1 x , y e [ - 200,200] (3)

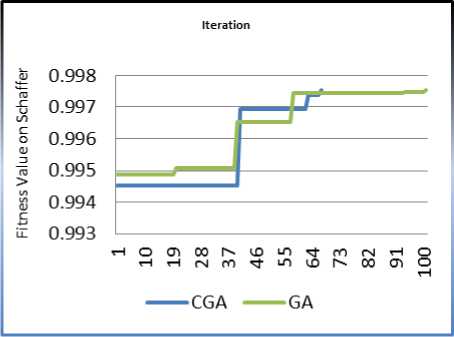
criteria situation in the Genetic Algorithm and proposed Chaos Genetic Algorithm (CGA). Other parameters of Genetic Algorithm such as population size, probability of crossover, etc. have been introduced below. Figure 6 (a) show the results of GA and proposed CGA on the Schaffer function.

• •    Population Size      =  40;

• •    Probability Crossover = 0.6;

• •    Probability Mutation = 0.02;

(a)

(b)

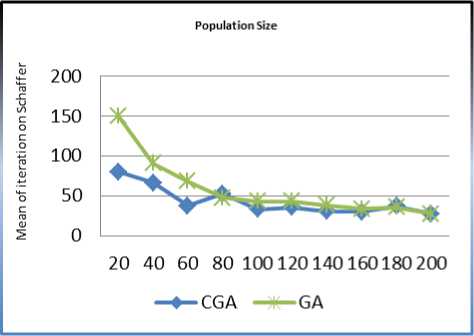
Fig. 6: (a) The GA and CGA criteria satisfaction on Schaffer function, (b) Decreasing of time complexity when Population size is increase

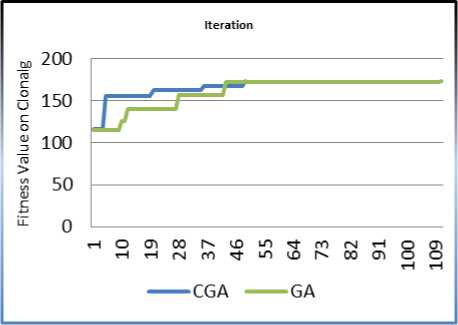
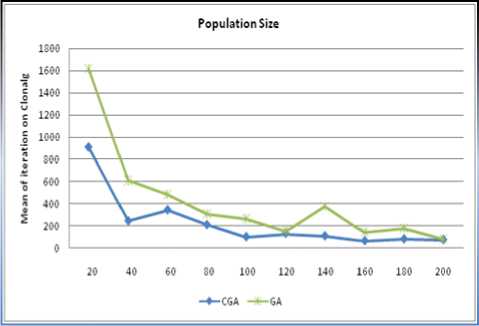
As it is sensible in the Figures 6 and 7, the result of CGA based on Lorenz chaotic system on the Schaffer function is much more efficient than basic GA. The result of time complexity also decreases with increasing population size in GA and CGA. Figure 6 (b) shows the effect of growing population size in GA and CGA on the Schaffer function. We have tested the above method on the Clonalg function and the results were as well as Schaffer function, figure 7 shows my experience on Clonalg function.

The Schaffer function reaches the global maximum value 1 at point (0, 0) but we define 0.9975 as the

(a)

(b)

Fig. 7: (a) The GA and CGA criteria satisfaction on Clonalg function, (b) Decreasing of time complexity when Population size is increase

• VI. Conclusion

In this paper, the Lorenz chaotic system was used instead randomness in the basic Genetic Algorithm. We introduced a hybrid method which uses a chaotic system that can avoid premature convergence. The proposed chaotic system is Lorenz, which is a famous three dimension dynamic chaotic system. The results achieved in this experience show that Chaos Genetic Algorithm is more efficient than the traditional Genetic Algorithm and can converge to the optimum solution rapidly. %34 improvement in Schaffer function and %54 improvement in Clonalg function are two sample results of our method that achieved by Lorenz Chaotic Genetic Algorithm proposed in this paper. The results of our implementation show improving of Chaos Genetic Algorithm instead traditional Genetic Algorithm but there are some other famous chaotic systems such as Henon map, Logistic map, Rossler map, Tent map, Zaslavskii map, etc. that can be used instead Lorenz system and also evaluate their results to find out the most efficient one.

Acknowledgements