Частотная зависимость групповой скорости поверхностных поляритонов в одноосном кристалле типа вюрцита

Поверхностные поляритоны привлекают внимание исследователей и инженеров своими уникальными свойствами и перспективными приложениями в области микро- и наноэлектроники. Поверхностные поляритоны представляют собой коллективные возбуждения, представляющие собой смесь электромагнитной волны и механических возбуждений среды – фононов, распространяющихся вдоль границы среды. Замечательным свойством поверхностных поляритонов является наличие запрещенной зоны, в которой поверхностный поляритон не возбуждается.

В ряде работ [1–3] рассмотрены различные применения поверхностных поляритонов для целей микроэлектроники. В работах [4; 5] проведен анализ возбуждения поверхностных поляритонов с отрицательной групповой скоростью. В работе [7] авторы настоящей статьи представляют результаты расчета параметров распространения и затухания для нанокомпозитов, состоящих из диэлектрической матрицы с распределенными в ней наночастицами. В работе [8] представлен новый тип биосенсора поверхностного плазмонного резонанса, основанный на оптическом датчике с инвертированным градиентным индексом. Отметим работы [9] и [11], в которых авторы анализируют электромагнитные свойства киральных метаматериалов, которые, как и поляритонные среды, проявляют уникальные частотные зависимости электродинамических параметров. В работе [10] представлены результаты расчета угловых спектров отражения света при условии возбуждения поверхностных плазмонов в схеме Кречмана.

В настоящей статье рассматривается задача о возбуждении поверхностных поляритонов в одноосном кристалле типа вюрцита, проводится анализ условий их возбуждения. Особое внимание обращается на расчет групповой скорости поверхностных поляритонов

1. Теоретическое рассмотрение

Рассмотрим условия возбуждения поверхностных поляритонов в одноосном кристалле. На рис. 1 представлена геометрия одноосного кристалла. Оптическая ось кристалла образует угол ϕ с осью Oy .

Обозначим ε значение тензора диэлектрической проницаемости кристалла вдоль оптической оси в главной системе координат, а ε _⊥ – в перпен-

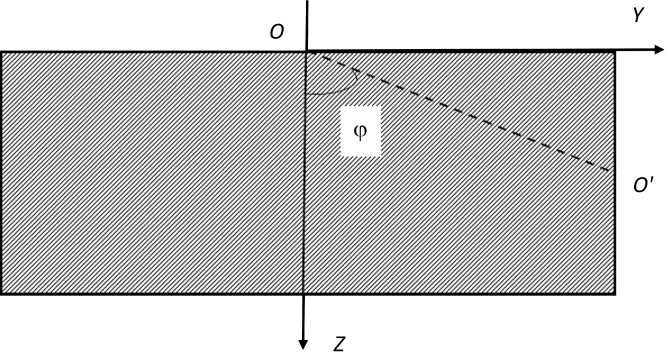
Рис. 1. OO’ - оптическая ось кристалла находится под углом ф с осью Oz Fig. 1. OO’ - the optical axis of the crystal is at an angle ф with the Oz axis

дикулярном направлении. Тогда в лабораторной системе координат YOZ компоненты тензора диэлектрической проницаемости будут иметь вид:

8 _yy = 8_± cos² Ф+ 8| |Sin² ф ;                             (1)

£ _yz = 8 _zy = ( e_±-8| |)sin ф cos ф ;

8 _zz = 8| |COS ф+ 8_± Sin ф .

Область z < 0 занимает изотропный диэлектрик с проницаемостью 8 , а область z > 0 - анизотропный одноосный кристалл типа вюрцита. Проведем анализ возбуждения поверхностных поляритонов для этого случая. Подробные расчеты показывают, что возбуждение распространяющихся поверхностных поляритонов возможно только в случае, когда 8 yz = 0 и для p-поляризации. Вектор магнитной напряженности электромагнитного поля для этого случая имеет только x -составляющую и экспоненциально спадающую зависимость при удалении от границ раздела. В области z < 0 поле имеет вид

H 1 x = H exp ( ^и 1 z ) exp i ( k 0 Пу — ° t ) .             (2)

В области z > 0 поле спадает с расстоянием по закону

^H 2 x = ^H 2 ^eXP ( ^{- k} 0 и 2 z ) expi ( k o ^y -° t ) .            (3)

Процедура получения дисперсионного уравнения для поверхностных поляритонов состоит из 3 шагов. Первый, основанный на волновом уравнении, состоит в нахождении параметров затухания в обеих средах. Второй и третий заключаются в требовании выполнения 2 граничных условий – непрерывности на границе раздела тангенциальных составляющих векторов электромагнитного поля H _x и E _y . Подставляя поля (2) и (3) в волновые уравнения для каждой из сред, легко получим

следующие выражения для параметров затухания и i и и 2 :

^и 1 = V n ^{2 - 8} ;                                         ⁽⁴⁾

^и 2 = ^ ( ⁿ 2 ^-8 zz ) .                            ⁽⁵⁾

V ⁸ zz

Подчеркнем, что оба коэффициента затухания и 1 и и 2 являются положительными величинами.

Условие непрерывности тангенциальных компонент H _x приводит к равенству амплитуд H ₁ и H ₂:

H 1 = H 2 . (6)

Второе граничное условие ведет к одному из самых важных для поверхностных поляритонов равенству:

^ 1 + ^ 2- = 0.                                     (7)

^{8   8} yy

Поскольку три величины и 1 , и 2 и 8 являются положительными, то из (7) следует, что для существования поверхностного поляритона компонента тензора диэлектрической проницаемости 8 yy должна быть отрицательной

Бyy <  0.                                                      (8)

Из уравнения (7) получается дисперсионное

уравнение для поверхностных поляритонов в слу-

чае одноосного кристалла:

n

н =

⁸⁸ zz ( ⁸ yy ^-8 )

⁸ yy ⁸ zz

-

.

Частота поверхностного поляритона находится из условия равенства нулю знаменателя в формуле (9):

⁸ yy ⁸ zz

-

8 2 = 0.

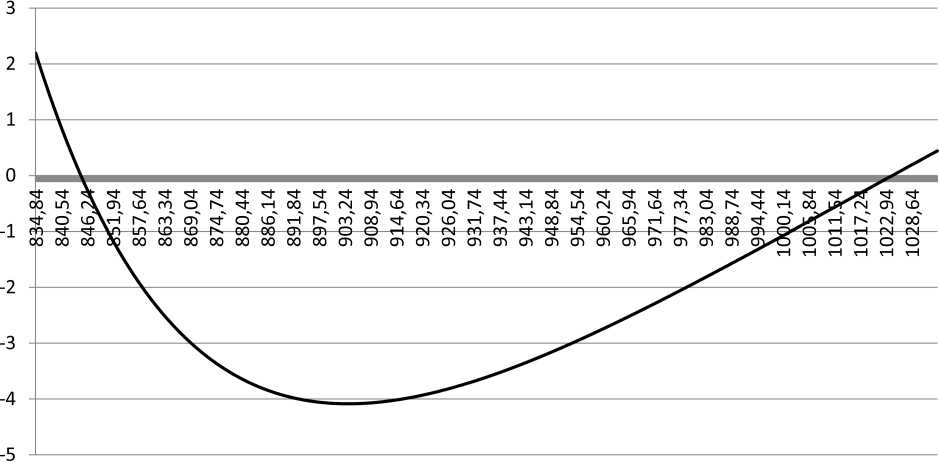
Рис. 2. Частотная зависимость знаменателя в формуле (14). Пересечение кривой с осью абсцисс дает возможные значения частоты поверхностного поляритона

Fig. 2. Frequency dependence of the denominator in formula (14). The intersection of the curve with the x-axis gives possible values of the surface polariton frequency

Далее мы рассмотрим 2 частных случая.

Первый – оптическая ось совпадает с осью z .

Ф = 0 ° .

Тогда имеем:

22 ε ⊥ ( ω ) =ε ⊥ ( ∞ ) ^ω ₂ ^-ω ₂ ^{LO ⊥} ω -ω

ε

⁸ zz = ⁸ Ц ,   ⁶ yy = ⁸ 1 .

( ^ю ) =⁸ ц ^(да)

ω ² -ω ² _LO

ω ² -ω _T ² _O

Дисперсионное уравнение для этого случая

принимает вид

^П 2

⁸⁸ Ц ( ⁶ 1 -⁶ ) 8 ц 8 1 -е ²

Второй – оптическая ось совпадает с осью y .

Ф = 90 ° .

В этом случае имеем:

⁸ zz =⁸ 1 ,    ⁸ yy = ⁸ Ц .

Дисперсионное уравнение для этого случая

принимает вид

2_ ⁸⁸ 1^{( е}ц^{— 8} )

^П ц =          2

⁸ Ц ⁸ 1 ^-8

Заметим, что частота поверхностного поляритона для обоих случаев находится из уравнения

8| 18 1 — 8^ = 0.

Параметры имеют следующие значения: 8₁ ( да ) — — 8,]( да ) = 5,26; го LO ₁₌ 916 см ^{— 1}, го L_{O ||} = 893 см ^{— 1}, ^m TO ₁ = 673 см ^{- 1}, го _{ТО ||} = 660 см ^{— 1}.

На рис. 2 показана зависимость знаменателя в формуле (14) от частоты. Из этого рисунка видно, что кривая пересекает ось абсцисс в двух точках Q 1 = 844,84 см ^{— 1} и Q 2 = 1024,44 см ^{— 1}. Однако детальный анализ показывает, что вторая точка Ω ₂ находится в частотной области, где поверхностный поляритон не существует. Первая же точка отвечает частоте поверхностного поляритона.

На рис. 3 и 4 индекс z отвечает случаю, когда оптическая ось совпадает с осью Oz , а индекс y – когда она совпадает с осью Oy .

На рис. 5 показаны зависимости относительных групповых скоростей поверхностного поляритона от частоты. Здесь VegZ есть групповая скорость в случае, когда оптическая ось направлена по оси Oz , а VegY – вдоль оси Oy .

2. Решение дисперсионного уравнения для кристалла нитрида алюминия AlN. Обсуждение результатов

В модели Лоренца диэлектрические проницаемости данного кристалла описываются функциями [6]:

Заключение

Проведенный анализ показывает, что с увеличением частоты возрастает значение постоянных затухания и постоянных распространения. Рост этот происходит до момента, когда частота достигает

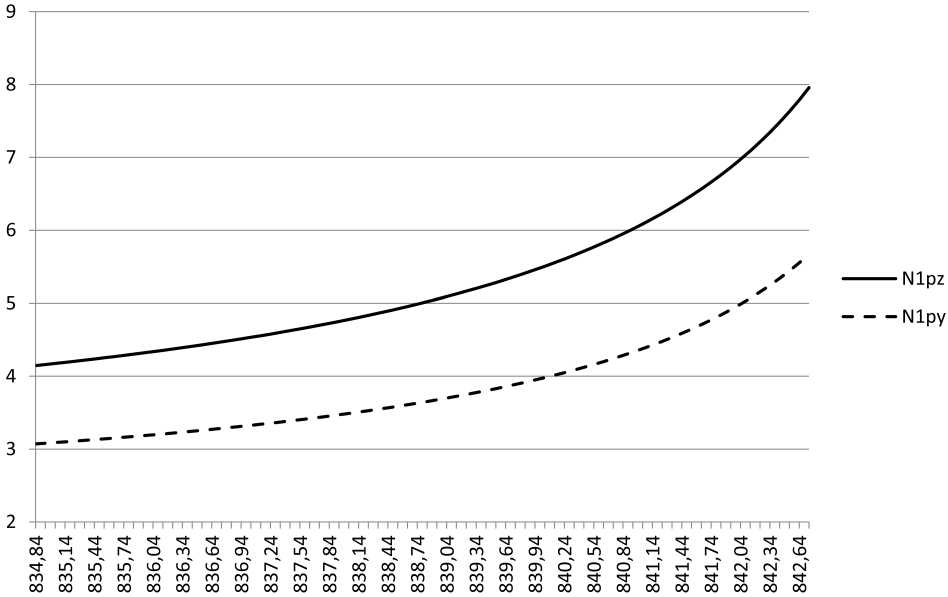
Рис. 3. Частотная зависимость параметров распространения n _{, z} и n _{, y} поверхностного поляритона для двух рассмотренных случаев

Fig. 3. Frequency dependence of the propagation n _{, z} and n _{, y} surface polariton parameters for the two cases considered

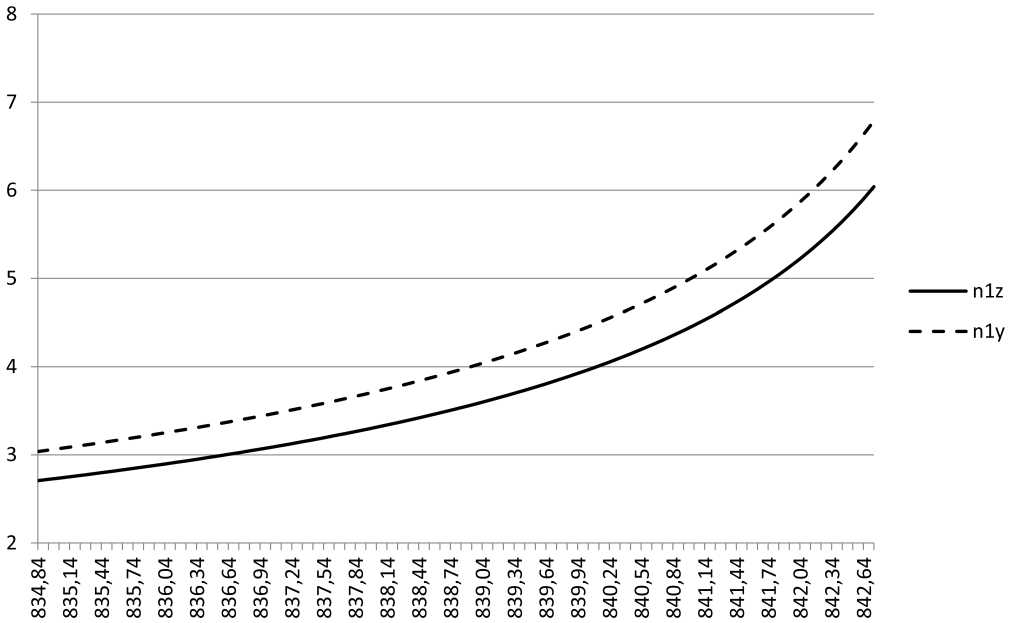
Рис. 4. Зависимость постоянной затухания и 1 для случаев 1 и 2

Fig. 4. Dependence of the attenuation constant и 1 for cases 1 and 2

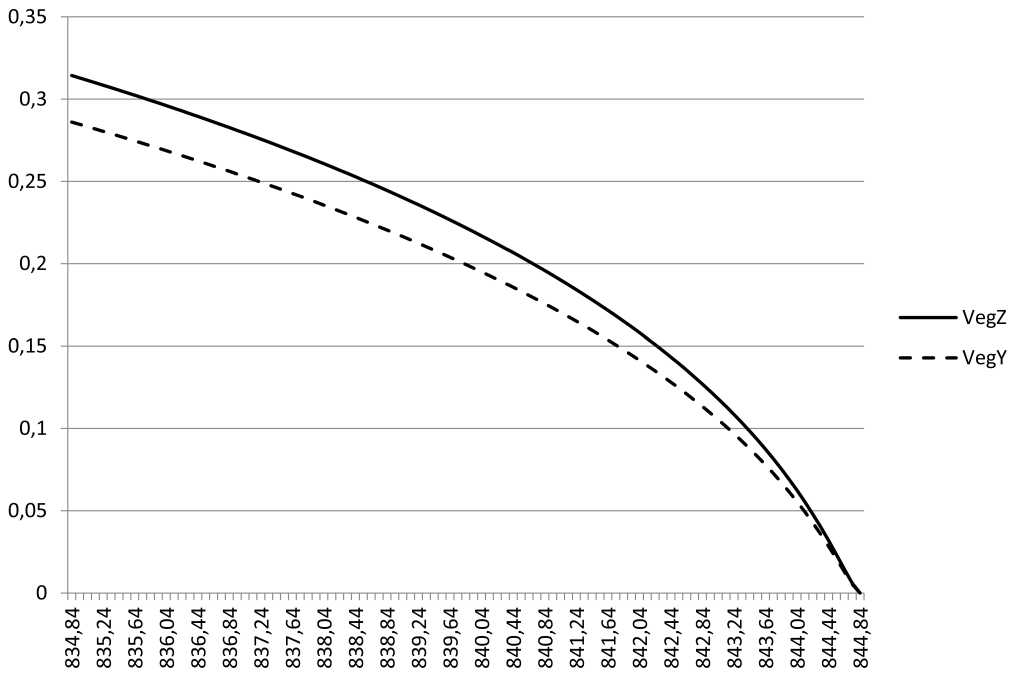
Рис. 5. Зависимость относительных групповых скоростей VegZ/ c и VegY/ c поверхностного поляритона от частоты, c – скорость света

Fig. 5. Dependence of the relative group velocities VegZ/ c and VegY/ c of the surface polariton on frequency, c – speed of light

значения частоты поверхностного поляритона. Поверхностные поляритоны в этом случае одноосного анизотропного кристалла могут возбуждаться только в ограниченной частотной области, когда выполняются условия 8 yy <  0 и (7).

Особый интерес вызывает зависимость групповой скорости поверхностного поляритона от ча- стоты. Из рис. 5 видно, что с увеличением частоты происходит замедление движения поляритона. При достижении частоты значения Q1 - частоты поверхностного поляритона – групповая скорость обращается в ноль. Данное свойство может быть использовано для создания замедляющих систем на основании поверхностных поляритонов.