Частотная зависимость коэффициента поглощения миллиметровых радиоволн в нанокомпозитах на основе опаловых матриц, содержащих наночастицы ферритов-шпинелей

Измерение коэффициентов отражения, прохождения и поглощения волн СВЧ-диапазона важно для нескольких практических приложений. Специальный интерес в этом отношении вызывают фотонные кристаллы [1]. Из литературы известно, что изучаются их свойства как при прохождении электромагнитных волн, так и при отражении. Аналитически и численно исследуется распространение электромагнитных волн в среде с отрицательным показателем преломления [2]. В частности, была решена задача о прохождении волны через пластину такой среды с демонстрацией эффекта фокусировки. Фокусировка осуществляется в ближнем поле излучения в металлизированной фотонной структуре в условиях отрицательного коэффициента преломления. В принципе, если объект сделан из материала с отрицательным коэффициентом преломления, то в идеальном случае он может стать невидимым. Дана общая формулировка задачи взаимодействия электромагнитной волны со стратифицированной средой с отрицательным коэффициентом преломления [3]. Специальное внимание уделяется изучению направленных волн в стратифицированной среде.

Опаловые матрицы считаются одними из наиболее перспективных классов наноматериалов. В настоящее время интенсивно исследуются линейные и нелинейные оптические свойства опаловых матриц, изменения коэффициента преломления, а также вариации интенсивности, поляризации и когерентности, происходящие при прохождения через матрицы мощного когерентного излучения [4]. Наибольший интерес вызывают свойства ансамблей различных микросфер и матриц как фотонных кристаллов. Введение в межсферические пустоты опаловых матриц наночастиц магнитных материалов стало одним из направлений их развития.

Высокочастотные и радиочастотные магнитные свойства ансамблей наночастиц имеют значительную специфику. Применение микроволновых методов исследования представляется эффективным, поскольку последние дают возможность сравнительно просто оценить динамические и релаксационные параметры таких материалов. Опаловые матрицы считаются классом материалов, пригодных для создания сред с отрицательным показателем преломления. Осуществление так называемой «левой» среды с отрицательной действительной частью магнитной проницаемости возможно в области магнитных резонансов. Взаимодействие высокочастотных электромагнитных волн с магнитофотонными кристаллами, рассматриваемыми как метаматериалы, составляет наиболее актуальное направление в этой области. Обращается внимание на прикладные аспекты получения отрицательного показателя преломления на частотах миллиметрового диапазона с использованием явления магнитного резонанса [5, 6]. В [7] выполнен анализ условий существования отрицательного показателя преломления на микроволновых частотах и установлено, что допированные манганиты лантана в области магнитного резонанса являются примером материалов с отрицательным показателем преломления или двойной левой средой. Специальный класс метаматериалов составляют среды с близкой к нулю диэлектрической постоянной или так называемые ENZ (Epsilon-Near-Zero)-материалы. Эффект «сверхсвязи» (supercoupling) представляет один из ярких примеров аномального распространения волн в таких средах [8, 9]. Указанное явление представляет собой туннелирование волны через узкие каналы и изгибы, соединяющие два волновода в условиях, когда обычное прохождение волны невозможно.

В настоящей работе исследуются микроволновые резонансные явления в нанокомпозите, содержащем либо наночастицы никель-цинкового, марганец-цинкового, или кобальт-цинкового ферритов в диэлектрической матрице – решетчатой упаковке субмикронных сфер SiO 2 . Никельцинковый и другие ферриты-шпинели представляются подходящими материалами для заполнения благодаря удачному сочетанию свойств, таких как высокое удельное электросопротивление, малые диэлектрические потери, высокая температура Кюри и химическая стабильность.

Микроволновые свойства измерены на частотах миллиметрового диапазона. Изменения микроволнового сигнала, прошедшего через нанокомпозит, происходят в основном из-за изменения поверхностного импеданса нанокомпозита в условиях магнитного резонанса и из-за поглощения электромагнитной волны в нем. Исследованы магнитные резонансные явления в нанокомпозитах и их влияние на коэффициенты отражения и прохождения через нанокомпозит. В работе показано, что на частотах выше некоторой определенной для каждого материала наночастиц в полях, меньших резонансного, наблюдается еще и антирезонанс, который выражается в максимумах коэффициентов отражения и прохождения. Установлено, что антирезонанс соответствует минимуму коэффициента поглощения.

Анализ результатов ведется с учетом структурного и магнитного состояния материала. Осуществление эффективного взаимодействия микроволновых полей с наночастицами ферритов представляет интерес как для нахождения условий существования отрицательной действительной части магнитной проницаемости, так и для применения в электронных приборах сверхвысоких частот.

Синтез образцов опаловых матриц с диаметрами субмикронных сфер SiO2 от 200 до 350 нм был описан в ряде работ, например в [10]. Нанокомпозиты с внедренными наночастицами никель-цинкового, марганец-цинкового и кобальт-цинкового ферритов были также получены мето- дом пропитки с последующей термической обработкой. Рентгенофазовый анализ показал, что во внесенном веществе большинство рефлексов относятся к фазам типа (NixZn1–x)Fe2O4 и (MnxZn1–x)Fe2O4, имеющим кристаллическую структуру шпинели. На рис. 1 показана структура нанокомпозита с частицами никель-цинкового феррита-шпинели, полученная методом электронной просвечивающей микроскопии. Частицы введенных фаз имеют неправильную форму и размеры от 5 до 70 нм. Объемная концентрация внесенных наночастиц не превышает 3–5 %. В дальнейшем будем называть внедренный материал как феррит, например, никель-цинковый Ni0,5Zn0,5Fe2O4, несмотря на возможное присутствие в нем другой магнитной фазы. Сказанное относится и к нанокомпозитам с марганец-цинковым и кобальт-цинковым ферритами.

Рис. 1. Электронно-микроскопическое изображение структуры нанокомпозита с частицами никель-цинковой шпинели

Магнитные измерения выполнены на установке MPMS-XL фирмы Quantum Design в интервале полей до 50 кЭ и при температурах от 2 до 300 К. Измерены кривые намагничивания и петли гистерезиса, а также температурная зависимость магнитного момента образца в поле напряженностью 10 кЭ. Магнитные свойства массивных образцов ферритов-шпинелей хорошо известны. Такие ферриты выпускаются серийно для целого ряда применений. Однако магнитные параметры опаловых матриц, содержащих наночастицы ферритов, могут существенно отличаться от свойств массивных образцов. Основное внимание в данной работе вызывает область частот и магнитных полей вблизи условий магнитного резонанса. Поэтому наибольший интерес представляет кривая намагничивания нанокомпозитов, поскольку именно величина намагниченности определяет поле магнитного резонанса.

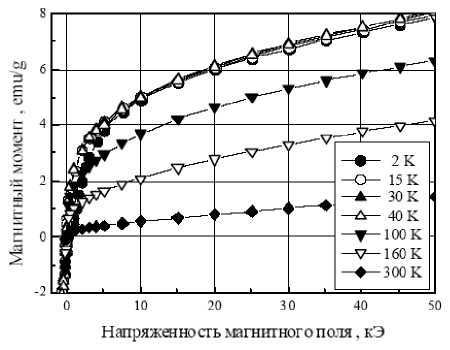
Рис. 2. Кривые намагничивания нанокомпозита с частицами марганец-цинкового феррита Mn 0,5 Zn 0,5 Fe 2 O 4 , измеренные при разных температурах

Кривые намагничивания для образца 3D-нанокомпозита с частицами марганеццинкового феррита Mn 0,5 Zn 0,5 Fe 2 O 4 при нескольких температурах показаны на рис. 2. Кривые намагничивания не имеют полного насыщения в полях до 50 кЭ.

Кроме этого, кривые намагничивания имеют участок быстрого возрастания намагниченности в слабых полях. Указанные особенности кривых намагничивания позволяют сделать заключение, что исследуемые материалы обладают как ферромагнитным (точнее ферримагнитным) упорядочением, так и суперпарамагнитными свойствами. Наличие суперпарамагнитных свойств исследуемых материалов не является удивительным, поскольку частицы внесенных фаз имеют размеры менее 70 нм, а некоторая их часть имеет размеры менее 10 нм.

Микроволновые измерения выполнены в частотном диапазоне 26 - 38 ГГц с использованием прямоугольных резонаторов и стандартных волноводов, работающих на моде TE 10 . Для выполнения микроволновых измерений образец помещался в волновод (рис. 3, а) или в прямоугольный резонатор (рис. 3, б). При этом образец длинной стороной размещался вдоль оси СВЧ-тракта при размещении в резонаторе и поперек тракта при размещении в волноводе. Внешнее постоянное магнитное поле H , создаваемое электромагнитом, прикладывалось перпендикулярно волновому вектору волны q . В случае, когда образец находится в волноводе, внешнее магнитное поле лежит в плоскости образца либо параллельно, либо перпендикулярно вектору микроволнового электрического поля E ~ . Вектор H в этих случаях будет либо перпендикулярен микроволновому магнитному полю H ~ , либо будет лежать в плоскости H ~ соответственно. Во всем интервале частот осуществляется одномодовый режим. Для выполнения микроволновых измерений образец толщиной 1 мм помещался в волновод сечением 7,2×3,6 мм. Все микроволновые эксперименты выполнены при комнатной температуре.

Необходимость использования двух методик измерения микроволновых характеристик обусловлена следующими обстоятельствами. В резонаторе возможно выполнить измерения на частотах вблизи резонансных частот резонатора, каждая из которых соответствует определенной структуре электромагнитных полей. Резонатор включен в СВЧ-тракт каскадно. В условиях магнитного резонанса резко увеличивается поглощение электромагнитной энергии; полевая зависимость амплитуды принятого сигнала определяется резонансной зависимостью мнимой части магнитной проницаемости образца от напряженности внешнего постоянного магнитного поля. Вторая методика, в которой образец помещается в поперечное сечение волновода, имеет достоин- ство в том отношении, что частота волны может изменяться непрерывно во всем интервале, в котором распространяется волна TE10. Два варианта расположения вектора внешнего постоянного магнитного поля (варианты (а) и (б) на рис. 3, а) дают возможность реализовать различную ориентацию полей и выявить разные типы резонансов.

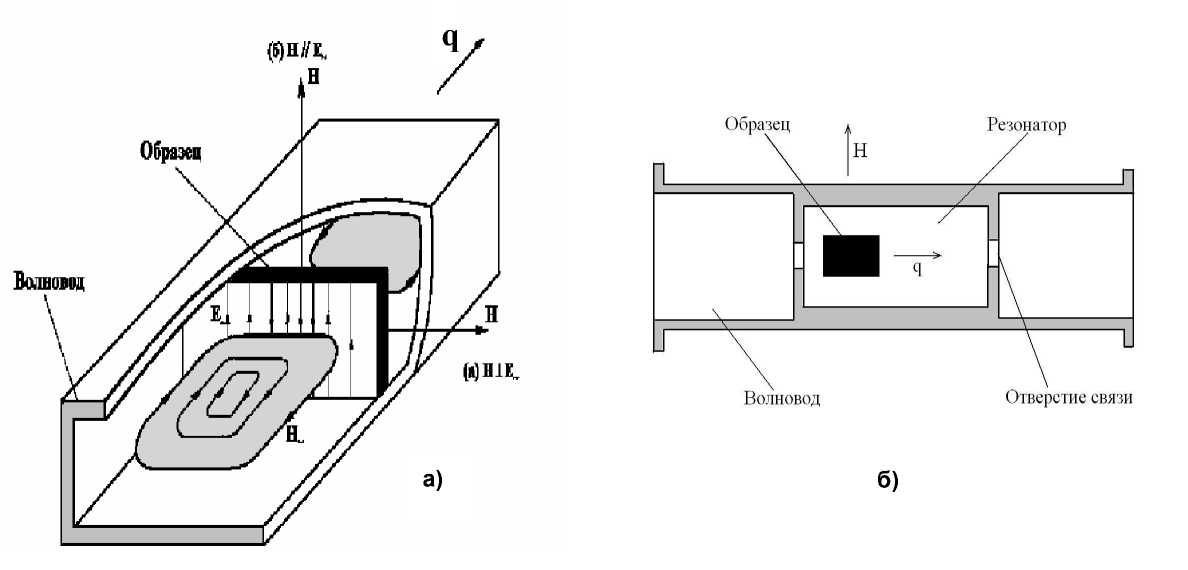
Рис. 3. Схема расположения образца в волноводе (а) и в резонаторе (б)

В микроволновых экспериментах с помощью измерителя КСВ и отражения Р2-65 измерялись модули коэффициентов прохождения D и отражения R . Влияние внешнего постоянного магнитного поля на коэффициенты оценивалось относительным изменением во внешнем магнитном поле модуля коэффициента прохождения d m = [ | D ( H) | - | D (0) | ] / 1 D (0) | и относительным изменением модуля коэффициента отражения r m = [ | R ( H) | - 1 R (0) | ] / | R (0) | , где D ( H), R ( H) - коэффициенты прохождения и отражения от образца, измеренные в поле H .

Целью проведенных микроволновых измерений с нанокомпозитами с частицами ферритов-шпинелей было установление типов магнитных резонансов, которые могут осуществляться в магнитных нанокомпозитах на основе опаловых матриц. Резонатор был включен в СВЧ-тракт каскадно, как это показано на рис. 3, б. При помещении образца в резонатор резонансные частоты уменьшаются, ширина резонансной линии увеличивается из-за микроволновых потерь в образце. Результаты измерения полевой зависимости амплитуды микроволнового сигнала для нанокомпозита с частицами Mn 0,5 Zn 0,5 Fe 2 O 4 показаны на рис. 4. Наблюдается одна широкая линия магнитного резонанса.

Аналогичные измерения были выполнены с нанокомпозитом, содержащим частицы никельцинкового феррита-шпинели Ni0,5Zn0,5Fe2O4, на нескольких собственных частотах резонатора. Результаты измерений приведены на рис. 5. На всех частотах в полях свыше 10 кЭ зарегистриро- вано резкое уменьшение прошедшего сигнала, связанное с магнитным резонансом в наночастицах феррита-шпинели. Однако поля в 12 кЭ оказалось недостаточно, чтобы достигнуть резонанса.

Тем не менее, измерения показали, что изменения микроволнового сигнала в области резонанса велики, они достигают 50–60 %. Уменьшение прошедшего сигнала следует связать с диссипацией, вызванной увеличением мнимой компоненты эффективной магнитной проницаемости. Можно отметить, что в полях, меньших резонансного, наблюдается некоторое увеличение прошедшего сигнала. Оно вызвано уменьшением поглощения в области полей, соответствующих переходу действительной части проницаемости через нуль, то есть в области антирезонанса.

Измерения в волноводе были выполнены по схеме, показанной на рис. 3, а. Как правило, использовалась конфигурация полей HLH ~ как более информативная. Сопоставление резуль-

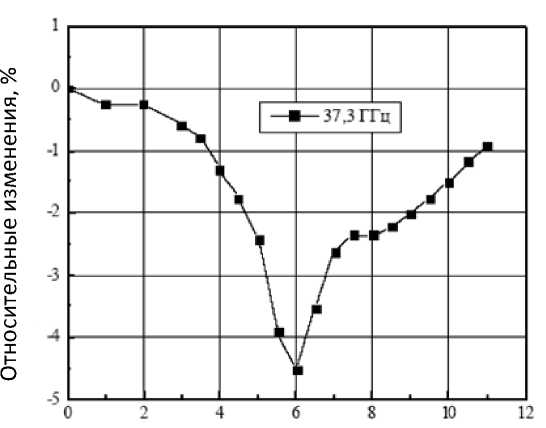
Магнитное тюле. кЭ

Рис. 4. Магнитный резонанс в опаловой матрице, содержащей марганец-цинковый феррит Mn 0,5 Zn 0,5 Fe 2 O 4 , измерения в резонаторе

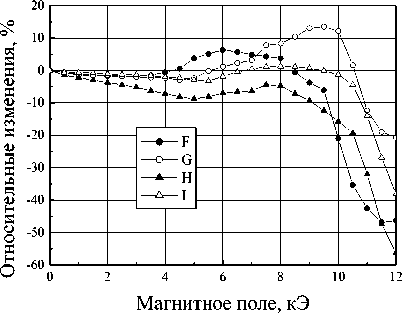
Рис. 5. Полевые зависимости микроволнового сигнала, прошедшего резонатор с образцом, содержащим наночастицы Ni 0,5 Zn 0,5 Fe 2 O 4

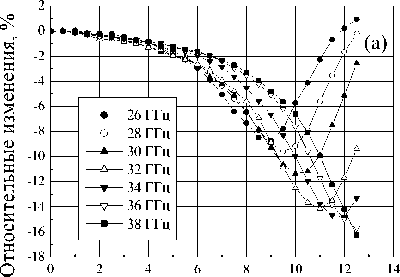
татов измерения полевой зависимости коэффициентов прохождения и отражения для нанокомпозита, содержащего частицы кобальт-цинкового феррита Co 0,35 Zn 0,65 Fe 2 O 4 , проведено на рис. 6. Полученные зависимости, измеренные на частотах до 30 ГГц, оказались похожи друг на друга как по величине изменений, так и по форме зависимости. На этих зависимостях присутствует только уменьшение коэффициента прохождения, вызванное резонансом. На более высоких частотах характер зависимостей становится несколько различным. Если на полевой зависимости прошедшего сигнала, по-прежнему, присутствует только резонансное уменьшение прошедшего сигнала, то в отраженном сигнале в полях, меньших резонансного, наблюдается максимум коэффициента отражения.

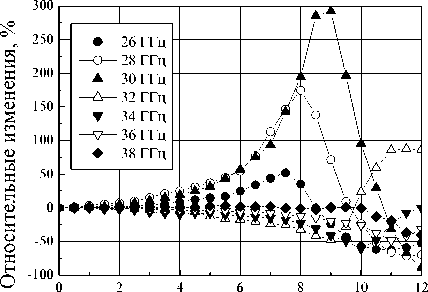
Полевые зависимости изменений отраженного сигнала для образца, содержащего наночасти-

цы никель-цинкового феррита, при HLH ~ показаны на рис. 7. Обращают на себя внимание очень большие, до 4 раз, изменения отраженного сигнала в максимуме, которые можно назвать гигантскими. Уменьшение сигнала в резонансе визуально на рис. 7 кажется менее значительным, но в действительности оно достигает –90 %. Другими словами, в области резонанса отраженный сигнал уменьшается в 10 раз.

Рассмотрим прохождение и отражение волн от слабопроводящего ферромагнитного образца, помещенного в прямоугольный волновод. Полагаем, что выбран такой интервал частот, что в волноводе может распространяться только мода TE 10 . Длина образца вдоль оси волновода равна d , поперечные размеры волновода a и b , причем a – это большая стенка волновода . Образец полностью занимает поперечное сечение волновода, как показано на рис. 3, а. Заполненный образцом участок волновода – область 2 – имеет эквивалентное сопротивление Z 2 , а незаполненные участки – сопротивление Z 1 . Обозначим через β 2 комплексную постоянную распространения, β 2 = в ' 2 + ie" 2 . Комплексные коэффициенты прохождения D и отражения R выражаются следующими формулами из [11]:

D =------------ / 1 - \ ,

chp2 d +1 (^ + ^ 1) shp2 d

R_    2 (^ ) shP2 d

= ch p ₂ d + ¹ (^^{- 1} ) sh p ₂ d ’

где ξ = Z 2 / Z 1 .

Магнитное поле , кЭ

а)

Рис. 6. Полевые зависимости относительных изменений коэффициента прохождения (а) и коэффициента отражения (б) для нанокомпозита, содержащего частицы Co 0,35 Zn 0,65 Fe 2 O 4 (толщина образца 1 мм)

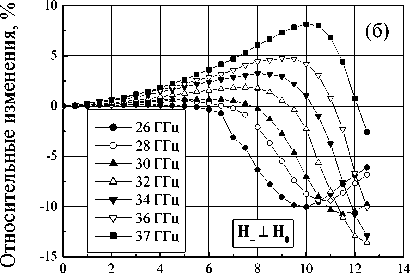
Магнитное поле , кЭ б)

Эквивалентные сопротивления для основной моды волновода TE₁₀ можно выразить через волновые сопротивления W 1 и W 2 [12]:

~ кb    _ кЬ

Z 1 = ^{π b}W 1 ; Z 2 = ^{π b}W 2 , 2 a 2 a

—

/ Г Г 2 - 2 1 2

где W 1 = 120 π

; W ₂ = 120 πμ _ef

.

Здесь ε ef , μ ef – некоторые эффективные диэлектрическая и магнитная проницаемости, c – скорость распространения электромагнитных волн в вакууме. Отметим, что в рассматриваемом случае нанокомпозит со включениями металла не может рассматриваться как хороший проводник, поскольку глубина скин-слоя (4–5 мм на рассматриваемых частотах) значительно больше толщины образца 1 мм. Поэтому можно считать, что в наших экспериментальных условиях скин-эффект в распределении электромагнитного поля проявляется слабо. Малость размеров включений (10–80 нм) по сравнению с глубиной скин-слоя дает возможность использовать приближение однородной среды с эффективными проницаемостями.

Одной из основных целей данной работы является установление условий наблюдения и физической природы максимумов коэффициента отражения и прохождения. Ранее при изложении экспериментальных результатов было показано, что максимумы наблюдаются на частотах, превышающих некоторое значение. Сопоставление данных, полученных для 3D-нанокомпозитов с частицами разных ферритов, например, Ni0,5Zn0,5Fe2O4 и Ni0,35Zn0,65Fe2O4 или Co0,5Zn0,5Fe2O4 и Co0,35Zn0,65Fe2O4, показало, что величина этой частоты различна в каждой паре нанокомпозитов. При изложении результатов микроволновых измерений было высказано предположение, что максимум в коэффициенте отражения соответствует антирезонансу. Если это действительно так, то в явлении должны присутствовать две характерные черты: 1) максимум отражения наблюдает- ся в области полей, где действительная

• 2)    максимум коэффициента отражения соответствует минимуму поглощенной

  мощности в композитов зависимости хождения и

  
  

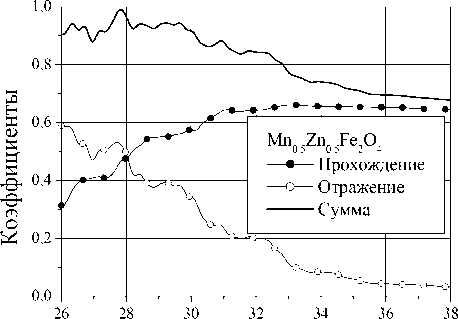
образце. На образцах нано-были измерены частотные модулей коэффициентов проотражения. Результаты для нанокомпозита, содержащего частицы марганец-цинковой шпинели Mn0,5Zn0,5Fe2O4, показаны на рис. 8.

Коэффициент прохождения с ростом частоты в целом увеличивается, а коэффициент отражения – уменьшается. Численные значения коэффициентов на рис. 8 даны по мощности. На каждой частоте это D ( H = 0) и R ( H = 0). Видно, что в исследованном частотном интервале эти коэффициенты одного порядка по величине.

часть магнитной проницаемости меняет знак;

Магнитное поле , кЭ

Рис. 7. Полевая зависимость коэффициента отражения для нанокомпозита, содержащего частицы Ni 0,5 Zn 0,5 Fe 2 O 4 (толщина образца 2 мм)

То же зафиксировано для всех изученных нанокомпозитов. На рис. 8 приведена также и частотная зависимость суммы этих коэффициентов. Разность 1 - [ | D | +| R | 1 выражает долю поглощенной мощности. Ее можно выразить в децибелах и отнести на 1 мм толщины образца. Получится значение коэффициента поглощения в нулевом магнитном поле. Относительно этого значения можно отсчитывать изменения в магнитном поле. То есть для каждого значения поля H вычислять разность 1 - [ | D ( H )| + | R ( H )| ] и выражать ее в дБ/мм. Результат для нанокомпозита с частицами Ni 0,5 Zn 0,5 Fe 2 O 4 показан на рис. 9. На более низкой частоте на зависимости присутствует один максимум поглощения. Он реализуется в поле H ≈ 9 кЭ и соответствует магнитному резонансу. На более высокой частоте 36 ГГц максимуму поглощения предшествует минимум. Он наблюдается в поле H ≈ 10,5 кЭ.

Частота, ГГц

Рис. 8. Частотные зависимости модулей коэффициентов прохождения и отражения по мощности, а также их суммы для 3D-нанокомпозита, содержащего частицы Mn 0,5 Zn 0,5 Fe 2 O 4

Проведенный анализ позволяет понять, почему экспериментально измеренные полевые зависимости коэффициентов отражения и прохождения на рис. 9, 10 на низких частотах имеют сходный вид. В рассмотренной области миллиметровых волн значения этих коэффициентов, измеренные без внешнего магнитного поля, имеют один порядок величины, |D(0)| = |R(0)|. Резонансный вид экспериментально измеренных зависимостей dm(H) и rm(H) обусловлен тем, что компоненты тензора магнитной проницаемости ц и ца при выполнении условий магнитного резонанса получают добавки, резонансным образом зависящие от напряженности магнитного поля. Соответственно резонансные добавки получат постоянная распространения β2 и отноше- ние импедансов ^. Резонансные добавки вызваны поглощением волны в условиях магнитного резонанса, поэтому на полевых зависимостях коэффициентов прохождения и отражения наблю- дается минимум.

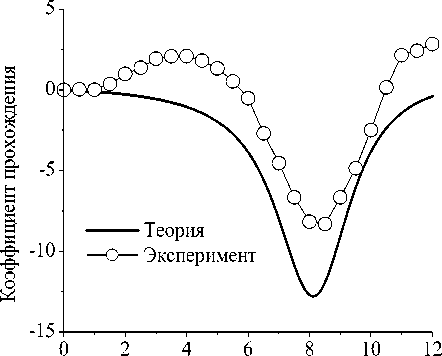
Магнитный резонанс соответствует минимуму коэффициента прохождения. На рис. 10 положение минимумов для расчетной и экспериментальной зависимостей близкое и приходится на область Н= 8,2...8,4 кЭ. На экспериментальной зависимости при полях, меньших поля резонанса, наблюдается максимум коэффициента прохождения, который соответствует минимуму поглощения волны, а именно антирезонансу. На частоте 26 ГГц положение максимума приходится на поле H = 3,9 кЭ. На расчетной зависимости антирезонанс отсутствует, поскольку в использованном для расчета простом варианте теории последний не может быть получен. Для правильного описания антирезонанса требуется использовать метод расчета, предполагающий существование в проводящем ферромагнетике нескольких (трех) собственных волн. Кроме того, нужно осуществить корректный учет условий закрепления спинов на границах образца. Столь подробный расчет представляет самостоятельную сложную задачу и выходит за рамки данной статьи.

Сопоставим поле антирезонанса, за которое примем поле максимума на полевой зависимости коэффициента прохождения и поле H2 , в котором действительная часть магнитной проницаемости обращается в нуль; Re(ц) = 0. Согласно [13] зависимость поля H2 от частоты задается соот- ношением

H2 = (to/у)2 +(2пM)2 - 2пM .

При f = 26 ГГц H 2 = 4,13 кЭ, что близко к экспериментально наблюдаемому значению поля для максимума 3,9 кЭ. В области от поля антирезонанса резонанса 3,9 кЭ до поля резонанса H = 8,5 кЭ действительная часть магнитной проницаемости отрицательна. Отсюда следует, что наблюдаемый экспериментально максимум в коэффициентах прохождения и отражения действительно приходится на значение внешнего поля, в котором действительная часть магнитной проницаемости меняет знак. Зависимости действительной и мнимой частей эффективной магнитной проницаемости от напряженности магнитного поля, измеренные на частоте 26 ГГц в нанокомпозите с частицами никель-цинкового феррита, показаны на рис. 11.

В целом, в данной работе изучены электромагнитные свойства 3D-нанокомпозита на основе опаловой матрицы с внедренными в межсферические пустоты наночастицами ферритов-шпинелей. Экспериментально продемонстрировано эффективное взаимодействие электромагнитных волн с 3D-нанокомпозитами. В миллиметровом диапазоне изменения коэффициентов прохождения через пластину нанокомпозита и отражения от нее вызваны двумя физическими явлениями – магнитным резонансом и антирезонансом. Установлено, что спектры магнитного резонанса содержат акустическую ветвь.

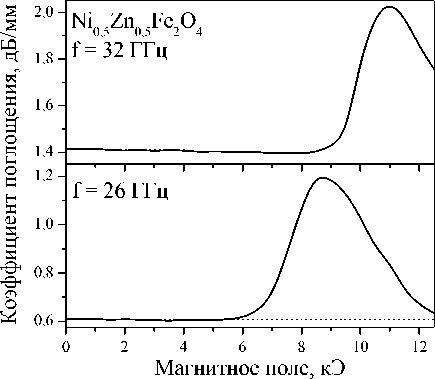
Рис. 9. Полевые зависимости коэффициентов поглощения для нанокомпозита с частицами никель-цинкового феррита Ni 0,5 Zn 0,5 Fe 2 O 4 на частотах 26 ГГц и 32 ГГц

Магнитное поле, кЭ

Рис. 10. Зависимости относительного изменения модуля коэффициента прохождения от напряженности магнитного поля

Измерена частотная зависимость коэффициентов прохождения и отражения от нанокомпозитов при отсутствии внешнего магнитного поля. Было установлено, что в диапазоне частот от 26 до 38 ГГц коэффициент отражения в целом убывает, а коэффициент прохождения в целом возрастает при увеличении частоты волны. Разработан алгоритм расчета зависимости коэффициента прохождения от напряженности внешнего постоянного магнитного поля. Сопоставление расчетной и экспериментальной зависимостей показало, что в области магнитного резонанса, осуществляется разумное соответствие приведенных зависимостей.

Полученные результаты создают предпосылки для разработки управляемых магнитным полем высокочастотных устройств, ра-

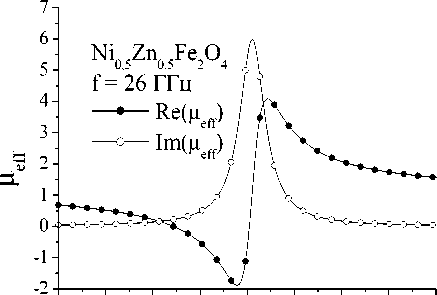
-1,00 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 1,00

(H-H1)/H 1

Рис. 11. Действительная и мнимая части магнитной восприимчивости нанокомпозита с частицами Ni 0,5 Zn 0,5 Fe 2 O 4 , измеренная на частоте 26 ГГц

бота которых будет основана на использовании микроволнового магнитного резонанса в магнитных нанокомпозитах на основе опаловых матриц. Такие устройства конструктивно достаточно просты и могут быть весьма эффективны в работе. В работе установлено, что для получения наи-

больших изменений микроволнового сигнала следует осуществлять ориентацию полей H ⊥ H_~ . Рассматриваемые материалы могут найти применение при создании управляемых аттенюаторов, фазовращателей и других устройств миллиметрового диапазона.

Работа выполнена при частичной поддержке проекта 12-М-23-2052.