Частотное уравнение для балки Тимошенко с упруго прикреплённым телом с двумя степенями свободы

В работе [1] рассматривалась механическая система (рис.1), состоящая из твердого тела с двумя степенями свободы, прикрепленного с помощью двух пружин к балке Тимошенко.

Рис. 1. Механическая система «упругая балка с телом, установленным

на двух пружинах»

Для данной системы на основании вариационного принципа Гамильто-на-Остроградского построена математическая модель в виде гибридной системы дифференциальных уравнений mz + c1( z - d 1ф - u (a1, t)) + c 2 (z + d 2ф - u (a 2, t)) = 0,

1фф - c, d 1(z - d 1ф - u(a1, t)) + c2d2 (z + d2ф - u (a2, t)) = 0, d4u(x,t)     d3e(X,t)     /■u(x,tК пвP(x,tk

EI----1--EI ----i-- P I ---э— V + P I -----} +

5 x⁴            5 x³           5 x ²d t²          5 x 5 t²

+ p F ^{d u (} x • tt d t ²

= c/ z - d ₁ ф - u ( x , t )) 5 ( x - a j +

+ c ₂ ( z + d₂ ф - u ( x , t )) 5 ( x - a ₂ ),

EI d ^ u^x^t) - ei 9^{2e (} x , t ) - p i 5 ³ и ⁽ xt ) + p i 9^{2e (} x , t ) + x Gp p (x , t ) = 0,

I      d x ³             d x ²            d x 9 1 ²            d t²

где m , c j , c 2 , d , , d 2 , 1 ф , E . I , p , F ,

d ² u ( x , t ) dt²

, a j , a 2 , X , G , F

- параметры сис

темы [1]; z, ф - соответственно поступательное и угловое отклонения тела; u(x, t) - поперечное смещение точек балки c координатой x в момент времени t; в(x, t) - угол сдвига.

Решение системы (1) понимается в обобщенном смысле [1].

На функции u ( x , t ) и в ( x , t ) наложены некоторые граничные условия, соответствующие условиям закрепления на концах балки:

Г , ( u (0, t ), в (0, t )) = 0,       Г ₂ ( u ( l , t ), в ( l , t )) = 0.                       (2)

В данной статье для механической системы, описываемой гибридной системой дифференциальных уравнений (1) с краевыми условиями (2) производится построение частотного уравнения.

получим алгебраическо-дифференциальную систему уравнений (3) относительно амплитудных параметров системы Z , Z , , V ( x ), B ( x ):

— тА ю ² + C j ( Z — d j Z , — V ( a j )) + c 2 ( Z + d 2 Z , — V ( a 2 )) — 0,

— IvAv®2 — cj d j(Z — dj Z, — V(aj))+ c 2 d 2(Z + d 2 Z, — V(a 2))— 0, d4 V(x) - d3B(x) рю2 d2 V(x) - рю2 dB (x) - pFю2 V( ) _ dx4     dx3     E dx2 E dx EI

— -^ (Z — dj Z, — V (x )Ж x — aj) + -2- (Z + d 2 Z, — V (x ))5( x — a 2), EI                       EI d 3V (x) . dx3

2 +— - B ( x ) + X GF B ( x ) — 0. dx ²     E dx E        EI

Отметим, функции V ( x ) и B ( x ) удовлетворяют граничным условиям соответствующим граничным условиям (2), накладываемым на функции u ( x , t ) и в (x , t ):

Y j ( V (0), B (0)) — 0,       у 2 ( V ( l ), B ( l )) — 0.

В работе [j] была доказана следующая теорема.

Теорема 1. Если вектора Z, Z,, функции V(x) и B(x) удовлетворяют алгебраическо-дифференциальной системе уравнений (3), функции V(x) и B(x) граничным условиям (4), то для функций V(x) и B(x) справедливо представление

V ( x ) — G j( x — a j ) |b( Z — d j Z , — V ( a j )) + G 2( x — a 2 )   ( Z + d 2 Z , — V ( a 2 )),

<                 EI                             EI(5)

cc

B (x) — Bj( x — aj) -^( Z — djZ, — V (aj)) + B2( x — a 2) -2- (Z + d 2 Z, — V (a 2)), I              EIEI где функции Vi (x), Bi (x), (i — j, 2) являются обобщенными решениям сис- темы d4Gi(x)  d3Bi(x)  рю2 d2Gi(x)  рю2 dBi(x)  pF®2

G , ( x ) — 5 ( x ),

B.( x ) — 0,

---------------;---;--1--------- dx4 dx3 E dx2     E dx EI

d³ G ( x ) d ² B ( x ) р ю ² dG ( x ) р ю ²        % GF

------+  --—  ----B, (x) +  ---- dx3      dx2     E dx E         EI с краевыми условиями

Y j ( G , ( — a , ), B , ( — a , )) — 0,       у 2 ( G , ( l — a , ), B , ( l — a , )) — 0.        (7)

Требуется определить условие, из которых находятся частоты иг, при которых существует решение алгебраическо-дифференциальной системы уравнений (3) с краевыми условиями (4). Заметим, что найденное условие и будет уравнением собственных частот (частотным уравнением) исходной системы, описываемой гибридной системой дифференциальных уравнений (1) с краевыми условиями (2).

• 2.    Частотное уравнение

Исключим из системы (6) переменные Bi (x). Для этого продифференцируем второе уравнение из (6) и отнимем от него первое уравнение системы (6). Полученное соотношение dBi (x) _ pro'

—

dx

X G

G , ( x ) — -^ ( x )

i X GF

подставим в первое уравнение (6). В результате получим d4 Gi( x)

dx ⁴

Л 2

^ +

p ro ² I d ² G ( x )

—

pro

V x G   E

dx ²

pro-—STOL) g (x)= xGE   EI J

X GFE

5 ( x ) —

1 d² 5 (x ) X GF dx x

Заметим, решение уравнения (9) понимается в обобщенном смысле. Если Gi (x) некоторое обобщенное решение уравнения (9), то при любой функции p(x) из класса основных функций должно выполняться тожде- ство

fz

0 i =1 V

d ⁴ G ( x )

dx ⁴

=U E -

—

p ro ² p ro ² I d ² G i ( x )

• -^L | ₅( x ) X GFE J

E J dx x

—

/24   77 2 A A p ro pFro I z x,

—— — I G ^{( x} ) P i ^{( x} ) ^dx =

(X GE EI ) J

1 d²8{x ) X GF dx x

p i ( x ) dx .

Используя правило дифференцирования обобщенных функций [2] представим последнее выражение в виде

• l-    ² < d ⁴ G i (x )

fz

0 i =1 V

dx ⁴

p ro ² p ro ² | d ² G i ( x )

x G E J dx ²

=Z 1

—

• -^ro L I p (0) — d!p i I2) X GFE J       x GF dx ²

• 2,4         , 2 AA

p ro    pF ro I

——--— I G ^{( x} ) P i ^{( x} ) dx =

XGE   EI )

J     J

Таким образом, в дальнейшем будем понимать для обобщенного решения уравнения (9) выполнение тождества (10).

Теорема 2. Обобщенное решение уравнения (9) определяется выражением

G ( x ) = 1

p ro ² I G ₍ x ) 1_ d² G ( x ) X GFE ^{J iA J} x GF dx ² ,

где функция Gi (x), (i = 1,2) являются обобщённым решением уравнения d4 Gi( x) + dx4

+ p ® ² J d² G ( x ) +

E J dx ²

⁴ p²® ⁴ pF ®² _v X GE ^- n

G i ( x ) = 5 ( x ).

Доказательство . Подставив (11) в левую часть выражения (10), после преобразований получим

* ^{2 4} d ⁴ G ( x )

о i = i V

dx ⁴

⁴ p ® ² + p ® ² 1 d ² G ⁽ x )

_V X G E ^J dxx

4 p ² ® 4

V X GE

pF— I G i( x ) V i( x ) dx = EI J

=111

p ® ²

X GFE

V dx ⁴

4 p ® ² + p ® ² 1 d ² G i ( x )

_V X G "T ^J dxx

p² ® ⁴ "GEE

pF®2

EI

G i (x ) 9 i (x ) dx -

Гу f 1 d ² 4 d ⁴ G ( x ) ¹ И V x GF dx ² V dx ⁴

⁴ p ® ² + p ® ² 1 d ² G ⁽ x )

_V X G E J dxx

p ® - pF ® I G ( x )

Ф _i ( x ) dx

-E 1

p ® ²         r \    1 d²5 ( x ))     Y

X GFE J ^{5 ( x} M ^{( x} ) ^- _{x GF} dx 2 Ф i ^{( x} ) J dx =

2 ((

= И ¹ i = i Vv

p ® ² I

1 d M (0) "

XGF dx2 v что совпадает с правой частью (10). Теорема доказана.

Замечание 1. Решение уравнения (9) удовлетворяет некоторым крае- вым условиям

; % , ( G ( - a^,B i ( - a i )) = 0,       ) % 2 ( G ( l - a i ), B i ( l - a i )) = 0,        (13)

соответствующим краевым условиям (7) системы (6).

Решение уравнения (12) можно найти в виде суммы общего решения однородного уравнения d4 G( x)+4 p®2+p®21 d2 Gi( x)+4 p2®4 dx4    V xG   E J dx2    V xGE pF®- J G,( x) = 0 (14)

EI J

и фундаментального решения уравнения (12). Отметим [3], в качестве фундаментального решения (12) можно взять решение однородного уравнения (14), удовлетворяющее начальным условиям

G(0) = 0, dG (0) = 0, d^GG (0) = 0, d-GG (0) = 1, dx dx         dx умноженное на функцию Хэвисайда 6(x).

При предположении

pF® +p® 1

V X GF   E J

(  2  4           2

p ® pF® -

V X GE   EI

> 0,

общее обобщенное решение уравнения (12) найдется в виде

2 .     2

e + ц ^ ц

shцx sin ex

e 7

,

где

PF to 2 P to to xGF + E +4	f       2         2 A2 PF to_ + P toL I — 4 • ( x GF E J	Г „ 2 4          2 A P to PF to I ( x GE EI J
2

,

—

pFto to xg

—

^ pF to ²

P to +

E Я X GF

2 V

E 7

P 2to4 PFto1

—

( X GE EI

.

V ( x ) = 1

—

—

1 d ² G 1 ( x — a 1 ) x GF   dx¹

1 — j^_ I g ( x — a )

x GFE J ^{2    2}

1 d ² G ₂ ( x — a ₂ ) x GF   dxx

сМ. Z — d Z , — V ( a ₁ )) +

EI

( Z + d 2 Z , — V ( a 2 )).

EI

Подставив последовательно в соотношение (15) x = a i , i = (1,2), получим систему вида

V ( a , ) = 1

—

d ^{2 G 1(0) 1} |L( Z — d 1 Z , — V ( a j) + EI

x GF dx x

¹              I ^G 2 ^{( a} 1 a 2 )

xGFE 7

1 d ² G ₂ ( a 1 — a ₂ ) x GF dx x

• -E ( Z + d 2 Z, — V ( a 2 )) EI

V ( a ₂ ) =    1

P to ²

-------- G , ( a₂

x GFE J ^{1 2}

1 d ² G 1 ( a ₂ — a 1 ) x GF    dx x

• -4 Z — d . Z , — V ( a j) + EI

P to ² I G ₍₀₎L_ d ² G 2(0) x GFE ^{J J} x GF dxx

• -L ( Z + d 2 Z , — V ( a 2 )). I EI

Введя обозначения

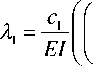
Р ® ² 1 G ₍°)__L d 2 G 1 (°) 1

X GFE )      / GF dx ² ,

Л = c^- 1 EI U

—

p® ² V ( -------- G ₂ ( a, XGFE J ^{2 1}

— a 2) —

1 d ² G ₂ ( a ₁ — a ₂ ) X GF     dx ²      .

Л = с^ I i — _p® _ I g ( a — a ) ^d G ¹⁽ a² a ¹) EI Ц x GFE J          X GF dx ²

Л₄ = c

⁴ EI

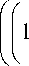
Р ® ² 1 _{G (}°)__L d² G 2 (°) 1

XGFE J A   XGF dx2 , преобразовав, перепишем (16) в виде

'( Л + Л ₂ ) Z + ( Л ₂ d ₂ — ^ d ₁ ) Z _v — (1 + Л )V ( a ₁ ) — X ₂V ( a ₂ ) = °, ^Л , + Л 4 ) Z + ( Л d 2 — Л d 1 ) Z _v — Л У ( a 1 ) — (1 + Л 4 ) V ( a 2 ) = °.

Объединив первое и второе уравнения системы (3) с системой (17), получим однородную систему линейных алгебраических уравнений относительно Z , Z ^ , V ( a ₁ ), V ( a ₂ ).

( - m ® ² + c₁ + c ₂ ) Z — ( с ₁ d ₁ + c ₂ d ₂ ) Z ^ — c₁V ( a ₁ ) — c ₂ V ( a ₂ ) = °,

- ( c ₁ d ₁ + c ₂ d ₂ ) Z — ( I ® ² — c ₁ d ₁ ² — c ₂ d ₂ ² ) Z _v + c ₁ d ₁ V ( a ₁ ) + c ₂ d ₂ V ( a ₂ ) = °, ( Л + Л ₂ ) Z + ( Л ₂ d ₂ — X ₁d ₁ ) Z _v — (1 + Л ) V ( a ₁ ) — Л ₂ V ( a ₂ ) = °,

( Л 3 + Л ₄) Z + ( Л ₄ d ₂ — Л 3 d ₁ ) Z _v — Л 3 V ( a ₁ ) — (1 + Л ₄ ) V ( a ₂ ) = °.

Однородная система алгебраических уравнений (18) имеет ненулевые решения, если ее определитель равен нулю. Приравняв определитель системы (18) к нулю, получим уравнение для нахождения собственных частот

	( — m ® 2 + c 1 + c )	— ( с1 d 1 + c 2 d 2 )	— c 1	— c 2
det	— ( c 1 d 1 + c 2 d 2 )	( — I ^ ® 2 + c 1 d 1 2 + c 2 d 2 2 )	c 1 d 1	c 2 d 2	= °. (19)
	( Л + Л 2 )	( Л 2 d 2 — Л d 1 )	— (1 + ^ 1 )	— 2 2 V ( a 2 )
	_ ( Л + Л 4 )	( Л 4 d 2 — Л 3 d 1 )	— Л 3	(1 + Л 4 ) _

Заключение

Обосновано построение частотного уравнения (19) для балки Тимошенко с прикрепленным с помощью двух пружин твердым телом с двумя степенями свободы. В целом статья является продолжением исследований, приведенных в [1].