Четырехволновое взаимодействие в многомодовом волноводе с керровской нелинейностью в схеме с попутными волнами накачки

Для получения волны с обращенным волновым фронтом (ОВФ) при четырехволновом взаимодействии в волноводах в качестве основной рассматривается схема взаимодействия со встречными волнами накачки [1–8]. В этой схеме волна с обращенным волновым фронтом (объектная волна) распространяется навстречу сигнальной волне, наблюдается полное обращение волнового фронта. Еще одной схемой четырехволнового взаимодействия является схема с попутными волнами накачки, в которой объектная и сигнальная волны распространяются в одном направлении [8–12]. В такой схеме наблюдается обращение лишь поперечной составляющей волнового вектора сигнальной волны.

Если качество обращения волнового фронта при четырехволновом взаимодействии в схеме с попутными волнами накачки в пространственно не ограниченных в поперечном направлении средах с различным типами нелинейности изучено достаточно подробно [8; 13–14], то аналогичные

работы по изучении четырехволнового взаимодействия в многомодовых волноводах отсутствуют.

В настоящей работе с использованием метода функции размытия точки (ФРТ) исследуется качество обращения волнового фронта четырехволновым преобразователем излучения в многомодовом волноводе с керровской нелинейностью в схеме с попутными волнами накачки.

1. Функция размытия точки четырехволнового преобразователя в волноводе

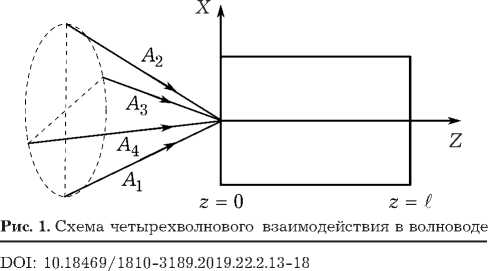
Рассмотрим вырожденное четырехволновое взаимодействие с попутными волнами накачки в волноводе с керровской нелинейностью, расположенном между плоскостями z = g и z = / . На волновод падают две волны накачки с комплексными амплитудами A ₁ и A ₂ и сигнальная волна с комплексной амплитудой A ₃ . В результате вырожденного четырехволнового взаимодействия (to + to - to = to) генерируется объектная волна A 4 (рис. 1). Исходное уравнение, описывающее такое взаимодействие, есть [8]

V² + к 2 г + 12=- Z ^{| 3 )} A ³ c ²

A = 0.

⁴                  | 3 )

Здесь A = £ Aj + к.c.; x   — нелинейная воспри- j=1

, 2 ^to 2 имчивость третьего порядка; k g = ——, s c ²

электрическая проницаемость.

–

ди-

Разложим взаимодействующие волны по мо-

дам волновода

N

A j = E a jn ( z ) f n ( x , z ), j = 1,4.                    (2)

n = 0

Здесь f n ( x , z ) = f_n ( x )exp { - i P n z } — n -я мода волновода, при отсутствии в нем керровской нелинейности; P _n — постоянная распространения n -й моды; a_jn ( z ) – коэффициенты в разложении амплитуд волн по модам волновода; N – число

отсечки.

При рассмотрении четырехволнового взаимодействия используем следующие приближения:

• 1)    интенсивность волн накачки намного больше интенсивностей сигнальной и объектной волн;

• 2)    коэффициент преобразования маленький;

• 3)    изменением показателя преломления за счет эффектов самовоздействия волн накачки можно пренебречь.

С учетом сделанных приближений из волнового уравнения (1) получим систему уравнений, описывающих изменение вдоль оси Z коэффициентов в разложении взаимодействующих волн

по модам волновода

da da da in = о, , zm = о,. 3s_ = о dz dz dz

da _{4 r} dz

NNN

= i в E , ^^ E <   ^a 1 n ^a 2 m a 3 s ^Y nmsr ^{x r} n = 0 m = 0 s = 0

a s 0 = f s ^{( x} 0 ).                                              ⁽⁷⁾

С учетом (6) и (7) выражение для ФРТ четырехволнового преобразователя излучения в волноводе есть

N f ( x )

Г( x, x 0) = igl^ -r— x r=0 P r

NNN xZZZan0am0fs(x0)Ynmsr x             (8)

n = 0 m = 0 s = 0

x exp j - i ^{A nmsr l} L sin c ^{A nmsr l} .

I 22

Если волны накачки одномодовые ( A i = a n 0 f_n , A 2 = a_m 0 f_m ), то выражение для ФРТ упрощается:

^Г nm ^{( x} , ^x 0 ) = ig ^l a n 0 a m 0 ^x

N /  N xE fr?-2 E fs(x0)Ynmsr x                    (9)

r = 0 ^{P r} s = 0

x exp /- i ^ nmsr l 1 sin c ^ nmsl i .

I 22

Формально выражения для ФРТ четырехволновых преобразователей в схемах с попутными и встречными волнами накачки совпадают [8; 15], меняется лишь выражение для волновой расстройки, и, как следствие, меняются моды, участвующие в формировании ФРТ.

^x exp { — i A nmsr ^z } .

x *      *

Здесь Y nmsr = J f n ( x ) f m ( x ) f s ( x ) f r ( x ) dx

-TO

2. Четырехволновой преобразователь излучения в параболическом волноводе

инте-

Рассмотрим двумерный параболический волно-

грал перекрытия; ^A nmsr = P n + P m ^{- P} s ^{- P} r ^-

вод с диэлектрической проницаемостью s ( x ) =

„ ^12л® ² „( 3 )

волновая расстройка; g = 2— X .

С учетом граничных условий a3s(z = 0) = as0; a4r(z = 0) = 0                        (5)

= S i 1 - 2 s2 ( xjx q ) ² .

Модами такого волновода

являются функции Гаусса – Эрмита [16]

из (3)–(4) выражение для коэффициентов разложения объектной волны по модам волновода

f n ( x ) = ⁴Z² , 1

’ ⁿ ^2 ⁿn ! ® 0

H n II exp ( ® 0 J

( 2A x — 2

I ® 0 J

есть gNNN a4r(z = l) = i p ^^ ^^ E < an0am0 as0Ynmsr x

^Prn = 0 m = 0 s = 0                          (6)

x exp L i ^{A nmsr l} I sin c ^{A nmsr l} ,

1       22

где a n 0 = ^a 1 n ^{( z} = ⁰⁾; a m 0 = a 2 m ^{( z} = ⁰⁾

Если сигнальной волной является волна от то-

ка; ® 0 =

Здесь H_n

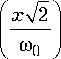
функция Эрмита n -го поряд-

2xq k у/ 2s2

Для приосевых мод ( 2^2 s2 / x q ( n + 1/2 ) <<

постоянная распространения есть

P n - k -

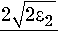
xq

. 1)

n +    .

2J

чечного источника, расположенного на перед ней грани волновода (Аз(x, z = 0) = 5(x - x0)), то

С учетом (11) выражение для волновой расстройки перепишется следующим образом:

^A nmsr

—

xq

[ n + m

— s — r ] .

В длинных волноводах ( A _nmsr t >> 1 ) условие фазового синхронизма определяет модовый состав объектной волны. Вид ФРТ, расположенной в центре поля зрения ( — 0 = 0 ) , и одномодовых

волн накачки с четными номерами мод опреде ляют моды с номерами r = 0, m, n, m + n:

ig t a^namn 2 ^f — 2

ГЦ (x) =   , n0 m0    exP k ®o    V п ( ю2 J

) V                       I ГГл/9 I , .

Y nnmm

I         = Hn I      I H m ^{(0) +}

V2 ^{n +} m m ! n ! L    I ^to 0 )

fI

+ Hm I      I Hn (0) +

,   ^Y0 nmm + n Г rr /n\ , rr I ^{— 21} I

+ /       ^=LHn+m (0) + Hn+m II Г .

V2 n ⁺ m m ! n !                    I ® 0 )JJ

Для одномодовых волн накачки с нечетными номерами мод вид ФРТ определяют моды с номерами r = 0, m + n :

Г⁽²⁾ (ж) = nm ^{( —} )

ig ^ a n 0 a m 0 k to o

^Y 0 nmm + n _x V 2 ^{n +} m m ! n !

2I

2 f — ² Irw : - exp   L H

V п ( to0 ) L

n+m (0) + Hn+m I

l to0

.

Для одномодовых волн накачки с номерами мод различной четности ФРТ отсутствует .

По сравнению с четырехволновым преобразователем излучения в волноводе в схеме со встречными волнами накачки число мод волновода, участвующих в формировании ФРТ четырехволнового преобразователя излучения в схеме с попутными волнами накачки, резко уменьшается.

Наряду с условием фазового синхронизма существенную роль на вид ФРТ оказывает интеграл перекрытия. Подробный анализ интеграла перекрытия для мод параболического волновода приведен в работе [15].

Будем считать, что волны накачки, падающие на волновод, плоские:

A 1 ( — , z = 0) = exp(— ik— sin 9 1 ),

A 2 (— , z = 0) = exp(— ik— sin 9 2 ).

Здесь 9 12 — углы между оптической осью волновода и направлением распространения волн накачки.

Для волн накачки, падающих на переднюю грань волновода под одинаковыми малыми угла-

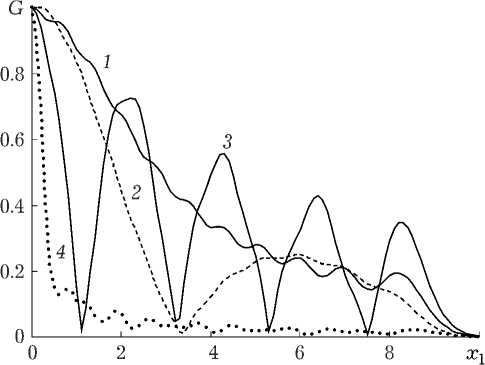
Рис. 2. Зависимость модуля ФРТ от нормированной поперечной координаты при k © о = 40, 9 = 0,1 ° ( 1 ), 1 ° (2 ), 3 ° ( 3 ) для встречной геометрии взаимодействия (4)

ми ( 9 = 9 1 =—9 2 , sin 9 12 =9 12 ) , выражения для коэффициентов в разложении волн накачки по

модам волновода имеют вид

_ 74П    2 4 i n

a1 n =         1

to0    1 ,----------- п 41^2 nn! too

f x exp

k ² 9 ² to ² ₀

x

H n

k 9to0

74П  24(—i)m a 2 m =--i-—-- to0    1 /----------- п 4 д/2 nm! to0

x

exp

—

k ² 9 ² to ² ₀

H m

x

k 9 to0

С учетом (15) для длинного волновода выражение для ФРТ примет вид r (1), x i 8 gt         —

Г (——) = —— e—p 2- x

k to0       4 to0

N 1 N 1 N 1

x^E

r = 0 n = 0 m = 0

nm i ( i) Y nmrn+m—r

2 ^{2( n + m —} r ) n ! m ! ( n + m ) !

x e—p

x Hm

l

22  2

k sinOtog

2I )

f k sin 9 to I

H„ ---1=—0 x

n l   V2   )

k sin 9to 0 1

^2   ) H n + m — r

(0) Hr

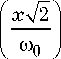
Здесь N ₁ – число мод волновода, учитываемых

при расчете ФРТ.

3. Обсуждение результатов

На рис. 2 приведены нормированные на максимальное значение (Г т)_ах ) характерные графики

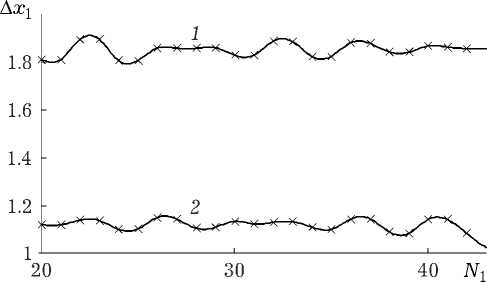
Рис. 3. Зависимости полуширины центрального максимума ФРТ от количества мод волновода, учитываемых при расчете ФРТ, при к Ш о = 40, 0 = 1 ° ( 1 ), 2 ° (2 )

зависимостей модуля ФРТ

( G = |г ⁽¹⁾ ( x )|/ r m)ax )

от нормированной поперечной координаты (Xi = = xV2/too) при различных углах падения волн на- качки на переднюю грань волновода. При расче- те графиков считалось, что количество приосе-вых мод, используемых при нахождении ФРТ, определяется из условия N = ^0,1 (к too )2 / 4 J. Для сравнения на рис. 2 (кривая 4) приведен график зависимости модуля ФРТ от поперечной координаты для четырехволнового преобразова- теля в схеме со встречными волнами накачки. Полуширина модуля ФРТ такого преобразователя (Ax), определяемая из решения уравнения

G (x = Ax) = 0,5,

не меняется при изменении угла падения волн накачки на грани волновода .

При k Ш о = 40 и угле падения волн накачки 0 ^ 0 полуширина модуля ФРТ четырехволнового преобразователя в схеме с попутными волнами накачки полностью определяется параметром волновода to 0 (A x — 2, 07© 0 ) и более чем на порядок превышает полуширину модуля ФРТ четырехволнового преобразователя в схеме со встречными волнами накачки (A x — 0,19© 0 ).

Увеличение угла падения волн накачки приводит к возникновению «тонкой» структуры ФРТ, т. е. появляются боковые максимумы, количество и величина которых возрастает. При этом расстояние между побочными максимумами уменьшается, а ширина огибающей модуля ФРТ увеличивается.

При больших углах падения (1° < 0 < 5°), как следует из анализа коэффициентов в разложении волн накачки по модам волновода, основная энергия волн накачки распределена на высоких модах волновода. Это приводит к росту коэффициентов, соответствующих высоким модам, в разложении амплитуды объектной волны по модам волновода и как следствие – увеличению энергии, сосредоточенной в побочных максимумах ФРТ. Количество побочных максимумов возрастает с увеличением параметра кШ0.

Сходное поведение ФРТ в зависимости от угла между волнами накачки наблюдается и для четырехволнового преобразователя c попутными волнами накачки в пространственно не ограниченной по поперечным размерам среде с керровской нелинейностью [8].

На рис. 3 для двух углов падения волн накачки приведены зависимости нормированной полуширины центрального максимума (A x i = A x V2 / © 0 ) от количества мод волновода, учитываемых при расчете ФРТ . Так, для волновода с параметром к © 0 = 40 увеличение числа мод от 30 до 40 при угле падения волн накачки 0 = 1 ° изменяет полуширину центрального максимума на 2,7 %, а при угле падения 0 = 2 ° — 3,3 %. Количество мод волновода, учитываемое при расчете ФРТ, при котором полуширина центрального максимума этой функции с погрешностью ±3 % перестает меняться с увеличением количества мод, меньше, чем число приосевых мод. Таким образом, учет приосевых мод волновода полностью определяет вид и полуширину центрального максимума ФРТ четырехволнового преобразователя в схеме с попутными волнами накачки.

Заметим, что характер поведения ФРТ четырехволнового преобразователя не изменится, если в качестве волн накачки используются не плоские волны, а волны с гауссовым профилем.

Заключение